基于改進模糊控制算法的分數階控制器設計

李莉，陳曉靜，徐智超

(大連科技學院電氣工程學院，遼寧大連116052)

0 前言

在控制領域中，線性最佳控制的分數階控制器在各個行業(yè)應用廣泛，其設計可按照被控制對象模型展開，操作簡捷，實用性強。目前，分數階控制器種類繁多，如余艷偉和徐鵬飛設計的基于內模控制的分數階控制器，該控制器參數按照最高靈敏度數值設定，選擇參數具有盲目性，其控制準確度較差；魏立新等設計了基于粒子群算法的液壓APC系統分數階PID控制器，該控制器主要應用在高冷液壓系統，應用范圍小，并且使用粒子群算法，迭代次數多，運算用時長，導致控制效果較差。針對目前控制器存在的一系列問題，本文作者基于改進模糊控制算法設計分數階控制器，采用區(qū)間二型模糊邏輯系統結構與改進的徑向基函數(Radial Basis Function，RBF)模糊神經網絡算法實現控制。區(qū)間二型模糊邏輯系統可對數據集合解模糊化，實現降階處理。改進的RBF模糊神經網絡算法可將前件網絡由三層增加至四層，具有減少模糊規(guī)則層節(jié)點數量、降低冗余模糊規(guī)則、提升學習速度等優(yōu)勢。使用區(qū)間二型模糊邏輯系統結構與改進的RBF模糊神經網絡算法，可實現控制器多方面需求，實際應用意義較大。

1 改進模糊控制算法的分數階控制器設計

1.1 區(qū)間二型模糊邏輯系統結構

與一型模糊邏輯系統相比，二型模糊邏輯系統具備降階流程，可將二型模糊集合轉化為一型模糊集合，對該集合實施解模糊化，實現二型模糊邏輯系統的降階。圖1所示為二型模糊邏輯系統結構。

圖1 二型模糊邏輯系統結構

根據圖1所示的二型模糊邏輯系統結構，利用KM(Krasnoselskii-Mann)降階算法對區(qū)間二型模糊集合進行降階處理。假設實數區(qū)間[,]，則、端點可由以下公式表示：

(1)

(2)

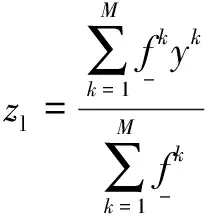
(3)

(4)

降階后的區(qū)間二型模糊集合為

(5)

1.2 分數階區(qū)間二型模糊邏輯系統

根據公式(5)得到的降階后的區(qū)間二型模糊集合，利用分數階算子構建分數階區(qū)間二型模糊邏輯系統。Riemann-Liouville可定義分數階微積分，由公式(6)表示：

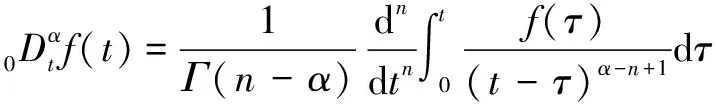
(6)

其中：(·)為伽馬函數；為整數，≥>-1。

用Grunwald-Letnikov定義分數階微積分流程如下：

(7)

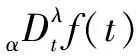
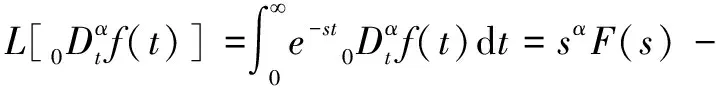
(8)

其中：-為收斂因子。

設置初值為0，則有：

(9)

分數階PID控制器時域可由公式(10)計算：

(10)

其中:()為時域函數輸出量；()為時域函數輸入量；為比例增益；為積分增益；為微分增益；分數階PID的傳遞函數經過拉普拉斯轉換可由公式(11)表示：

()=++

(11)

其中:>0，>0。

1.3 改進的RBF模糊神經網絡結構與算法

在設計區(qū)間二型模糊邏輯系統的基礎上，為避免模糊規(guī)則層節(jié)點數量較多導致其控制精度和控制靈敏度較低的問題，使用改進的RBF模糊神經網絡算法對其進行優(yōu)化設計。具體過程：將RBF模糊神經網絡的前件網絡由三層變更為四層，后件網絡中使用權值的二階學習，以減少模糊規(guī)則層節(jié)點數量，提升權值作用。改進后的RBF模糊神經網結構如圖2所示。

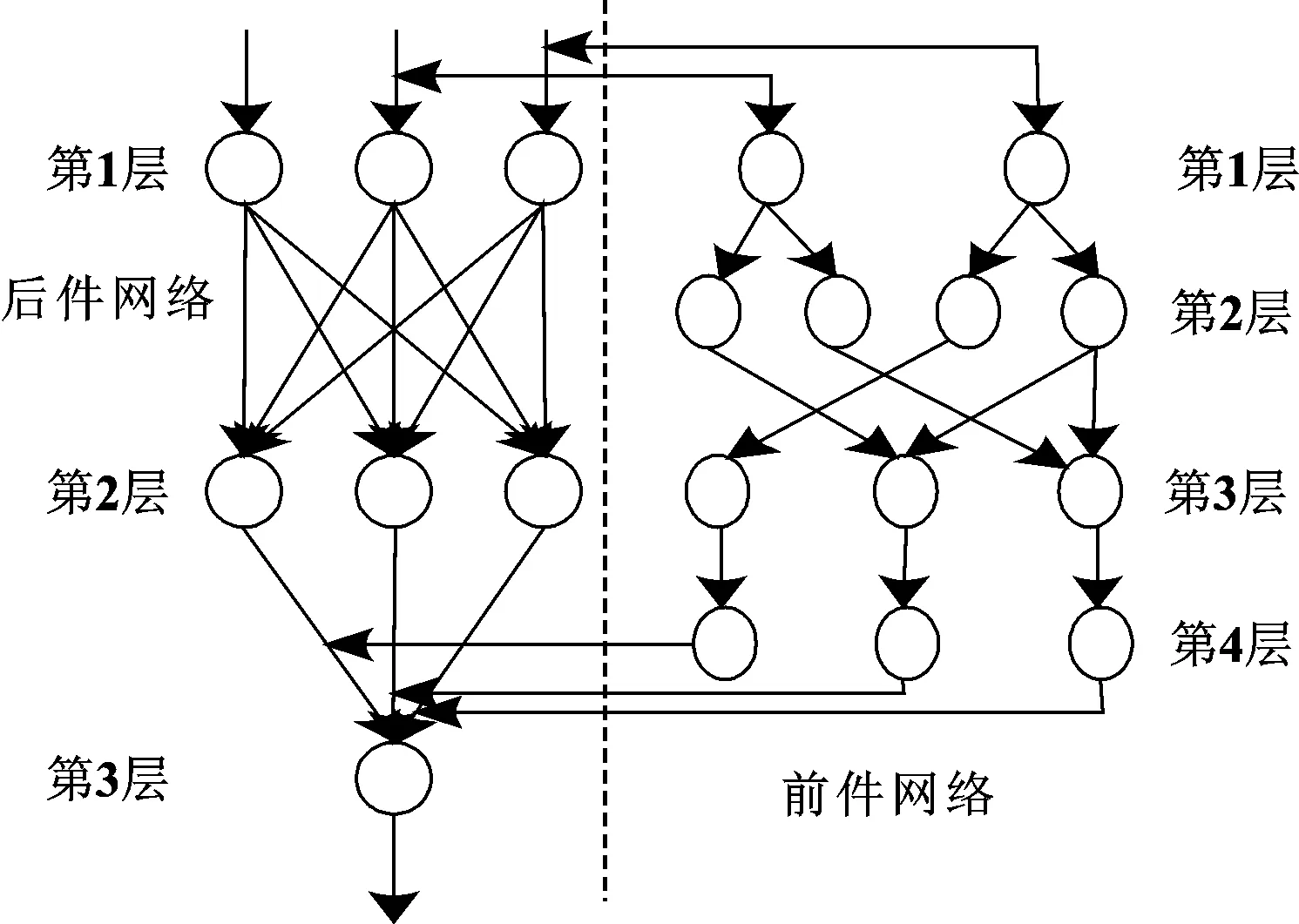
圖2 改進后的RBF模糊神經網結構

根據圖2所示的改進后的RBF模糊神經網絡結構，分別從前件網絡、后件網絡、修正參數3個方面優(yōu)化分數階控制器。

1.3.1 前件網絡

(1)輸入層。用連接輸入層每個結點之間和輸入向量的分量，可傳輸輸入值=[,,…,]至下一層，輸入變量數量即為結點數量=。

(12)

其中:=1,2,…,。

(13)

(14)

其中：表示隸屬函數中心;表示隸屬函數寬度，其結點總數為

(15)

(3)模糊推理層可計算各個規(guī)則的適合度，一個模糊規(guī)則表示一個結點，可用該規(guī)則匹配模糊規(guī)則前件，其公式如下：

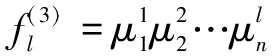
(16)

1.3.2 后件網絡

(1)輸入層可將輸入變量傳輸至第二層，其公式為

=

(17)

(2)中間層通過計算任一規(guī)則后件，在個結點中，每條規(guī)則都由一個結點表示，則有：

(18)

其中:=1,2,…,。

(3)輸出層可計算二型模糊邏輯系統的輸出，其公式為

(19)

1.3.3 修正參數

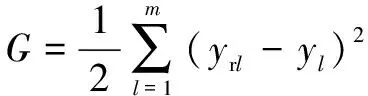
(20)

(21)

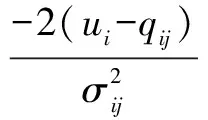
(22)

(23)

(24)

(25)

其中:=1,2,…,;=1,2，…，;=1,2,…,；表示學習率，>0。

為進一步提升控制器的靈敏度，將權值的平方運用于后件網絡多項式運算中，則：

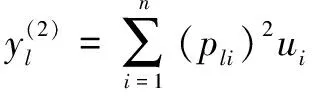
(26)

其中:=1,2,…,。

那么修正后的如下：

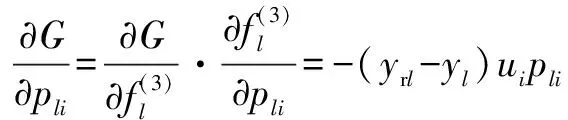
(27)

至此,實現基于改進RBF模糊神經網絡算法的分數階控制器設計。

2 實驗分析

為驗證所設計的控制器的控制效果，選取文獻[4]設計的基于內模控制的分數階控制器、文獻[5]設計的基于粒子群算法的液壓APC系統分數階PID控制器為對比控制器，利用MATLAB軟件分別建立3種控制器的仿真環(huán)境，并設置溫度為26 ℃，控制誤差±0.5 ℃。分別使用3種控制器對溫度進行控制，其階躍響應曲線如圖3所示。

圖3 3種控制器階躍響應曲線

由圖3可知：文中控制器階躍響應曲線較平滑，可穩(wěn)定控制溫度在26.01 ℃左右，與所控溫度目標相差僅為0.01 ℃，原因是本文作者在設計控制器過程中選擇恰當的切換點數值作為左右兩端端點值，利用簡化降階算法減少尋找切換點迭代次數，提高了控制的穩(wěn)定性；而文獻[4]控制器曲線為波浪狀，控制溫度時高時低，控制穩(wěn)定性較差；文獻[5]控制曲線呈現下降趨勢，在=30 s時，溫度較準確，當時間超過30 s后，溫度明顯低于設置溫度，溫度控制不穩(wěn)定。

控制器性能的優(yōu)良可由其控制指標呈現，其指標包括超調量、余差、調節(jié)時間等。對比3種控制器控制指標，結果如表1所示。

表1 控制指標對比

由表1可知：文中控制器超調量最小，為1.3%，其溫度余差與文獻[5]的余差都為0，但文中控制器超調量與調節(jié)時間都較小。由此可知，文中控制器用時短、偏差小、控制能力強。

對比3種控制器不同時間的溫度控制相對偏差情況，結果由圖4所示。可知：當=0～3.8 s時，文中控制器控制的溫度偏差高于文獻[4]與文獻[5]控制器的溫度偏差；當>3.8 s后，文中控制器控制的溫度偏差小于文獻[4]與文獻[5]控制器所控制的溫度偏差，文中控制器溫度偏差為-0.1～0.4 ℃，文獻[4]控制器溫度偏差為-0.17～0.82 ℃，文獻[5]控制器溫度偏差為-0.18～0.78 ℃，可見文中控制器控制溫度偏差較小，控制器響應性高。

圖4 溫度控制相對偏差曲線 圖5 3種控制器魯棒性能曲線

為驗證所設計的控制器魯棒性，統計3個控制器控制下不同時間的幅值，結果如圖5所示。可知:隨著時間的增加，3種控制器幅值主要呈上升趨勢，但文中控制器幅值上升速度最快，且達到最高幅值后始終處于穩(wěn)定狀態(tài)，文獻[4]、文獻[5]控制器幅值上升速度小于文中控制器，且波動顯著。由此可知，文中控制器控制穩(wěn)定性好、魯棒性強。

控制器靈敏度與互補靈敏度影響該控制器整體性能，3種控制器靈敏度與互補靈敏度曲線由圖6所示。

圖6 3種控制器靈敏度與互補靈敏度曲線

由圖6可知：控制器的靈敏度隨著頻率的增加而增加；當頻率為1×10～1 rad/s時，3種控制器靈敏度均明顯上升，文中控制器靈敏度上升幅度明顯高于文獻[4]與文獻[5]控制器；當頻率為1～1×10rad/s時，文中控制器靈敏度保持0不變，而文獻[4]與文獻[5]控制器靈敏度均低于文中控制器靈敏度；控制器的互補靈敏度隨著頻率的增加而降低；當頻率為1×10～1 rad/s時，文中控制器互補靈敏度保持0不變，并且高于文獻[4]與文獻[5]控制器互補靈敏度；當頻率為1～1×10rad/s時，3種控制器互補靈敏度呈下降趨勢。因此，文中控制器靈敏度高于對比系統靈敏度，實際使用性能較強。

為進一步驗證所設計的控制器的實際使用性能，分別對比3種控制器的時域響應情況，結果如圖7所示。

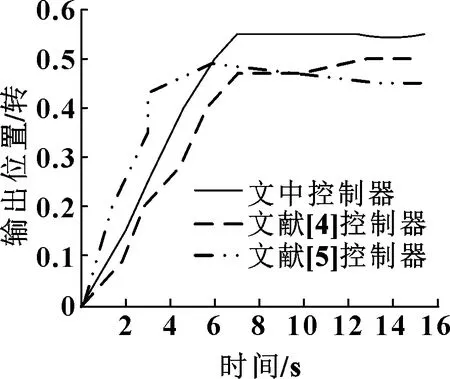
圖7 3種控制器時域響應曲線

由圖7可知：控制器輸出位置隨著時間的增加而增加，當到達一定時間后，輸出位置上下浮動較小；文獻[5]控制器時域響應曲線在=4.7 s之前，輸出位置高于文中系統與文獻[4]控制器，當>4.7 s后，其時域響應曲線呈下降趨勢，可見其時域響應性能差，參數跟蹤能力低；文獻[4]控制器整體輸出位置均低于文中控制器與文獻[5]控制器，時域響應能力低；而文中控制器時域曲線上升速度快，當時間約大于6.3 s時，其輸出位置遠高于文獻[4]與文獻[5]控制器，時域響應與參數跟蹤能力較好。

3 結論

本文作者采用分數階區(qū)間二型模糊邏輯系統和改進的RBF模糊神經網絡算法設計分數階控制器。經過實驗驗證，該控制器控制溫度精確度較高，可達到設定控制需求；較對比控制器，其靈敏度與互補靈敏度高、魯棒性能強、響應速率高。該控制器在實際應用中具有較高的控制效果，可進一步改進，以達到更好的控制效果。