具有符號式位置正解的2T1R并聯機構的運動學分析與尺度綜合

陳亞,彭紅梅,劉艷梨,吳洪濤

(1.江蘇安全技術職業學院機械工程系，江蘇徐州 221011；2.南京航空航天大學機電學院,江蘇南京 210016)

0 前言

少自由度并聯機構因具有結構、控制簡單,制造成本低,精度高等優點而備受學者關注。其中研究較多的是三維純平移和三維純轉動并聯機構，對二維移動一維轉動(2T1R)空間并聯機構的研究較少。2T1R空間并聯機構可通過調整姿態角快速地完成拾取物品操作，具有很好的運動靈活性。2T1R空間并聯機構在醫療器械、物料分揀等應用領域具有較好的應用前景。

關于2T1R并聯機構的研究，吉昊等人提出一種可應用于腳踝按摩儀領域的2T1R并聯機構，根據計算得到的方位特征集、自由度、耦合度驗證運動特性，通過序單開鏈的運動學建模方法計算得到位置正解和逆解的解析式，仿真分析其工作空間和轉動能力、奇異性等特性。沈惠平等針對并聯機構誤差分析、動力學分析、運動軌跡規劃分析復雜的問題，提出2種具有解析式位置正解且運動解耦的2T1R并聯機構，分別對這2種機構建模進行運動學和性能分析，對比分析優選出最佳性能的機型。張彥斌等設計了一種弱耦合空間三自由度并聯機構,采用方位特征集分析機構的運動特性，同時建立機構的正逆解方程，在此基礎上分析機構的奇異性，并分類分析研究。鄧嘉鳴等基于方位特征方程的并聯機構設計理論與方法，提出一種無寄生運動非對稱空間2T1R并聯機構，對機構的拓撲特性進行了分析，基于序單開鏈法的運動學原理得到機構正逆解，同時研究了機構的工作空間、奇異位形、轉動能力等工作性能。黃勇剛和黃茂林根據螺旋理論與集合論原理,基于動平臺所受約束與支鏈約束之間的關系,分析平面機構無過約束構型條件，綜合出一批無過約束平面2T1R并聯機構。張彥斌等設計一種完全各向同性的三自由度空間并聯機構，通過調整支鏈的排列關系，演化出另外2種新型整周旋轉(360)的2T1R并聯機構，最后根據螺旋理論完成自由度分析以及求解出機構的運動學正逆解。劉偉和劉宏昭基于位移流形理論，綜合出具有2T1R與2R1T2種運動模式的并聯機構，通過螺旋理論研究不同運動模式下的自由度特征。鄒建星等設計一種兩平移一轉動(2TIR)并聯機構，對機構的拓撲性能進行分析，證明機構的運動性質，建立運動學方程推導得到位置逆解解析式，分析工作空間和轉動能力等性能指標。

本文作者利用方位特征方程(Position and Orientation Characteristics，POC)的并聯機構設計理論與方法，提出一種具有解析式位置正解且部分運動解耦的2T1R并聯機構。分析機構的主要拓撲特性,由于耦合度為零，推導出運動位置正解與逆解的解析式；研究了機構的工作空間形狀和大小及奇異性存在條件；以給定的工作空間指標作為優化目標函數的約束條件，建立工作空間最小化的優化目標函數，優化得到一組最佳參數解，為后期的軌跡規劃、動力學分析奠定理論基礎。

1 并聯機構設計與拓撲結構分析

1.1 機構設計及坐標系的建立

如圖1所示為2T1R機構結構簡圖,支鏈1由1個平面五桿閉回路和1個轉動副串聯而成，、、軸線相互平行且垂直于，移動副、的移動方向一致，軸線與平行。支鏈2由一個平行四邊形機構和一個副、轉動副構成，其中，副與副互相平行。副的移動方向和移動副一致。圖2所示為2T1R并聯機構三維模型。

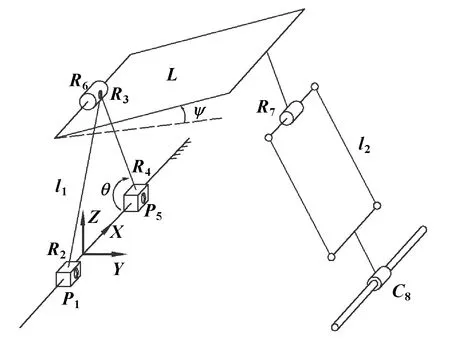
圖1 2T1R并聯機構結構簡圖

圖2 2T1R并聯機構三維模型

在靜平臺上建立坐標系{-}，其中軸與移動副所安裝的邊平行，與移動方向垂直。軸垂直于靜平臺，該機構以主動移動副的位置作為獨立的輸入參數，用(,,)表示，輸出參數為(,,)，即動平臺的位姿，具體參數如表1所示。

表1 參數描述

1.2 機構動平臺POC分析

并聯機構拓撲結構特性分析方法見文獻[13]，具體計算過程如下：

(1)首先選定動平臺上任意一點，作為動平臺上基準點。

(2)其次，需要得到每條支路的POC集，其中機構存在3條支路，第一條支路的POC集為

(1)

其中:，且移動副，移動方向與轉動副垂直。因此，

(2)

同理，第2條支路的POC集為

(3)

第3條支路的POC集為

(4)

其中，副可以衍生成副和副，因此，

(5)

(3)建立方位特征方程可得：

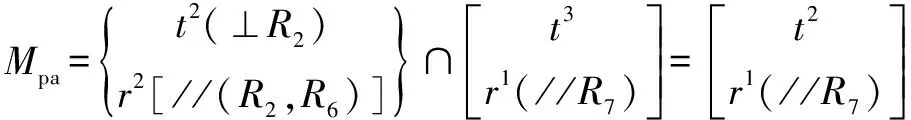
(6)

(4)需要得到每一條回路獨立位移方程數，該機構存在2條回路，確定第一個獨立回路的獨立位移方程數,由下式可得：

(7)

(8)

(5)確定第2個獨立回路的獨立位移方程數。

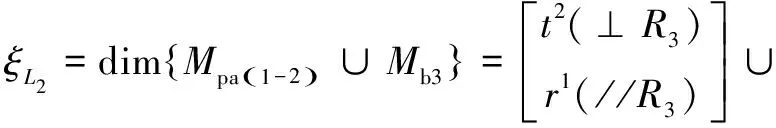
(9)

(6)確定機構的方位特征集。

(10)

(7)計算自由度，過程如下：

(11)

(8)根據上面的分析過程，=3，=5，計算約束度可得：

(12)

(9)基本運動鏈的耦合度計算如下：

(13)

綜上所述，計算得到運動鏈的耦合度為0，說明機構的運動學比較簡單，且機構的正解存在解析式，運動學與動力學可單獨求解，有利于機構的控制軌跡規劃。

2 機構的位置分析

2.1 機構位置正解分析

機構位置正解是指已知輸入位移(,,),得到機構動平臺的位置姿態(,,)。設置作為動平臺參考點，由于△為等腰三角形，根據結構參數和運動副分布，可得以下特征參數方程：

(14)

式(14)聯立得到的表達式：

(15)

根據坐標可得到在軸上的坐標：

=+sin

(16)

由于平行四邊行機構的桿長不變，存在以下等式關系：

(17)

因此，分離變量可得到參數的表達式

(18)

根據式(15)、式(18)即可解出姿態角參數和各2個,機構正解表達式簡單，機構的正解有4組。

2.2 機構位置逆解分析

位置逆解分析是指已知機構的結構參數和末端執行器的位姿，求解主動關節的位置，即已知(,,)，求解(,,)。根據上述正解分析過程等式(14)，可以得到機構的、逆解表達式：

(19)

(20)

通過等式(17)可推導出機構主動關節位置的表達式：

(21)

以上主動移動副機構存在4組位置逆解。

2.3 正逆解驗證

給定一組機構參數驗證運動學位置分析的準確性，選擇參數=0.5 m、=1 m、=1.5 m,根據MATLAB計算得到位置正解數值(見表2);根據公式(19)—式(21)，隨機代入數值得到機構位置逆解數值,結果如表3所示。

表2 機構的位置正解數值

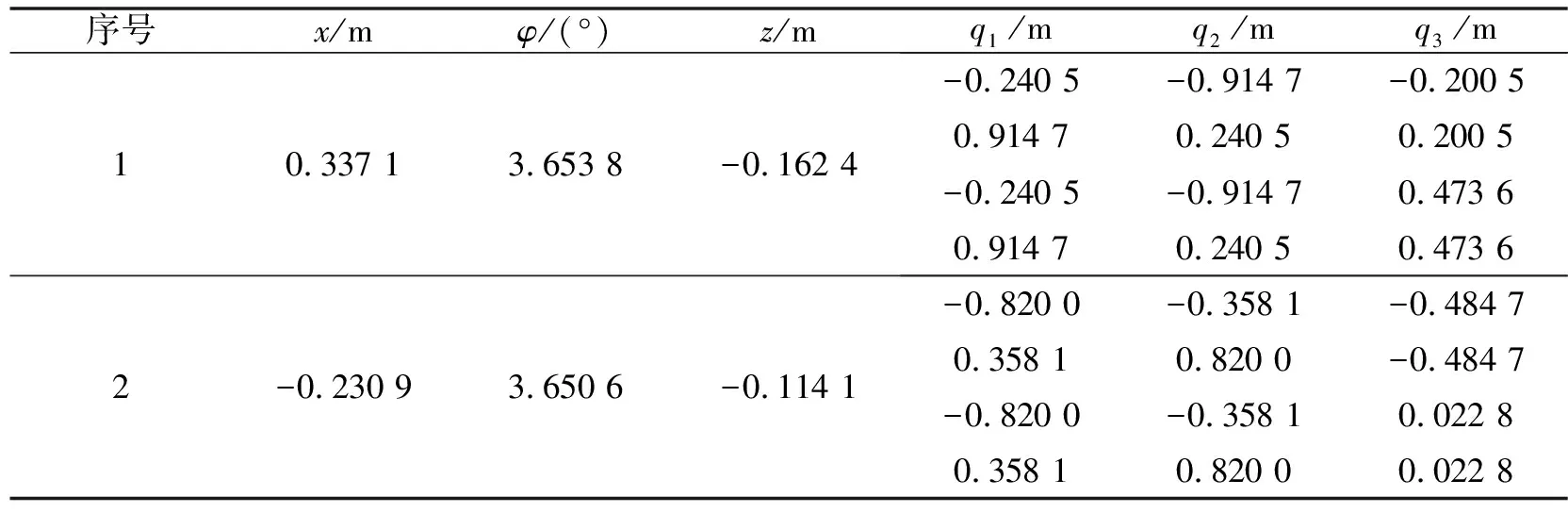
表3 機構的位置逆解數值

根據表2、表3中的數值解可以發現：位置正逆解能夠相互對應，驗證了分析得到的位置正逆解的可靠性。

3 奇異分析

3.1 機構雅克比矩陣

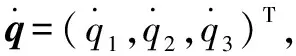
(22)

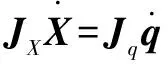
(23)

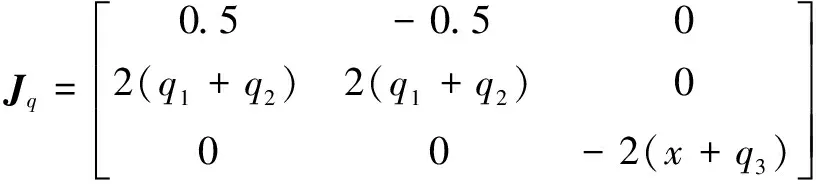
其中:為逆雅克比矩陣;為正雅克比矩陣。

若非奇異，則

(24)

若非奇異，則

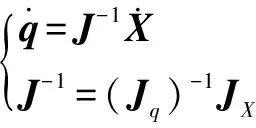
(25)

3.2 逆解奇異性分析

機構逆解奇異存在條件為det()=0且det()≠0，整理可得：det()=2(+)(-)，使得det()=0的條件是=-或=。

因此，存在以下2種情況：

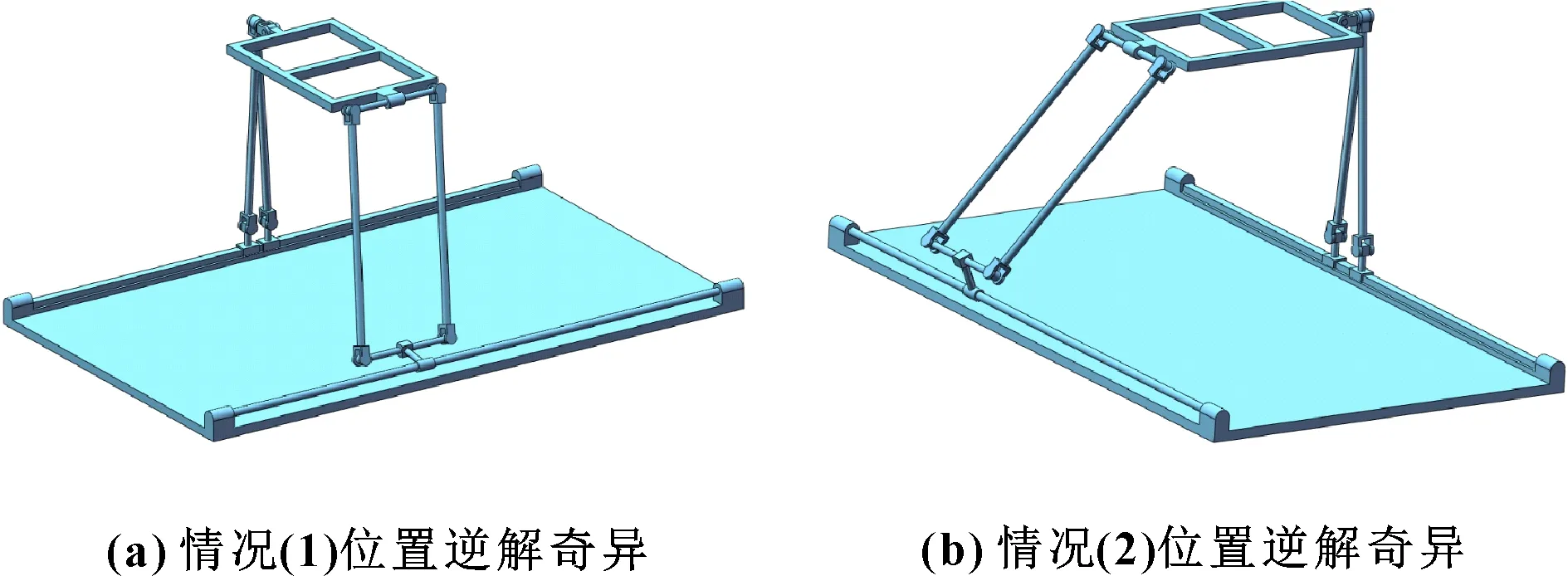
圖3 位置逆解奇異

3.3 正解奇異性分析

正解奇異情況具體如下：

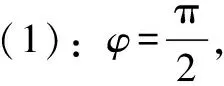
圖4 位置正解奇異

4 機構的工作空間分析

并聯機構的工作空間是指動平臺參考點所能夠達到的位置集合。針對工作空間采用極坐標搜索法實現工作空間圖形化分析。判斷是否是工作空間內點的條件是所有輸入位移(,,)是否滿足取值范圍要求，是則為工作空間內的點。以下圖形化分析均根據表4中的尺寸參數進行求解。

表4 機構的尺寸參數

由圖5可知：搜索得到的工作空間圖形狀為對稱的規則形狀，呈現對稱腰狀圖，工作空間邊界光滑飽滿、無空洞情況。

圖5 2T1R并聯機構工作空間

5 結構參數對工作空間的影響

參數大小選擇會直接影響到工作空間的大小。作為并聯機構重要性能指標，研究結構參數和工作空間大小的影響關系可用于指導并聯機構的應用設計。、、、對工作空間大小的影響關系如圖6所示。

圖6 參數對工作空間大小的影響關系

分析圖6可知：各參數對并聯機構工作空間的大小影響顯著，其中結構參數對工作空間影響呈線性相關，隨著的增加工作空間反而減少；參數對工作空間影響呈先增加后減小的趨勢，當∈[0.4,0.6]m，越大，工作空間體積越大，當∈[0.6,1]m，越大，工作空間越小；參數對工作空間大小的影響趨勢和參數基本一致，∈[0.5,0.8]m，越大，工作空間體積越大，∈[0.8,1.1]m，越大，工作空間體積越小；而參數增加有利于提高工作空間體積，隨著參數增加，工作空間體積越大。

6 機構給定工作空間優化

在某種工況下需要滿足特定的工作空間，即給定工作空間區域，尺寸參數越大，越有利于工作空間的增加，但是并非越大越好，因此，需要優化得到的是并聯機構工作空間且能包含給定工作空間的同時所對應的并聯機構的最優尺寸參數值最小。

6.1 優化模型的建立

給定一個工作空間形狀的操作區域，以原點為中心，給定正方體邊長為1 m，優化目標為所求工作空間體積最小，約束條件為工作空間包含此正方體。建立此優化目標的目標函數，是要找到合適的約束條件，在約束條件下，采用優化算法獲得最小的優化結果。

優化目標為包含此正方體，且可達工作空間體積最小。假定從原點出發，均勻發射出射線，射線集合為{},穿過的給定正方體集合為{}，在某一組參數下，工作空間的邊界和射線的交點集合為{}，當≥時，則為滿足包含要求。在滿足此約束的條件下，目標函數值等于根據蒙特卡羅法計算出這組參數的工作空間體積，若不滿足則取一個較大的數作為該組參數的目標函數值。

(26)

(27)

其中：為一較大的正數，設定為比目標函數值最大值大得多的數，取=100。

6.2 優化算法的選擇與優化結果

參數優化算法有很多，選擇天牛群優化(Beetle Swarm Optimization，BSO)算法進行目標函數的優化。天牛群優化算法是2017年發表的天牛須搜索算法的改進算法，是一種生物啟發式算法。表5列出了相應的算法參數。

表5 天牛群算法參數

經過迭代計算優化得到BSO算法最優參數值如表6所示，目標函數優化過程如圖7和圖8所示,優化在約80步時完成了迭代過程。

表6 天牛群優化算法結果

圖7 天牛群算法優化過程 圖8 變量隨代數變化影響曲線

圖9是相對應的優化工作空間圖，綠色為給定工作空間，紅色為優化參數下的可達工作空間(呈現為左右凹型的對稱空間)。由圖9可知:=±0.5 m的平面，=±0.5 m平面和給定工作空間完全重合，而可達工作空間在=±0.5 m和給定工作空間相切，故而目標優化完成，給定工作空間全部包含于可達工作空間，且呈現6個面全部重合的結果，得到了滿足給定的工作空間且使并聯機構的結構尺寸最小的最優解。

圖9 優化后的給定工作空間和可達工作空間三維圖

7 結論

(1)文中設計了一種有解析式位置正解、工作空間較大的空間2T1R并聯機構，分析了機構的拓撲特性，結果表明:機構的耦合度為0且具有運動解耦的特點。

(2)搜索得到的工作空間形狀為對稱的規則形狀，呈現對稱腰狀圖，工作空間邊界光滑飽滿、無空洞情況。

(3)根據優化后算例分析的工作空間圖表明：給定工作空間的6個面全部和可達工作空間相切或重合。優化得到滿足給定的工作空間且使實際工作空間最小的設計結構參數尺寸最優解，設計參數、、、、的最優解分別為0.3 m、0.501 1 m、0.952 2 m、1.002 1 m、1.195 1 m。