基于VMD與IFWA-SVM的滾動軸承故障診斷研究
張炎亮,毛賀年,趙華東
(1.鄭州大學管理工程學院,河南鄭州 450001;2.鄭州大學機械與動力工程學院,河南鄭州 450001)
0 前言
滾動軸承是機械設備的關鍵部件,如果它發生故障,將影響系統的正常運行甚至造成整個系統癱瘓。目前對故障診斷的研究主要集中在故障特征提取和分類識別兩方面。
許多學者采用經驗模態分解(Empirical Mode Decomposition,EMD)處理非平穩性信號,效果良好。但是,EMD存在模態分量混疊和端點發散現象,對信號采集頻率和噪聲較為敏感。針對EMD存在的缺陷,徐可等人提出一種自適應波形匹配的延拓方法改進EMD;何青等人加入白噪聲對原始信號進行了重構,提出集合經驗模態分解(Ensemble Empirical Mode Decomposition,EEMD),有效地提取到系統故障的非線性特征,然而白噪聲的加入降低了計算效率;郝勇等人提出變分模態分解(Variational Mode Decomposition,VMD),分析了不同品質的軸承信號,實現了對不同品質軸承的識別。以上研究多以單一特征值進行故障診斷,針對單一特征值進行多故障識別效率低下的問題,提出時域指標結合固有模態分量樣本熵(TDI-VMD-SE)的滾動軸承特征提取方法。
故障診斷的本質為故障模式的識別,在模式識別中,支持向量機(Support Vector Machine,SVM)建立在統計學習理論和結構風險最小化的基礎上,具有良好的推廣泛化能力。但SVM模型受核函數參數和懲罰因子影響較大,許多學者們利用遺傳算法、狼群優化算法、粒子群算法對SVM參數尋優,但以上算法對于高維復雜問題,易早熟收斂且耗時較長。煙花算法(Fireworks Algorithm,FWA)根據煙花適應度確定搜索范圍和搜索精度,合理分配搜索資源,具有良好的優化性能。隨著對煙花算法的深入研究,該算法已經得到廣泛應用和改進。ZHENG等使煙花之間進行有效交互,提出煙花算法的協作框架。LI等利用目標函數信息構造變異算子,提出引導煙花算法。目前煙花算法已經應用到路徑優化、多能源系統調度、太陽能電池參數辨別等優化問題,但將它應用到SVM參數優化的研究極少。針對煙花算法以輪盤賭的方式選擇子代,造成子代隨機性過大、算法收斂效率低的問題,本文作者應用一種改進選擇策略的煙花算法對SVM參數進行尋優,并應用于滾動軸承的故障診斷。
1 基于VMD的信號分解
VMD算法主要為變分問題構建和分解過程。VMD算法通過迭代搜索變分模型最優解,自適應地對模態分量的中心頻率和帶寬進行匹配,從而實現信號的頻域劃分和多個模態分量的分離。具體步驟如下:
(1)對各模態函數進行Hilbert變換,得到每個模態函數()的解析信號:
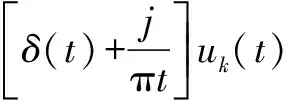
(1)
(2)對各模態解析信號估計的中心頻率進行指數修正,使模態函數的頻譜調制到相應的基頻帶上。
(3)計算解調信號梯度的平方L2范數,獲取各模態的估計帶寬,并要求其帶寬之和最小,即滿足:
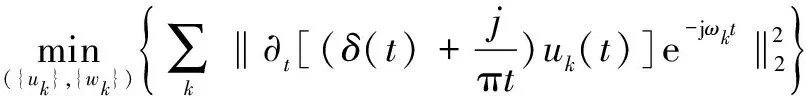
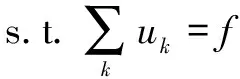
(2)
為便于求解,將上述約束變分問題轉化為非變分問題,引入二次懲罰因子及拉格朗日乘子(),擴展的拉格朗日表達式如下:
({},{},)=

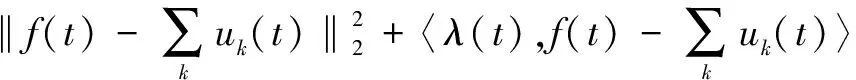
(3)
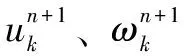
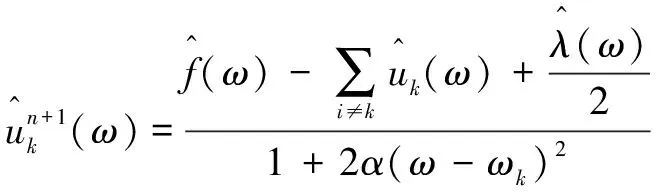
(4)
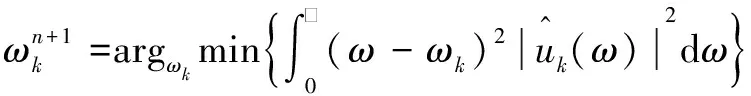
(5)
2 改進煙花算法優化支持向量機
2.1 煙花算法及選擇策略的改進
煙花算法通過模擬煙花爆炸,對煙花及火花不斷篩選,最終得到全局最優解。該算法基于免疫思想,根據種群的適應度進行分配搜索資源,未改進的煙花算法參考文獻[9]。為改善收斂速度和收斂精度,對選擇策略作如下改進:
將適應度進行歸一化處理:
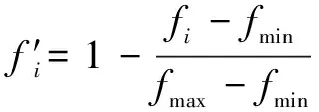
(6)
式中:′為歸一化后的轉義適應度。
在距離的計算公式中引入轉義適應度,分別計算轉義適應度為1和非1的距離′:
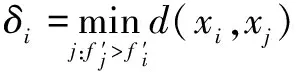
(7)
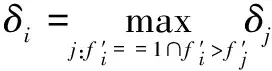
(8)
對′進行歸一化處理,即:
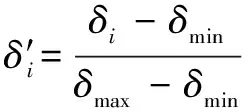
(9)
將轉義適應度′與歸一化距離′的乘積作為子代火花的選擇依據:
=′×′
(10)
按照數值從大到小的順序選取前-1個火花作為下一代煙花。為保證煙花算法的全局搜索能力,定義搜索區域最邊緣的一個火花,即與其他火花之間距離之和最大的火花作為探索火花,滿足下式:
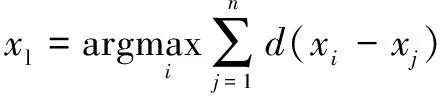
(11)
改進煙花算法具體步驟如下:
(1)設置可行域(懲罰因子、徑向基核參數的范圍),并在可行域內隨機生成個煙花;
(2)計算生成煙花的適應度,并以適應度為依據,執行爆炸算子操作生成火花;
(3)隨機選取個火花,進行高斯變異;
(4)判斷所有火花是否超出可行域范圍,并對超出邊界的火花執行映射規則;
(5)執行式(6)—(11)的計算,得到下一代煙花群體,判斷是否達到函數最大的評估次數,若滿足,計算終止;否則繼續循環。
2.2 改進煙花算法優化支持向量機
針對支持向量機識別準確率受核函數參數及懲罰參數影響較大,本文作者采用IFWA優化核函數參數及懲罰參數。優化流程如圖1所示,具體過程如下:
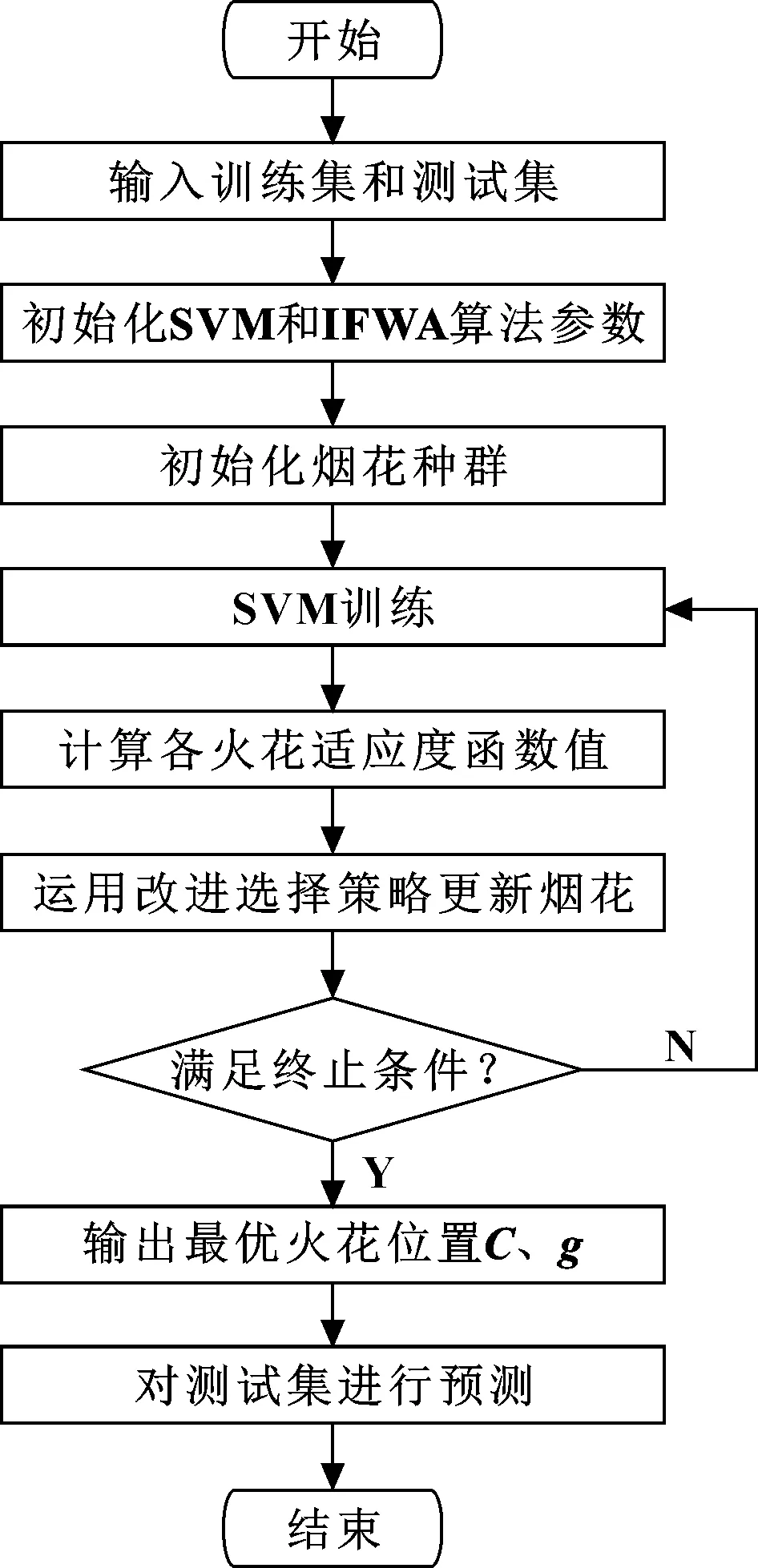
圖1 改進煙花算法優化支持向量機流程
(1)輸入特征矩陣的訓練集和測試集,并歸一化處理;
(2)初始化IFWA相關參數和SVM參數。IFWA相關參數包括:單個煙花爆炸的火花總數上限、下限,高斯變異火花的個數,最大爆炸幅度,火花總數,迭代次數等;SVM模型中主要參數為懲罰因子和核參數;
(3)執行爆炸算子、變異算子以及映射規則等操作,隨機產生初始種群;
(4)將訓練集代入SVM模型中進行訓練;
(5)計算產生火花的適應度,通過改進選擇策略對火花進行篩選,確定下一代煙花種群;
(6)判斷是否滿足算法最大迭代次數,如果不滿足,則循環步驟(4)—(5);否則,終止循環;
(7)輸出最優參數,利用最優的和建立SVM模型,對測試集進行測試。
3 滾動軸承故障診斷實驗分析
本文作者采用美國西儲大學滾動軸承故障診斷公開數據進行實驗分析。采用加速度傳感器在采樣頻率12 kHz、電機負載1.47 kW(2HP)條件下采集不同狀態的軸承數據,其中包括正常狀態下75組信號數據,以及軸承內圈、滾動件、外圈故障分別在故障深度為0.177 8、0.355 6、0.533 3 mm下各25組信號數據,每組信號由4 096個采樣點組成,共300組信號。
3.1 故障診斷模型
提出一種變分模態分解樣本熵與時域指標(TDI-VMD-SE)相結合的特征提取方法和改進煙花算法優化支持向量機(IFWA-SVM)的識別模型,實現滾動軸承的故障診斷。診斷流程如圖2所示。
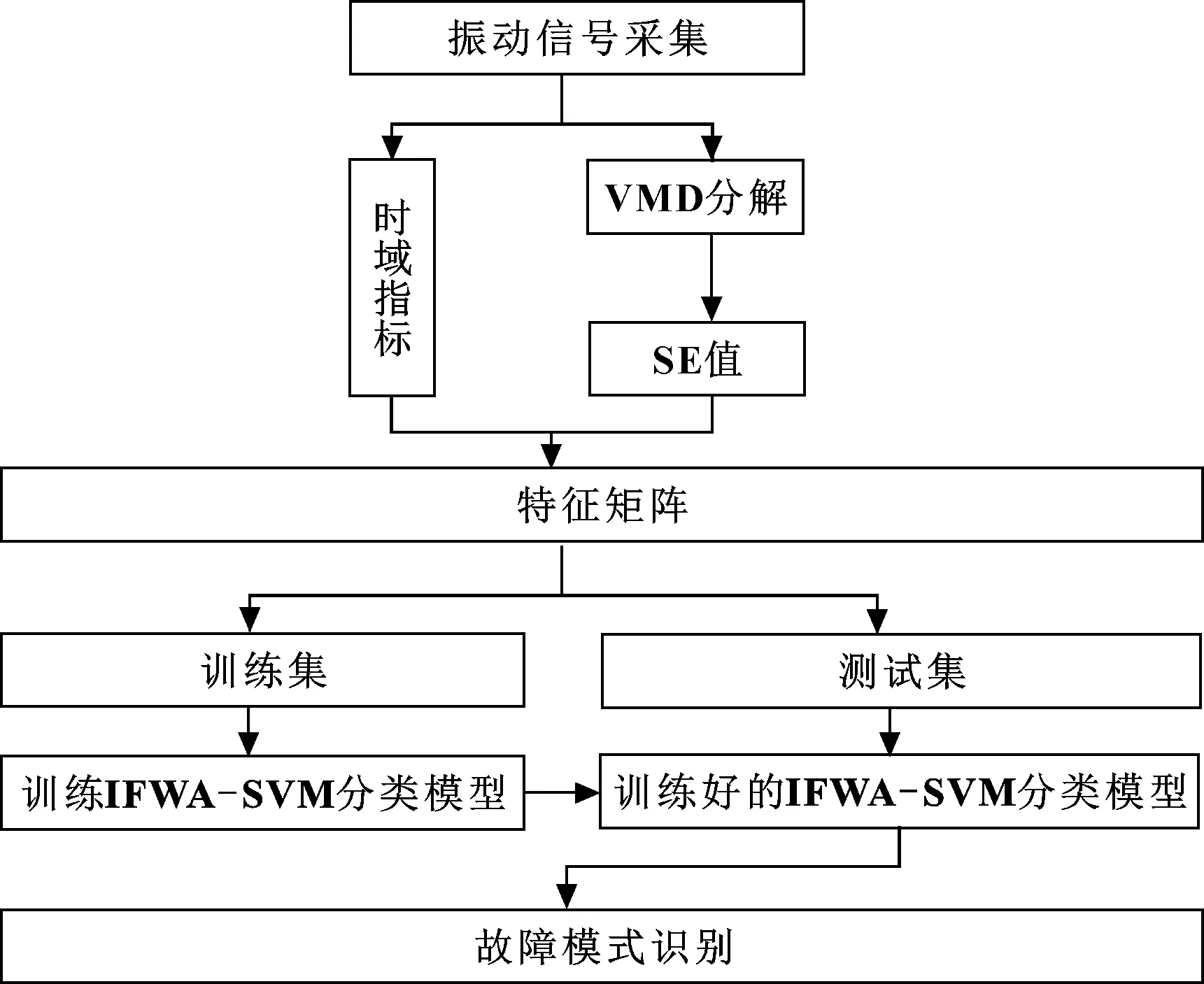
圖2 滾動軸承故障診斷模型
具體步驟如下:
步驟1,振動信號采集:通過振動信號傳感器分別采集滾動軸承在不同狀態下的振動數據;
步驟2,特征值提取:對振動數據進行VMD分解,計算模態分量的樣本熵;另外,計算原始信號的有效值和峭度,將其與各模態分量的樣本熵結合,構建特征矩陣,劃分為訓練集和測試集;
步驟3,故障模式識別:利用訓練集數據對IFWA-SVM分類模型進行訓練,將測試集數據輸入到訓練好的IFWA-SVM模型中,輸出故障類型,完成故障類型的識別。
3.2 振動信號的時域分析
時域指標受軸承技術參數影響較小,在振動信號處理中能夠直觀表現振動信號隨時間的變化。軸承健康狀態改變時,振動能量將增大,且產生不同的沖擊特性。有效值是反映振動數據能量大小的一個時域指標,具有良好的穩定性,但存在感應早期故障的靈敏性差的缺點。峭度指標能夠有效反映振動信號的沖擊特性,相比有效值更能表征前期故障。為防止數據冗余,僅選取有效值和峭度指標作為代表指標進行分析。表1所示為滾動軸承在4種狀態下代表樣本的時域指標。
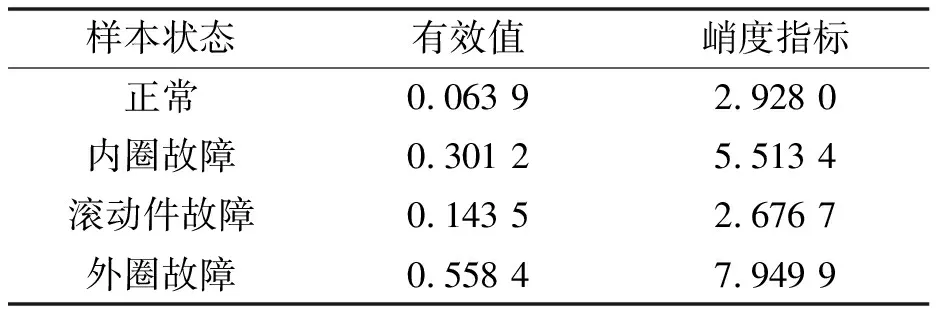
表1 代表樣本振動信號的時域指標
由表1可以看出:正常軸承的有效值和峭度指標均小于故障樣本,滾動件故障軸承有效值和峭度指標有略微的增加,外圈故障軸承有效值和峭度指標最大。由此可見,利用有效值和峭度指標能較好地區分故障類型。
3.3 振動信號的VMD分解及樣本熵分析
由文獻[17]確定VMD分解個數及懲罰因子的值分別為4、2 000。通過VMD分解得到4個固有模態函數,將結果從低頻到高頻排列,圖3、圖4所示分別為正常軸承和內圈故障軸承振動信號IMF對應的時域圖、頻譜圖。可知:各IMF的頻譜分布及頻譜幅值存在差別,僅根據頻譜圖難以直接判斷故障類型。因此,本文作者通過各IMF的樣本熵判斷故障類型。
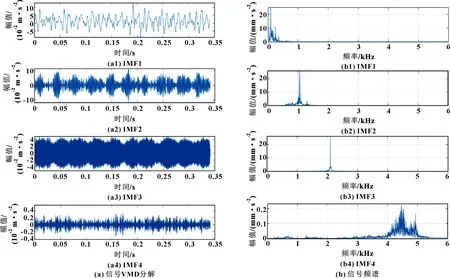
圖3 正常軸承信號VMD分解及頻譜
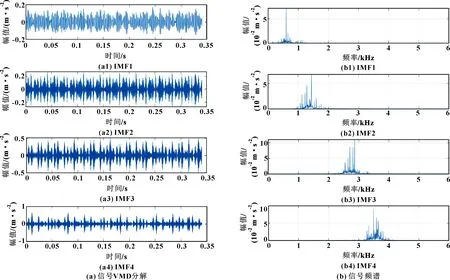
圖4 內圈故障信號VMD分解及頻譜
固有模態函數分量樣本熵統計結果如圖5所示,在IMF1中,正常軸承樣本熵為0.3~0.4、內圈故障的樣本熵為1.1~1.2、滾動件故障的樣本熵為1.3~1.4、外圈故障的樣本熵為0.8~1;軸承外圈故障時各IMF對應的樣本熵值均為最小;在 IMF1與IMF3中,滾動件故障的樣本熵值最大,內圈故障次之,因此IMF的樣本熵可以作為故障類型的判斷條件之一。
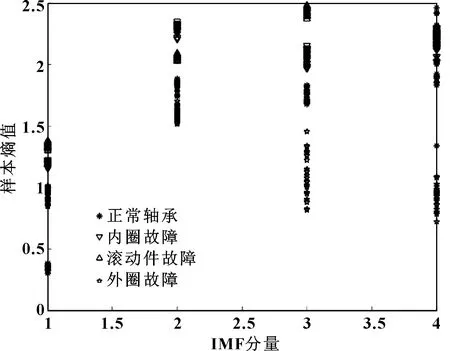
圖5 樣本熵值統計結果
3.4 參數設置及結果分析
將時域指標與IMF樣本熵值結合構建特征矩陣,以3∶2的比例劃分訓練集與測試集,對10種類型進行識別。針對故障類型將標簽設置為:正常狀態為0,根據故障點蝕直徑分別將內圈故障標簽設置為1、2、3,滾動件故障標簽為4、5、6,外圈故障標簽為7、8、9。選用IFWA對SVM的懲罰因子及RBF核參數進行尋優,其中:SVM參數、的變化范圍均為[0.01,100];IFWA火花總數為20、爆炸半徑為10,爆炸數目限制因子=0.3、=0.6;高斯變異火花個數為6;迭代次數為100次,并將SVM模型訓練集的5折交叉驗證結果作為適應度,建立IFWA-SVM故障診斷模型。將TDI-VMD-SE特征矩陣的訓練集作為輸入訓練模型,IFWA尋優結果為:最優=17.053 9、最優=2.570 8。改進煙花算法搜尋迭代過程適應度變化如圖6所示,測試集作為輸入預測結果與實際類別進行對比,結果如圖7所示。
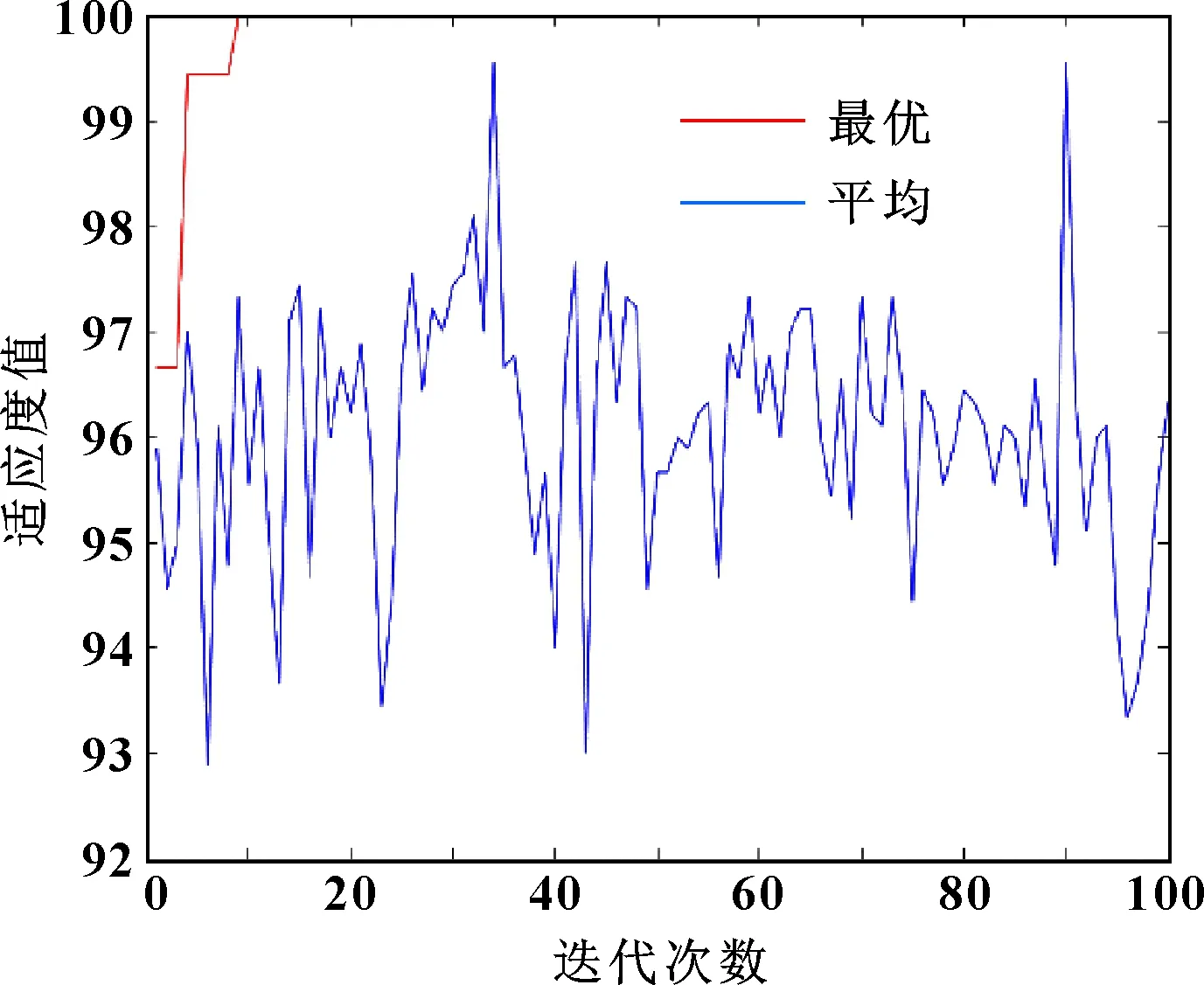
圖6 IFWA搜尋最佳參數適應度曲線
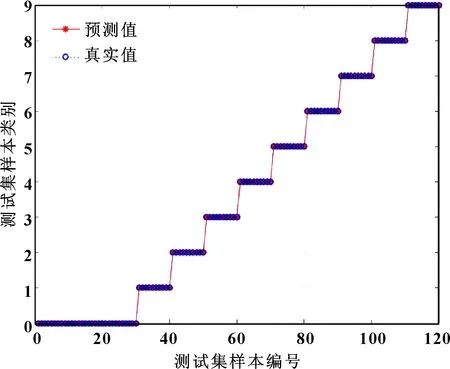
圖7 IFWA-SVM診斷故障與實際故障對比
由圖7可知:TDI-VMD-SE作為特征值時,測試集全部識別正確。另外,通過IFWA搜尋最佳SVM參數,分別對時域特征矩陣、VMD-SE特征矩陣2種特征矩陣輸入進行故障診斷,結果如表2所示。可知:使用有效值和峭度指標作為特征值進行識別和利用VMD-SE作為特征值進行識別時,均有5個樣本被分錯;TDI-VMD-SE特征矩陣包含的故障信息更全面,診斷效果更佳。
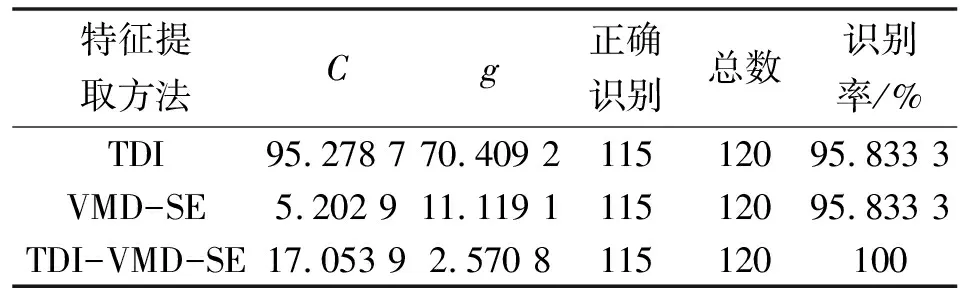
表2 基于IFWA-SVM模型的診斷結果
分別利用粒子群優化算法、未改進煙花算法建立PSO優化SVM、FWA優化SVM的滾動軸承故障診斷模型。參數設置如下:未改進煙花算法的參數設置同如改進煙花算法參數,粒子群優化算法中種群大小設置為20、迭代次數為100次。基于訓練樣本,分別使用IFWA、FWA、PSO優化SVM參數并進行對比。不同算法定量對比結果如表3所示。可知:IFWA的尋優精度優于FWA、PSO,運行時間略長于FWA,但優于PSO。
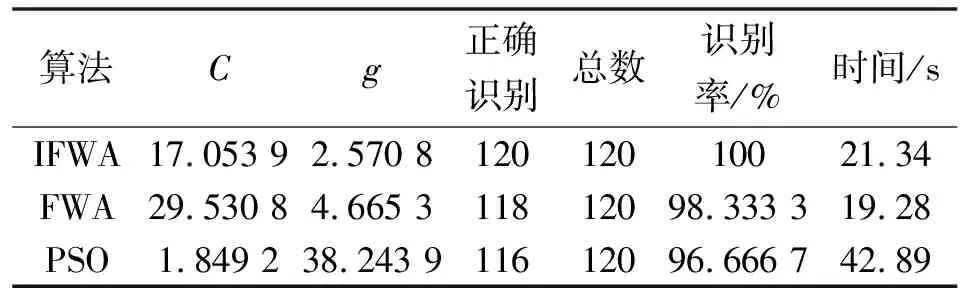
表3 不同算法性能比較
4 結論
(1)使用基于免疫思想的IFWA對SVM參數進行尋優,不僅可以有效提高SVM的分類性能,且訓練時間較短,拓展了SVM參數尋優的方法。
(2)將TDI-VMD-SE特征矩陣作為SVM模型的特征輸入,相比TDI特征矩陣、VMD-SE特征矩陣作為特征輸入,TDI-VMD-SE特征矩陣診斷效果最優。
與PSO-SVM相比,基于VMD和IFAW-SVM模型的滾動軸承故障診斷方法有更高的診斷精度和分類準確率。

