自監督對稱非負矩陣在GDP聚類分析中的應用

劉萬金，趙芳芳

（蘭州財經大學，甘肅 蘭州 730020）

0 引言

國內生產總值（GDP）反映一個國家或地區經濟的變化，作為國民經濟核算的核心指標，具有重要的研究意義。不同省份之間的GDP 各不相同，分析我國GDP的類別差異對解決區域不平衡、提高GDP 具有重要的意義。聚類分析對數據進行無監督劃分，度量不同類別之間的差異性，利用聚類分析方法對我國不同省份之間GDP的研究不斷涌現。吳曉紅［1］利用譜系聚類把我國7大行政區分了3類；范敬雅、鄒玉梅［2］利用高斯混合模型對我國人均GDP 進行聚類，根據貝葉斯準則選取最優聚類數；李澤宇［3］提出基于灰色關聯度聚類分析的我國GDP結構比較；黃賢超［4］將GDP數據劃分為3大產業值，利用Kmeans進行聚類分析；汪飛［5］對我國西部各省區人均GDP、GDP增長率進行聚類分析，分析人均GDP、GDP增長率高低的差異。

非負矩陣分解（Nonnegative Matrix Factorization，NMF）是將非負約束整合到一般矩陣分解中［6-7］。它的目標是找到維數較低的非負矩陣，使它們的線性組合可以近似原始矩陣。非負定性導致基于部分的表示，因為它只允許添加非否定性元素。具體來說，NMF 利用基矩陣與系數矩陣的線性組合來近似原始數據，其中基矩陣和基向量都是非負的。鑒于非負矩陣分解的優點，非負矩陣分解被廣泛應用于機器學習、數據挖掘與數據處理領域。李軍、鄧育［8］從空間和時間兩個角度出發，采用非負矩陣分解算法對出租車的行為進行聚類分析，進而分析出租車的時空行為特征、省份空間結構及省份出行活動之間的關聯，為省份出租車管理與發展提供參考；盧瑞瑞等［9］將L1/2正則化稀疏約束與能源分解相結合，提出基于用戶用電行為數據的L1/2正則化稀疏約束和同質性約束的能源分解聚類分析方法；馬圓圓［10］等將基于非負矩陣分解的無監督聚類方法運用到甲骨文卜辭數據，進一步挖掘卜詞中存在的潛在信息。余江蘭［11］將核L21范數非負矩陣分解應用于圖像聚類；唐曉芬［12］提出基于最大相關熵距離的非負矩陣分解算法，在基因數據中產生了較好的聚類效果。非負矩陣對線性可分數據效果較好，對于非線性數據，非負矩陣分不能直接應用。對稱非負矩陣分解（Symmetric Non-negative Matrix Factorization，SNMF）［13］是一類特殊的約束NMF，它將記錄樣本成對相似性的親和矩陣分解成聚類指示矩陣及其轉置的乘積，不但對線性數據可分，而且對非線性數據也可分。趙昆［14］等提出基于對稱非負矩陣分解的復雜網絡模糊聚類。對稱非負矩陣分解看作一種圖聚類算法，對變量的初始化很敏感，而初始化矩陣的好壞將嚴重影響其聚類性能。為解決此問題，Jia［15］等人充分考慮SNMF 對初始化的敏感性，提出自監督對稱非負矩陣分解算法（S3NMF）。

函數型數據分析（Functional Data Analysis，FDA）［16］的概念首先由加拿大學者Ramsey 提出，利用函數曲線作為數據分析對象，分析數據的內在結構特性，基于函數型數據的聚類分析被稱為函數型聚類分析（Functional Cluster Analysis，FCA）。N. Coffey［17］利用線性混合樣條和P 樣條平滑之間的聯系消除數據噪聲，利用效應模型對表達譜進行聚類；高海燕［18］提出基于非負矩陣分解和函數型數據相結合的函數型非負矩陣分解類算法；黃恒君等［19］提出同時考慮擬合和聚類效果的函數型聚類一步法；劉寶宇［20］基于函數型視角，對比系統聚類與函數型聚類的優缺點，將我國31省份GDP總值利用函數型聚類分析分為5類。

本論述從非負矩陣角度出發，選取1999～2021 年我國31 省GDP 數據，構造新的親和矩陣，利用S3NMF進行矩陣分解，最后借助Kmeans 對S3NMF矩陣分解的結果進行聚類，得出基于自監督對稱非負矩陣分解的我國31 省GDP 類別分析，同時，基于函數型聚類分析結果進行對比［20］，結合實際數據分析S3NMF 聚類分析的效果。

1 相關理論

1.1 NMF

NMF［20］是將矩陣 X ∈ ?m×n分解為兩個非負矩陣W ∈?m×r和 H ∈ ?r×n(r ? min(m,n))的乘積的一種形式，即X ≈WH。相應優化算法已被來解決NMF 優化問題［21-22］。

NMF 使用歐幾里德距離來測量重建誤差，優化問題如下：

其中‖ ‖.F表示矩陣的Frobenius 范數，X ∈?m×n是訓練集，W ∈?m×r和 H ∈?r×n分別稱為基矩陣和系數矩陣。元素X,W,H 都是非負的。相應的乘法更新規則如下［6］：

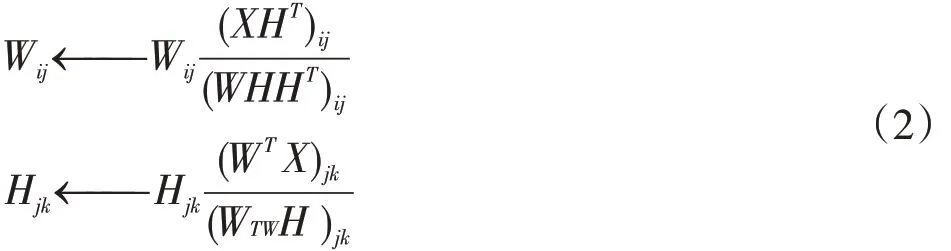
1.2 S NMF

對于n×n 階相似矩陣 A，對稱非負矩陣［13］目標函數為

其中H 是一個大小為n×k 的非負矩陣，k 是聚類數。SNMF與譜聚類（SC）具相近的目標約束函數，相關性較高［13，23］。SC的目標函數為

其中 I ∈ ?k×k是單位矩陣，SNMF 通常被看作圖聚類的一種算法。

2 S3NMF、Kmeans、FCA

2.1 S3NMF

Jia 等人提出 S3NMF 算法［15］，克服了對稱非負矩陣分解對初始化敏感性。首先生成一組隨機非負矩陣（b 是集合的大小），由對稱非負矩陣分解獲得b 個聚類劃分，構造質量更高的相似矩陣。

在不同初始化下生成一組更優聚類劃分。重復該過程，直到達到終止準則或最大迭代次數。約束優化模型為：

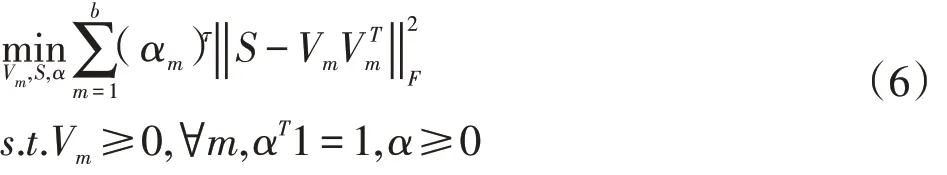
其中，αm是 α ∈ ?b×1的第 m 個元素，權重向量平衡每個分區的貢獻，1 ∈?b×1表示全1向量，約束 αT1=1避免了 α 的平凡解（即 α=0），α ≥0 保證每個 αm都是有效權重，τ ∈(1+∞)。更新規則如下：

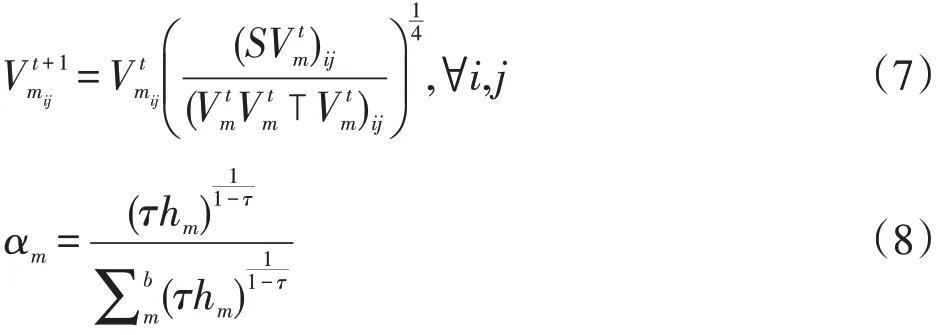
2.2 Kmeans

Kmeans 聚類算法［24］利用不同點之間的歐氏距離來度量不同點之間的相似度。給定固定點，當不同點到固定點之間的距離較近時，則該固定點將與離其最近的一類點被聚到同一個類別中，依次類推，直到樣本中所有點到聚類中心距離最近且類中心不再變化時，最終實現歸類，聚類完成。

Kmeans 聚類算法步驟如下所述：

（1）從樣本中隨機選取k 個類中心。

（2）對剩下的樣本，計算其到類中心的距離，并把離類中心近的樣本與相應的類中心歸為一類。

（3）重新計算各個類的中心。

（4）重復以上2至3步驟直至每個聚類不再變化。

2.3 FCA

函數型聚類基于曲線的相似度進行聚類［20］。第i條曲線xi(t)與第j條曲線xi(t)之間的相似度采用式（9）所定義的曲線距離來度量，也即歐氏距離。

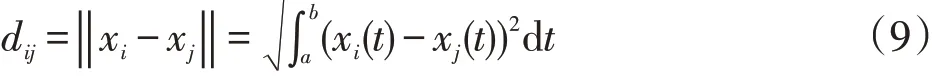
將xi(t)與xj(t)用相同的K 維樣條基函數Φ(t)展開得：

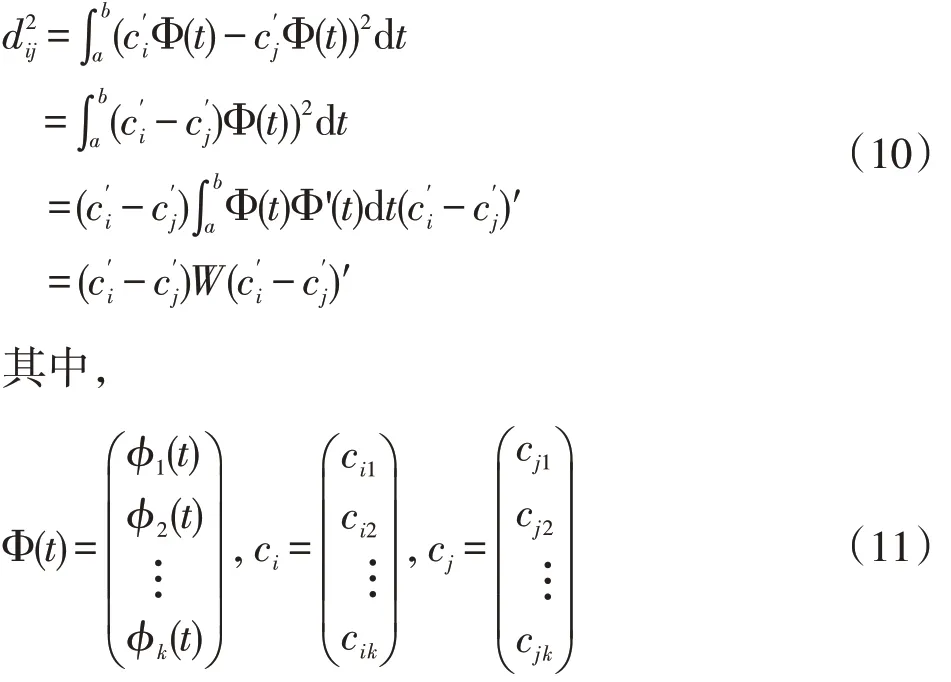
3 聚類分析

3.1 數據來源

我國是一個地域遼闊、人口眾多的發展中國家，利用聚類分析的方法對各省市GDP 指標進行合理的分類，對國家的經濟發展有著重要的現實意義。本論述選取我國 31 省市 1999～2021 年 31 省 GDP 數據進行聚類分析，基于S3NMF 分析我國31 省市GDP 的類別差異。文章數據來源：中國經濟社會大數據研究平臺（https：//data.cnki.net/）。使用計算軟件為：Matlab 2018 b，CPU 配置：Intel（R）Core（TM）i7-10875H CPU@2.30 GHz。

3.2 聚類結果及分析

3.2.1 S3NMF聚類

對我國31 省份GDP 總值數據，構造新的親和矩陣，利用S3NMF 進行分解。Kmeans 利用樣本與樣本之間的距離進行聚類。S3NMF 對分解后的矩陣利用Kmeans聚為5類，聚類結果見表1所列。

表1 S3NMF聚類結果分類表 單位：億元

由表1可知，我國31省市按照GDP總值分為5類，其中上海市、江蘇省、浙江省、山東省、廣東省、四川省為第一類，就第一類省份而言，高新技術產業發達，人才驅動經濟發展；北京市、河北省、安徽省、福建省、河南省、湖南省、湖北省為第二類，就第二類省份而言，經濟產業比較豐富，產業結構較為完善；山西省、遼寧省、云南省、陜西省為第三類，就第三類省份而言，以特色產業為導向驅動經濟增長；內蒙古自治區、江西省、廣西壯族自治區、重慶市、貴州省為第四類，就第四類省份而言，擁有一定優勢資源，沒有明顯強勁產業驅動經濟快速發展；天津市、吉林省、黑龍江省、海南省、西藏自治區、甘肅省、青海省、寧夏回族自治區、新疆維吾爾族自治區為第五類，就第五類省份而言，區位優勢相對較弱，產業結構不完善，人才流失比較嚴重。分析聚類結果可以發現，整理后的聚類出現一定的階梯性，即從第1 類到第5 類整體體現為從東到西整體GDP 由強到弱的變化過程，東部地區GDP總體較高，西部地區GDP整體較低。

3.2.2 FCA聚類

為了對比聚類效果，本論述聚類結果以劉寶宇函數型聚類（FCA）結果為參照進行對比［20］，FCA聚類結果整理后，見表2所列。

表2 函數型聚類結果分類表 單位：億元

由表 2 可知，FCA 將我國 31 省份按照 GDP 總值聚為5類，其中江蘇省、山東省、廣東省為第一類；浙江省、河南省為第二類；北京市、河北省、遼寧省、上海市、安徽省、福建省、湖北省、湖南省、四川省為第三類；天津市、山西省、內蒙古自治區、吉林省、黑龍江省、江西省、廣西壯族自治區、重慶市、云南省、陜西省為第四類；海南省、貴州省、西藏自治區、甘肅省、青海省、寧夏回族自治區、新疆維吾爾族自治區為第五類。

結合表1與表2可知，兩種聚類方法產生的共同聚類結果為：（1）將江蘇省、山東省、廣東省聚為同一類；（2）將北京市、河北省、安徽省、福建省、湖北省、湖南省聚為同一類；（3）將內蒙古自治區、江西省、廣西壯族自治區、重慶市聚為同一類；（4）將海南省、西藏自治區、甘肅省、青海省、寧夏回族自治區、新疆維吾爾族自治區聚為同一類。就表1 與表2 具體聚類效果而言，S3NMF 聚類結果省份類別個數分布比較均勻，兩者聚類方法的聚類結果整體較為接近，但S3NMF 無法直接進行聚類分析，對分解后的矩陣借助Kmeans 進行聚類，非負矩陣分解具有一定的降維作用，因此，基于S3NMF的聚類結果可能存在一定程度的偏差，但相對而言，基于S3NMF的聚類分析能夠產生相對比較準確的聚類劃分。

總體而言，我國經濟發展仍存在區域差異、產業差異、結構差異，東西部地區差異較大，但各省GDP 都存在較大的發展空間，如何提高GDP 及解決區域發展不平衡問題既有機遇又有挑戰，經濟相對落后的省份要取長補短，打造區域特色，提高自身經濟實力，經濟相對較高的城市要不斷促進產業成功轉型，結合自身特色挖掘創新性經濟驅動策略，自身發展的同時帶動西部GDP 發展相對緩慢的城市，從而實現東西部共同發展，促進我國GDP整體增長。

4 結論

S3NMF 利用集成的思想、考慮初值敏感性的同時加入監督信息。利用我國31省GDP數據構造親矩陣，借助Kmeans 對S3NMF分解后的結果進行聚類分析，將我國31省按照GDP分為5類，結合31省自身經濟特色與基于S3NMF 矩陣分解的結果綜合來看，S3NMF 能夠產生相對較為準確的聚類劃分，可以將基于S3NMF 分解的聚類方法應用到未知標簽信息的聚類問題中。