基于CNN-LSTM深度學習的列車荷載與橋面系局部健康狀態識別研究

樸春慧，冀梅梅，張志國，劉玉紅，李智宇，董 現

(1.石家莊鐵道大學 信息科學與技術學院，河北 石家莊 050043；2.河北省電磁環境效應與信息處理重點實驗室，河北 石家莊 050043；3.石家莊鐵道大學 土木工程學院，河北 石家莊 050043；4.北京全路通信信號研究設計院集團有限公司, 北京 100073)

橋梁是交通運輸領域中極為重要的基礎設施和核心樞紐，對我國經濟社會發展有重要的推動作用[1]。為保證橋梁在役時期內的結構安全，避免出現突然性破壞，很多大跨度橋梁安裝了橋梁結構健康監測系統(Bridge Structural Health Monitoring System, BSHMS)。BSHMS通過在橋梁結構關鍵位置處安裝傳感器，采集結構響應數據，通過監測數據大小和變化趨勢判斷橋梁結構特性，進而評估橋梁結構健康狀態。BSHMS在對大跨度橋梁進行監測時，考慮大跨度橋梁結構復雜，通常選擇易收集、監測數據較精準且便于分析研究的靜力數據和動力數據作為監測內容，靜力數據通常包括應變、位移、索力等，動力數據通常包括模態頻率、振型等。

我國BSHMS研究起步較晚，自20世紀90年代起，信息與物聯網技術發展迅速，網速不斷提高，高精度、長壽命傳感器和信號處理設備得以發展，國外一些國家開始將BSHMS技術用于長大跨橋梁結構監測，伴隨我國交通建設的發展和經濟水平的提高，BSHMS研究與應用從最初的示范應用已逐步走向大范圍應用。進入21世紀，我國對BSHMS的發展給予了大力支持，BSHMS的應用范圍在國內不斷擴大，但由于高性能傳感器及監測系統價格居高不下，且橋梁結構工作性能影響因素復雜，一般情況下，BSHMS系統僅建立在典型服役橋梁結構上，在有限的關鍵截面布置測點。例如，我國較早建立BSHMS系統的橋梁有武漢長江大橋、蕪湖長江大橋和上海徐浦大橋等。在上述橋梁為代表的BSHMS中，監測因素主要有橋址周圍的環境信息及關鍵測點的結構響應信息等[2]，對信息技術的使用則集中在監測數據的采集、傳輸和可視化，并未對高時空相關性及大量監測數據挖掘與分析，無法妥善處理與有效利用監測數據，難以通過監測數據有效判定橋梁結構健康狀態和損傷識別，限制了BSHMS對橋梁狀態評判和維修策略選擇的指導作用。因此，對于海量高時空相關性的監測數據來說，充分挖掘其潛在價值是當下BSHMS亟待解決的問題。

BSHMS采集的應變大小與變化趨勢能夠直接反映橋梁結構的受力和形變狀態，進而分析出橋梁結構局部健康狀態。通過分析實測應變數據得出橋梁列車荷載和局部結構健康狀態有重要意義，列車荷載識別對列車荷載標準的制定、橋梁耐久性和安全性評估具有重要作用，通過大型列車荷載識別能夠充分發揮BSHMS的作用，降低大跨度橋梁列車識別的成本；橋梁局部結構健康狀態識別為發現橋梁結構的潛在損傷，降低橋梁事故帶來的重大損失，及時采取結構維修、加固等措施具有關鍵作用，對實現橋梁結構健康狀態監測與服役性能評估提供有力支持[3]。近年來，在利用橋梁健康監測數據進行列車荷載和健康狀態識別等方面進行了一些探索。如，左小晗[4]以橋梁動應變響應為研究對象，實現了車軸信息的檢測，并對多列車過橋時車輛軸重和總重進行了研究。劉澤佳等[5]采用基于小波臨界系數和應變閾值的超重車荷載識別方法，利用橋梁有限元模型得到超重車荷載應變閾值，使用應變數據實現了珠江黃埔大橋北汊斜拉橋超重車荷載信號識別。楊慧等[6]通過車輛過橋時采集的動應變響應，使用BP神經網絡方法實現了簡支梁橋車輛荷載位置、車速以及軸距的識別，驗證了神經網絡方法進行車輛荷載識別的可行性。Kromanis等[7]提出通過建立溫度與應變之間非線性關系的支持向量回歸損傷識別方法，將預測誤差作為損傷敏感特征，用某鋼筋混凝土橋連續6年的溫度和應變監測數據中前3年數據進行模型訓練，后3年數據驗證模型的損傷識別效果。何浩祥等[8]提出基于CNN的橋梁損傷識別方法，通過試驗證明了CNN除可以高精度提取橋梁結構損傷敏感特征指標外，還能夠比較精準的識別橋梁結構損傷情況。Ni等[9]提出一種基于CNN的異常數據檢測方法，通過試驗對方法的適用性進行了檢驗，試驗過程使用了某橋梁的BSHMS實測加速度數據，試驗結果表明，該方法對于異常檢測有著較高的精準度。楊杰文等[10]將深度學習算法用于橋梁裂縫檢測，通過試驗證明所提模型能夠實現復雜環境下的裂縫檢測。趙欣欣等[11]將卷積神經網絡應用于橋梁高強螺栓失效識別，通過實例證明所提方法的準確性。王飛球等[12]提出基于BP神經網絡的橋梁安全風險評估模型，并使用信江特大橋BSHMS數據進行了驗證，結果表明，該模型具備一定的可行性。

綜上所述，目前對BSHMS數據進行挖掘與分析已漸漸成為當下研究熱點之一，盡管開展了不少研究，但是仍受監測測點數量有限，監測數據受環境等因素影響，存在數據深度挖掘分析不夠，反饋橋梁狀態信息不足及實際監測數據利用率不夠等問題。本文針對上述問題，試圖探索一種利用少量監測數據進行橋梁列車荷載識別和局部健康狀態判別及預警的方法，以提高監測數據的使用效率。因此，本文利用應變對大跨度橋梁的荷載響應、橋面系局部損傷敏感的特性及結構響應之間的相關性，使用某大跨度鋼桁架橋BSHMS實測數據作為數據集，對數據集中的車致應變進行提取；構建列車荷載系數，對該橋經過的列車車型和列車荷載進行識別；提出一種基于CNN-LSTM的橋面系局部健康狀態識別方法，通過分析監測數據之間的相關性，確定CNN-LSTM模型的輸入量與輸出量；使用歷史監測數據訓練CNN-LSTM模型，構建反映橋面縱梁測點應變監測數據間相關性的函數關系；在橋面系測試節間縱梁性能退化出現損傷時，通過預測應變值偏離實測值的程度實現橋梁健康監測損傷預警。

1 車致應變提取

通過應變與應力關系可以將BSHMS中的應變數據轉為應力，進而得到橋梁結構在外力作用下內部產生的力，以進行列車荷載和橋面系局部健康狀態識別。BSHMS在實際工程監測采集到的應變數據混合了溫度引起的應變數據(溫致應變)和車致荷載應變數據(車致應變)，這兩種應變一般同時存在，無法分開測量，故BSHMS中的應變數據為車致應變和溫致應變的綜合[13]，在利用應變進行工作狀況、列車荷載及局部損傷識別時，需要將溫致應變分離出去。此外，由于BSHMS采集數據時，受傳感器的性能、網絡信號波動等方面影響，監測數據可能存在缺失、異常等情況，影響列車荷載和橋面系局部健康狀態識別的準確性。因此，進行車致應變提取前，需要對監測數據進行預處理。

1.1 數據來源

本文數據集來源于某大跨度鋼桁架公鐵兩用橋的BSHMS系統，為能夠及時掌握橋梁結構受力與健康狀態，該橋的BSHMS關鍵測點位于橋梁第二聯，并由此擴展至全橋。該橋BSHMS系統監測內容和測點部署信息見圖1，主要監測內容為[14]：

(1) 過橋列車信息監測：包括列車駛進、駛離該橋梁時的列車速度以及列車的軸數與軸距等信息。

(2) 橋址環境監測：包括橋梁所在地的溫度與濕度，橋上鋼軌的溫度、溫度場等。

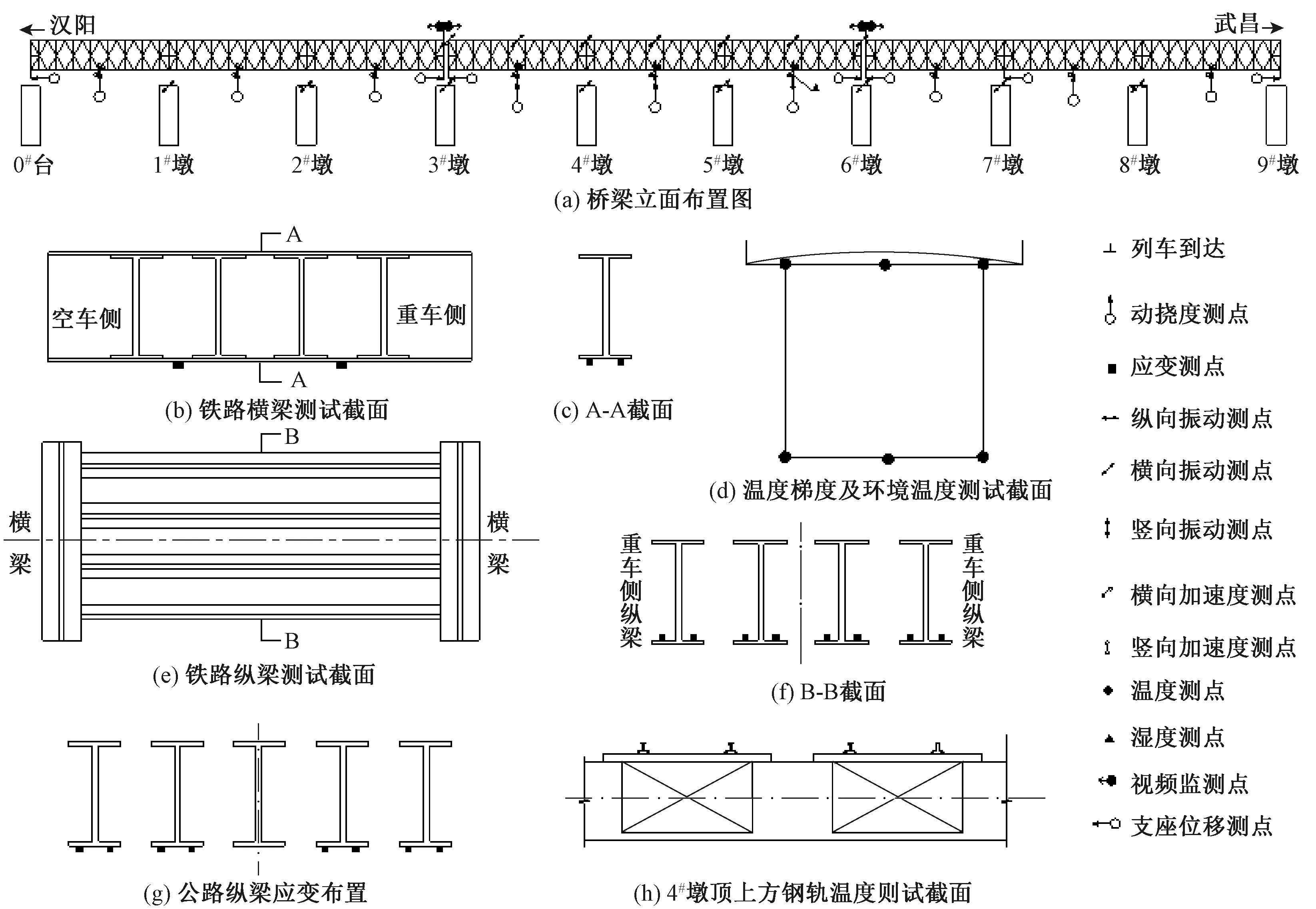
圖1 測點位置分布

(3) 橋梁典型截面應變及列車(車輛)荷載監測：包括橋上鐵路橫梁與縱梁截面關鍵點的應變、橋上公路縱梁截面關鍵點的應變、鐵路/公路線路列車或車道車輛荷載等。

(4) 橋梁結構動力特征監測：包括橋梁主梁結構的振動特性以及加速度數據等。

(5) 橋梁結構使用性能監測：包括橋梁主跨跨中撓度、橋梁支座位移等。

本文所用數據為某大跨度鋼桁架橋第二聯鐵路縱梁2010年9月至2010年10月采集的應變數據，共1 046 598條。應變數據為觸發式采集，即當列車駛進橋梁時傳感器立即打點采集應變，當列車駛離橋梁時結束采集，每條應變數據包括第二聯鐵路縱梁S1～S8共 8個測點監測到的應變數據。

1.2 缺失值填補

在本文使用的數據集中數據缺失率約為8.3%，且缺失類型多為單點缺失，因此本文僅對單點缺失數據進行處理，對于連續缺失數據則直接剔除該條數據。缺失值的存在造成數據的時空相關性降低，使用含缺失值的數據集進行列車荷載與健康狀態識別，不僅難以反映列車荷載與橋梁真實運營狀況，還會降低準確率，因此，對數據集中的單點缺失本文使用平均值法進行填補，即取缺失數據前后時刻數據的平均值進行填補，該方法不僅能使數據曲線保持不變，又能最大化利用當前數據信息，計算方法為

(1)

式中：xi為缺失值；xi-1和xi+1分別為缺失值前一個時間點和后一個時間點的數值。

1.3 數據歸一化

歸一化操作可以將監測數據歸約到[0,1]內，不僅可以防止神經網絡訓練時出現過擬合現象，還可以使其收斂更加快速。本文歸一化方法選擇了當下較為流行的Min-Max標準化方法，該方法依據線性變換原理將測得的原始數據進行處理，并將數值映射至[0,1]之間，即將BSHMS監測得到的數據轉換至[0,1]范圍內，歸一化基本公式為

(2)

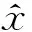
以部分應變數據為例，歸一化前后見圖2。由圖2可知，歸一化前應變值基本在[0,250]，而歸一化之后應變值均在[0,1]區間內。

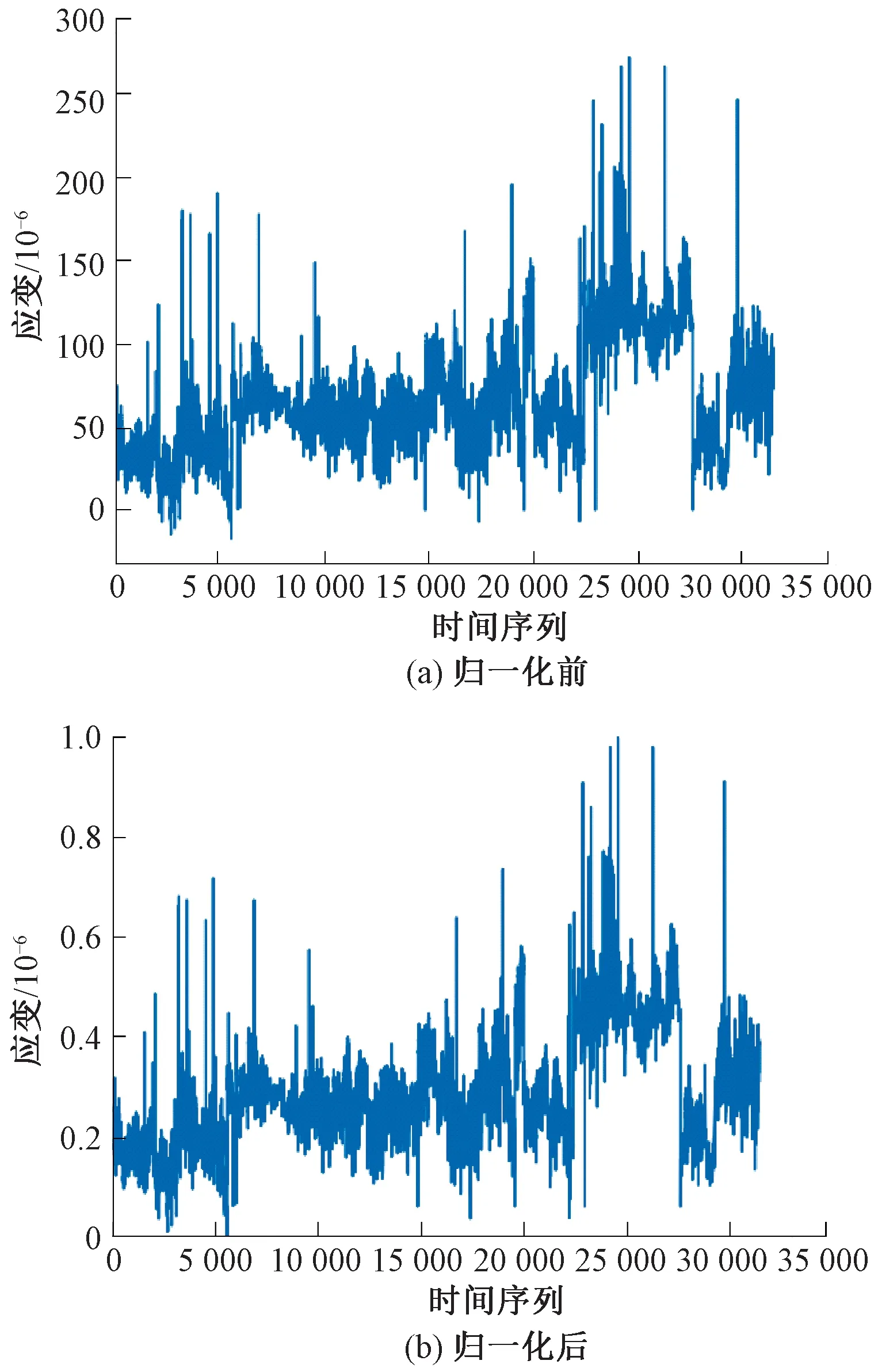
圖2 數據歸一化前后對比圖

1.4 異常數據檢測

BSHMS中異常值判別標準為明顯不滿足橋梁結構受力狀態的數值，具體表現為離散型，即距絕大多數監測數值較遠。本文采用孤立森林算法(Isolation Forest, IF)作為數據集中異常數據的處理方法，利用IF算法進行數據處理，具有速度快、時間復雜度低、對物理設備內存要求較低等優點，與BSHMS中的海量數據處理要求相契合[15]。IF算法認為，在數據集中孤立的點能夠被當作異常值，其具體表現為距離高分布密度群體較遠并且分布密度較為稀疏的點。異常數據檢測結果見圖3(a)，圖中標紅部分(加圈點)為孤立森林算法檢測出的異常值；圖3(b)為使用該方法處理異常值后的數據。由圖3可知異常數據處理歸一化后的監測數據取值區間由[0,1]變為[0.1,0.5]，處理效果明顯。

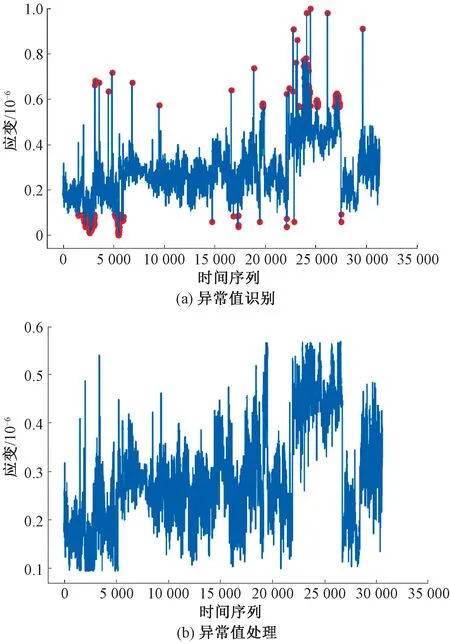
圖3 異常值識別與處理結果

1.5 提取車致應變

BSHMS應變數據中包含了車致應變和溫致應變，為分析橋梁在運營狀態下，車致應變對橋梁結構局部受力作用及影響情況，需剔除應變數據中的溫致應變，保留車致應變[16]。常用的剔除溫致應變方法有經驗模態分解法(Empirical Mode Decomposition，EMD)和小波分解法。其中，小波分解法由于需設定小波基，致使車致應變提取存在誤差；EMD方法則是根據數據集本身的時間序列特性對數據進行分解，與其他方法相比，其優點是不用預先設定基函數，該處理方式使得EMD方法在處理不平穩、非線性特性數據序列方面具備明顯優勢，且具有很高的信噪比，被廣泛應用。對信號序列直接采用EMD方法進行分解時，存在模態混疊問題，為解決該問題，在原始數據中多次加入白噪聲，然后再進行EMD分解，即集合經驗模態分解(Ensemble Empirical Mode Decomposition, EEMD)算法[17]，EEMD算法步驟如下：

Step1將白噪聲n1(t)加入原始應變數據ε(t)中，形成新的應變數據ε1(t)。

Step2使用EMD方法對ε1(t)進行分解處理，即可以得到多個有關本征模函數IMF1(Intrinsic Mode Function，IMF)。

Step3重復Step1和Step2，依次加入不同的白噪聲nn(t)。

Step4計算IMF1～IMFn的平均值，得到最終結果IMF。

本文使用EEMD方法分解了S1測點采集的應變數據，分解前S1測點應變數據見圖4，分解后S1測點應變數據見圖5。由圖4和圖5可知，使用EEMD方法分解應變數據后，原始數據被分解為9個不同的IMF，溫致應變隨溫度變化會呈現出較為明顯的變化趨勢，圖5中后3個IMF分量變化趨勢明顯，因此根據其規律可以判斷出后3個IMF分量是由溫度變化所致。將溫致應變剔除后的車致應變見圖6，可以看出車致應變不存在明顯趨勢項，故可認為溫致應變已剔除。

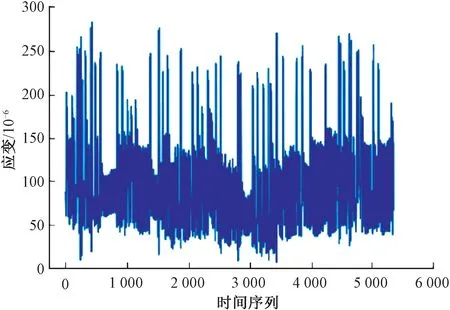
圖4 S1測點于2010年9月1日應變數據序列

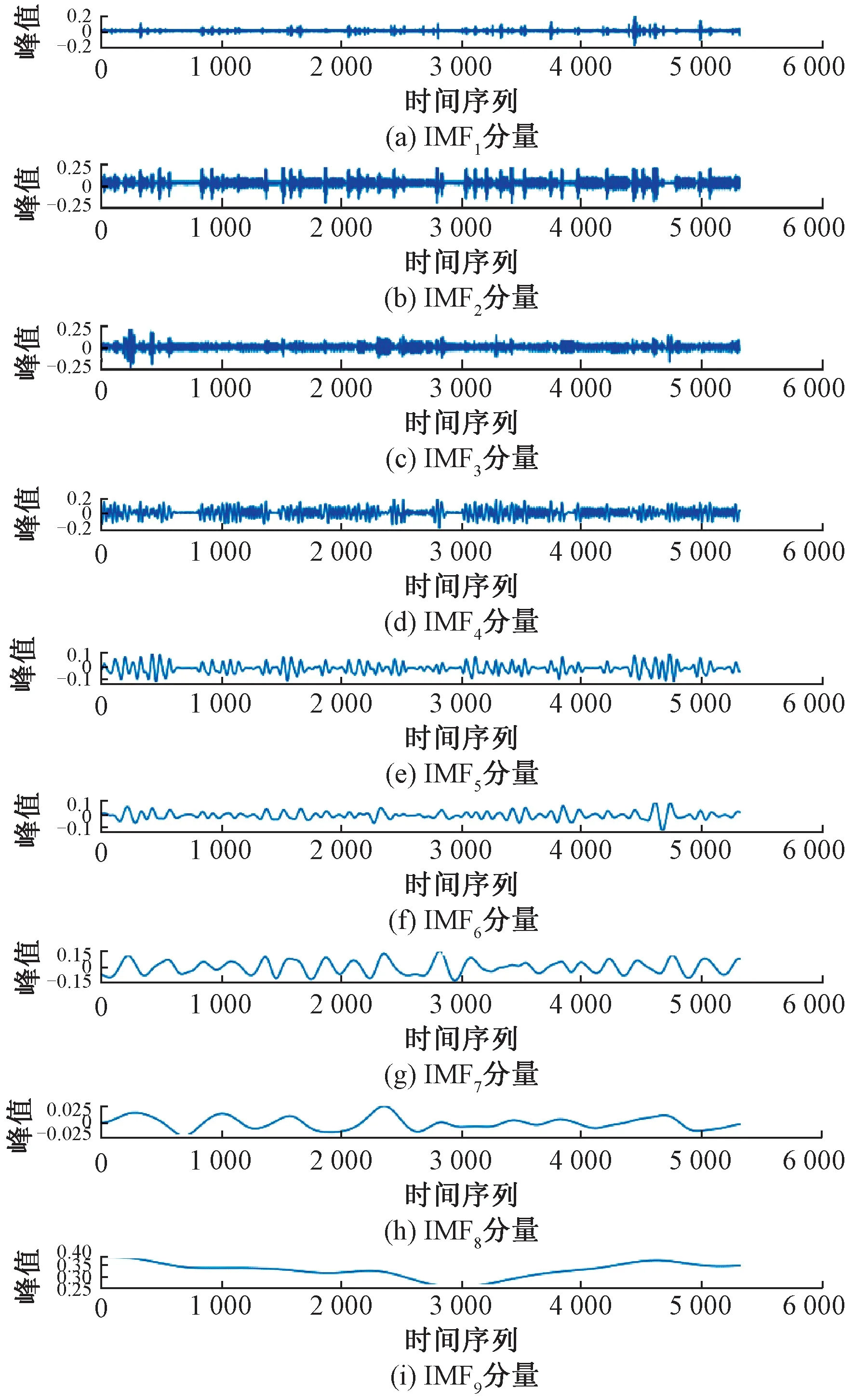
圖5 EEMD方法分解的IMF分量

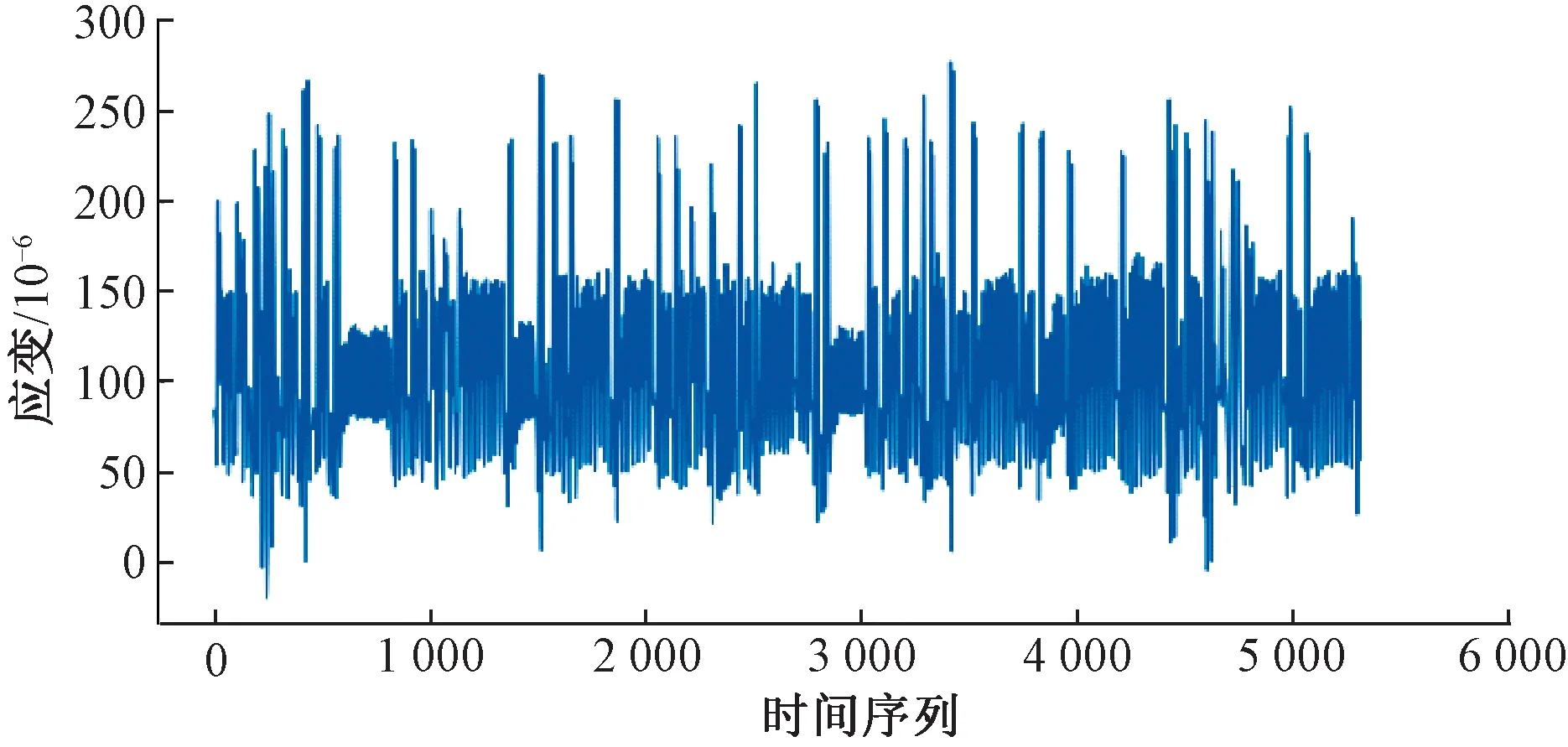
圖6 S1測點于2010年9月1日車致應變序列

2 列車荷載識別

2.1 列車荷載系數

目前，經過該大跨度鋼桁架橋的電力機車車型有5種，各車型參數見表1。

表1 車型參數表

列車荷載識別問題是一個第二類逆問題，即已知橋梁對列車荷載的響應，計算導致響應的荷載。對于列車荷載的識別，本文對車頭上橋至車尾離橋時間段內的應變曲線進行x軸積分，得到應變曲線的影響面積[18]為

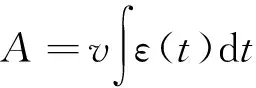
(3)

式中：A為應變曲線的影響面積；ε(t)為應變曲線，t為時間；v為車速，該橋結構健康監測系統包含了車速監測，因此不需對車速進行計算。

在橋梁任意截面測點上，均存在以下關系[19]：

(4)

式中：G1、G2分別表示不同的列車荷載；AG1、AG2分別為對應列車經過時應變曲線的影響面積。因此，本文定義列車荷載系數m為

(5)

由公式(5)可知，同一截面內，列車荷載系數m應為一個常數，受橋梁的結構、材料等因素影響，若橋梁結構處于健康狀態，m的變化范圍較小。若橋梁結構出現損傷時，m會發生較大變化。在不考慮列車荷載橫向分布的前提下，僅需知道鐵路橋梁橋面系縱梁任意測點的應變曲線影響面積和基準列車重量，就能夠實現列車重量的識別。

2.2 有效性驗證

采用上述方法進行某鋼桁架橋列車荷載識別，通過傳感器采集的應變數據進行荷載反推。鐵路橋梁上運行的為多軸車，應變曲線表現為多個峰值。經分析，車頭經過傳感器安裝位置時應變峰值最大，因此，通過分析應變曲線中應變峰值判斷車頭位置進而與表1中電力機車型號進行匹配得出列車荷載系數m。使用2010年5月份S1測點的最大應變峰值，計算影響面積A1=312.5，進而得出列車荷載系數m=0.48，使用該系數對該測點5月份其他應變峰值進行列車荷載識別，部分結果見表2。

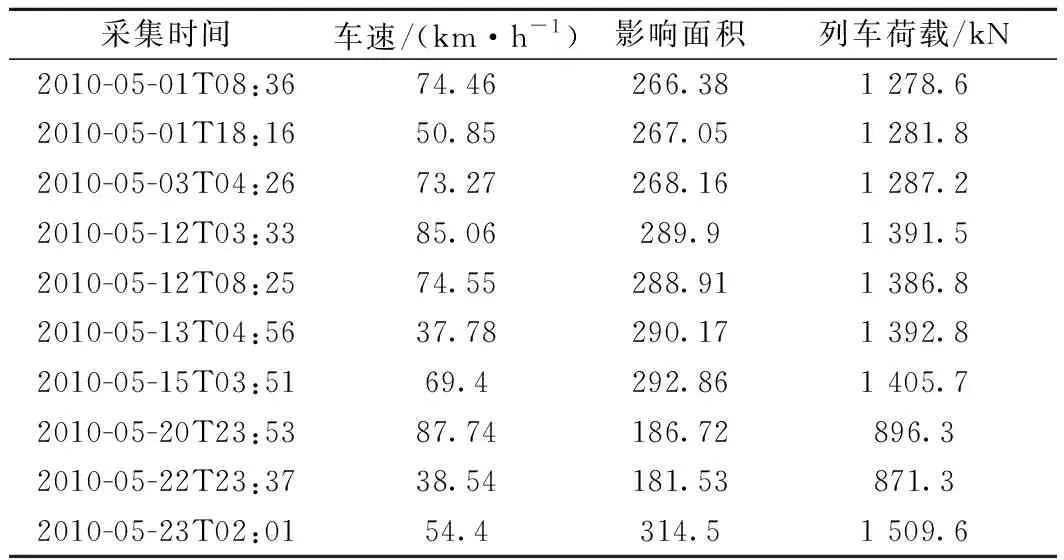
表2 列車荷載識別結果

由表2可以看出，由列車荷載系數m=0.48計算出的列車荷載結果，與表1中給出的經過該橋的電力機車整備重量差別較小。為進一步判斷列車荷載系數的合理性，對S1測點2010年5月全部監測結果進行列車荷載識別，識別結果見圖7。

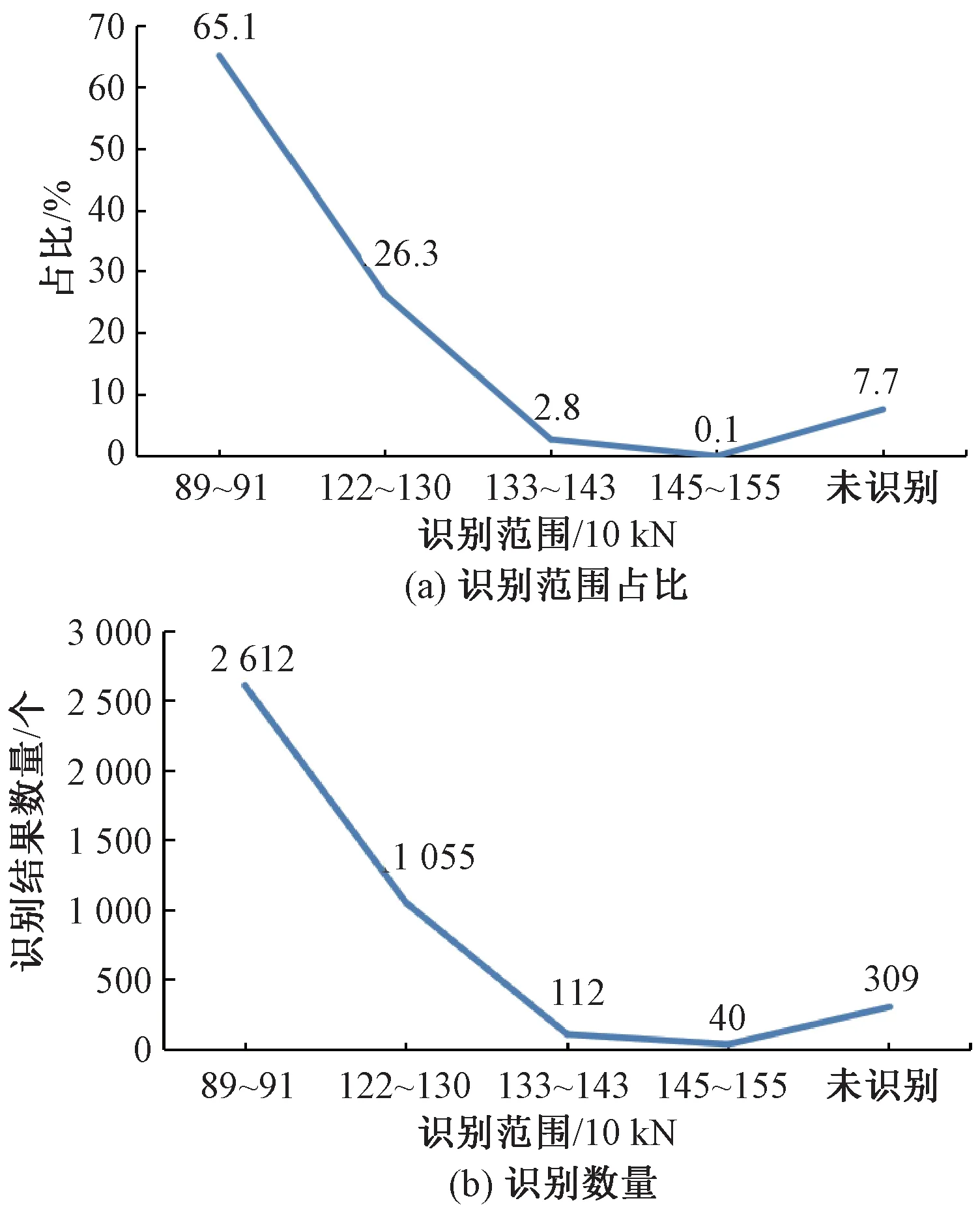
圖7 識別結果

我國電力機車生產廠家對列車整備重量的誤差范圍為3%，因此，以列車標準整備重量的±3%作為誤差值。由圖7可以看出，經過該橋列車荷載識別率為92.3%。由此可以得出，使用列車荷載系數m=0.48作為該橋健康狀態下列車荷載識別的根據是有效的。此外，該方法除了能夠識別電力機車荷載之外，還可對各車廂荷載進行識別，進而得知橋梁上通過的整車荷載。在后續橋面系局部健康狀態識別時，可以使用上述方法計算出的車重排除列車荷載原因造成的應變異常情況，使得橋面系局部損傷判斷更為準確。

3 CNN-LSTM橋面系局部健康狀態識別模型構建

本文提出的基于CNN-LSTM的橋面系局部健康狀態評估模型主要分為以下幾個步驟：

Step1橋梁結構健康數據采集與模型變量確定：使用橋梁健康監測系統采集監測數據，使用對橋面系局部損傷敏感的應變響應數據作為目標變量。

Step2模型訓練與參數設置：訓練CNN-LSTM模型，通過交叉驗證的方式確定模型最優參數。

Step3結構損傷預警閾值設定：將模型預測值和實測值殘差作為觀測值，通過EWMA確定結構損傷預警閾值。

Step4損傷預警的判斷：將橋梁結構監測數據輸入CNN-LSTM模型，通過判斷預測殘差是否超過所設閾值進行損傷預警。

3.1 CNN-LSTM模型構建

目前，多數深度學習模型特征提取方法各有不同，CNN方法的特征提取主要是通過卷積核提取輸入數據的空間相關性特征，但CNN存在濾波器的限制，致使CNN無法獲得輸入變量中的時間相關性；LSTM方法加入了記憶單元和門控制思想，加入后能夠使LSTM模型充分學習輸入數據序列前后數據之間的依賴特征，進而獲得時間相關性，彌補CNN的缺陷，因此本文將CNN與LSTM進行串接，構建出CNN-LSTM預測模型識別橋面系局部損傷。

模型輸入量為安裝在某大跨度鋼桁架橋橋面縱梁測點應變傳感器采集的應變值，輸出量為安裝在同截面對稱位置傳感器采集的應變值，圖8為本文提出的CNN-LSTM神經網絡預測模型結構。由圖8可知，模型分為CNN-LSTM層和全連接層兩個主要部分，其中，CNN-LSTM層為核心層，包括CNN網絡部分和LSTM網絡部分，共計5層網絡層，7個輸入維度和1個輸出維度。在模型中CNN網絡部分，包括卷積層、池化層各一層，CNN網絡部分的核心作用是提取輸入時間序列中的數據特征。LSTM網絡部分有3層LSTM網絡，各層的神經元數量依次為16、32、64，此外各層LSTM網絡間還添加了dropout，用以避免模型過擬合情況出現。全連接層則用于輸出預測的應變數據。

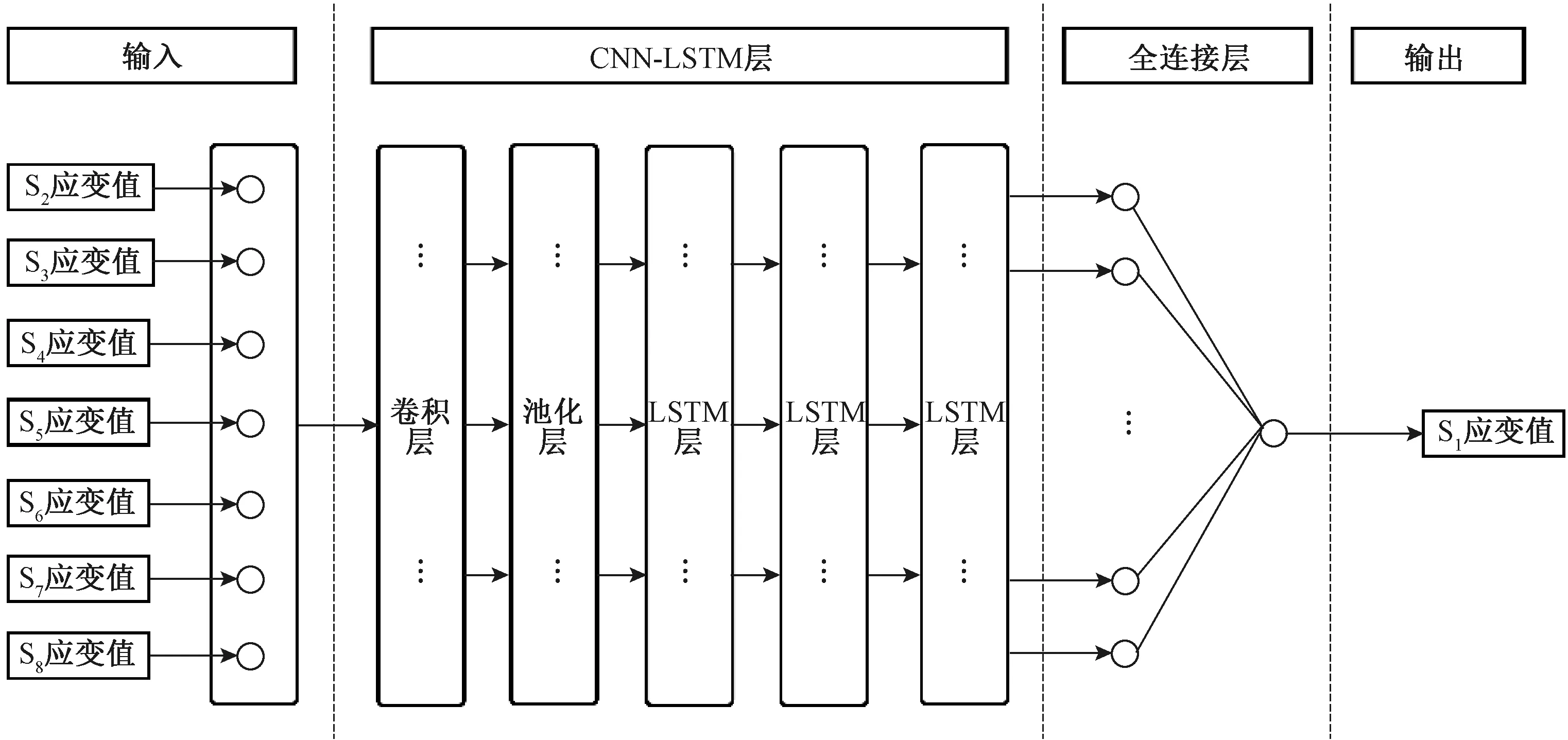
圖8 CNN-LSTM神經網絡預測模型結構圖

3.2 模型參數選擇

本文在CNN參數設置的基礎上[20]，對CNN-LSTM神經網絡預測模型的網絡結構參數進行多次調整，最終確定了具體參數，見表3。

CNN-LSTM神經網絡預測模型的超參數設置是否合理，關乎模型預測精準度的高低，故選擇合適的模型超參數至關重要。比較常見的模型超參數選擇方法有網絡搜索法、貝葉斯優化、遺傳算法以及交叉驗證法等[21]，本文使用CNN-LSTM神經網絡預測模型和橋梁結構健康監測數據對橋梁結構狀態進行預測，涉及數據量龐大，因此在參照現有設計準則[22]的同時，經多次試驗確定了模型的最優超參數為：模型的最大迭代次數(max epochs)為300，迭代時使用早停止準則，即當模型損失沒有提升時停止訓練；模型的學習率為0.001；batch size為1 024。

3.3 預警閾值設置

訓練好的CNN-LSTM網絡模型用來表征橋梁健康監測系統采集的應變數據之間的函數關系。當橋面系測試節間縱梁出現損傷時，橋面系縱梁關鍵測點應變值會增大，使用CNN-LSTM神經網絡預測模型，利用測點對稱性原理對S1測點應變數據進行預測時，預測結果與實際測量應變數據必然會存在較大誤差。

當橋梁處于健康狀態時，CNN-LSTM神經網絡預測模型所預測殘差數值變化范圍固定在某一個區間內，隨著橋梁在役時間的延長，橋梁結構狀態會隨之改變，預測殘差數值也一同增長。因此，根據實時監測數據進行預測時，預測殘差數值的變化程度在橋梁結構健康狀態評估工作中有重要的參考價值。本文通過設置閾值控制線對預測殘差數值進行計算，閾值控制線則使用指數加權移動平均(Exponentially Weighted Moving-average，EWMA)方法來確定。在測試階段，若預測殘差大于健康狀態下閾值控制線，說明橋梁結構已經出現損傷，BSHMS等在線監測程序就會對橋梁損傷情況及時自動預警。

對某一個時間序列{y(1),y(2),y(3),…,y(t)}來說，EWMA的統計量St為

St=λy(t)+(1-λ)St-1

(6)

式中：t為時間；λ為歷史監測數據對當下EWMA的統計權重，取值范圍通常在(0,1]，本文則選擇0.2作為其取值大小[23]。

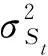
(7)

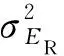
由以上各關系，可以進一步得出橋梁損傷預警的閾值LU(t)控制線計算公式為

LU(t)=μSt±LσSt

(8)

式中：L通常取值為3[24]；當St超過閾值LU(t)時，系統發出預警。

4 CNN-LSTM橋面系局部健康狀態識別模型試驗及結果分析

4.1 監測數據相關性分析

為了驗證溫度與應變、不同測點應變值之間的相關性，對集中的數據進行相關性分析，圖9展示了本文試驗數據中的一部分應變數據與溫度數據隨時間變化曲線。由圖9可以看出，應變數據的變化趨勢與溫度的變化趨勢相似，并且應變數據變化趨勢存在一定的滯后性。由于本文所用數據集均來自鋼桁架橋同一縱梁應變傳感器，且傳感器采用對稱布設，因此可以通過計算S1～S8測點實測應變數據的相關系數，進行不同測點應變測試結果相關性驗證，當相關系數值越大時，可說明測試數據的相關性越強，反之亦然，通過計算得出相關系數見表4。由表4可以看出，溫度與應變之間、不同測點間應變存在較強的相關性。為分析橋梁在運營狀況下的局部受力情況，剔除溫度對應變響應相關性的影響，本文使用EEMD算法成功提取了BSHMS系統中應變數據中的車致應變。

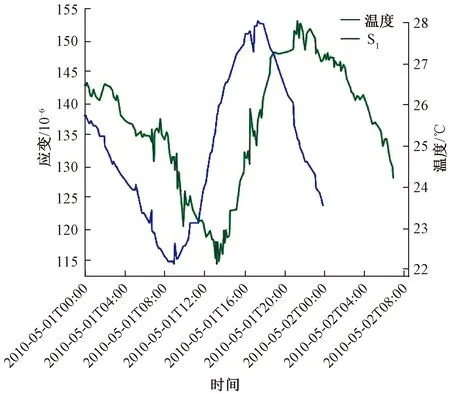
圖9 應變與溫度變化曲線

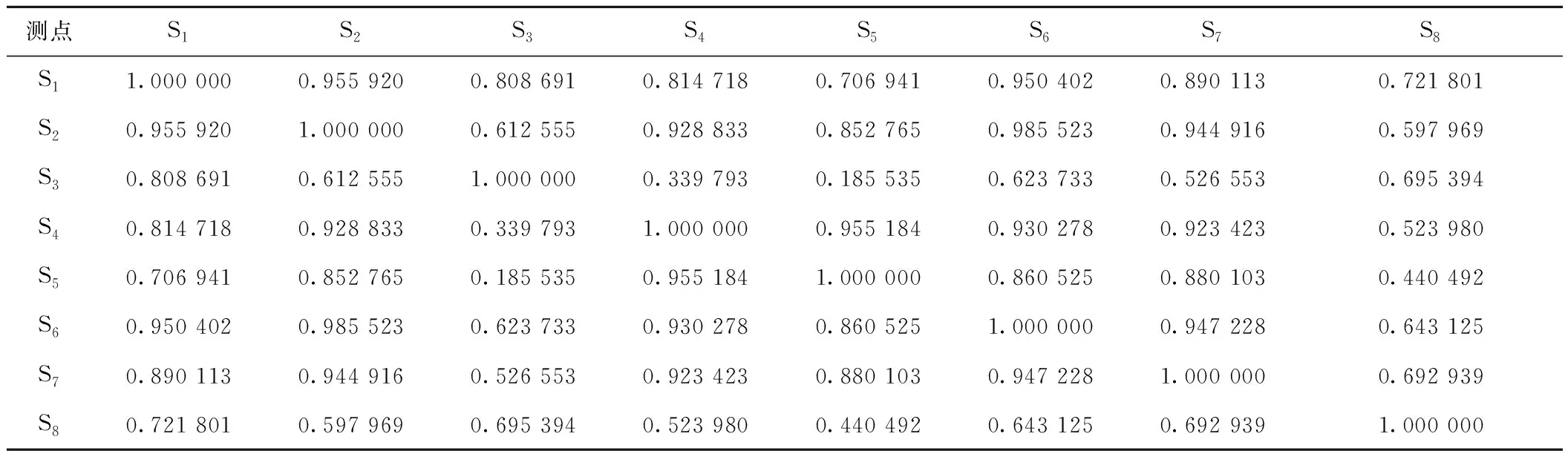
表4 相關系數

4.2 數據集劃分

本文選取實測數據集的80%作為CNN-LSTM神經網絡預測模型的訓練數據集，剩余20%作為驗證數據集。當橋梁上通過一定列車荷載，橋面系縱梁出現開裂、剛度退化等情況時，縱梁的應變值會隨之增加，基于此，本文在模型橋梁結構損傷預警分析階段，通過增大應變值模擬橋面系縱梁結構損傷[25]，具體計算公式為

εd=ε+η·εr

(9)

式中：εd為橋梁出現損傷時的應變值，即橋梁性能的退化程度；ε為橋梁結構中橋面系縱梁測點實際測量的應變數值；η為一個百分比系數，用來表征橋梁結構中橋面系損傷情況的嚴重程度，當取值為0時表示橋梁處于正常狀態，大于0表示橋梁出現損傷，且數值越大損傷程度越嚴重；εr代表橋梁結構中橋面系縱梁應變數據的變化范圍。

4.3 試驗平臺及評價指標

本文試驗使用的物理機處理器為Intel i7-8700，內存為32GB，CNN-LSTM神經網絡預測模型通過Python實現，使用基于Keras的深度學習工具Tensorflow作為框架。

評價深度學習模型性能的指標有許多，使用評價指標能夠很好地量化深度學習模型性能的優劣，本文經過調查研究時間序列預測文獻等，最終選擇平均絕對誤差eMAE和均方根誤差eRMSE作為CNN-LSTM神經網絡預測模型性能優劣的指標評價[26-28]，計算公式分別為

(10)

(11)

式中：N為樣本個數；Xact(i)為實測值；Xpred(i)為模型反歸一化后的輸出值，即模型預測值，Xpred(i)表達式為

Xpred(i)=X′(i)[X′max(i)-X′min(i)]+X′min(i)

(12)

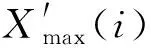
4.4 橋梁健康狀態下模型測試

確定CNN-LSTM神經網絡預測模型作為橋面系局部健康狀態識別模型超參數，對某大跨度鋼桁架橋BSHMS采集的橋面縱梁測點應變值進行預測，圖10為CNN-LSTM神經網絡預測模型的訓練結果。由圖10可知，模型對S1測點應變數據有很好地擬合效果。

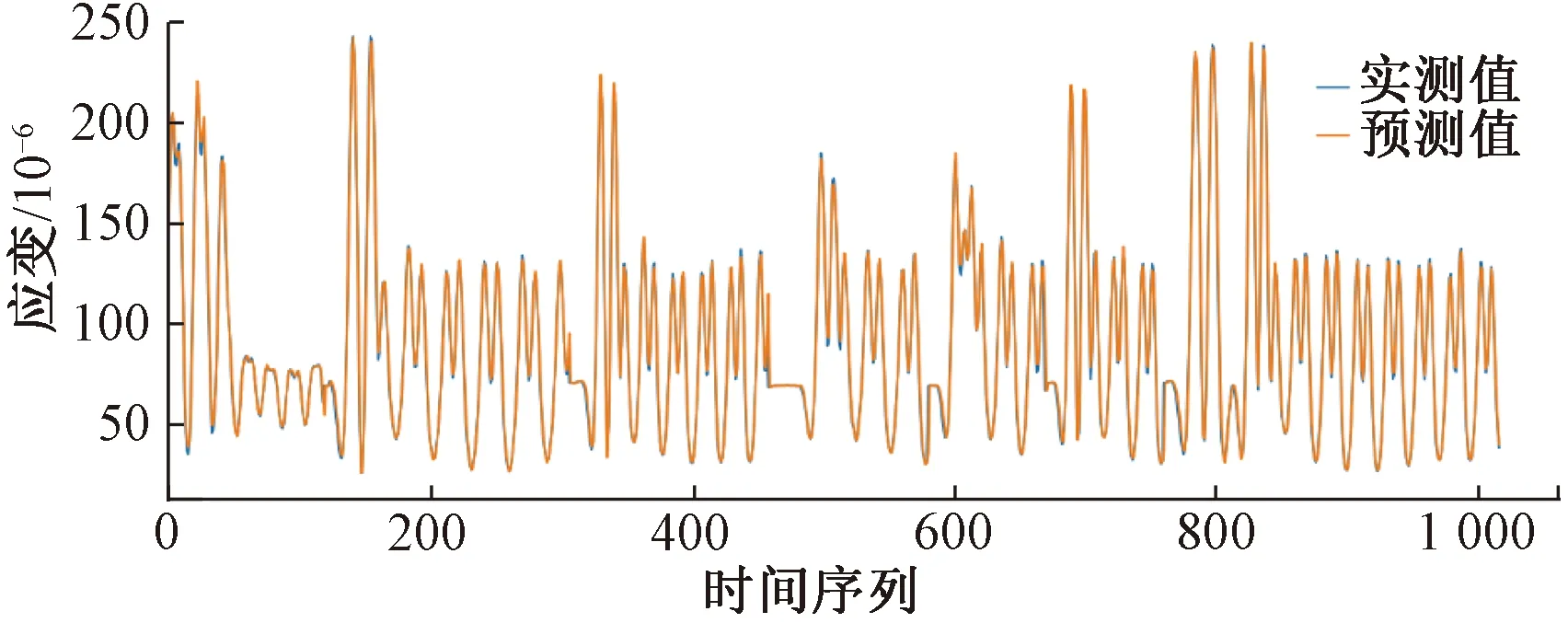
圖10 CNN-LSTM神經網絡模型預測結果

為更直觀地說明CNN-LSTM模型對大跨度桁架橋梁結構橋面系局部損傷預警的適用性，此處將模型的預測相對殘差數值進行可視化展示，結果見圖11。

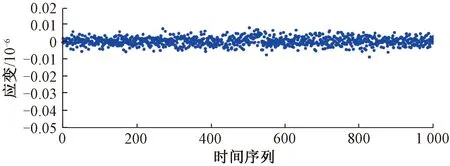
圖11 CNN-LSTM神經網絡模型預測相對殘差

從圖11可以看出，CNN-LSTM神經網絡預測模型相對殘差數值波動范圍介于[-0.01,0.01]，說明模型在橋梁橋面系局部損傷預警方面有著良好的適用性。

為驗證CNN-LSTM神經網絡預測模型與其他深度學習模型的優劣，將本文模型與RNN模型、CNN模型、LSTM模型在相同環境下，使用相同數據集進行對比試驗。考慮模型參數對試驗預測結果影響較大，試驗均采用交叉驗證的方式，對比經多次試驗得到的最佳預測模型，計算每種模型的MAE和RMSE，結果見表5。由表5可知，在相同環境下，本文模型相較于RNN、CNN、LSTM有良好的預測效果，優勢明顯。

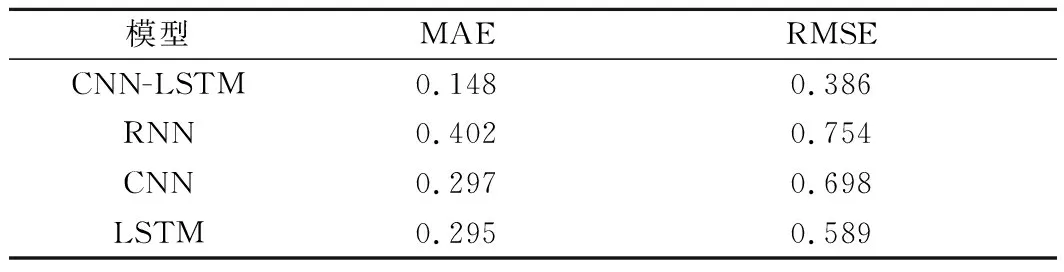
表5 不同模型預測結果對比

4.5 橋面系測試節間縱梁損傷狀態下模型測試

本文通過式(9)模擬該鋼桁架橋橋面系局部性能退化出現損傷，利用η表征橋梁損傷工況，本次試驗模擬將η設置為5%，將包含橋梁結構出現損傷時的監測數據作為數據集輸入至CNN-LSTM神經網絡預測模型中，將模型預測結果與橋梁健康狀態時設置的閾值控制線進行對比，對比結果見圖12。

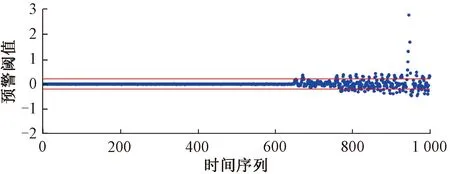
圖12 指數加權移動平均之后的相對殘差

由圖12可以看出，橋梁結構橋面系存在損傷時，采用CNN-LSTM模型進行預測，表明其殘差數值已超過橋面系處于健康狀態時所設置的閾值控制線，說明在橋梁結構出現橋面系局部損傷時，模型能夠實現損傷預警。

在實際識別時，可利用前述列車車型及荷載識別結果，對測試應變進行歸一化處理，即去除列車荷載變化導致的應變幅值變化，進而提高損傷預測識別的準確度。

5 結論

本文研究了大跨度鋼桁架橋上列車荷載識別與局部損傷預警問題，得出以下結論：

(1)在對比分析現有數據處理技術基礎上，使用EEMD方法提取了BSHMS中的車致應變數據，成功剔除了因溫致應變導致的橋梁結構響應相關性變化的影響。

(2)根據車致應變數據與車速信息計算出了列車荷載系數，進一步計算出了列車總體重量，通過某鋼桁架橋實測數據驗證了列車荷載系數的有效性。

(3)提出了基于CNN-LSTM的橋梁健康監測損傷預警模型，使用橋梁結構處于健康狀態時的監測數據，以提取的車致應變數據作為模型訓練的輸入量，作為CNN-LSTM模型的訓練數據，根據訓練后的模型預測結果殘差，使用EWMA控制圖來設置預警閾值，用于橋梁結構損傷識別。

(4)使用某鋼桁架橋健康監測系統中的實測數據集，對所提橋梁結構損傷預警模型進行試驗驗證；對比不同的預測方法，發現CNN-LSTM模型預測效果最好，能夠利用結構響應相關性進行應變預測。使用含橋梁結構損傷狀態的數據集對所提方法進行驗證，證明該模型能夠用于橋梁損傷預警。

本文在損傷識別預測中，主要考慮了列車荷載、應變和溫度在時空上的相關性，嘗試僅通過應變單一因素進行局部健康狀態評定和損傷識別的可行性，通過增加測試截面，可以擴展損傷識別的范圍，提高識別的效率，本文研究對BSHMS系統在列車荷載和損傷識別方面的應用具有參考意義。