曲線區段受電弓-接觸網系統建模及動態性能分析

熊嘉銘，徐 釗，魯小兵，劉志剛，宋 洋

(1.西南交通大學 國家軌道交通電氣化與自動化工程技術研究中心，四川 成都 610031；2.中鐵二院工程集團有限責任公司，四川 成都 610031；3.挪威科技大學 結構工程系，特隆赫姆 7491)

高速鐵路列車通過受電弓與接觸線之間的滑動接觸將電能從接觸網傳輸到機車。弓網間的動態性能不但直接決定受流質量，同時也影響弓網系統各部件的服役壽命和電氣化鐵路的安全可靠運行。隨著高速鐵路的不斷提速與運營里程的不斷增加，弓網動態性能的評估與優化受到越來越多研究者的關注。

接觸網建模通常采用非線性有限元方法[1-2]。其中，接觸線、承力索等線索可以等效為梁單元[3-4]或索單元[5]，定位器、線夾、腕臂、吊弦等部件則可通過與頻率相關的有限元法等效為單獨的質量塊或振動單元[6]。為保證施加了線索張力與結構自重的接觸網靜態位移符合規范，還需確定接觸網的初始平衡狀態[7-9]，常用方法有基于有限單元的分模法[10]、絕對節點坐標法(ANCF)[11-12]與負弛度法[13]。受電弓模型主要有兩類：歸算質量模型與多體模型。歸算質量模型的各項參數可通過頻率響應法計算得到[14-15]，通過該方法建立的受電弓模型可以保證在0～20 Hz頻率段的有效性[15]和0～350 Hz頻率段頻響特性的精確性[14]。受電弓多體模型可基于相對坐標系下的R/W方程建立，通常應用于受電弓的優化設計研究[16]。

評估弓網動態性能與受流質量的優劣，通常關注的指標包括弓網接觸壓力、導線動態高度及燃弧等[17]。其中接觸壓力作為重點研究對象，可通過建立弓網耦合動力學模型獲取[18-20]。分析接觸力在時域上的各項統計指標從而獲得接觸力的波動特性，是評價弓網動態性能的有效方法。接觸力產生波動內部因素主要有接觸線振動波傳播[21]和接觸線不平順[22]；外部激勵主要有風載荷[23-26]、空氣動力不穩定性[27]、機車激勵[28]和溫度變化[29]等。此外，采用頻域分析法對接觸線譜進行研究，計算接觸線不平順的波長成分及各波長的不平順幅值，以獲取弓網動態性能的頻域特性[30-32]。

現階段有關弓網動態性能的研究往往基于直線區段展開，對曲線區段弓網動態性能的研究較少。文獻[33]建立曲線區段簡單鏈型接觸網有限元模型與受電弓多體模型，通過車頂軌跡確定受電弓的位移，采用聯合仿真研究弓網系統的耦合動力學行為，證明曲線區段與直線區段的弓網動態性能存在差異。文獻[34-35]通過研究曲線區段線路參數、列車振動、施工維修誤差與接觸線風偏移等因素，給出不同曲率半徑線路下的拉出值設置范圍。然而，曲線區段接觸網導高以軌面坐標系定義，軌面的傾斜導致了接觸網在世界坐標系下并非垂直架設，其各組成部件的空間幾何位置均會發生改變。同時受電弓隨列車的側滾運動而傾斜，運動狀態從平直運行變成曲線傾斜運行，滑板、上框架與下框架的空間幾何位置也發生相應的改變。其中接觸網空間位置與受電弓運行狀態的改變還將導致受電弓與接觸線的耦合接觸方向從世界坐標系下的垂向方向轉化為傾斜軌面的垂向方向，這些變化必然會對弓網動態性能產生多方面的影響。

基于曲線區段弓網系統空間幾何位置與受電弓運行狀態的特殊性，本文對接觸網與受電弓的曲線特性進行數學解析。采用中國西南地區某高速鐵路客運專線彈性鏈形接觸網的設計參數與線路參數，建立接觸網與受電弓在曲線區段的動力學耦合模型。通過對受電弓簡化方案的可行性分析，證明弓網模型考慮曲線特性的必要性。基于所建模型，對不同曲率半徑、不同拉出值設置方式以及直、曲線線路下的弓網動態性能進行分析。

1 曲線區段弓網建模

本章主要介紹弓網系統有限元模型建立方法，以及曲線區段弓網系統的曲線特性及其數學解析過程，并采用EN 50318—2018[36]標準對接觸網建模方法的準確性進行驗證。

1.1 弓網建模及驗證

利用有限元分析軟件Ansys 建立弓網有限元模型。其中，接觸網模型采用三維梁單元Beam188模擬接觸線與承力索的空間非線性大變形，非線性彈簧單元Combin39模擬吊弦的抗拉特性，結構質量單元Mass21模擬線夾的集中質量特性。受電弓模型采用聯合彈簧滑動器與阻尼器的Combin40單元建立。接觸網結構約束包括：承力索座點處設置6自由度全約束；接觸線端部定位點處設置3自由度位移約束，保證整體接觸網結構的穩定；定位器底座處設置3自由度位移約束，保留腕臂的旋轉能力。基于非線性有限元求解，計算弓網動態性能。構建的三維接觸網模型如圖1所示。

圖1 三維接觸網有限元模型

為證明本文建立的弓網模型的準確性，采用EN 50318—2018中接觸網的靜態標準與動態標準對模型進行驗證。其中動態仿真選擇0.25 m里程對應的采樣步長與0～20 Hz接觸壓力濾波處理，并選取弓網接觸力穩定后的接觸力數據進行取值分析，以消除邊界不穩定跨的邊界效應影響。參考模型的結構與材料參數如圖2與表1所示，此外接觸網結構高度為1.8 m，吊弦間隔為9.17 m，吊弦數量為7個，跨距選取65 m，拉出值采用±300 mm，定位器長度為1.15 m。 表2為接觸網的靜態結果驗證，其中接觸線各點垂度誤差低于標準規定誤差(±5 mm)，恒定移動垂直力(200 N)下接觸線等效彈性誤差低于標準規定的誤差(±0.1 mm/N)，靜態結果滿足EN 50318—2018標準規定。表3給出了接觸網的動態結果驗證，可以看出各項動態結果同樣符合EN 50318—2018標準規定。由此認為本文使用的建模方法滿足EN 50318—2018標準要求，可以進一步用于曲線區段弓網系統的動態性能分析。

圖2 彈性鏈型接觸網結構示意

表1 接觸網參考模型基本參數

表2 靜態結果驗證

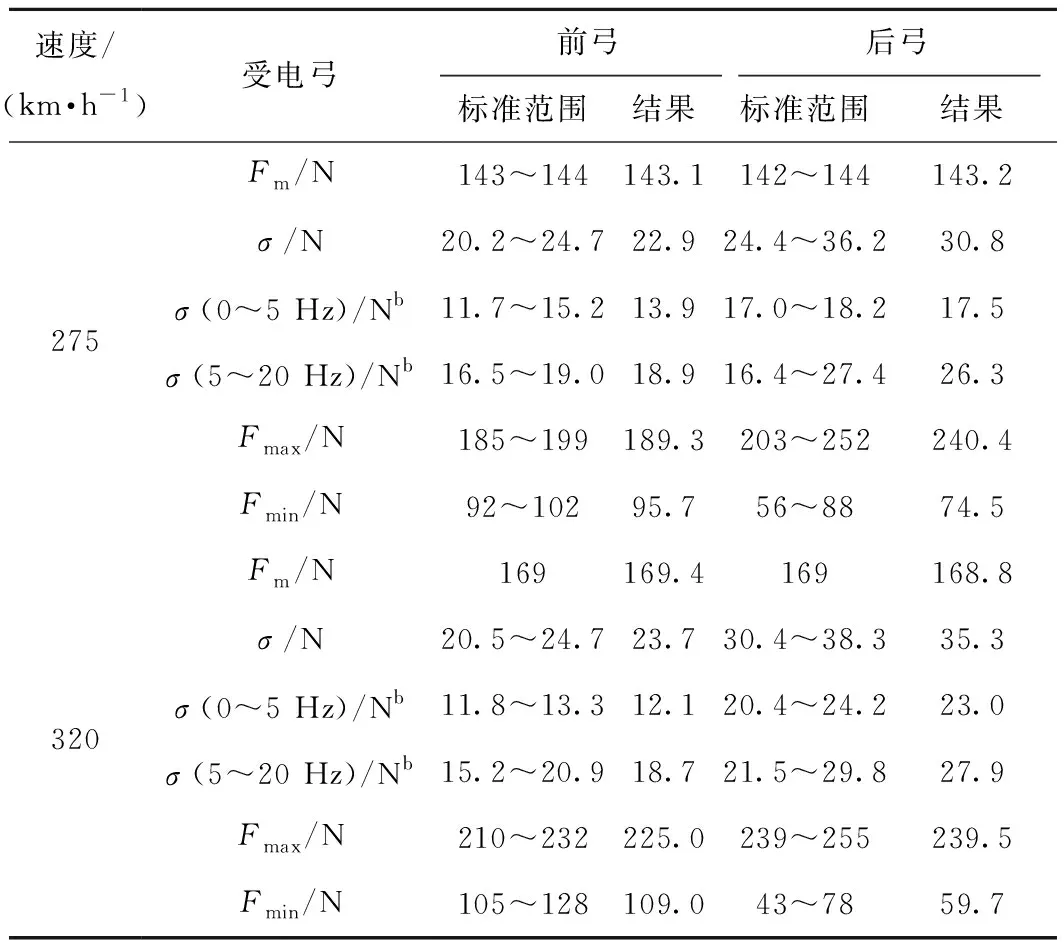
表3 動態結果驗證

1.2 弓網曲線特性

為了使列車安全通過曲線區段，軌道外軌有一定程度的超高，利用車體自重產生的轉矩來平衡所受到的離心力。外軌超高值的設置通常不超過125～150 mm，其導致的軌面傾斜即曲線區段弓網系統在動靜態特性上均區別于直線段的根本原因。相比于直線區段，弓網系統在曲線區段由于軌面傾斜而產生的特殊接觸網空間結構和受電弓運行狀態，本文稱之為弓網系統的曲線特性。

1.2.1 接觸網曲線特性數學解析

接觸網系統的曲線特性來自于確定接觸網導高的軌面坐標系發生傾斜后，接觸網在圖3所示的世界坐標系下的空間幾何位置產生了變化。值得注意的是，當相鄰定位點處接觸線的拉出值不相等時，為保證定位點至傾斜軌面的垂直距離為標準導高hcw不變，相鄰定位點間勢必會產生高度差，進而改變接觸網的結構特征，如圖4所示。

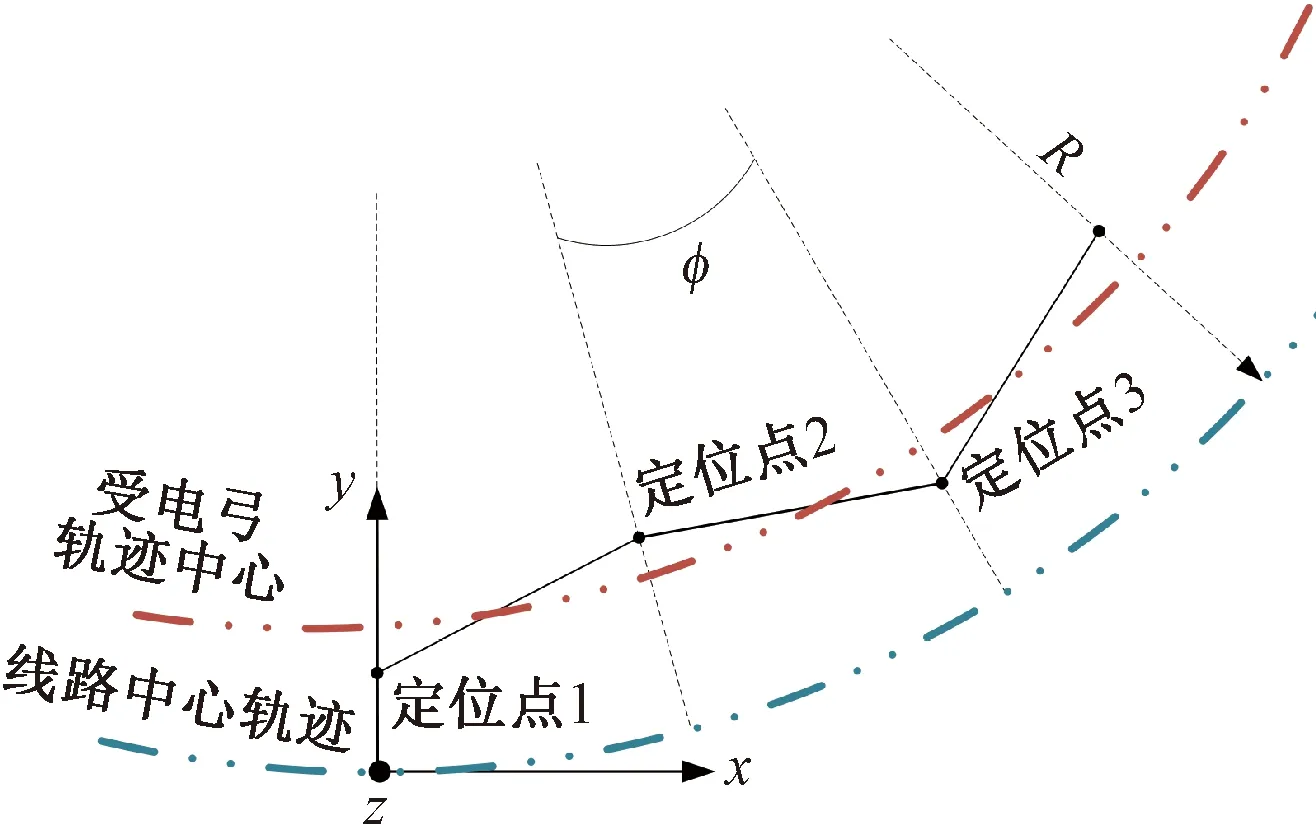
圖3 接觸網模型世界坐標系示意

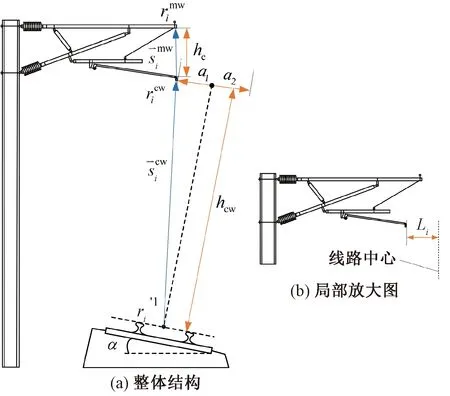
圖4 接觸網模型曲線特性示意

在圖3中定義世界坐標系坐標原點位于線路中心軌跡上，x軸沿線路切向方向，z軸沿線路法向方向，y軸沿地平面的垂直方向。線路中心軌跡方程可以表示為

x2+(z-R)2=R2

( 1 )

根據圖4，將第i個定位點所對應的軌道中心坐標向量表示為

( 2 )

( 3 )

式中：R為線路的曲率半徑；φ為當跨距為LA時對應弧長下的圓心角，可由余弦定理求得。

在考慮曲線特性對定位點空間位置的修正前，計算第i個定位點到對應線路中心之間的水平距離Li，用于輔助計算定位點的空間坐標。

Li=hcw×sinα-ai×cosα

( 4 )

式中：hcw為導高；ai為第i個定位點處設置的拉出值，取值如圖4中相鄰定位點拉出值a1或a2；Lc為標準軌距；α為軌道外軌超高導致的軌面傾斜角度，α=arcsin(h/Lc)。

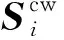
( 5 )

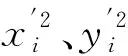
( 6 )

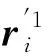
( 7 )

( 8 )

定位器與彈性吊索的空間位置可基于已確定的定位點和承力索座坐標遞推獲取。完成接觸網曲線特性的數學解析后，構建曲線區段的三維接觸網模型如圖5所示。

圖5 曲線區段接觸網有限元模型

1.2.2 受電弓曲線特性數學解析

受電弓的曲線特性來自于軌道外軌超高導致的列車傾斜進而帶動受電弓呈傾斜運行狀態，如圖6所示。此時受電弓中心相對線路中心產生了偏移，同時曲線區段受電弓整體也將保持一個固定的傾斜角度運行。對受電弓曲線特性的數學解析即確定受電弓中心的偏移量，得到計及該偏移量的靜態受電弓弓頭位置，完成受電弓初始位置的定位。受電弓的升弓過程與曲線傾斜運行過程可基于Ansys Apdl編程實現。

根據圖6，將受電弓所在位置對應的軌道中心坐標表示為

( 9 )

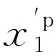
(10)

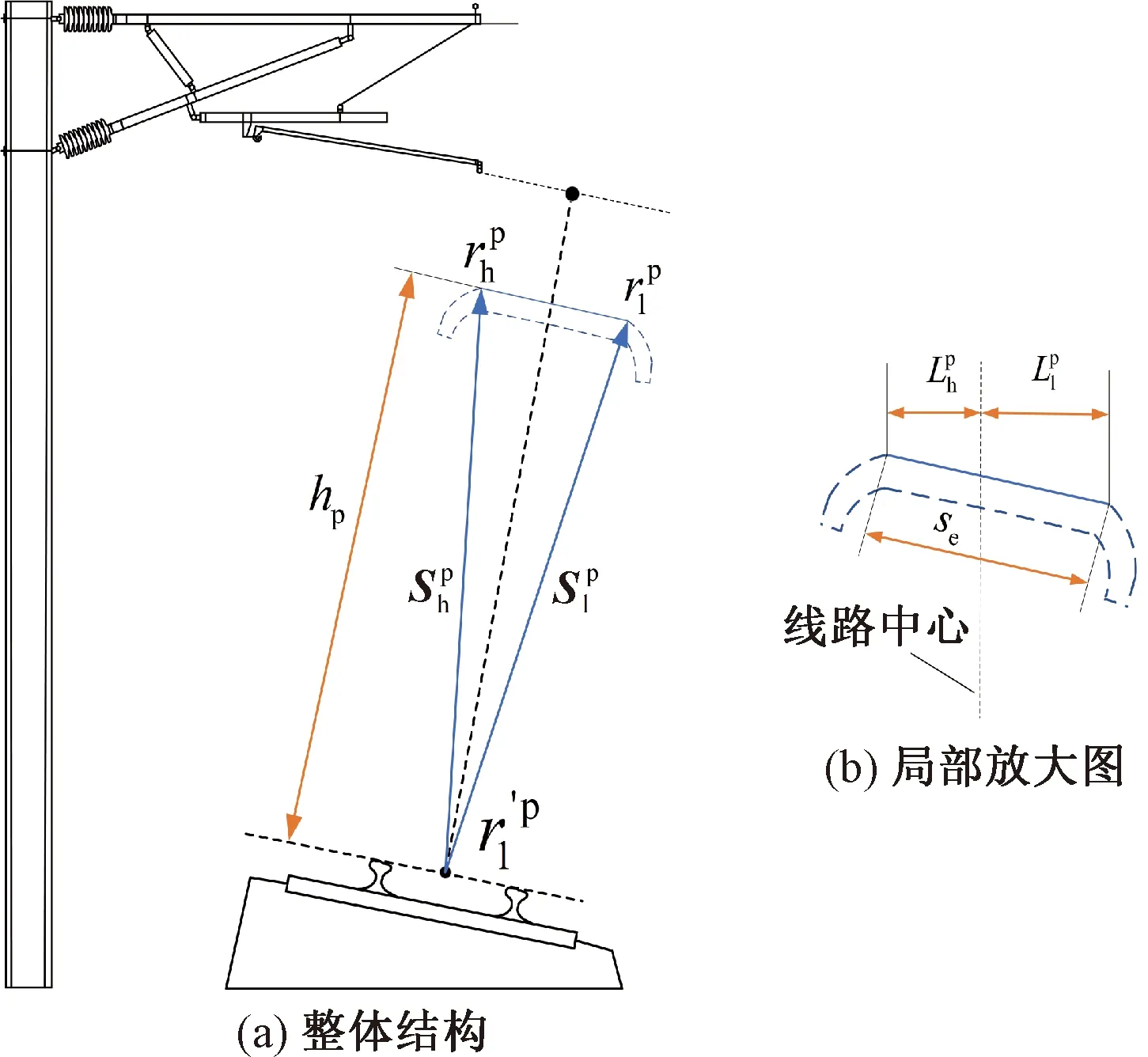
圖6 受電弓模型曲線特性示意

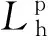
(11)

式中：hp為靜態受電弓滑板至軌面的垂直距離；se為受電弓弓頭的工作長度。

(12)

(13)

其中

(14)

(15)

得到受電弓滑板兩端端點的空間坐標為

(16)

(17)

受電弓模型中其他關鍵點的空間位置均可采用同樣方法求得。

2 算例的設置

采用第1章建模方法，建立曲線區段彈性鏈型接觸網和三元歸算質量受電弓模型，并設置多組算例研究曲線區段弓網系統動態特性，算例中弓網模型的基本參數見表4，此外接觸網結構高度為1.8 m，吊弦間隔為9.17 m，吊弦數量為7個，跨距選取65 m，拉出值采用±300 mm，定位器長度為1.15 m。算例間的差異性參數見表5。受電弓、接觸網和軌道參數均來自中國西南地區某高速鐵路客運專線，不同曲率半徑線路下接觸線的拉出值設置參考文獻[33-35]。

表4 弓網模型基本參數

表5 算例設置

3 曲線區段受電弓建模

如圖7所示，直線區段的受電弓呈平直狀態運行，而曲線區段的受電弓呈傾斜曲線運行狀態。考慮接觸線建模采用圓截面的Timoshenko梁單元，且受電弓模型對位移與力的響應始終沿滑板的法向方向，故兩種受電弓運行狀態只改變了受電弓滑板與接觸線之間的接觸方向，弓網耦合接觸行為的本質并沒有發生改變。基于Ansys仿真分析，相比于傾斜曲線運行狀態，直線狀態的受電弓模型在仿真中需要更少的節點自由度約束與位移約束。采用平直狀態的受電弓模型進行曲線區段弓網仿真的方案，可以降低計算難度與時間。本章驗證該方案是否能保證仿真結果的準確性。

圖7 弓網接觸示意

采用R3 000-AS、R5 000-AS和R7 000-AS三組算例，分別設置兩組受電弓模型，一組模型考慮曲線特性，另一組模型忽略曲線特性。如圖8所示，選取弓網接觸力穩定后的四跨接觸力數據進行取值分析，結果見表6。分析表6結果可知，采用忽略曲線特性的受電弓模型對弓網接觸力的平均值沒有產生顯著的影響，但明顯增大了接觸力的標準差，在R3 000、R5 500和R7000三組算例下接觸力標準差分別增加了9.02%、6.7%和7.0%，導致接觸力的波動變得更劇烈。

圖8 接觸力分析取值區段

對該現象產生的原因進行分析，通過圖7可知，在曲線區段，受電弓局部坐標系下的接觸線垂向靜態位移并非傳統世界坐標系下的垂向靜態位移，而是世界坐標系下的接觸線垂向靜態位移向弓網接觸方向轉化

表6 不同受電弓模型下的動態性能指標 N

后的結果。為分析受電弓在實際運行過程中受到的來自接觸線垂向靜態位移的影響，定義受電弓局部坐標系下接觸線垂向靜態位移為Zp，為計算方便，取在定位點處Zp的初始值為0 m時受電弓滑板運動軌跡面作為基準，Zp即為線路上受電弓滑板到接觸線的實際靜態距離。三組算例中接觸線的兩跨Zp曲線如圖9所示。

圖9 不同受電弓模型下Zp曲線對比

由圖9可知，當受電弓模型忽略曲線特性時，其Zp曲線的波動更加劇烈，且波動周期也從單跨長度50 m增加到雙跨長度100 m。

結合接觸網結構特性，由于相鄰定位點之間的高度差值遠大于接觸線垂向靜態位移，此時Zp被定位點高度差主導，從而導致動態性能的惡化。以曲率半徑為3 000 m的算例為例，對Zp曲線和弓網接觸力進行頻譜分析，如圖10所示。當受電弓模型考慮曲線特性時，Zp成分與接觸力成分在低頻段具有良好的對應關系，與文獻[37]所得結論一致，且Zp成分的最大峰值對應頻率為0.76 Hz，對應波長51.11 m，約等于實際跨距50 m。而當受電弓忽略曲線特性時，Zp成分的最大峰值對應頻率為0.38 Hz，對應波長102.48 m，約等于實際跨距的兩倍(即定位點高度變化周期100 m)，且此時Zp成分與接觸力成分并未保持對應關系，同樣的分析結果也出現在R5 000-AS和R7 000-AS兩組算例上。結果表明忽略曲線特性的受電弓建模方法會導致Zp值被相鄰定位點的高度差主導，弓網靜態距離對接觸力的影響被屏蔽，為保證仿真結果的準確性，該方案不可取，同時也證明了曲線區段弓網模型考慮曲線特性的必要性。

圖10 R3 000m線路不同受電弓模型動態仿真的弓網接觸力與Zp頻譜分析

4 曲線區段弓網動態性能

采用計及曲線特性的弓網模型，分析曲線區段拉出值設置和直、曲線路對弓網動態性能的影響。

4.1 拉出值設置對弓網動態性能影響

曲線區段拉出值的設置不僅影響定位點的空間位置坐標，還會對接觸網結構產生影響。當拉出值a1與a2相等時，相鄰定位點在豎直方向上等高；當拉出值a1與a2不等時，相鄰定位點存在高度差。實際接觸網設計與應用中，定位器通常在小曲率半徑線路上采用單向安裝而在大曲率半徑線路上采用正反交錯安裝，但為全面對拉出值設置方式對弓網動態性能的影響進行研究，因此對每組算例均設置兩種安裝方式。

對表5所列算例結果進行分析，接觸壓力標準差如圖11所示。由圖11可知，拉出值的設置方式影響弓網動態性能，當拉出值恒定設置時，弓網接觸力標準差更小；拉出值恒定設置后，改變該定值的大小不會對接觸力標準差產生影響。

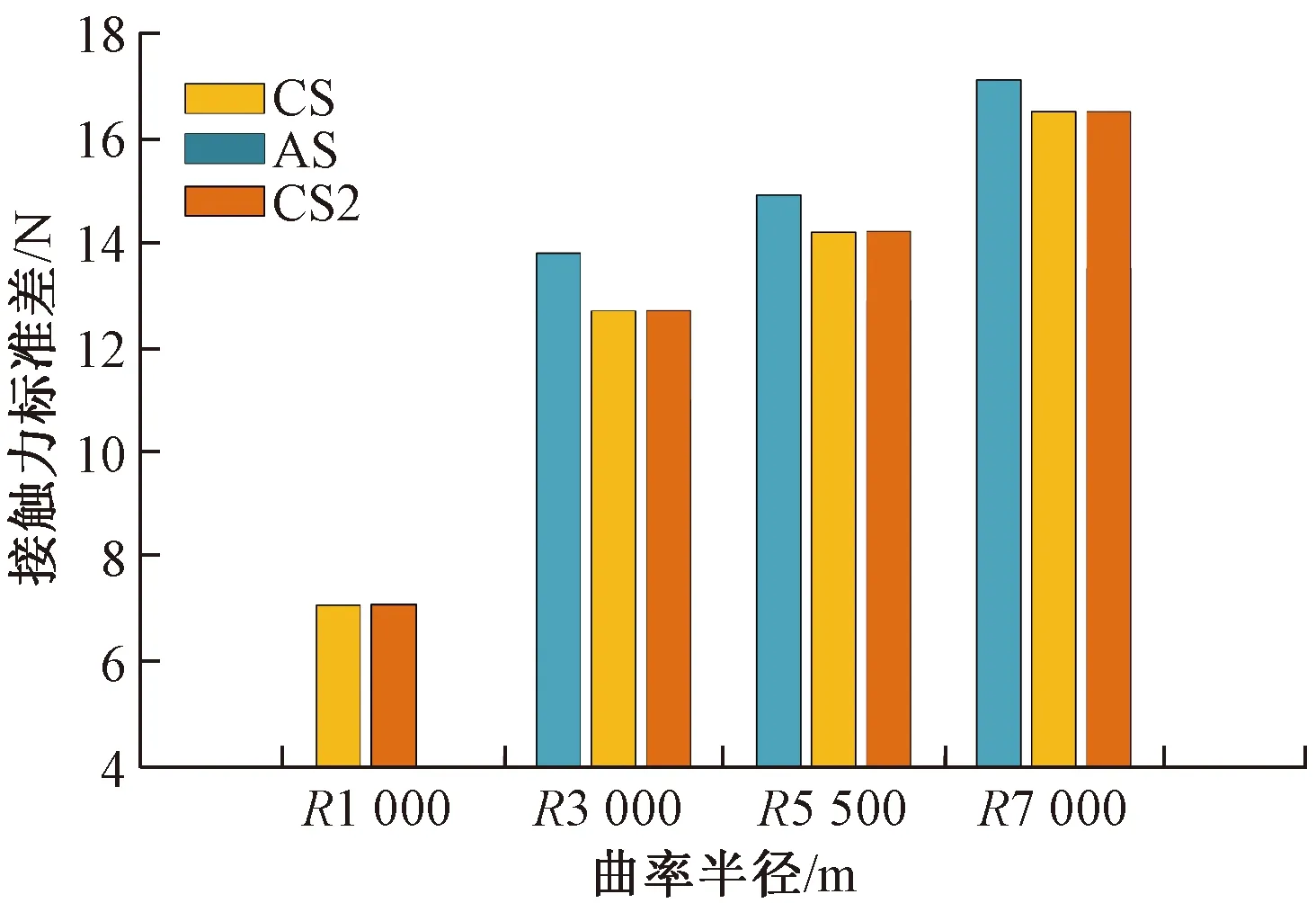
圖11 不同拉出值設置下接觸力標準差對比

拉出值的設置同時也對受電弓滑板上接觸點的運動范圍產生影響。過小的接觸點運動范圍會引起受電弓的偏磨現象，而過大的接觸點運動范圍則會引起受電弓的刮弓現象。因此在分析曲線區段拉出值設置對弓網動態性能影響的同時，應兼顧拉出值設置對接觸點運動范圍的影響，保證在允許的接觸點運動范圍內使受電弓滑板的磨耗更加均勻。受電弓滑板的磨耗區域如圖12所示，其磨耗區間的大小取決于定位點處或跨中處的接觸線空間位置。各算例中滑板磨耗區間見表7。

圖12 受電弓滑板磨耗區域示意圖

表7 不同拉出值設置下滑板磨耗區域對比

由上述可知：

(1)由于線路軌跡為曲線，即使將拉出值設置成定值，受電弓滑板上的接觸點仍存在往復運動范圍。

(2)拉出值恒定設置下的滑板磨耗區間更小，導致受電弓滑板的局部磨耗更嚴重，降低其服役壽命。

綜上所述，在曲線區段設計接觸線拉出值時，較好弓網動態性能與較大受電弓滑板磨耗區間不能同時兼顧，應根據首要設計需求與實際情況綜合考慮。

4.2 直、曲線區段弓網動態性能對比

建立直線區段弓網模型，采用與曲線區段弓網模型相同的材料參數，并在該模型下使受電弓分別以各曲率半徑線路的允許通過最大速度運行，進行直、曲線區段弓網動態性能的對比研究。由圖13可知，相同條件下曲線區段的弓網接觸力標準差更大，其中曲率半徑最小的R1 000-CS算例的接觸力標準差相比直線算例增加了19.3%，曲率半徑最大的R7 000-AS和R7 000-CS算例的接觸力標準差相比直線算例分別增加了18.4%和16.6%，證明基于直線區段的弓網動態性能測試并不能保證曲線區段弓網動態性能也滿足標準要求。

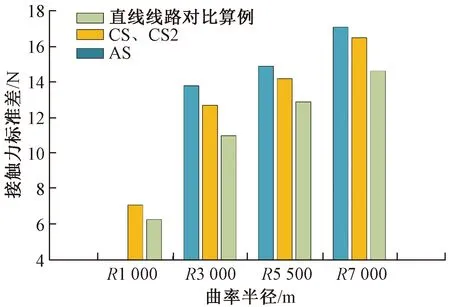
圖13 直、曲線路接觸力標準差對比

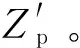
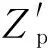
(2)曲線區段Zp曲線的波動遠大于直線區段的Zp曲線，即接觸線在受電弓局部坐標系下的垂向靜態位移大于其在世界坐標系下的垂向靜態位移，導致接觸力波動更加劇烈。

圖14 直、曲線區段曲線對比

4.3 曲線區段弓網接觸力頻譜分析

引起接觸力波動的原因主要有4類：

(1)接觸網剛度分布引起的接觸力波動。

(2)外部環境對弓網的激勵，如環境風和覆冰等。

(3)接觸線由于長期使用過程中的機械磨損和維護過程的不規范導致的表面不平順現象。

(4)接觸線上振動波的傳遞。

弓網動態性能惡化的主要原因為第一類，在基于直線區段弓網接觸力的頻譜分析中，大多接觸力成分直接來自于接觸網周期性結構參數，但基于曲線區段的接觸力分量在低頻段與高頻段的分布仍然值得探討。本節針對3個算例進行曲線區段弓網接觸力的頻域特性分析。

(1)R1 000-CS

本算例中列車以75 km/h的速度在曲率半徑為1 000 m的線路軌道上運行，接觸力頻譜分析如圖15(a)所示。圖中，SPF表示跨距通過頻率，HSPF表示半跨距通過頻率，ZpPF表示Zp曲線通過頻率，SDPF表示定位點到吊弦通過頻率，DDPF表示吊弦到吊弦通過頻率，可以看出接觸力的低頻成分占主導地位，其中在頻率0.41 Hz處為最大峰值，對應波長為51.2 m，約等于實際跨距50 m。對主要峰值進行比較，除頻率為1.22 Hz處的接觸力成分是由Zp分量引起的，其他幅值較大的接觸力成分均可以找到對應的接觸網周期性結構。

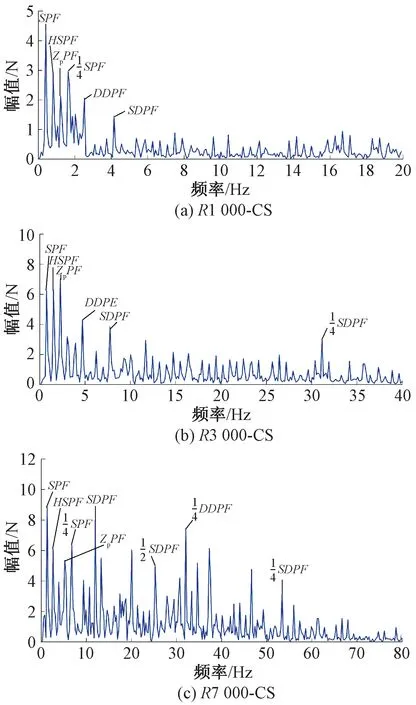
圖15 接觸力成分頻域分析

(2)R3 000-AS

本算例中列車以140 km/h速度在曲率半徑為3 000 m的線路軌道上運行，接觸力頻譜分析如圖15(b)所示。可以看出接觸力的低頻成分仍占據較大的比重，但在頻率為31.14 Hz處出現了一個可明顯辨識的分量，對應波長為1.25 m，等于四分之一定位點到吊弦的距離1.25 m。

(3)R7 000-AS

本算例中列車以240 km/h的速度在曲率半徑為7 000 m的線路軌道上運行，接觸力頻譜分析如圖15(c)所示。隨著速度的進一步提高，可以看到接觸力的高頻成分顯著增大。同時在高頻段可辨識到頻率為25.26、32.03和53.39 Hz的3個接觸力分量，其對應波長分別為2.63、2.08和1.25 m，約等于二分之一定位點到吊弦的距離2.5 m、四分之一吊弦到吊弦的距離2 m和四分之一定位點到吊弦的距離1.25 m。同時在高頻段出現了部分未能與接觸網周期性結構和Zp對應的接觸力分量。

通過對算例的分析可知：

(1)在曲線區段，隨著列車運行速度的增加，接觸力成分在高頻段的能量變大，較短的結構參數如吊弦間距/定位點-吊弦間距的二分之一和四分之一對接觸力的影響加劇，這與文獻[38]中基于直線線路上的研究結果一致，證明接觸力高頻成分對接觸力整體的影響不可忽視。

(2)在曲線區段，全頻率段均出現了部分未能與接觸網周期性結構和Zp對應的接觸力成分，使接觸力成分變得更加復雜

5 結論

本文介紹接觸網和受電弓曲線區段建模過程，采用EN 50318標準對建模方法的有效性進行驗證。通過對不同受電弓建模方案的可行性分析，發現采用忽略曲線特性的受電弓模型會導致Zp曲線波動變大，仿真結果失真，證明了曲線工況下弓網模型計及曲線特性的必要性。利用所建模型對曲線區段弓網的動態性進行研究，得到如下結論：

(1)在曲線區段，將接觸線拉出值設置成恒定值有利于弓網獲得更好的動態性能。當拉出值恒定設置后，拉出值的大小并不會對弓網動態性能產生明顯影響，但該拉出值設置方式會明顯減小受電弓的磨耗區域，加重受電弓的偏磨現象。

(2)由于接觸線在世界坐標系下的垂向靜態位移向受電弓局部坐標系轉化的過程中變化幅度增大，導致曲線區段弓網的接觸力標準差相較于直線區段上有所增大，動態性能出現了惡化。

(3)隨著列車運行速度的增加，曲線區段弓網接觸力高頻成分能量顯著增大，較短的接觸網周期性結構參數對接觸力分量的影響加劇，高頻段的接觸力分量不可忽略。傳統評估標準中的0～20 Hz低頻接觸力指標難以全面反映曲線區段弓網的動態性能。同時，全頻率段出現了小部分未能與接觸網周期性結構和Zp對應的接觸力分量，使接觸力成分更加復雜。

研究結果表明，曲線區段的弓網系統在靜態結構和動態性能兩個方面均與在直線區段上有明顯差距。未來的弓網設計與標準制定中，應增加對曲線工況的考慮。