關于Arrhenius公式的幾點討論

張晨曦，蘇涵，張樹永

山東大學化學與化工學院，濟南 250100

Arrhenius公式于1889年由實驗結果得出，是最重要的化學動力學經驗公式，是支撐化學動力學理論發展的兩大實驗基礎之一，其所建立的活化能概念更是影響深遠。但一百多年來，對該公式的討論從未停止，主要集中在以下幾個方面：(1) 能否從熱力學公式(如van’t Hoff方程)導出Arrhenius公式？(2) 活化能的定義及物理意義到底是什么？(3) Arrhenius公式適用的溫度范圍及其修正；(4) Arrhenius公式和與之形式類似的公式(如van’t Hoff方程等)是否存在內在聯系？

本文追溯了Arrhenius公式產生的歷史過程，指出了當前討論中存在的一些問題，提出了改進的意見和建議。這些討論有利于糾正一些錯誤認識，使讀者正確理解和應用Arrhenius公式。

1 Arrhenius公式的提出

1884年，van’t Hoff首先得到速率公式(1)，并延伸得到公式(2)[1]：

其中，T為絕對溫度，k為速率常數，q為在恒定體積下過程的熱效應，A、B為經驗常數。van’t Hoff從反應分子數出發，研究了多個單分子及多分子反應，得到了k與T的經驗關系，并發現這些經驗關系存在較大差異，在其整理的8個反應的k-T關系中，只有氯乙酸水溶液的分解反應在80-130 °C的溫度范圍內具有與后來的Arrhenius公式相似的形式。故van’t Hoff指出“我將不強調經驗和經驗結果的一致性，而強調從目前的經驗中可以得出的一般結論，即：溫度對轉化速度的影響隨所考慮的反應而變化。”van’t Hoff選擇尊重實驗事實，他的結論是：針對不同的反應，式(2)中的常數A可以為零，而B可以不為零。他沒有明確常數A、B的物理意義，并認為該式不具有普遍適用性[2]。

1889年Arrhenius得出速率r和溫度T的關系式為：

其中A是常數，T0、T1是絕對溫度，是不同溫度下的反應速率。他給出了7個實驗的數據，證明了上述公式成立。結合van’t Hoff速率方程(式2)，他引入假設，以蔗糖水解反應為例，指出反應速率和“活性蔗糖”的量成比例，且在恒溫下可以近似認為“活性蔗糖”的量與“非活性蔗糖”的量成比例。此時有：

這兩個公式后來都被稱為Arrhenius公式，式(4)是其微分形式，式(5)是其積分形式。Arrhenius賦予q活化能的概念，并給出了活化能的物理意義：反應物分子轉變為活化分子所需的能量。顯然，相較于van’t Hoff最初提出的動力學公式，Arrhenius舍去了常數B，并賦予了van’t Hoff速率公式A以明確的物理意義，使該公式具有了普遍使用的合理性[3]。

追溯歷史，Arrhenius是基于實驗事實得出公式(4)和(5)的，并非從van’t Hoff方程導出或類比得到的。而van’t Hoff則是先得出類似Arrhenius公式的動力學方程(式2)，進而導出了熱力學關系。現在一直有人試圖從熱力學的van’t Hoff方程導出動力學的Arrhenius公式。不難發現，在該推導過程中，出現了“想當然”的對應關系，即將活化能Ea與反應物或者生成物的標準摩爾生成吉布斯自由能之和對應[4]：

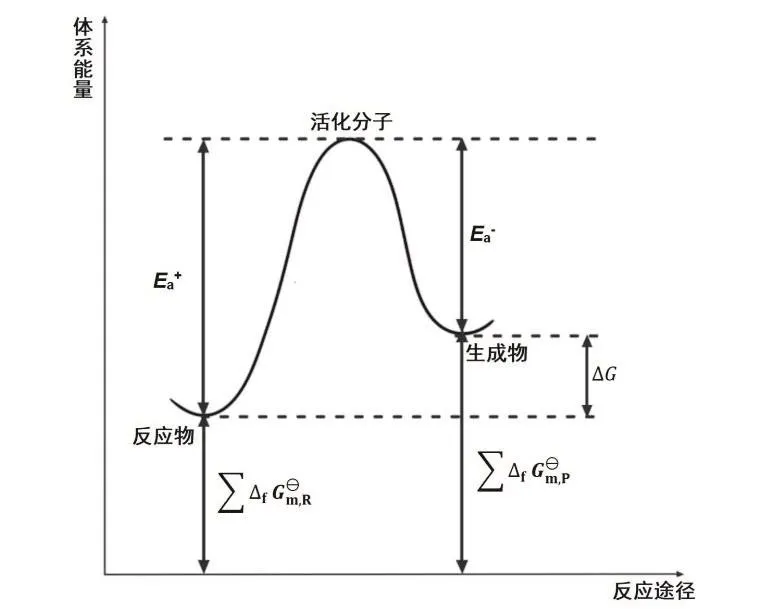
圖1 標準狀態下化學反應體系自由能變化與體系狀態的關系圖

從哲學角度而言，運動是絕對的，靜止是相對的，van’t Hoff方程所對應的平衡狀態，實際上是一個特殊的運動狀態(正逆反應速率相等)，故從動力學速率相等導出熱力學平衡關系是可行的，反之則不然。

2 活化能的物理含義

1996年，IUPAC推薦的活化能定義是Arrhenius圖(lnk-1/T圖)中直(曲)線在溫度T下的斜率[5]。該值來源于實驗，故稱實驗活化能(experimental activation energy)。與具有明確定義和物理意義的其他物理量不同，反應的活化能存在多種解釋。不考慮簡單碰撞理論、過渡態理論和光化學等對活化能的不同理解，人們給出的活化能定義主要有以下三種[6]：

(1) Arrhenius (1889)：反應物分子轉變為活化分子所需的能量。

(2) Lewis (1918)：活化分子能量的最低值與反應物分子平均能量之差。

(3) Tolman (1925)：活化分子平均能量與反應物分子平均能量之差。

Arrhenius指出，只有能量足夠高的分子才能發生反應，而達到反應所需能量的分子稱為活化分子。對于單分子反應而言，活化分子的概念容易理解，但對于多分子反應卻存在歧義。以A + B → C反應為例，是A、B分子都必須達到活化狀態才能發生反應？還是A分子和B分子整體達到反應所需的能量就能發生反應？如果是后者，則發生反應的A、B分子不需要都成為活化分子，此時的活化分子和活化能的物理意義不再明確。

從目前普遍接受的Tolman定義來看，Tolman首先從單分子基元反應出發，基于簡單碰撞理論，在宏觀非快速、服從Boltzmann分布的氣相或稀溶液條件下，結合化學動力學和統計力學導出：

對于雙分子反應而言，Tolman提出了兩種機制，其一是A、B兩種分子均達到活化狀態然后碰撞發生反應，即將活化和反應分開；其二是未被活化的A、B分子碰撞的能量超過了平均動量直接反應，此時活化和反應過程融合[7]。兩種機制下的Ea具有截然不同的物理意義。第一種情況下：

即雙分子反應活化能為兩種活化分子的平均能量與所有分子的平均能量之差，滿足式(8)的定義，但不符合簡單碰撞理論模型。在簡單碰撞理論中，只要分子碰撞的相對平動能在質心連心線上的分量超過某一閾值即可反應，并不要求兩種分子都達到活化狀態。

在第二種情況下，每個分子都活化不是反應的絕對前提，只要A、B兩種分子的碰撞速率達到某一臨界值或者整體動量達到某一閾值，即可直接反應。這種機制滿足簡單碰撞理論模型也相對合理，但不再符合Tolman對活化能物理意義的解釋。在此，我們借鑒溶液化學“遭遇對(encounter pair)”的概念，引入“活化分子對(activated molecule pair)”或者“反應分子對(reactive molecule pair)”概念，指代可以發生反應的一對或者一組分子。根據統計熱力學原理，假設“活化分子對”的數量比例依然滿足Boltzmann分布，則類比單分子反應活化能的物理意義，可以得出多分子反應活化能的表達式為：

因此，我們建議拓展Tolman定義中的“活化分子”概念，將活化能定義為：活化分子或活化對的平均能量與反應物分子或反應物分子對平均能量之差。其中，活化分子對應單分子反應，活化對對應多分子反應。需要說明的是，修改后的定義雖然更加合理也更加符合實際，但由于活化對中每個分子的能量并不確定，故無法使用Boltzmann分布說明其各自所占的比例。

3 Arrhenius公式的溫度適用范圍

作為最基本的動力學公式，Arrhenius公式應用領域雖然廣泛，但僅適用于五類k-T關系中的第一類和第五類，對第二到第四類并不適用[8]。但即使是第一類和第五類反應，其使用的溫度范圍也是有限的。隨著實驗技術的發展以及應用領域的拓展，人們發現Arrhenius公式的lnk與1/T的線性關系只在某個溫度范圍內能夠保持，一旦超出該溫度范圍，則線性變差，此時需要對Arrhenius公式進行修正。

1955年Hyne和Robertson結合Everett和Wynne-Jones提出的平衡常數與溫度的三常數公式[9]提出了動力學三常數Arrhenius修正公式：

A、B、C都是與溫度無關的常數[10]。早在1893年Kooij曾提出相似形式的公式[11]，因不夠簡潔、物理意義不明確而未普遍使用。隨著動力學的發展，該修正公式各參數被賦予了明確的物理意義，并變為以下形式：

其中，A和Ee都是與溫度無關的常數，m為實數[12]。經過校正后，Arrhenius公式的適用溫度范圍可以大幅度提升。

目前，雖然多數教材都強調了二常數Arrhenius公式應用的溫度限制，卻并未明確指出公式適用的溫度范圍。在此，我們基于式(12)，通過定量計算說明Arrhenius公式對常見反應的適用溫度范圍。

對式(12)取對數后微分

可以證明，此時反應的活化能符合：

與式(2)比較可知，式(2)中的常數A與能量項(Ee)有關，而B則與活化能隨溫度的變化程度m有關。如果m = 0，則lnk與1/T在任何溫度范圍內都符合線性。但實際上，幾乎沒有反應的lnk與1/T的關系能夠在如此廣泛的溫度范圍內保持線性，這說明m通常并不為零。隨著溫度的升高，mRT的影響逐步加大，導致溫度對活化能的影響不能再被忽略時，即會導致lnk與1/T的關系偏離直線。需要說明的是，對于預測電子材料使用壽命等對溫度要求比較嚴苛的精密技術領域，這種微小偏差也可能導致比較嚴重的問題。

化學反應的活化能通常在40-400 kJ·mol?1，活化能小于80 kJ·mol?1的為快反應，活化能超過120 kJ·mol?1為慢反應，這兩類反應通常很難研究，故人們研究的常見反應的活化能通常在80-120 kJ·mol?1的范圍內。為了直觀地體現m和T的變化對活化能的影響，我們取Ee為80 kJ·mol?1，m= 0-10，T= 273.15-1073.15 K，將三常數公式(式13)計算值看作真實值，分別利用三常數公式(式13)和二常數公式(式15)作圖所得斜率分別求出對應的活化能示于圖2。

圖2 Ea (三常數)和Ea (二常數)與1/T和m的三維關系圖

二常數公式：

圖2是首次報道，可用于判斷二常數Arrhenius公式在不同m和T下的溫度適用范圍。

其顯示，當溫度較低、m值較小時，使用三常數和二常數公式所得的Ea是重疊的。通常，在溫度變化不大、分子結構比較簡單、不考慮振動影響時，m通常不大于4[13]。如果取m= 0.5，則在室溫(293.15 K)下，mRT的數值只有1.22 kJ·mol?1，只占正常活化能的1.0%左右，可以忽略其影響。這是Arrhenius公式能夠成為普適性公式的前提。

在實驗測量活化能時，人們通常從比室溫略高的溫度(如298.15 K)開始，以10 °C為間隔，在25、35、45、55、65 °C測量5個以上的點，前后的溫差有40 °C。如果實驗的溫度測量精度可以達到0.1-0.01 °C，溫度測量的相對誤差在±(0.1%-1%)，則對于Ee為80 kJ·mol?1的反應，在上述溫差范圍內活化能改變±1%所對應的m值為6.0 (見表1)。

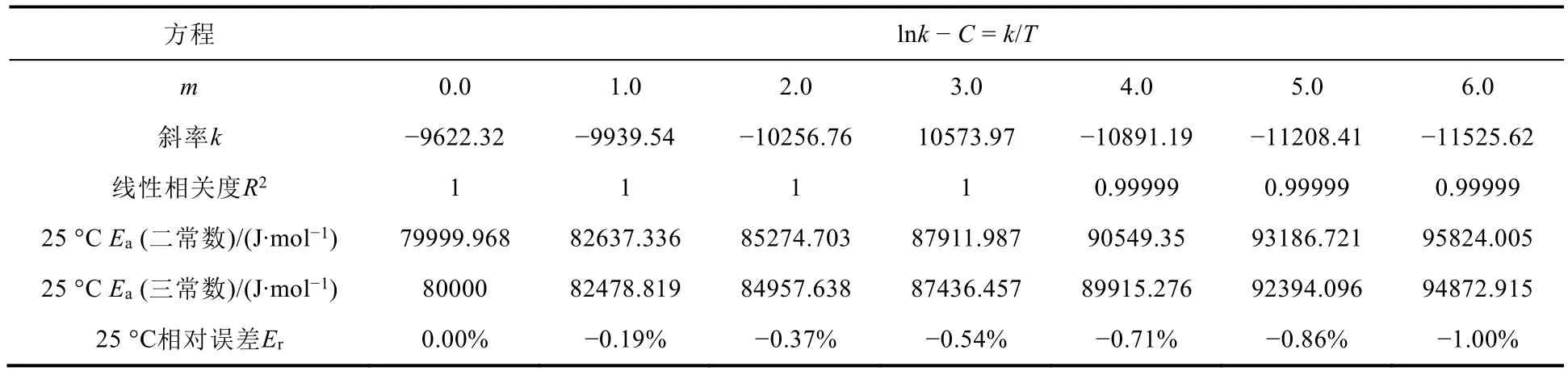
表1 Arrhenius曲線圖相關數據

由表1可以看出，活化能改變?1%時，線性相關系數依然很好，這說明線性并不能用于判斷Arrhenius公式是否適用。

圖2顯示，隨著溫度的升高和m值的增加，依據二常數和三常數公式所得活化能出現明顯的差異。這說明，對于復雜分子、超過40 °C的溫差或者對活化能測量要求較高時，應采用三常數公式進行擬合。

4 公式形式相似的必然性

在物理化學教學過程中，人們發現van’t Hoff公式等多個熱力學公式具有與Arrhenius公式相似的形式，但參數的物理意義和使用條件卻截然不同。之前已有不少作者對該現象進行了歸納和分析，但一方面歸納不全面，另一方面沒有對出現相似性的本質給出解釋。在此，我們總結了物理化學教材最常出現的與Arrhenius公式形式相似的公式(見表2)，并對導致其相似性的本質特征進行了說明。

從表2不難發現，這些形式相似的公式所描述的都是對峙的化學或物理過程達到平衡的狀態。故一般的規律可以概括為：只要一個過程存在正向和逆向兩個相反過程，且其正逆過程的變化速率均符合質量作用定律，且平衡時滿足平衡常數等于正逆向過程的速率常數之比，即K=k+/k?，則描述該平衡狀態性質的熱力學公式一定具有與Arrhenius公式相似的形式。

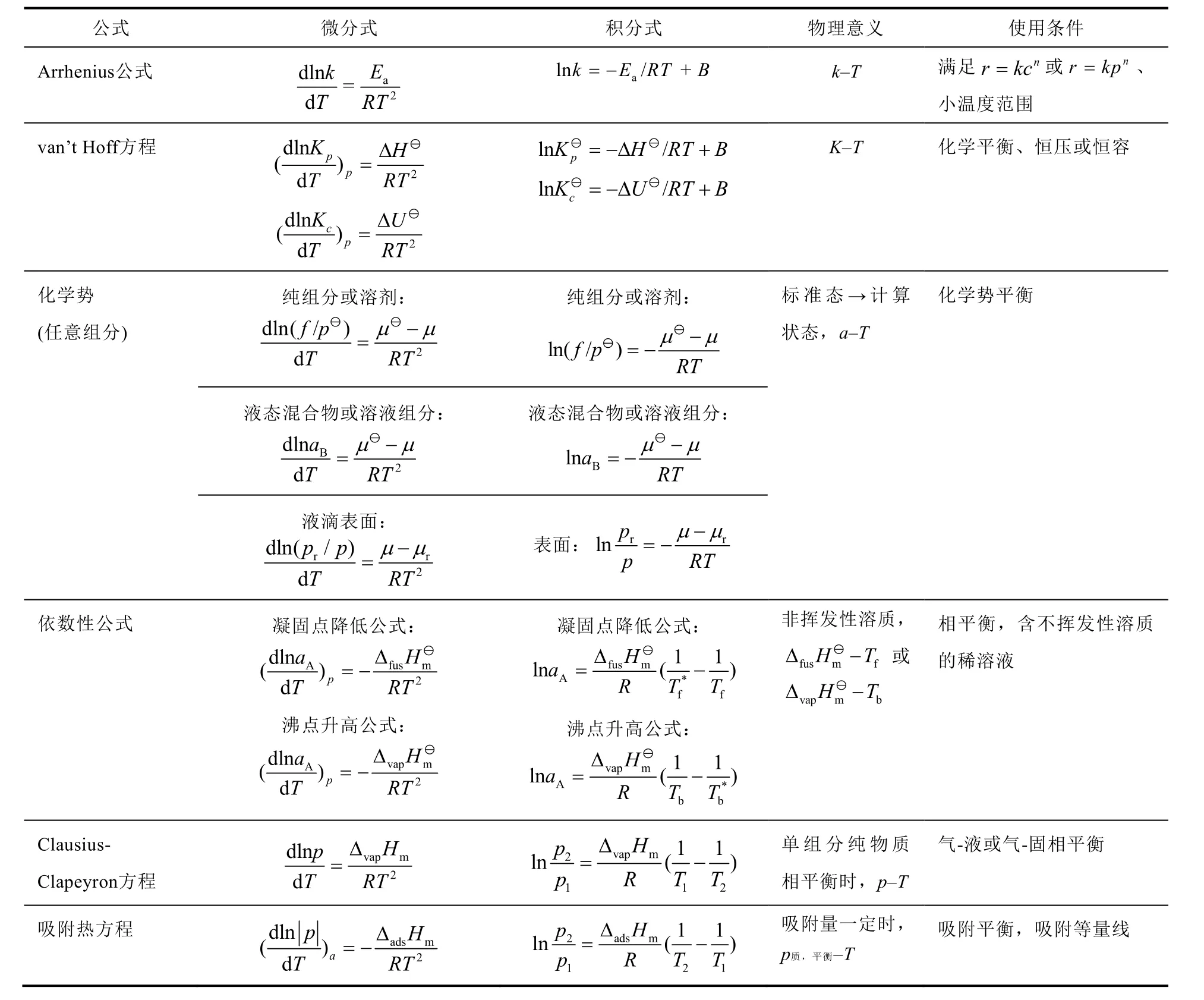
表2 Arrhenius公式及形式相似的熱力學公式匯總

5 結語

從歷史事實看，認為Arrhenius公式是由熱力學的van’t Hoff方程類比而來的說法并不科學。從熱力學出發證明Arrhenius公式無論是從物理意義上還是從哲學角度都不科學。Tolman活化能定義適用于單分子反應，對多分子反應最好引入“分子對”和“活化對”的概念進行修正。首次繪制了Ea-(1/T)-m關系曲面，清晰展示了在較寬的溫度范圍和較廣的m取值下，三常數和二常數Arrhenius公式擬合所得活化能的差異。建議在大學物理化學課程及實驗教學中應廣泛介紹和使用三常數公式Arrhenius公式。明確了物理化學教材中諸多熱力學公式與Arrhenius公式具有相似形式的本質是其所描述的狀態均為達到平衡的對峙過程。