表貼式永磁同步電機模型預測轉矩控制系統預測模型研究*

李耀華, 陳桂鑫, 王孝宇, 劉子焜, 劉東梅, 任 超

(長安大學 汽車學院，西安 710064)

0 引 言

有限狀態集永磁同步電機(PMSM)模型預測轉矩控制(MPTC)充分利用逆變器開關狀態離散有限的特點，將備選電壓矢量遍歷代入磁鏈和轉矩預測模型，得到下一時刻的磁鏈和轉矩，并通過成本函數將磁鏈、轉矩等控制目標柔性統一，靈活實現多目標協同控制，該控制方式受到了高度關注[1-10]。

磁鏈和轉矩預測模型作為MPTC的核心，對系統的控制性能至關重要。根據表貼式永磁同步電機(SPMSM)的磁鏈和轉矩的預測模型建立方法，可分為基于轉子坐標系的MPTC[11-12]、基于定子磁鏈坐標系的MPTC[13-15]和基于靜止坐標系的MPTC[16-17]。不同磁鏈和轉矩預測模型下，SPMSM MPTC系統的性能有所差異。本文建立了基于轉子磁鏈坐標系、定子磁鏈坐標系和靜止坐標系的SPMSM MPTC系統，進行仿真驗證和對比分析，為SPMSM MPTC的選擇提供參考。

1 基于轉子磁鏈坐標系的SPMSM MPTC

轉子磁鏈坐標系下，SPMSMd軸和q軸定子電壓方程如式(1)和式(2)所示:

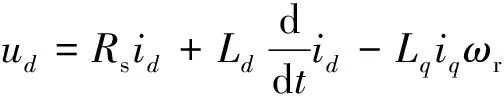
(1)

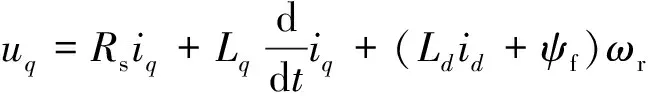
(2)

式中：ud和uq為電機d軸和q軸定子電壓；id和iq為電機d軸和q軸定子電流；Rs為電機定子電阻；ψf為電機永磁體磁鏈；ωr為電機電角速度；Ld和Lq為電機d軸和q軸定子電感。對于SPMSM，d軸和q軸定子電感相等，即定子電感Ls=Ld=Lq。

由于采樣頻率較高，由一階歐拉前向離散公式可得下一時刻的定子d軸和q軸電流的預測值[18]，如式(3)和式(4)所示：

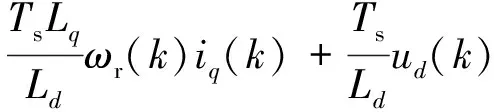
(3)

(4)

式中：Ts為采樣周期。

由下一時刻的定子d軸和q軸電流的預測值，則可得下一時刻的定子磁鏈和轉矩預測值，如式(5)～式(8)所示:

ψd(k+1)=Ldid(k+1)+ψf

(5)

ψq(k+1)=Lqiq(k+1)

(6)

(7)

ψq(k+1)id(k+1)]

(8)

式中：p為極數。

由磁鏈和轉矩預測模型可知，下一時刻的定子磁鏈和轉矩預測值由施加的電壓矢量決定。兩電平三相逆變器產生的備選電壓矢量如式(9)所示[19-20]:

us∈{u0,u1,u2,u3,u4,u5,u6}

(9)

式中：零電壓矢量u0可由兩個開關狀態111或000生成，具體選擇由開關次數最小原則來確定。

由于磁鏈和轉矩量綱不同，需要設計和調整權重系數[21-22]。為了消除權重系數，這里將磁鏈和轉矩均轉換為無量綱的磁鏈和轉矩變化率，設計成本函數[23]如式(10)所示:

g=

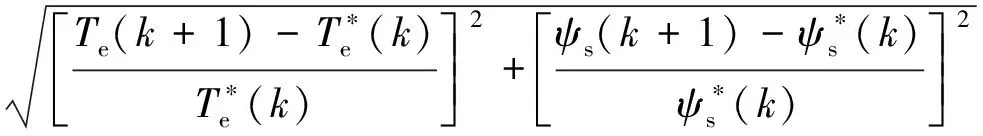
(10)

由此可得，基于轉子磁鏈坐標系的SPMSM MPTC系統如圖1所示。

圖1 基于轉子磁鏈坐標系的SPMSM MPTC系統

基于MATLAB/Simulink建立SPMSM模型預測控制系統仿真模型。仿真模型為離散模型，采樣周期為5×10-5s。直流母線電壓為312 V。轉速PI調節器參數為KP=5，KI=100，輸出上下限為[-30 N·m，30 N·m]。參考轉速初始為500 r/min，2 s時階躍至-500 r/min。負載轉矩初始為10 N·m，1 s時階躍至-10 N·m，3 s時階躍至10 N·m，仿真總時長為4 s。參考定子磁鏈幅值為0.3 Wb。仿真用SPMSM參數如表1所示。

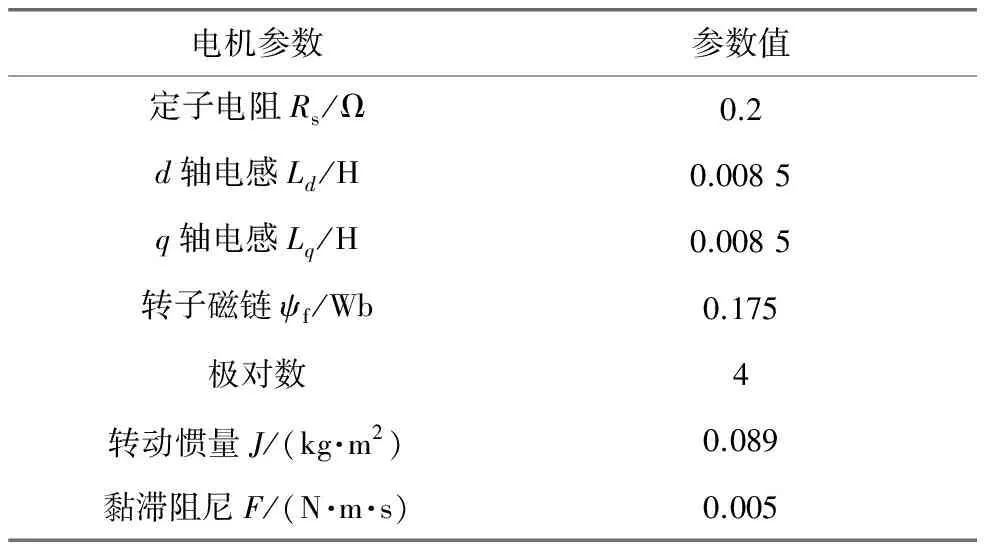
表1 仿真用SPMSM參數

基于轉子磁鏈坐標系的SPMSM MPTC系統仿真結果如圖2～圖4所示。

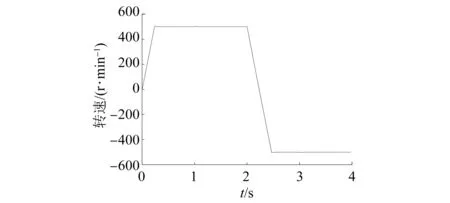
圖2 基于轉子磁鏈坐標系的SPMSM MPTC電機轉速

圖3 基于轉子磁鏈坐標系的SPMSM MPTC電機轉矩

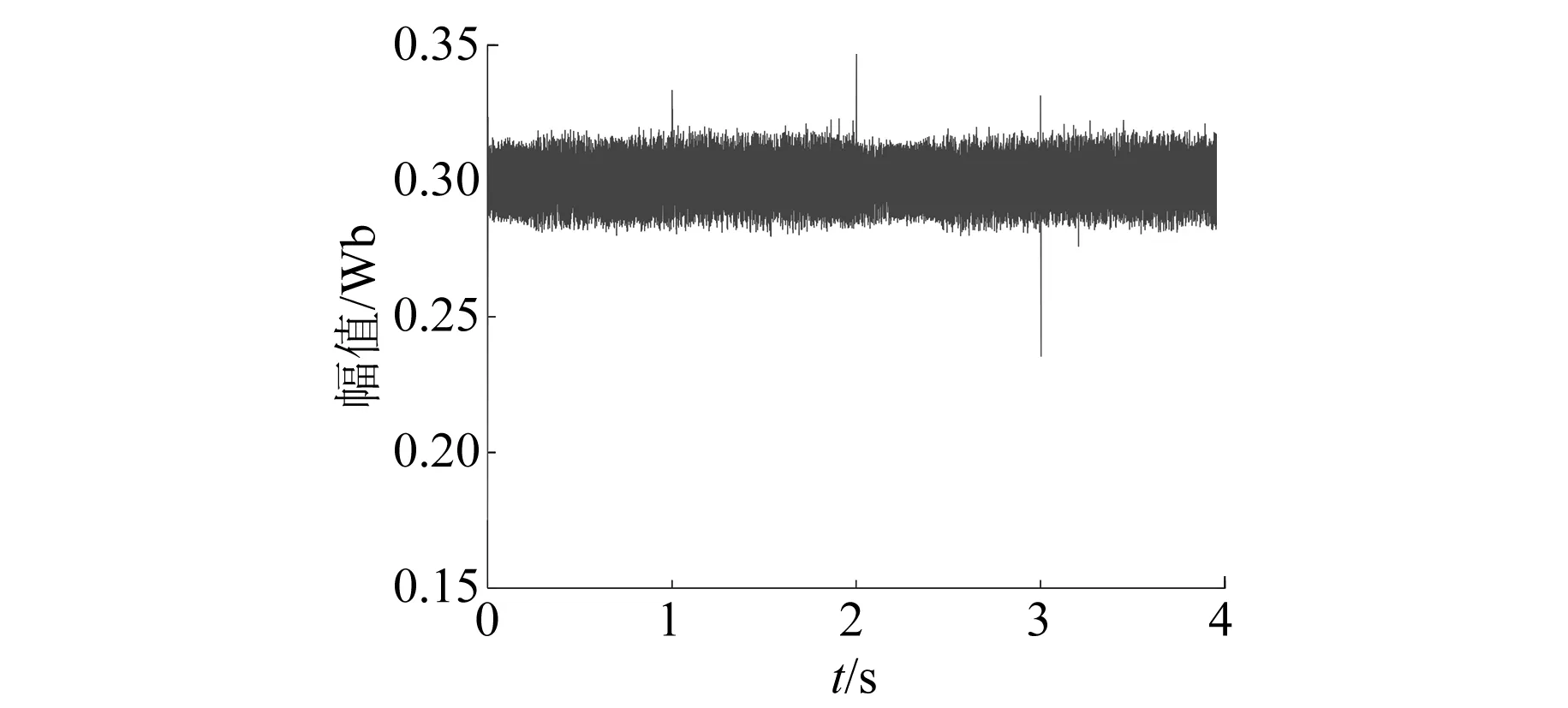
圖4 基于轉子磁鏈坐標系的SPMSM MPTC定子磁鏈幅值

定義轉矩脈動均方根誤差(RMSE)、磁鏈脈動均方根誤差和平均開關頻率fave分別如式(11)～式(13)所示:

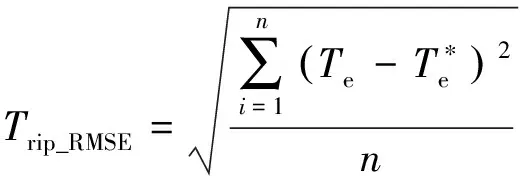
(11)

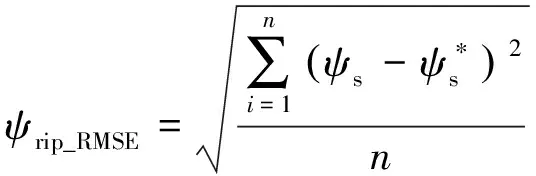
(12)

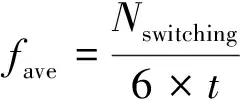
(13)

式中：n為采樣個數;Nswitching為逆變器上下橋臂通斷總次數;t為仿真總時長。

基于轉子磁鏈坐標系的SPMSM MPTC系統控制性能如表2所示。

表2 基于轉子磁鏈坐標系的電機系統控制性能

2 基于定子磁鏈坐標系的SPMSM MPTC

SPMSM定子磁鏈矢量和轉矩如式(14)、式(15)所示:

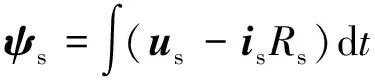
(14)

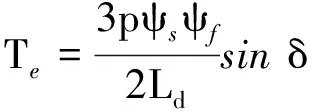
(15)

式中：ψs、us和is分別為定子磁鏈矢量、施加電壓矢量和定子電流矢量;δ為轉矩角，即定子磁鏈與轉子磁鏈夾角。

由式(14)可知，忽略定子電阻壓降，施加電壓矢量一個采樣周期后，定子磁鏈的變化如圖5所示，其中α為施加電壓矢量與定子磁鏈的夾角，Δθs為施加電壓矢量引起的定子磁鏈角度變化。

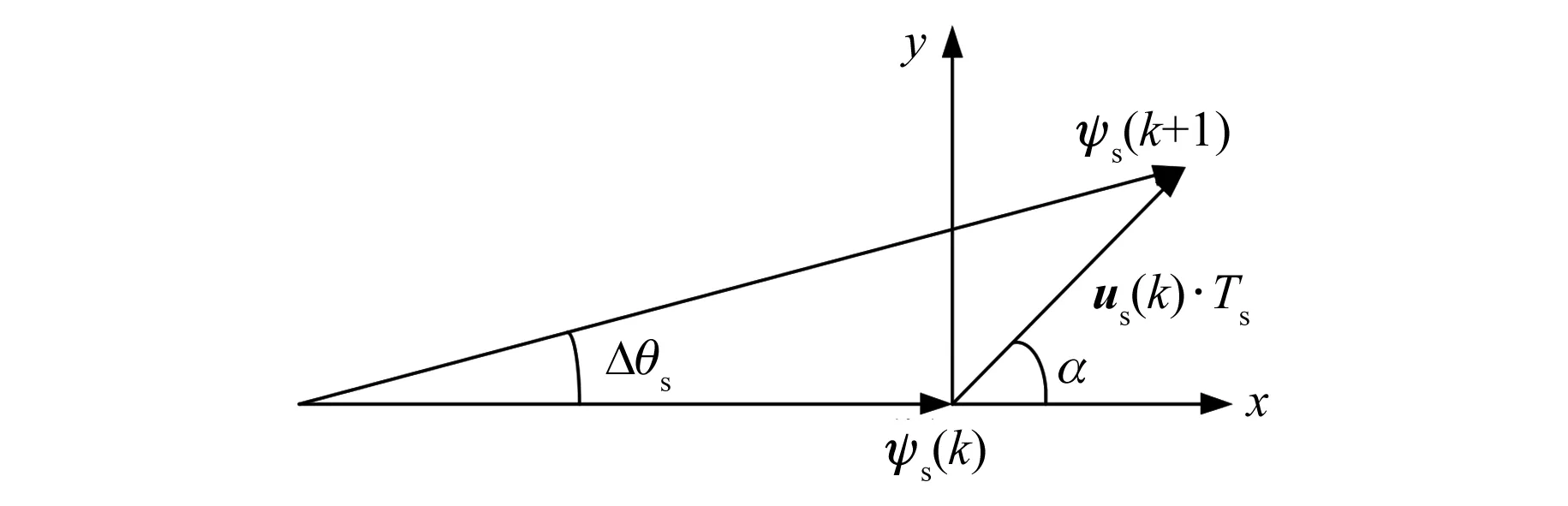
圖5 定子磁鏈變化

由圖5可知，下一時刻定子磁鏈幅值和轉矩角變化量如式(16)和式(17)所示:

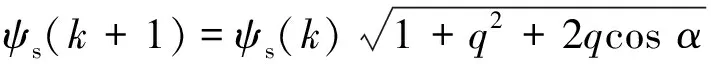
(16)

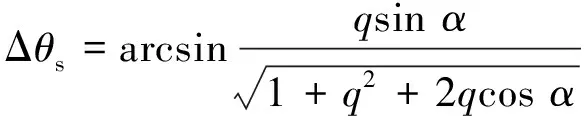
(17)

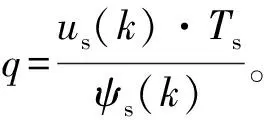
由于采樣周期較小，忽略轉子運動對轉矩角的影響，則下一時刻的轉矩角預測值如式(18)所示:

δ(k+1)≈δ(k)+Δθs=

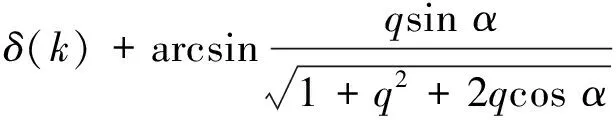
(18)

式中：δ(k)為當前時刻的轉矩角。

由式(18)可知，確定下一時刻轉矩角需確定當前時刻轉矩角信息δ(k)。本文采用反解轉矩方程以獲得轉矩角δ(k)，如式(19)所示:

(19)

將下一時刻定子磁鏈幅值和轉矩角預測值代入至轉矩方程，則可得下一時刻的電機轉矩預測值[24-25]，如式(20)所示:

(20)

由此可得，基于定子磁鏈坐標系的SPMSM MPTC系統如圖6所示。

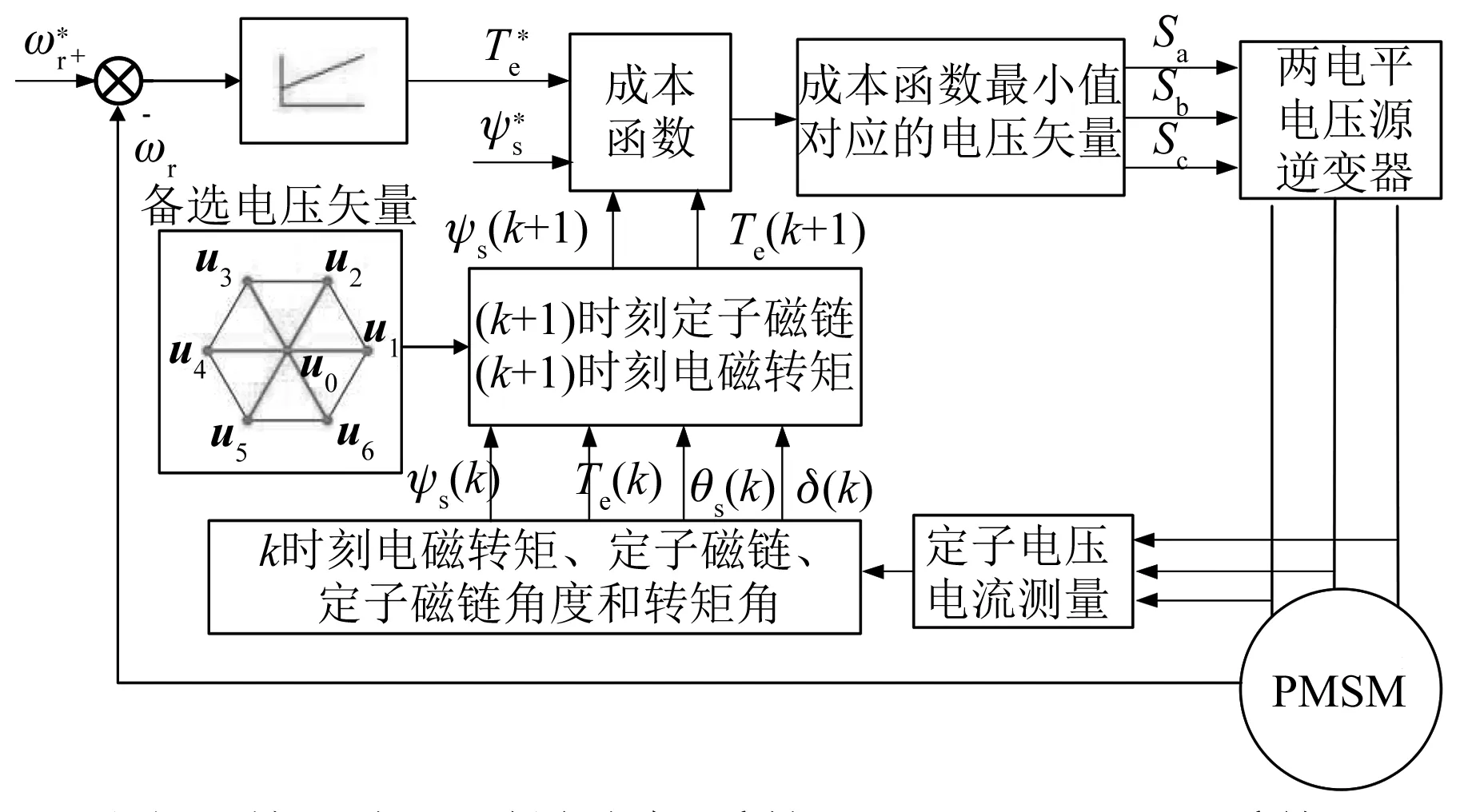
圖6 基于定子磁鏈坐標系的SPMSM MPTC系統

相同備選電壓集合、成本函數及仿真條件下，基于定子磁鏈坐標系的SPMSM MPTC系統仿真結果如圖7～圖9所示。

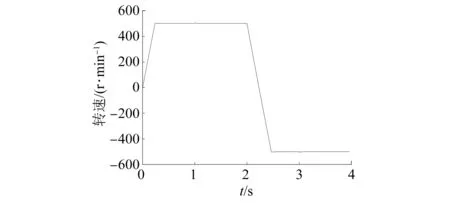
圖7 基于定子磁鏈坐標系的SPMSMMPTC電機轉速

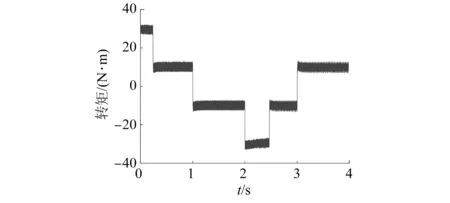
圖8 基于定子磁鏈坐標系的SPMSM MPTC電機轉矩

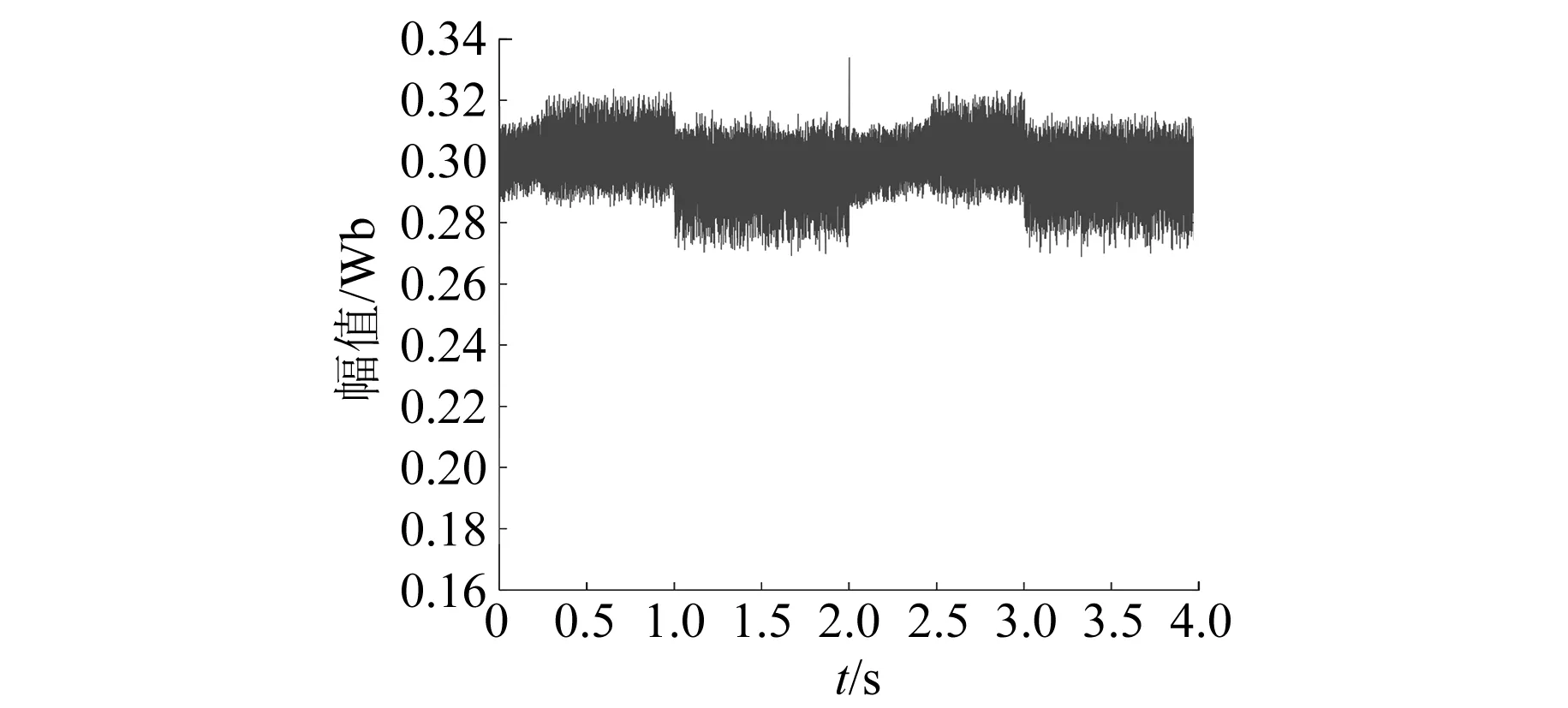
圖9 基于定子磁鏈坐標系的SPMSM MPTC定子磁鏈幅值

基于定子磁鏈坐標系的SPMSM MPTC系統控制性能如表3所示。

表3 基于定子磁鏈坐標系的電機系統控制性能

3 基于靜止坐標系的SPMSM MPTC

SPMSM定子電壓矢量和定子磁鏈矢量方程[26]如式(21)、式(22)所示：

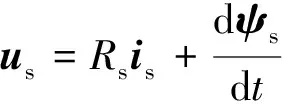
(21)

ψs=Lsis+ψf

(22)

將式(21)代入至式(22)可得：

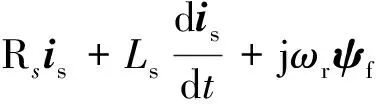
(23)

由于采樣頻率較高，同樣采用一階歐拉前向離散公式將式(23)離散化，可得下一時刻定子電流矢量預測模型如式(24)所示:

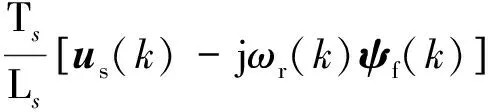
(24)

由上文可知，下一時刻的定子磁鏈矢量預測模型如式(25)所示:

ψs(k+1)=ψs(k)+Tsus(k)-TsRsis(k)

(25)

基于下一時刻定子電流矢量和定子磁鏈矢量預測模型，SPMSM下一時刻轉矩預測模型如式(26)所示:

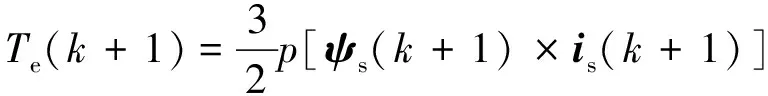
(26)

由此可得，基于靜止坐標系的SPMSM MPTC系統如圖10所示。

圖10 基于靜止坐標系的SPMSM MPTC系統

相同備選電壓集合、成本函數及仿真條件下，基于靜止坐標系的SPMSM MPTC系統仿真結果如圖11～圖13所示。

圖11 基于靜止坐標系的SPMSM MPTC電機轉速

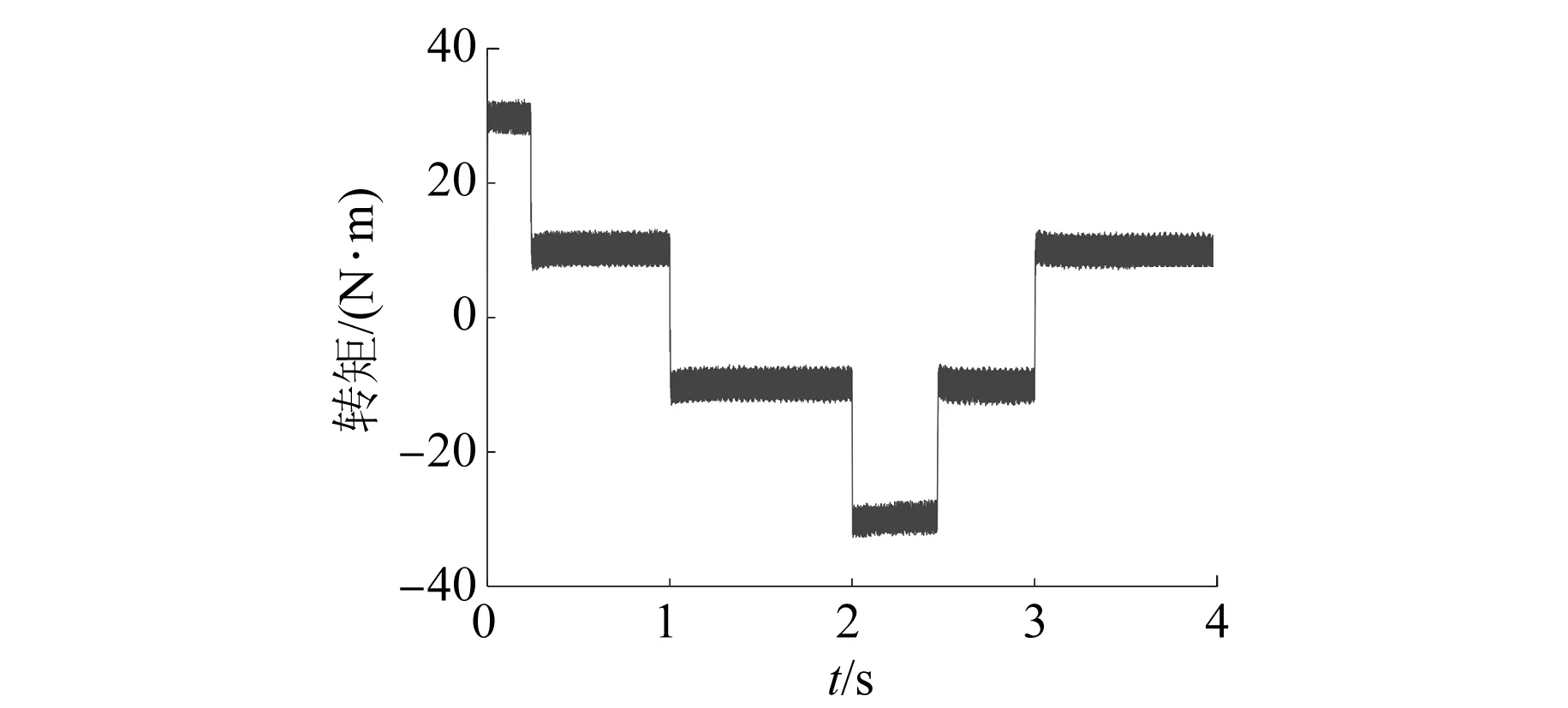
圖12 基于靜止坐標系的SPMSM MPTC電機轉矩

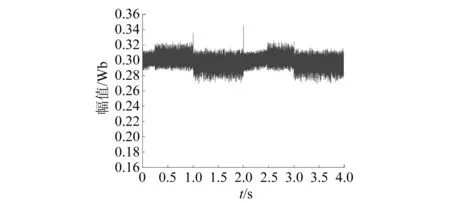
圖13 基于靜止坐標系的SPMSM MPTC定子磁鏈幅值

基于靜止坐標系的SPMSM MPTC系統控制性能如表4所示。

表4 基于靜止坐標系的電機系統控制性能

4 結 語

(1) 基于轉子磁鏈坐標系、基于定子磁鏈坐標系和基于靜止坐標系的SPMSM MPTC可行，電機系統可實現四象限運行。

(2) 不同磁鏈和轉矩預測模型對磁鏈和轉矩的計算有所差異，導致SPMSM MPTC系統控制性能不同。基于轉子磁鏈坐標系的SPMSM MPTC性能較優，但平均開關頻率較高。基于定子磁鏈坐標系和靜止坐標系的SPMSM MPTC性能基本相當，轉矩脈動較大，但平均開關頻率較低。

(3) 基于轉子磁鏈坐標系的SPMSM MPTC需要轉子實時位置和旋轉坐標變換以獲得電機定子d、q軸電流分量。基于定子磁鏈坐標系和基于靜止坐標系的SPMSM MPTC可不依賴轉子位置實現，從而減小對轉子實時位置信息的依賴。