不同加載方式對輸電鐵塔風致響應的影響

伍川， 張博， 劉澤輝， 楊曉輝， 李超， 趙洋*

(1.國網河南省電力公司電力科學研究院， 國網輸電線路舞動防治技術重點實驗室， 鄭州 450052； 2.重慶郵電大學先進制造工程學院， 重慶 400065)

輸電塔線體系承擔著電能的傳輸、分配、調節(jié)等作用，其安全性和穩(wěn)定性非常重要，因惡劣氣候條件而引起的架空輸電線路破壞會導致電力系統(tǒng)癱瘓，帶來的后果不可估量[1]。風載荷作為最常見的外部載荷，在高壓輸電線路桿塔設計中需要特別關注。

輸電塔線體系由于其復雜的耦合效應特性會使其風振響應的評估過程變得十分復雜[2]，學者們主要從靜力分析和動力響應分別探討其力學性能。厲天威[3]建立臺風工況下“三塔兩檔線”的塔線耦聯(lián)體有限元模型并對其進行靜力學計算，表明塔線耦聯(lián)作用不可忽略。雒億平等[4]分析靜力風載作用下的羊角形輸電塔的軸力，發(fā)現輸電塔主材承受的軸力大于輔材承受的軸力。丁志敏等[5]建立了“四塔五檔線”模型，研究了塔線耦合體系的固有模態(tài)及振型，驗證了導地線剛度小于鐵塔構件剛度。盧銀均等[6]建立了“兩塔三檔線”有限元模型，分析了塔線體系前300階自振頻率和振型，結果表明塔線體系在低階模態(tài)時，導地線振動頻率低于鐵塔頻率，在高頻振動下主要以鐵塔振動為主。于志強[7]建立了“兩塔三檔線”塔線體系的有限元模型，分析了其風振反應，認為輸電線的存在增大了塔線體系的自振周期。謝文平等[8]建立了輸電塔線體系的有限元模型，分析了塔線體系在強風作用下的風振響應，研究表明，隨著高度的增加，輸電塔峰值位移響應迅速增加，且橫向振動明顯大于縱向振動。Qin等[9]建立了雙回路直線轉角塔的有限元模型，對輸電塔線系統(tǒng)的時域分析進行了研究，得到脈動風荷載對輸電塔線系統(tǒng)的影響大于靜風荷載對輸電塔線系統(tǒng)的影響。Zhang等[10]建立了輸電塔線耦合系統(tǒng)的有限元模型，分析了塔線系統(tǒng)的動力響應，結果表明，風速增大會使耦合效應逐漸變得顯著，可能導致塔線系統(tǒng)有過早失效的風險。王彥海等[11]建立“兩塔三檔線”的有限元模型，分別對塔線體系在無風工況下的抗變形能力和設計風速工況下的動力響應進行分析，結果表明，風載荷會使輸電塔線體系承受塔腿變形的能力明顯降低。同時研究人員還進行了風致響應的靜、動力學對比分析。裴慧坤等[12]建立了“三塔兩檔線”模型，對其進行動、靜力學分析，認為動力響應情況下的應力、位移時程曲線指標均大于靜力風荷載下的相應指標。唐磊等[13]建立了“三塔兩檔線”模型，計算了輸電塔在隨機風場中的動力響應及等效靜力響應，動力學計算得到的主材、斜材應力均大于等效靜力計算得到的結果。He等[14]建立了“三塔兩檔線”的有限元模型，對比進行了準靜態(tài)分析和動力學分析，同樣表明動態(tài)響應大于靜態(tài)響應。雖然目前對輸電線路風載作用下的力學性能研究已經有了一些進展，但對桿塔風致響應不同建模及加載方式的認識還不夠全面。

為了系統(tǒng)研究輸電鐵塔風致響應中不同加載方式及耦合形式對桿塔的影響，現以500 kV輸電線路中一酒杯型輸電鐵塔為中心的“一塔兩檔線”為研究對象，分別建立隨機風載塔線分離、隨機風載塔線耦合及等效靜力風載三種有限元模型研究輸電鐵塔的力學性能，分析其位移與應力響應。分析結果可為研究輸電塔線體系在風載荷作用下的力學性能以及后續(xù)諸如桿塔上的螺栓松動等不同問題時的模型選擇提供參考。

1 塔線體系幾何模型

1.1 塔線模型

研究對象為500 kV線路一典型耐張段，中間為酒杯型直線塔，塔高48.2 m，呼稱高度為42 m，選取與兩側耐張塔的檔距均為400 m。輸電鐵塔塔身主斜材為Q420、Q345鋼，其余輔材為Q235鋼，根據其桿件承載特點，采用空間桿梁混合單元建立其有限元幾何模型。

輸電導地線是一種柔性結構，只承受拉力，其剛度小、跨度大、非線性程度高。可以利用ABAQUS中不考慮壓縮彈性模量的三維桿單元來模擬導線的索單元屬性。該線路導地線參數如表1所示。

表1 導地線材料屬性Table 1 Material properties of lines

1.2 金具模型

在研究輸電鐵塔風致響應時，線路上金具的細節(jié)對桿塔結果的影響可以忽略，在保證其等效質量和特征尺寸的前提下，可以簡化其外部形狀。I型、V型絕緣子串以及耐張絕緣子串模型均用圓截面梁模擬，截面半徑為0.01 m，然后進行質量的等效。間隔棒采用邊長為0.45 m的正方形模擬，相鄰間隔棒之間的距離為20 m。

根據以上的建模方法，依次建立輸電鐵塔模型、導地線模型、絕緣子模型，組成“一塔兩檔線”的輸電塔線體系模型，如圖1所示。

圖1 輸電塔線體系模型Fig.1 Transmission tower-line system model

2 風載荷的計算

2.1 輸電鐵塔風載荷

輸電塔不同高度處的風速不同，將鐵塔的風載荷分8段計算，為了保證足夠的安全裕度，取每個部分的最高點作為典型點，將典型點的風速用于整段部分的風載荷計算。具體分段情況如圖2所示。

在B類地貌中，高度h處的風速Vh計算公式為

(1)

式(1)中：V10為離地10 m高的設計基準風速。

作用在與風向相垂直的輸電塔的基本風壓W0計算公式為

(2)

計算得到輸電鐵塔在不同高度位置的基本風壓如表2所示。

圖2 輸電鐵塔分段示意圖Fig.2 Schematic diagram about each part of transmission tower

2.2 導地線風載荷

導地線在初始應力和重力影響下存在一定的弧垂，根據找形理論，導地線的空間位形為懸鏈線，經計算可得該檔距下導地線的弧垂分別為11.58 m和8.05 m。

表2 輸電鐵塔不同位置處的風速與風壓Table 2 Wind speed and pressure at different positions of transmission towers

考慮到導地線各點高度的差異對風速的影響較大，將檔距400 m劃分為50段，沿線路水平方向每隔8 m模擬一個風速樣本，風模擬點的坐標選取每段導線的中點坐標。在模擬風速時，采用工程中廣泛使用的Kaimal風速譜，模擬脈動風速時程樣本。該輸電線路所處地型為B類地貌，地面粗糙系數α取0.16，地面粗糙長度取0.03，模擬的總時長為120 s，時間步長為0.5 s，頻率的截取范圍為0.0～6.28 rad/s，頻率范圍等分數為3 000。模擬風場的設計基準風速為30 m/s。

圖1中所示的第1、15、25三個模擬點的風速時程曲線如圖3所示，將模擬得到的風速曲線進行譜分析得到功率譜S(ω)(ω為圓頻率)，其與Kaimal譜對比結果如圖4所示，可見模擬脈動風的風速功率譜與Kaimal譜吻合。

基本風速為30 m/s時點25風速的自相關函數R25，25以及點25與點1和點15的互相關函數R25，15、R25，1如圖5所示，可以看出，距離越遠，兩點的相關性越低，與實際情況相符合。根據上述的分析，能夠證明模擬風速時程樣本的合理性。

根據中國電力行業(yè)標準，計算電線風載荷的表達式為

(3)

式(3)中：Wx為垂直于導線軸線的水平風載荷；α為風壓不均勻系數；βc為500 kV線路風載荷調整系數；μsc為導線或地線的體型系數；d為導線或地線的外徑；lH為桿塔之間的水平檔距；θ為風向與導線或地線方向之間的夾角；μz為風壓高度系數。

根據上述模擬的脈動風速及風載荷計算公式，便可計算得到對應導線、地線上的隨機風載荷。

3 不同加載及耦合方式下的輸電鐵塔性能分析

3.1 塔線分離模型動力響應

塔線分離模型的建模過程：首先建立單獨的兩檔400 m導線有限元模型，將兩檔線用懸垂絕緣子連接，并限制懸垂絕緣子串上端點的平動自由度；導線兩端各連接一個耐張絕緣子串，耐張絕緣子串外側端點只具有繞導線方向的旋轉自由度；最后對導線施加2.2節(jié)中模擬得到的脈動風載荷，進行動力學分析得到懸垂絕緣子串上端點的支反力時程曲線，地線支反力的提取與導線類似。

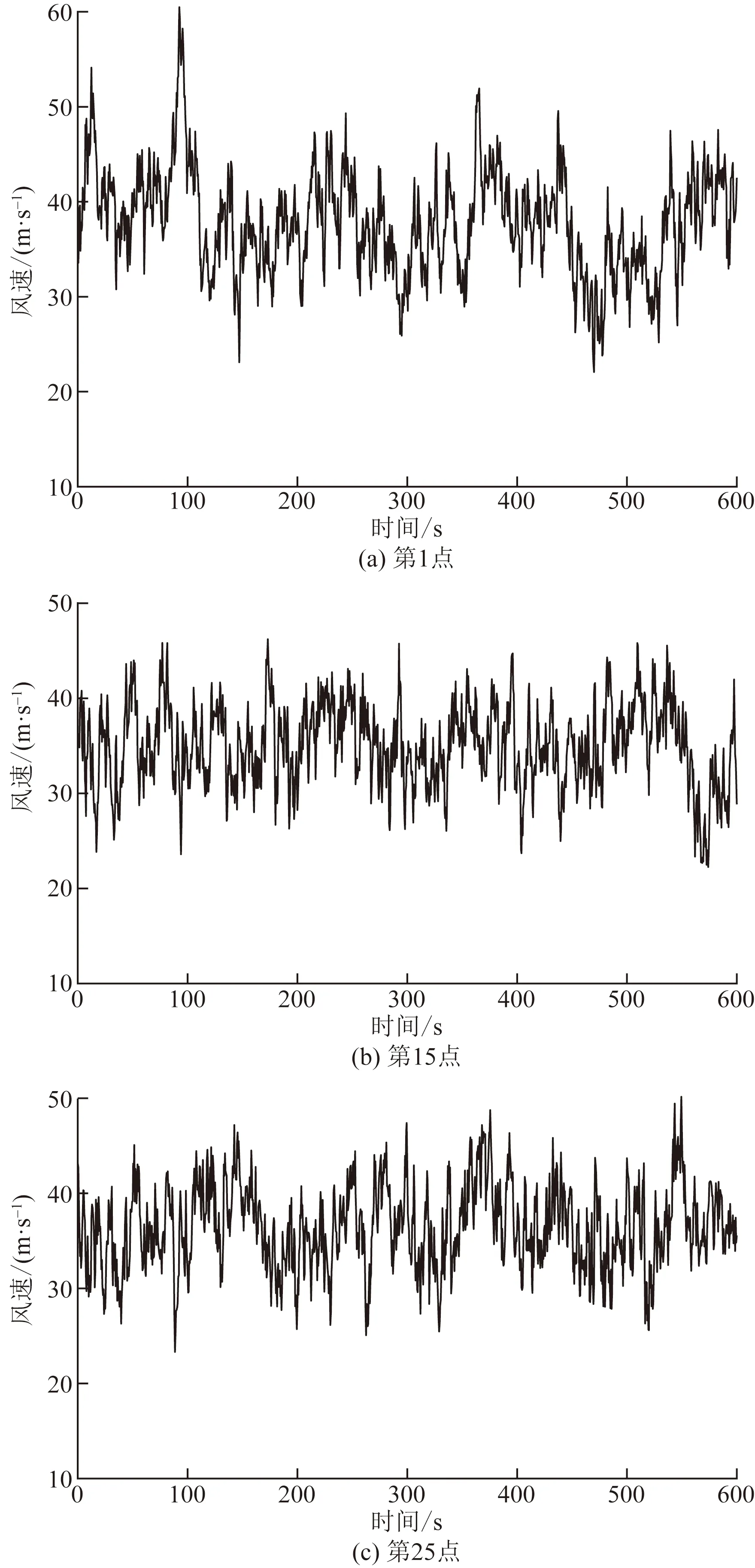
圖3 模擬點的風速時程曲線Fig.3 Wind speed time history curve at simulated points

圖4 模擬脈動風速功率譜與Kaimal譜的對比Fig.4 Comparison between simulated fluctuating wind speed power spectrum and Kaimal spectrum

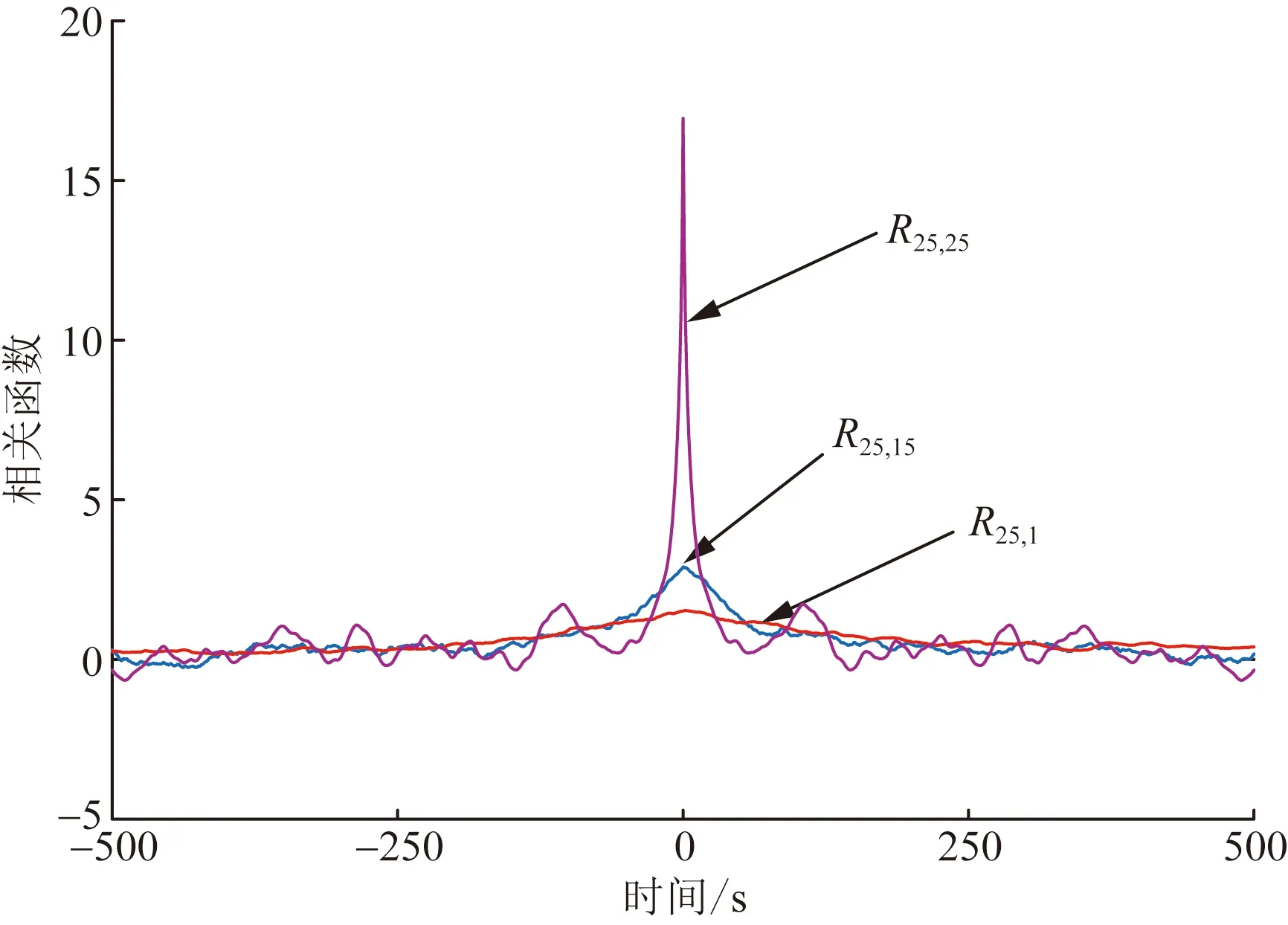
圖5 第25點模擬風速的自相關函數及與 代表點風速的互相關函數Fig.5 Autocorrelation function of point 25 simulated wind speed and the cross-correlation function with the wind speed of representative points

將導地線絕緣子串各端點提取的支反力以相互作用力的形式施加到掛點上，可以模擬導地線對輸電鐵塔所帶來的影響。同時根據表2中的風壓數據，對輸電鐵塔各部分施加相應的風載，并對塔腳施加固定約束，然后進行動力學分析。輸電鐵塔桿件在迎風面受到拉力作用，背風面受到壓力作用。如圖6所示為t=12.82 s時刻的鐵塔應力和位移分布情況，可見該時刻除了塔腳應力集中外，應力最大值出現在塔身第二部分的主材上，為209.19 MPa，這與大多數受風倒塌的鐵塔破壞位置是吻合的，在設計過程中應引起特別關注。位移作為最直觀的輸出，是判斷鐵塔變形程度的重要依據，由圖6(b)可知，最大位移出現在塔頭處，為280.77 mm。

3.2 塔線耦合模型動力響應

塔線耦合模型是將輸電鐵塔和導地線耦合為一個系統(tǒng)，同時對導地線和塔身施加相應的風載荷。塔線耦合模型的塔腳以及耐張絕緣子串處的邊界條件與塔線分離模型完全一致。不同之處體現在懸垂絕緣子串通過“Join + Rotation”連接器與掛點相連，不再單獨設置其邊界條件[15]。同樣對該系統(tǒng)進行120 s動力學計算，t=12.33 s時刻的塔線耦合系統(tǒng)受風載荷作用下的變形示意圖如圖7所示。對比塔線分離模型，應力危險區(qū)域位于同一位置，應力最大值為211.13 MPa，位移最大值位置依然位于塔頭處，值為284.01 mm。

圖6 塔線分離模型鐵塔應力與位移值分布Fig.6 Stress and displacement distribution diagram of tower-line separation model

3.3 等效靜力風載荷響應研究

無論塔線分離還是塔線耦合模型的計算都會消耗大量的建模以及計算時間，尤其是在計算多種風速、風向角等不同影響因素的情形下。為了提高效率，采用等效靜力加載的方式研究輸電鐵塔的風致響應。

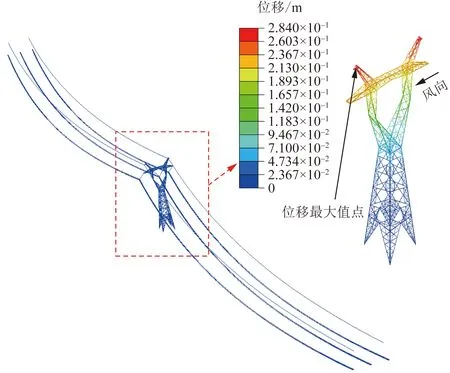
圖7 風載荷作用下的塔線耦合模型變形示意圖Fig.7 Deformation diagram of tower-line coupling system under wind load

將導線和地線所受的風載荷等效為靜力作用，相應的靜力風載荷計算公式為

Wx=αμscβcdlHW0sin2θ

(4)

式(4)中：W0為基本風壓。根據計算，可得在30 m/s設計基準風速、90°風向角工況下的四分裂導線上的等效靜力風載荷為33.32 kN，地線上的等效靜力風載荷為4.90 kN。

輸電鐵塔的邊界條件與塔線分離模型一致，只有塔腳位置設為固定約束，忽略塔線之間振動的相互影響，將等效靜力風載荷直接施加到掛點上，塔身仍然考慮風載荷作用，然后對其進行靜力學分析。應力危險區(qū)域仍然出現在輸電鐵塔的第2部分的相同位置，應力值為183.97 MPa，最大位移值的位置出現在塔頭處，位移值為261.74 mm。

3.4 不同加載及耦合方式下結果對比

分別提取塔線分離、塔線耦合及等效靜力模型響應結果，其中塔線分離及耦合模型的塔身危險位置的應力與位移時程曲線如圖8所示。

由圖8可知，塔線耦合與分離情況下的應力與位移響應的變化趨勢基本一致，對應的數值相差很小。但是由于塔線耦合效應的存在，使得輸電鐵塔的應力分布以及位移響應頻繁波動，桿件所承受的交變載荷會對其安全性能產生影響。

三種不同計算模型的應力危險區(qū)域均相同。塔線分離和耦合模型采用的動力學計算方法，其危險區(qū)域的應力和位移最大值以及穩(wěn)定后的平均值、等效靜載模型相同位置的力學性能如表3所示。

圖8 塔身危險位置的應力與位移時程曲線Fig.8 Time history curves of stress and displacement at the dangerous position of the tower

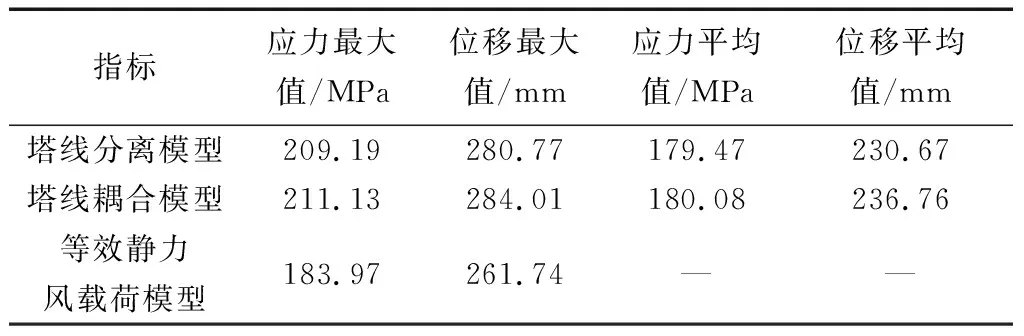
表3 三種模型結果對比Table 3 Comparison between three models

可見，風載荷導致的桿塔力學性能動力學計算指標均大于靜力學效應的相應指標。在研究輸電鐵塔桿件屈服等問題時，等效靜力風載荷的應力響應不能作為判斷依據。同時注意到等效靜載模型的最大位移值是小于動力學計算結果的，這是由于等效靜力時并未考慮導地線重力和塔線耦合的影響。但是等效靜力風載荷模型計算得到的應力值非常接近動力學計算的平均值，可以作為快速近似估計其動力風載荷平均應力響應的一種途徑。相較于其他兩種模型，等效靜載模型計算效率高，可用于后續(xù)計算構件的軸力變化進而評估螺栓連接松動特性研究。

4 結論

建立了500 kV線路耐張段“一塔兩檔線”分離、耦合動力學模型以及等效靜力學模型。分別計算輸電鐵塔和導地線的隨機風載及等效靜載，并施加到相應的模型上，對其應力和位移響應進行對比分析。

(1)三種計算模型均顯示危險區(qū)域位于塔身主材上，通過對比塔線分離模型和塔線耦合模型的桿塔力學性能可知，由于塔線耦合效應的存在，使得輸電鐵塔的應力分布以及位移響應頻繁波動，其承受的交變載荷會對其安全性能產生影響。

(2)塔線系統(tǒng)動力學模型得到桿塔上的應力和位移最大值均大于等效靜力風載荷模型，動力學分析在評估桿塔性能時不可忽略。

(3)等效靜載模型計算效率高于其他兩種模型，可用于快速近似估計其動力風載荷平均應力響應，也可用于后期桿件的軸力計算，快速評估螺栓的橫向載荷。