圓柱度誤差下長徑比對滑動軸承運行特性的影響

魏晉鵬，徐武彬，李 冰，張子文

（廣西科技大學機械工程學院，廣西 柳州 545006）

1 引言

由于滑動軸承具有較高的承載能力，高旋轉精度被廣泛應用于大型旋轉機械中，作為回轉部分的主要部件，研究其運行特性非常重要。文獻［1］通過研究在不同長徑比下的轉子系統定點碰撞的力學特性，發現系統的運動狀態會隨著長徑比的變化而產生改變。當長徑比在（0，1］內波動時，各種動力學特性會存在于轉子系統中。轉子系統風車碰摩安全裕度隨著擠壓油膜阻尼器長徑比的增大呈現先增大后緩慢較小的趨勢。文獻［2］研究了長徑比對Savonius 轉子性能的影響。研究發現，長徑比增大的同時，最大功率系數的功率系數和葉尖速度比也會增加。對于較低的長徑比，風位移超過轉子的影響更為強烈。文獻［3］通過fluent仿真分析油膜的變化規律，計算結果表明隨著轉速，長徑比的增大，軸承的最大壓力，承載力最高溫度等也會增大。文獻［4］提出一種新的計算方法，在這個基礎上他研究了長徑比，偏心率等對于油膜空穴和壓力分布的影響，研究結果表明油膜壓力隨長徑比的增大而增大。文獻［5］基于雷諾方程對各結構參數下的油膜壓力和承載力進行了分析，研究結果表明較大的長徑比和偏心率會產生較大的油膜壓力和承載力，但承載力作用角的變化與長徑比無關。文獻［6］也是通過fluent 進行油膜仿真得到如下結果，其他條件一定，長徑比越大油膜壓力的最大值也就越大，軸承的承載能力也就越強，且最大壓力的位置與轉速無關。文獻［7］針對單跨雙盤轉子系統建立了集中質量模型，分析了長徑比，軸承間隙等參數對系統振幅的影響，研究結果表明各參數在低速下振幅變化程度一致，在高速旋轉時振幅變化存在差異。文獻［8］用分離變量法構建模型，研究了長徑比，偏心率等對非線性油膜力的影響，研究結果表明長徑比在（0.25～0.8）時油膜壓力與油膜力成拋物線和近似指數分布，且長徑比等于0.8時在一定油膜域有好的一致性。通過上述文獻可以看到研究長徑比對滑動軸承的影響很有意義。這里建立了存在圓柱度誤差的系統動力學模型，研究圓柱度誤差下不同長徑比對滑動軸承運行特性的影響。

2 滑動軸承油膜力模型及計算方法

2.1 計入圓柱度誤差下滑動軸承系統動力學模型

圓柱度誤差是指實際圓柱面要素對其理想圓柱面的變動量［9］。在圓柱度誤差定義中存在兩種典型圓柱度就是馬鞍形與鼓形。鼓形對軸承轉子系統的承載力、穩定性、能量損失都是有利的，而馬鞍形則剛好相反。在誤差等級方面，當圓柱度的誤差等級小于9等級時，它對軸承轉子系統的承載力、穩定性、能量損失的影響幾乎保持不變。在此理論基礎上這里選擇的轉子系統存在圓柱度（鼓形）誤差，且誤差等級為12等級，考慮不同長徑比對存在圓柱度時的工作運行特性是否有影響。

建立滑動軸承油膜力學模型，并且將軸頸圓柱度誤差（鼓形）考慮其中，如圖1所示。其中，Z軸為中心軸線，rb為軸瓦半徑，Oj為軸頸中心，Ob為軸瓦中心，rj為軸頸半徑，L為軸承長度，Y軸在軸瓦長度的L∕2截面處。滑動系統的初始偏心距為|ObOj|=e，圖中θ和Φ分別為轉子系統處于穩定工作狀態時的位置角和姿態角，h為軸頸和軸瓦間的實際油膜厚度。隨著軸頸形狀誤差的變化，軸頸半徑rj也會變化，同時也使得軸頸與軸瓦之間的距離c發生改變，其中c=rb-rj。

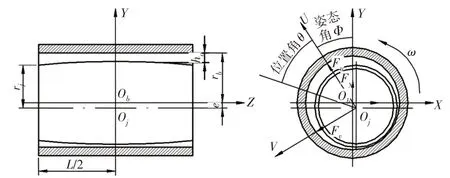
圖1 計入轉子圓柱度誤差下滑動軸承系統動力學模型Fig.1 Dynamic Model of Sliding Bearing System Considering Rotor Shape Error

普通滑動軸承的油膜厚度為：

為了計算帶有圓柱度誤差的滑動軸承任意截面處油膜厚度h，需要計算軸向半徑偏差Δr，Δr隨Z軸和角度發生變化，Δr關于Z和θ的函數如下：

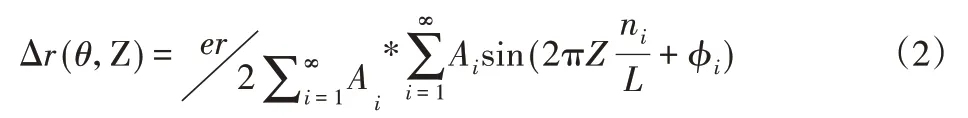
式中：Ai—圓柱度誤差系數；

er—圓柱度誤差等級；

L—軸承長度；

φi—圓柱度的初始相位角，ni=1，2，3，…。

因此，由式（1）、式（2）可得帶圓柱度的滑動軸承轉子系統任意位置的油膜厚度，表示如下：

式中：ε—偏心率，ε=e∕c。

如圖1所示，油膜力與自身的運動狀態和位置有關。這里通過有限差分法求解Reynolds方程來確定油膜壓力，進而確定軸頸上的油膜力分量［10］，即FU和FV。

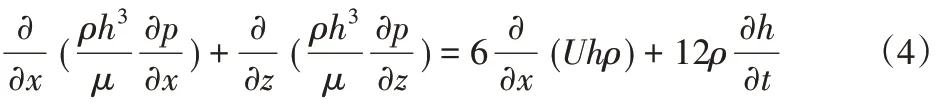
式中：P—油膜壓力；

h—油膜厚度；

ρ—油膜密度；

U—軸頸表面速度（包括徑向速度和切向速度）；

t—時間；

x，z—圓周方向和徑方向坐標。

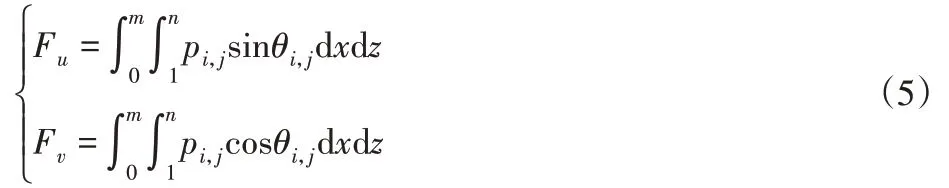
式中：FU和FV—U和V方向上的油膜力；p—油膜壓力；θ—位置角。

圖1中Fx，Fy—FU和FV在水平方向和豎直方向的分力。

2.2 轉子系統承載特性

這里描述的是轉子系統，當系統處于穩定狀態時，油膜壓力在水平方向上的分量Fx=0。用其豎直方向上的油膜力Fy表征滑動軸承系統的承載力。為了表征圓柱度誤差對轉子系統承載能力的影響，這里通過無量綱參數Sommerfeld建立了轉子系統動態特性和系統結構參數的關系。Sommerfeld數與承載力成反比，即Sommerfeld越小承載能力越強。

該計算公式為［11］：

式中：μ—流體的動力學粘度（Pa·s）；

N—轉速（r∕min）；

L—滑動軸承的長度（m）；

rj、Db、c—軸頸半徑（m）、軸瓦直徑（m）及軸承間隙（m）；

Fy—軸承的載荷（N）。

2.3 轉子系統穩定特性

這里引入了無量綱運行參數Op，此參數用來對系統運行穩定性進行量化評估。在此之前需要通過軸心軌跡圖形的來判斷臨界轉速［12］，通過計算無量綱參數Op來表示滑動軸承系統的工作狀態。

運行參數OP的公式為［13］：

式中：F—軸承所承受的載荷（即軸承重力mg）；

m—軸承系統質量；

ω—系統的穩定性臨界轉速。

2.4 滑動軸承摩擦功率損耗

滑動軸承運行穩定時，軸頸在轉動過程中會有來自潤滑油和軸瓦間的摩擦阻力，會給運行中的系統帶來損耗。它在轉子系統的能量損失中占了很大比例，所以降低摩擦損耗是提高轉子系統工作效率的必要環節，也是軸承系統設計工作的必要環節。轉子系統摩擦功率損耗的計算公式如下［14］。

式中：μ—潤滑油粘度；

L—軸承長度；

vτ—轉子系統穩定狀態下軸頸切向速度；

c—半徑間隙；

ε—偏心率。

3 圓柱度誤差下不同長徑比對滑動軸承運行特性的影響

3.1 圓柱度誤差下長徑比對滑動軸承承載能力的影響

依次為長徑比（L∕D）等于0.5、0.8、1、1.2 下的滑動軸承系統結構參數，如表1 所示。0 等級為不存在圓柱度誤差（普通滑動軸承）的滑動軸承，12 等級為存在圓柱度誤差的滑動軸承。0等級與12 等級下不同長徑比時滑動軸承Sommerfeld 數在不同偏心率時的變化情況，如圖2 所示。從圖2 可以明顯的看到隨著轉子長徑比的不斷增加，Sommerfeld 數曲線不斷地向左偏移，即0 等級與12 等級下Sommerfeld 數都隨著長徑比的增加而減小，Sommerfeld 數的減小說明軸承系統的承載能力在提高。此結果表明圓柱度誤差存在與否不影響長徑比對軸承承載能力的影響，即無論是否存在圓柱度誤差長徑比的增加都有利于承載力的提高。

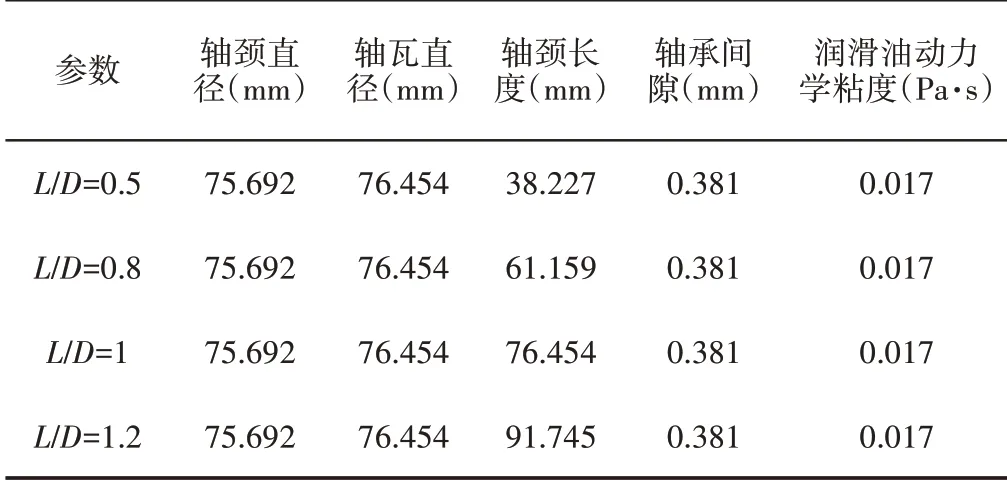
表1 滑動軸承系統參數表Tab.1 The Parameters of Hydrodynamic Journal Bearing System

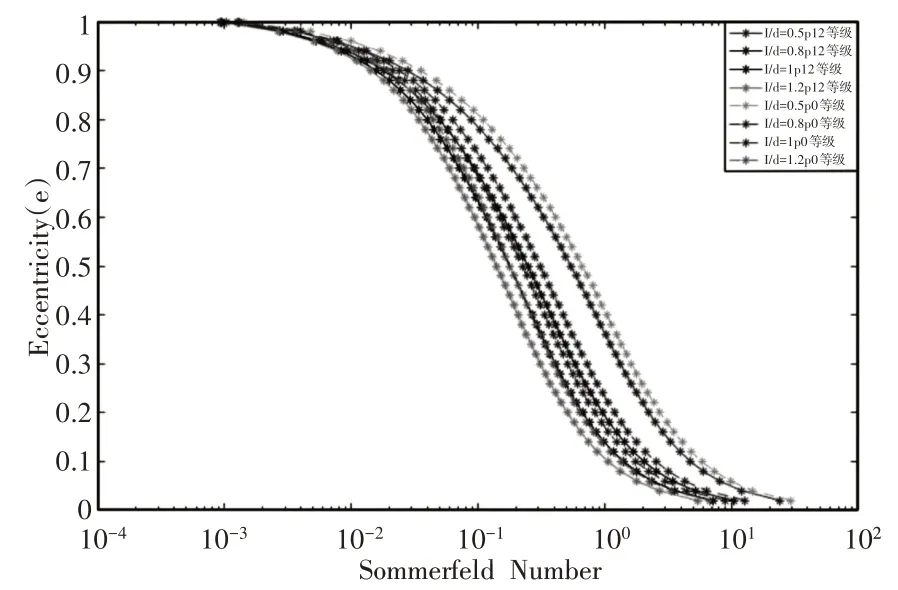
圖2 不同長徑比下Sommerfeld數與偏心率的關系Fig.2 Relationship between Sommerfeld Number and Eccentricity under Different Aspect Ratios

3.2 圓柱度誤差下長徑比對滑動軸承運行穩定性的影響

為了研究存在圓柱度誤差時不同長徑比對軸承系統穩定性的影響，引入無量綱參數Op，滑動軸承0 等級與12 等級時不同長徑比下無量綱參數Op隨偏心率變化的穩定性曲線，如圖3所示。

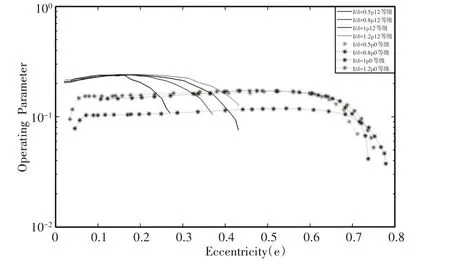
圖3 不同長徑比下Op數與偏心率的關系Fig.3 Relationship between Opnumber and Eccentricity under Different Aspect Ratios

觀察圖3可以得到，12等級當偏心率ε≤0.15時，Op曲線隨著轉子長徑比的不同基本上沒有變化。表示在此偏心率范圍內，轉子系統的Op曲線趨于穩定不變，長徑比對系統穩定性的影響不明顯。當偏心率ε＞0.15時，圖5中的Op曲線將隨著長徑比的增大向上偏移，表示在此偏心率范圍內，轉子系統臨界轉速變小，穩定性也就越差。0等級當ε＜0.7時Op曲線向上偏移，表示在此偏心率范圍內當L∕D≠1時轉子系統臨界轉速變小，穩定性也就變差。即不同長徑比對滑動軸承運行穩定性的影響會因為存在圓柱度誤差而發生變化。

3.3 圓柱度誤差下長徑比對滑動軸承摩擦功率損耗的影響

為了研究圓柱度誤差下不同長徑比對功率損耗的影響，這里將摩擦損耗也導入計算公式中，不同長徑比下的摩擦功率損耗曲線，如圖4所示。觀察圖4可得，在12等級下當L∕D＜1時，轉子摩擦功率損耗曲線向左偏移，功率損耗下降；當L∕D＞1時，轉子摩擦功率損耗曲線也向左偏移，功率損耗下降。即存在圓柱度誤差時長徑比的增加和減小都會降低摩擦功率損耗。在0等級下隨著長徑比的增加，轉子摩擦功率損耗曲線向左偏移，功率損耗下降。即不同長徑比對滑動軸承摩擦功率損耗的影響會因為存在圓柱度誤差而發生變化。

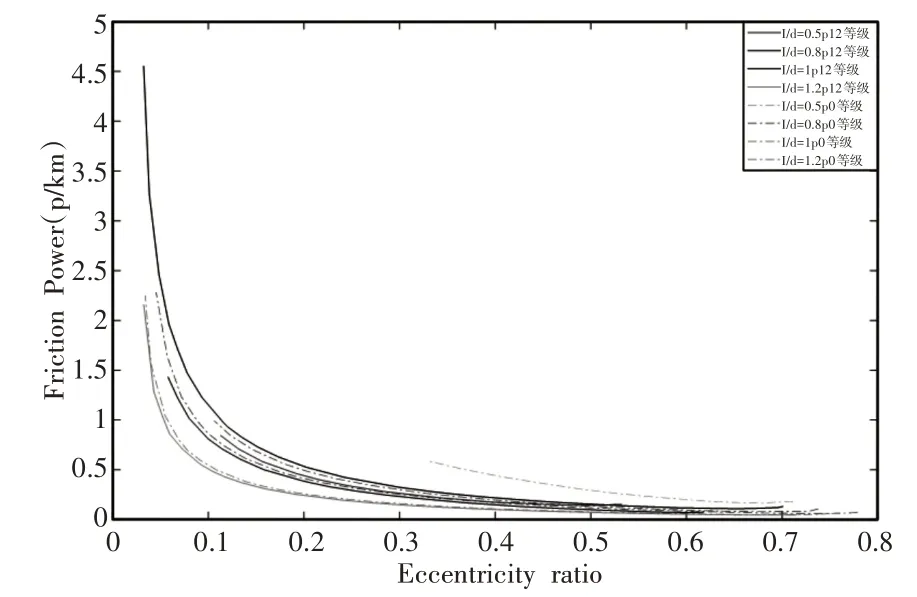
圖4 不同長徑比下軸承系統摩擦功率損耗與偏心率的關系Fig.4 Relationship Between Friction Power Loss and Eccentricity of Bearing System Under Different Length to Diameter Ratios

4 結論

（1）圓柱度誤差存在與否不改變長徑比對軸承承載能力的影響，即無論是否存在圓柱度誤差長徑比的增加都有利于承載力的提高。

（2）圓柱度誤差會改變長徑比對滑動軸承運行穩定性的影響。不存在圓柱度誤差時，當ε＜0.7時Op曲線向上偏移，表示在此偏心率范圍內當L∕D≠1時轉子系統臨界轉速變小，穩定性也就變差。存在圓柱度誤差時，當偏心率ε＞0.15時，Op曲線將隨著L∕D（0.5-1.2）的增大向上偏移，表示在此偏心率范圍內，轉子系統臨界轉速變小，穩定性也就越差。

（3）圓柱度誤差會改變長徑比對滑動軸承摩擦功率損耗的影響。不存在圓柱度誤差時隨著L∕D（0.5-1.2）的增加，轉子摩擦功率損耗曲線向左偏移，功率損耗下降。存在圓柱度誤差時當L∕D＜1時，轉子功率損耗曲線向左偏移，功率損耗下降，當L∕D＞1時，轉子摩擦功率損耗也向左偏移，功率損耗下降。