汽車發動機懸置系統與懸架系統集成控制研究

潘道遠，高清振，2，李寬路，李 偉

（1.安徽工程大學機械工程學院，安徽 蕪湖 241000；2.汽車新技術安徽省工程技術研究中心，安徽 蕪湖 241000）

1 前言

人們對車輛的整體品質追求日益提升，現代車輛正朝著安全、舒適、節能、環保、智能化的方向發展［1-3］。為了提高整車的綜合性能，考慮各個子系統之間的相互影響，進行集成控制已成為現代車輛控制研究的熱點［4］。文獻［5］為提高純電動汽車底盤的綜合性能，提出了一種實現純電動汽車復合制動與主動懸架協同控制方法。針對車輛極限工況下的穩定性問題，文獻［6］設計了一種四輪轉向和主動懸架的集成控制算法。

車輛懸置系統與懸架系統作為振動系統的兩個重要子系統，其振動的傳遞特性對操縱穩定性和乘坐舒適性有很大影響［7-9］。20世紀80年代開始研發的主動懸置能夠較好地滿足發動機理想的隔振特性，在低頻和高頻都具有良好的隔振效果。文獻［10］應用最優控制理論設計了主動懸置系統LQR控制器，并利用三種方法確定了控制器的加權系數。懸架系統是汽車的重要部件，其性能是影響車輛操穩性和舒適性的重要因素［11-13］。文獻［14］針對主動懸架系統的質量參數不確定性，提出了一種基于T-S模糊模型的主動懸架滑模容錯控制器設計方法。文獻［15］提出了具有擾動觀測器的滑模控制方法。針對電磁主動懸架直線式作動器電磁力波動對懸架系統影響問題，文獻［16］基于多目標粒子群算法對作動器結構參數進行優化。為實現更好的整體優化效果，文獻［17］對主動懸架的結構參數和控制器參數同時進行優化。

綜上所述，大部分研究集中于單個系統控制方法的研究，且控制效果較好，而對車輛懸置系統與懸架系統的集成控制研究相對較少。因此，這里以建立集成系統數學模型為研究切入點，應用最優控制理論設計集成控制系統，并采用粒子群算法優化加權系數以提高集成控制系統的控制品質。

2 集成系統數學模型的建立

采用復雜的多自由度整車模型設計出的控制器較為復雜，故這里對于車輛主動懸置系統與主動懸架系統的集成研究采用1∕4車輛簡化模型，如圖1所示。圖1中：m1—輪胎質量；m2—車身質量；m3—動力總成質量；k1—輪胎剛度；k2—懸架剛度；k3—懸置剛度；c2—懸架阻尼；c3—懸置阻尼；xq—懸架系統的路面輸入；x1—輪胎位移；x2—車身位移；x3—動力總成位移；fe—發動機自身產生的激振力；f1—主動懸架控制力；f2—主動懸置可控力。

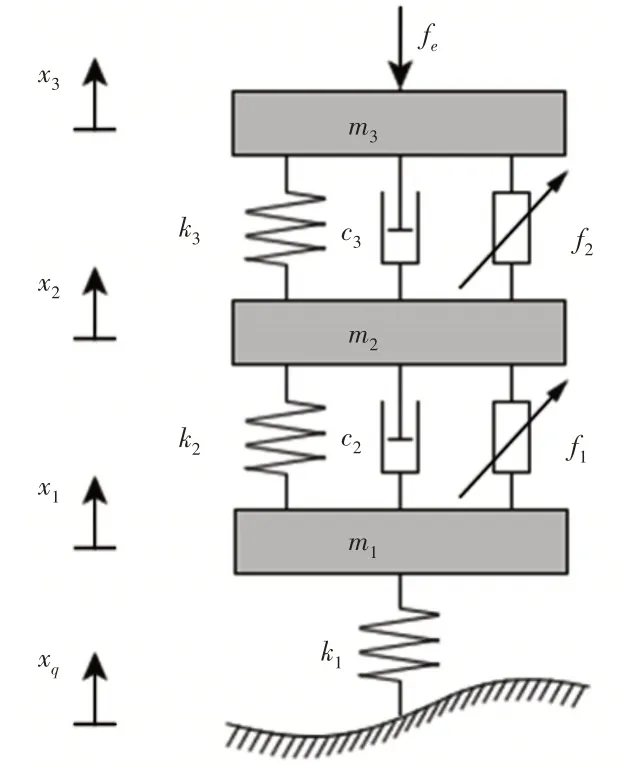
圖1 車輛懸置系統與懸架系統集成模型Fig.1 Integrated Model of Vehicle Mount System and Suspension System

對圖1中的集成模型進行動力學分析，可得到系統的微分方程為：

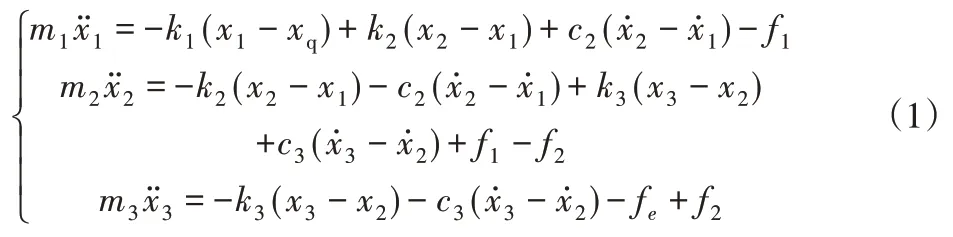
取狀態變量為：

輸出變量為：

則系統的狀態方程為：

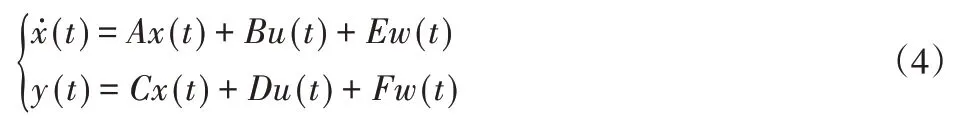
其中：

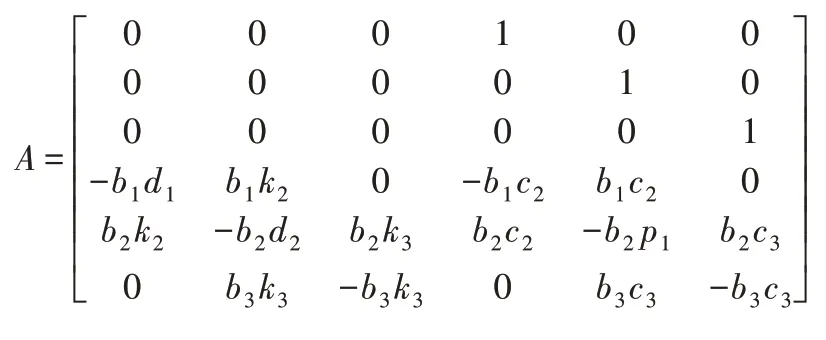
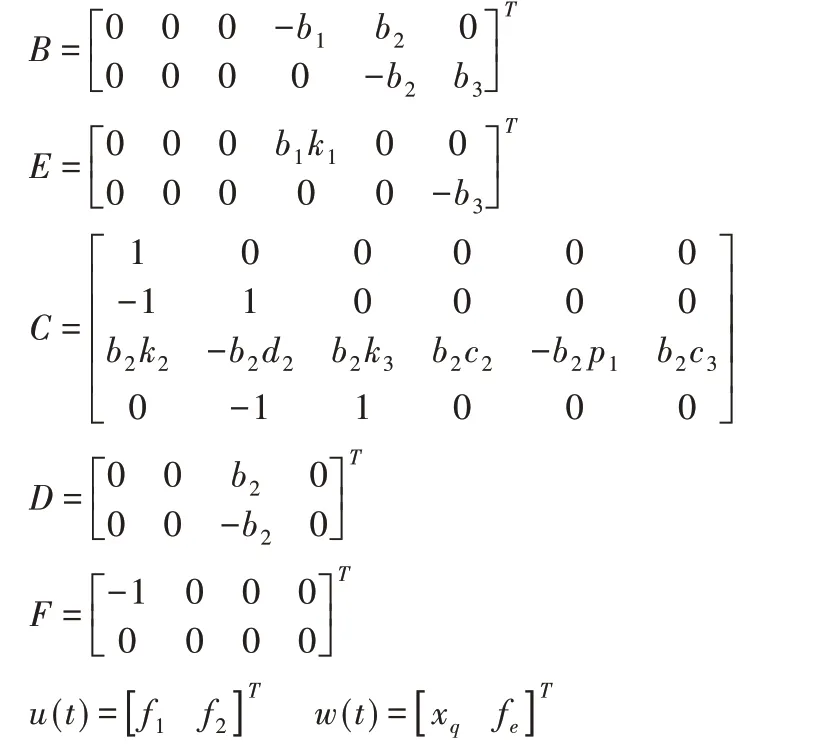
為了便于分析問題，路面激勵的時域模型采用濾波白噪聲模型［17］：

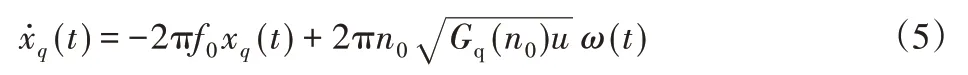
式中：f0—下截止頻率；n0—參考空間頻率；Gq（n0）—路面不平度系數；u—車輛行駛速度；w（t）—單位白噪聲信號。

在分析懸置系統的動態特性時，發動機激勵模型的建立是一個重要部分。直列四缸發動機的振動由二階往復慣性力產生［10］，其激勵模型為：

式中：φ—發動機安裝角；mp—單缸活塞質量；r—曲柄半徑；λ—曲柄半徑與連桿長度比；ω—曲柄角速度，ω= 2πn∕60，其中，n—發動機轉速。

3 集成系統控制模型

3.1 最優控制器設計

在集成控制系統的設計中，必須綜合考慮輪胎動位移、懸架動撓度、車身加速度及懸置動撓度。還要考慮主動懸架和主動懸置所耗能量盡可能小。因此，目標函數取為：

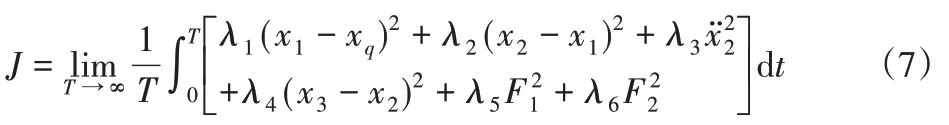
式中：l1～4—輪胎動位移、懸架動撓度、車身加速度和懸置動撓度的加權系數；l5和l6—主動懸架控制力和主動懸置控制力的加權系數。

根據LQR控制理論［10］，將式（7）改寫成二次函數積分型。

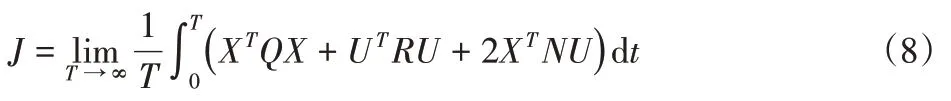
其中：

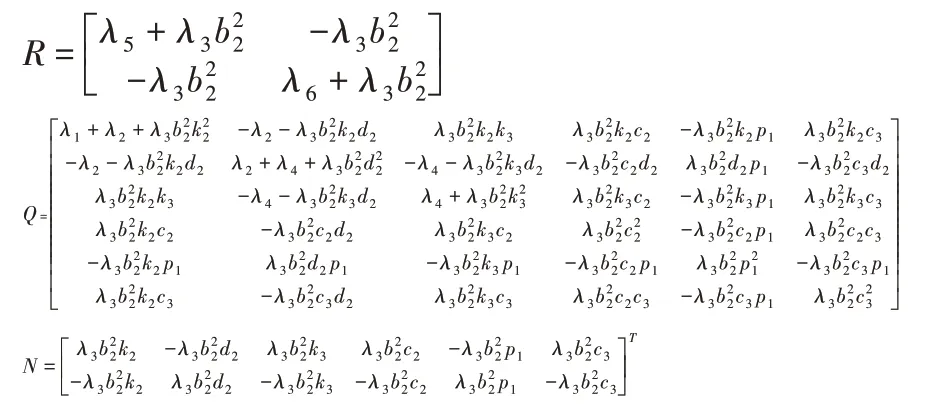
根據狀態變量x（t），可得出t時刻主動懸架和主動懸置輸出的最優控制力為：

其中，最優控制反饋增益矩陣K = BTP + NT，P矩陣滿足黎卡提（Riccatti）代數方程：

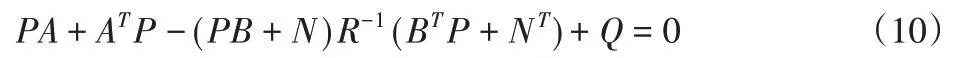
由上述LQR 控制主動懸置與主動懸架的集成模型可以看出，加權系數l1～4將對LQR控制車輛懸置系統與懸架系統的綜合性能產生重要影響，因此合理地選擇λ1～6是設計集成控制系統的關鍵之一。

3.2 粒子群優化算法

LQR控制器的加權系數確定需設計者依靠經驗反復調試，存在主觀因素，且系統難以得到期望的控制效果等問題。針對此問題，考慮利用粒子群算法優化加權系數以提高集成控制系統的控制品質。粒子群（Particle Swarm Optimization，PSO）算法是一種進化計算技術［4］。PSO算法首先進行初始化處理，然后在解空間中隨機生成粒子群。所有粒子由優化模型的目標函數來計算其適應值。粒子群在解空間中追蹤當前的最優粒子進行搜索，通過迭代找到最優解。假設在d維目標空間中搜索，生成的種群大小為N，第i個粒子的速度為vi =（vi，1vi，2…vi，d）、位置為xi=（xi，1xi，2…xi，d），其中，1 ≦i≦N。PSO算法將通過如下的公式更新粒子的速度和位置。

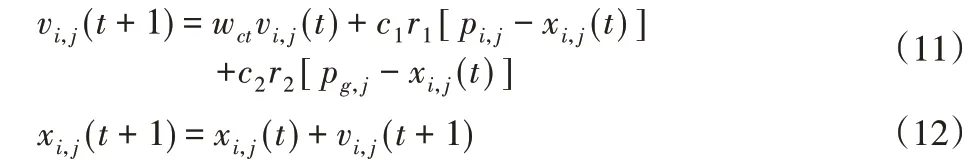
式中：j= 1，2，…，d；pi，j—第i個粒子自身所搜索到的最優解，其適應值為pbest；pg，j—粒子群當前搜索到的最優解，其適應值為gbest；wct—慣性權重；c1和c2—學習因子；r1和r2—（0～1）之間隨機數。

慣性權重對PSO算法的搜索能力有至關重要的影響。為平衡全局和局部搜索能力，慣性權重根據粒子適應值進行自適應調節。

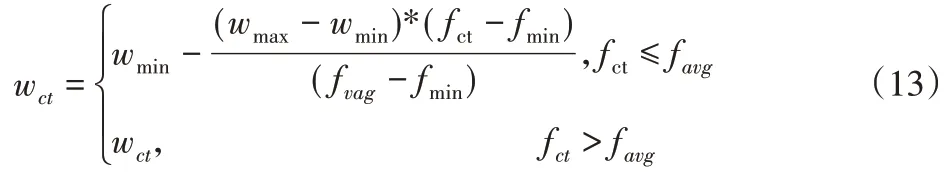
式中：wmin—慣性權重的最小值；wmax—慣性權重的最大值；fct—粒子當前的適應值；favg和fmin—所有粒子當前適應值的平均值和最小值。

3.3 集成控制模型

考慮到集成控制系統的性能指標輪胎動位移、懸架動撓度、車身加速度和懸置動撓度的單位和數量級的差異，將目標函數式（7）進行變換，采用集成控制系統相應指標的均方根值除以被動系統相應指標的均方根值作為粒子群算法的適應度函數，即：

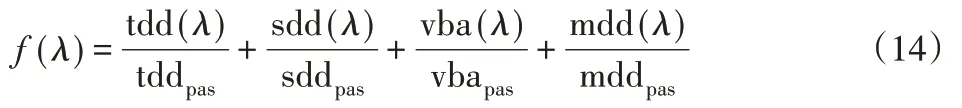
式中：λ =［λ1λ2λ3λ4λ5λ6］T，tdd（λ）、sdd（λ）、vba（λ）和mdd（λ）—輪胎動位移、懸架動撓度、車身加速度和懸置動撓度的均方根值；tddpas、sddpas、vbapas和mddpas—被動系統相應指標的均方根值。

考慮到集成控制系統的性能優于被動系統的性能，選取的約束條件為：

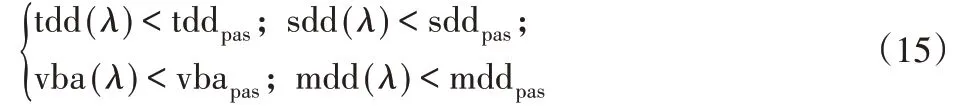
根據集成控制系統的目標函數和約束條件，采用Matlab 的PSO 工具箱對加權系數λ1～6進行優化。針對工具箱的核心函數pso_Trelea_vectorized 難于處理約束條件的問題，利用罰函數法將約束優化問題轉化為無約束優化問題［16］。同時，在優化λ1～6過程容易出現矩陣［Q N；NT R］非正定，從而導致調用lqr函數出錯，算法設計時進行了約束處理。改進PSO算法具體步驟如下：（1）初始化參數，隨機生成種群中各粒子的速度和位置。（2）將種群中各粒子的位置依次賦給LQR控制器的加權系數λ1～6。矩陣［Q N；NT R］非正定，令適應值fct=1000，退出（2）。計算最優控制反饋增益矩陣K和最優控制力U，并作用于集成控制系統。不滿足式（15）中任一約束條件時，令適應值fct=fct+1000，退出（2）。根據式（14）計算適應度函數，令適應值fct= f（λ）。（3）對種群中各粒子，將其適應值fct與其經歷過的最好位置pbest作比較，如果小于，則將其作為當前的最好位置pbest。比較當前所有pbest和gbest的值，如果小于，更新gbest。（4）判斷是否滿足PSO的終止條件。如果滿足，退出算法；否則，根據式（11）和式（12）更新粒子的速度和位置，根據式（13）更新權重，k=k+1，執行（2）。

根據上述改進PSO 算法步驟，編寫Matlab 優化程序。改進PSO 算法參數設定：粒子大小6，種群大小24，最大迭代次數2000，學習因子c1=c2=2，λ1～4的搜索范圍為［1，108］，λ5和λ6的搜索范圍為［10-8，1］，粒子最大速度為搜索范圍的10%。改進PSO算法優化過程中適應值迭代曲線，如圖2所示。由圖2可知，算法在前5次迭代中，矩陣［Q N；NT R］為非正定矩陣，適應值為1000。從第6次迭代開始到最大迭代次數2000為止，種群中粒子滿足約束條件，適應值由3.949減少到2.845，降低了27.96%。優化得到的加權系數λ1～6分別為7.61×106、3.24×106、6.25、108、0.003和6.73×10-4。

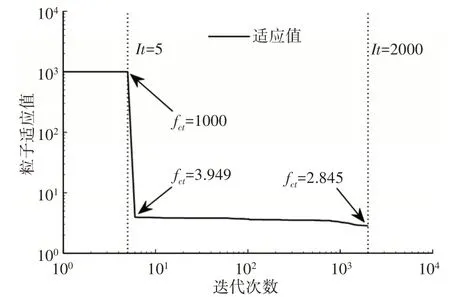
圖2 粒子適應值變化曲線Fig.2 The Changing Curve of Fitness Value of Particles

4 仿真計算及結果分析

為驗證車輛懸置系統與懸架系統集成控制采用基于粒子群算法優化的LQR控制策略的效果，與被動系統性能指標進行對比分析。選取集成控制模型仿真參數為：m1=25kg，m2=330kg，m3=56kg，k1=200000N∕m，k2=17000N∕m，k3=156000N∕m，c2=1900N·s∕m，c3= 1230 N·s∕m。首先在Matlab環境下進行頻域分析，得到性能指標對路面激勵的幅頻響應特性曲線，如圖4所示。路面激勵頻率的主要范圍為［0 10Hz］，見圖4中陰影區域。由圖4可知，在小于8.85Hz部分，基于粒子群算法優化的LQR控制（圖中為PSOLQR）與被動系統（圖中為Passive）相比，降低了輪胎動位移和車身加速度。PSOLQR 在大于2.67Hz 部分的懸架動撓度好于Passive，而在大于0.84Hz部分的懸置動撓度性能明顯好于Passive。綜上所述，車輛在路面頻率區域內采用基于粒子群算法優化的LQR控制的性能指標均有一定的改善。

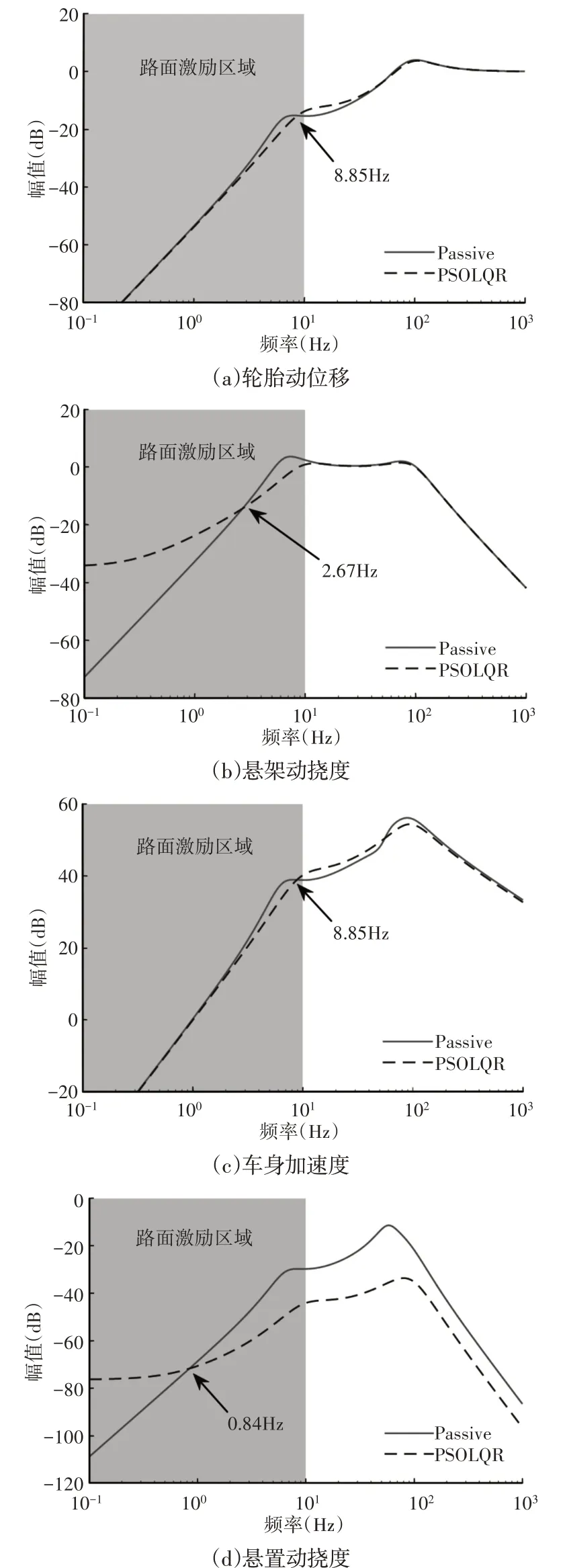
圖3 路面激勵下頻域仿真Fig.3 Frequency Domain Simulation under Road Excitation

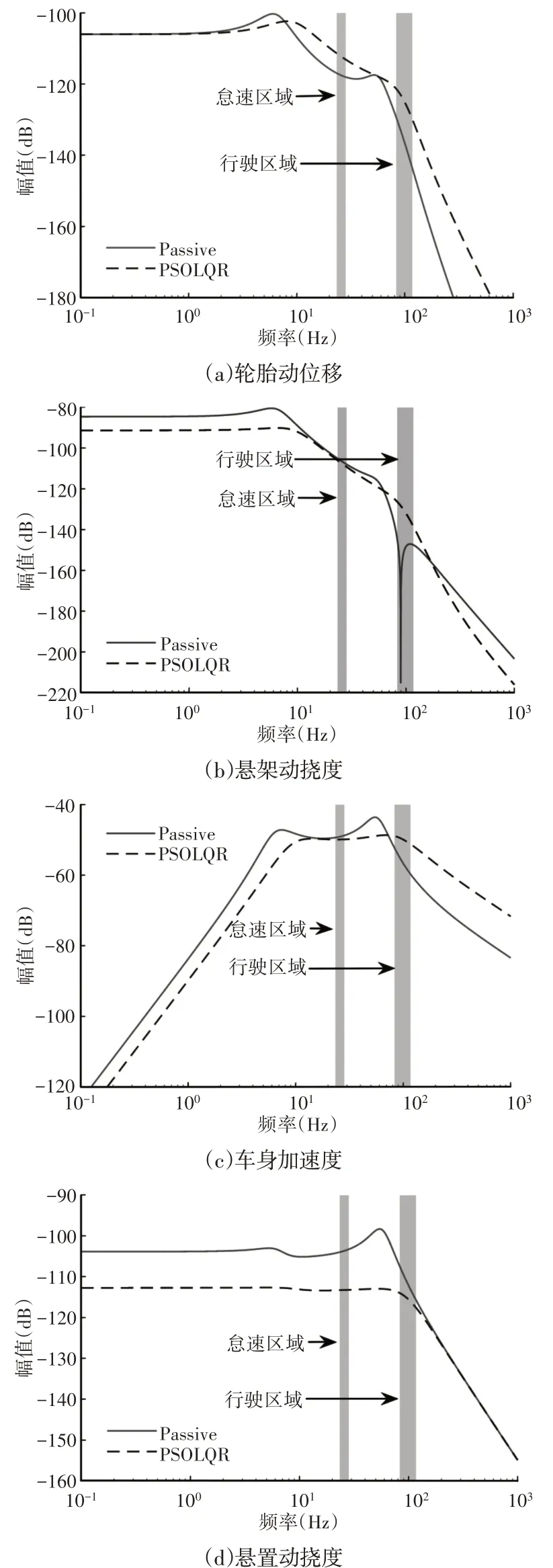
圖4 發動機激勵下頻域仿真Fig.4 Frequency Domain Simulation under Engine Excitation

性能指標在發動機激勵下的頻域仿真，如圖5所示。圖5中，發動機處于怠速區域時的轉速在700r∕min 到850r∕min 內波動，而處于行駛區域時的轉速維持在2500r∕min到3500r∕min。由圖5可知，PSOLQR在怠速區域與Passive相比，降低了懸架動撓度和車身加速度，顯著改善了懸置動撓度，這有利于發動機運行的穩定性，但輪胎動位移有所惡化。車輛此時處于靜止狀態，因此發動機激勵對輪胎動位移的影響有限。PSOLQR 在行駛區域與Passive 相比，僅懸置動撓度有所改善。車輛此時受到路面激勵和發動機激勵的聯合作用，相關性能指標受到雙重影響，因此需要從時域上進行詳細探討。

為進一步闡明車輛性能指標在路面激勵和發動機激勵聯合作用下的影響，在Matlab∕Simulink中搭建車輛懸置系統與懸架系統集成控制仿真模型進行時域分析，如圖5所示。圖5中，路面激勵根據車速和路面等級給出，而發動機激勵由發動機轉速決定。車輛行駛時在路面激勵和發動機激勵聯合作用下產生振動，從而影響其乘坐舒適性和操縱穩定性。集成控制系統首先通過車載傳感器實時采集車輛運行狀態信息，然后經ECU采用LQR控制算法計算所需控制力大小，最后由主動懸置和主動懸架輸出相應控制力，從而抑制車輛的振動，使NVH綜合性能達到最優。假設車輛在B級路面上行駛，路面不平度系數G0= 64×10-6m2∕m-1，車速u=20m∕s，發動機轉速n=2500r∕min。車輛在路面激勵和發動機激勵聯合作用下主動懸架控制力和主動懸置控制力，如圖6、圖7所示。由圖6和圖7可知，主動懸架和主動懸置輸出的最大控制力分別為708N和585N。主動懸置控制力幅值變化頻率遠大于主動懸架控制力，這說明在產品設計時要求主動懸置的響應速度更快。

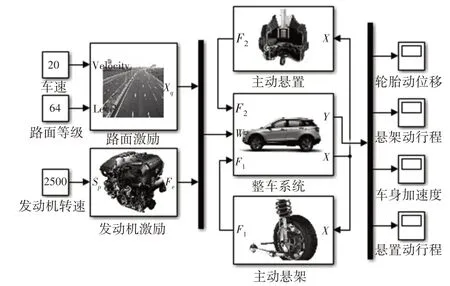
圖5 集成控制仿真模型Fig.5 The Simulation Model of Integrated Control System

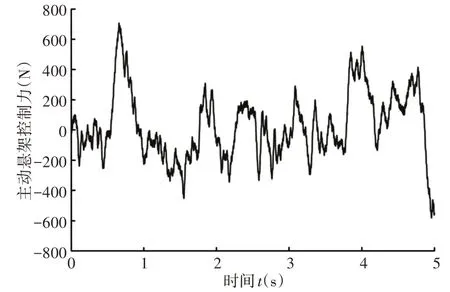
圖6 主動懸架控制力Fig.6 The Control Force of Active Suspension

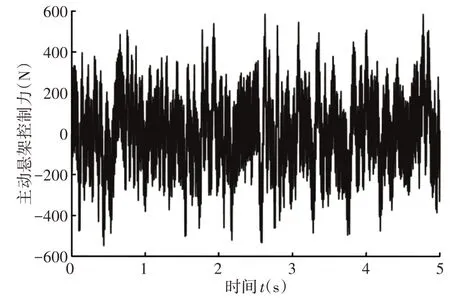
圖7 主動懸置控制力Fig.7 The Control Force of Active Mount

車輛在路面激勵和發動機激勵聯合作用下的動態特性，如圖8所示。

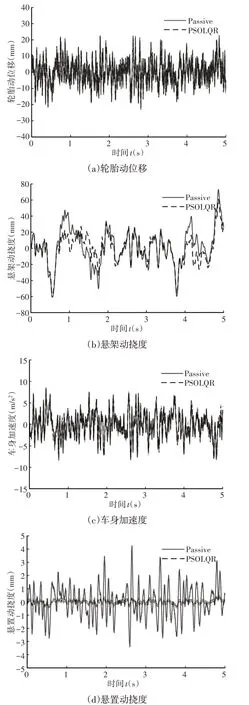
圖8 路面與發動機聯合激勵下時域仿真Fig.8 Time Domain Simulation under the Joint Excitation of Road and Engine

由圖8可知，輪胎動位移的峰值和均方根值分別由22.8mm減小到22.6mm和7.4mm減小到7.3mm，降低了0.88% 和1.35%。懸架動撓度的峰值和均方根值分別由73.1mm減小到61.2mm和23mm減小到18.6mm，降低了16.28%和19.13%。車身加速度的峰值和均方根值分別由8.51m∕s2減小到8.28m∕s2和2.86m∕s2減小到2.79m∕s2，降低了2.7%和2.45%。懸置動撓度的峰值和均方根值分別由4.3mm 減小到0.5mm 和1.2mm 減小到0.2mm，降低了88.37% 和83.33%。上述數據說明基于粒子群算法的LQR 控制策略在改善懸架動撓度和懸置動撓度方面效果明顯，有利于提高車輛的操縱穩定性，但在改善乘坐舒適性不足。由目標函數式（7）可知，車輛性能指標之間是存在矛盾的。為進一步協調車輛的操縱穩定性和乘坐舒適性，將在后續研究中探索根據車輛行駛工況和發動機運行狀態進行混雜控制。

5 結論

建立了車輛懸置系統與懸架系統的集成模型，基于最優控制理論設計了集成控制系統。針對最優控制器加權系數難以確定的問題，采用粒子群算法優化加權系數以提高集成控制系統的控制品質。為驗證集成控制系統采用基于粒子群算法優化的LQR控制策略的效果，在Matlab環境下進行了頻域分析，分析表明車輛在路面頻率區域內采用基于粒子群算法優化的LQR控制的性能指標均有一定的改善。為進一步闡明車輛性能指標在路面激勵和發動機激勵聯合作用下的影響，在Matlab∕Simulink中搭建集成控制仿真模型進行了時域分析，分析表明基于粒子群算法的LQR控制策略在改善懸架動撓度和懸置動撓度方面效果明顯，有利于提高車輛的操縱穩定性，但在改善乘坐舒適性不足。為進一步協調車輛的操縱穩定性和乘坐舒適性，將在后續研究中探索根據車輛行駛工況和發動機運行狀態進行混雜控制。