“指向數學建模素養的可視化學習”的課堂實踐

江蘇省無錫市堰橋高級中學 郭桂霞

橢圓標準方程是人教版選修性必修第一冊內容，分為兩個課時，“橢圓標準方程”第一課時是學生學習了直線方程、圓的方程之后的后繼知識，學生已具有一定的觀察、分析和解決一些相關問題的能力。而推導橢圓的標準方程的方法對雙曲線、拋物線方程的推導具有直接的類比作用，為學習雙曲線、拋物線內容提供了理論基礎和基本模式，是一個重要的數學建模示范。本文從知識導入、知識建構、知識運用三方面教學實錄與評析談談如何在教學中通過設置適當的問題啟發、引導學生思考，提升學生思維，主動建構模型，提升數學素養。

一、知識導入

情境1：播放“嫦娥五號”探測器發射升空的視頻，當屏幕上出現探測器運行的軌跡時，學生齊聲呼喚軌道是橢圓。

（評析：背景材料緊跟時代步伐，迅速抓住學生的注意力，能讓學生觸景生情，激發探索熱情，認識到建模的必要性，讓學生感受數學從生活中來，數學服務于生活。）

情境2：幾何畫板展示圓被壓扁的過程

生眾：橢圓。

師：以上圖形從感性上看都給我們橢圓的印象，從數學理性的角度上看，它們是嚴格意義上的橢圓嗎？為了進一步研究橢圓，我們將利用解析幾何的思想，用代數的方法來研究幾何問題，所以我們要研究橢圓的方程，這就是我們要研究的課題：橢圓的標準方程。

（評析：設置情境,引入疑惑,激發學生對問題的思考與反思，給出研究課題的必要性。讓學生能從數學的眼光思考問題，培養思維的嚴密性。）

二、知識建構

師：如何求橢圓方程？關于橢圓你有哪些了解？

生眾：橢圓定義。

（評析：讓學生能主動地根據先前認知結構，有選擇性地知覺外在信息，讓思維有增長的起點。）

師：橢圓的定義是什么？

生1：平面內到兩定點FF的距離的和等于常數的點的軌跡叫做橢圓。

師：常數有要求嗎？

生2：常數2a必須大于FF。

師：為什么？

生3：如果常數等于FF，軌跡為線段FF；若常數小于FF，軌跡不存在。

（評析：讓學生了解知識的內涵與外延，這是思維增長的必經過程。）

師：我們不會求橢圓的標準方程，回顧一下如何求出圓的標準方程。

生4：建立坐標系、設點、找等量關系、代入坐標、化簡。

（評析：通過復習舊知識，并采用同化法，喚起學生對數學思想方法的提取，從而找到了知識的“生長點”。）

師：求橢圓標準方程，如何建立適當的坐標系？

生5：以FF所在直線為x軸，以過F與FF垂直的直線為y軸。

生6：以FF所在直線為x軸，以FF中垂線為y軸。

師：有兩種建系的方法，大家覺哪個更好呢？為什么？

生7：第二個，圖形更對稱，感覺后面的運算可能更簡單一點。

（評析：尊重學生思路，發揮學生主體性，并讓學生學會思考思路的合理性與思路的優化、能優化的原因，培養學生思維的不斷深入。）

（1）建立適當的坐標系：以直線FF為x軸，線段FF的垂直平分線為y軸，建立如圖所示的坐標系。

（2）設點P(x,y)：設是橢圓上的任意一點,FF=2c，F(-c,0),(c,0)。

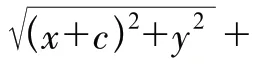
師：如何化簡這個方程呢？大家可討論討論。

生8：直接兩邊平方；

生9：移項后兩邊平方；師：我們選哪種方法？生10：第二種，一邊一根式，對稱一些。

（評析：前面建系的對稱性已在學生思維里有了意識，主動去優化方法，思維有所增長。）

在黑板上用方案2加以推導。在化簡得出方程(a-c)x+ay=a(a-c)后師：能否把式子寫得更簡潔些？

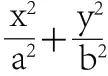
師：大家觀察式子的特征，若x，y是一次的話，是什么曲線的方程？

生11：直線的截距式方程。

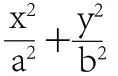
生12：與x軸的交點為(-a,0)，(a,0)，與y軸的交點為(-b,0)，(b,0)。

師：一次是直線，二次是曲線表示橢圓，數學很奇妙。

（評析：滲透了自然美、對稱美、簡潔美，幫助學生記憶橢圓標準方程。）

師：這里a，b，c的等量關系和大小關系如何？

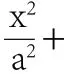
師：那么方程是否會具有對稱性呢？

生13：好像有，x，-x分子是平方，的平方一樣，y，-y的平方一樣。

它表示焦點在x軸上的橢圓，a是最大的（既然b=a-c，那么我們是否能在圖中找到以a,b,c為邊的直角三角形呢？結合圖形發現△OFB）

（評析:讓學生從數的角度感受到對稱性，體會形與數的統一。）

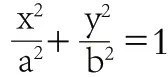
生眾：圓。

（評析：從代數的角度觀察橢圓與圓的區別，對情境2的直觀感知的嚴謹化。）

師：橢圓可圓可扁，焦點在軸上的橢圓該如何表示？

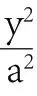
（評析：類比焦點在軸上的橢圓，讓學生利用已有知識,在做中學,類比學,并把新知識同化到原有知識。）

三、知識運用

例1：判斷下列橢圓的焦點在哪個軸上，并寫出焦點坐標：（過程略）

師：能幫我們總結一下求焦點的方法嗎？

生15：先化成標準方程，再看分母大小確定焦點位置，再利用c=b-c求出，得到焦點坐標。

（評析：通過具體實例讓學生能根據分母的大小判斷焦點位置，會求橢圓方程中的基本量a,b,c的方法。）

變式：求適合下列條件的橢圓標準方程：

（1）焦 點 是F(-2,0)，F(2,0)且過點P(2,3)。（2）焦距為4，且過點P(2,3)。

師：對于（1），你能說出解題思路和主要過程嗎？

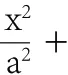
生17：2a=PF+PF,直接求出a，c=2，b=a-c求出b。

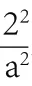
（評析：掌握求橢圓標準方程常用的思想方法——定義法和待定系數法；求橢圓標準方程時，焦點位置不確定，能主動分類討論。）

例2：已知一輛運油車上的儲油罐截面的外輪廓線是一個橢圓，它的焦距為2.4m，外輪廓線上的點到兩個焦點之和為3m，求這個橢圓的標準方程。(過程略)

（評析：與課程導入相呼應，解決實際問題。讓學生能用數學的眼光觀察世界，用數學的思維分析世界，讓學生面對實際問題時，能用數學的思維去分析、建立模型并解決。）

教學反思：本課是圓錐曲線的方程的起始課，通過在課堂上讓學生直觀感受橢圓形狀，判斷橢圓的方法，讓學生感受直觀的不足、研究橢圓方程的必要，讓學生的思維從具體到抽象，從淺層到深入，思維的發展可視化。在研究未知的橢圓方程時，引導學生回顧已學的圓的方程的求法，主動類比研究橢圓,培養學生數學建模意識。橢圓方程出來后,讓學生從數與形兩個角度感受對稱性，體會數學形與數的統一，感受數學的美，讓學生能在后續的雙曲線中主動尋找數學的美，培養學生從數學的角度發現美并創造美的能力，感受大自然美的同時能嘗試用數學建模的思想給予美的詮釋。

數學是一種思維活動，數學教育是思維的教育。在知識的導入與生成過程中，通過設置高質量的問題，讓學生充分思考，尋求思路的合理性，主動優化思路，讓思維的增長有土壤，教師搭好腳手架，引導學生利用已有知識，在做中學，類比學，引導學生思維不斷走向深入，提高學生數學素養。