空域預先規劃時間的沖突處理方法研究

高志周，萬路軍，鐘 赟，蔡 明，徐鑫宇

(1.空軍工程大學 空管領航學院， 西安 710051； 2.空軍工程大學 裝備管理與無人機工程學院， 西安 710051； 3.中國人民解放軍94040部隊， 新疆 庫爾勒 841000)

1 引言

空域的使用需要在嚴格的時間約束下執行，但在劃設空域過程中，由于作戰任務需求不同，同時受到惡劣天氣、環境變化的影響，空域使用需求會在時間上產生沖突，從而造成作戰任務的沖突。為保證空域使用安全，需要對空域時間進行約束。

當前，眾多學者對空域沖突檢測及消解開展了研究，毛億等提出了一種空域沖突快速檢測的方法，采用“由粗到精，逐步排除”的方法對空域時間、垂直方向、水平維度上逐步進行沖突檢測；楊毅等提出了基于柵格模型的大規模空域使用計劃沖突檢測與解脫方法，根據空域使用計劃將空域柵格化并編碼，建立空域網格內置屬性并判斷計劃沖突空域；龔瑋等提出一種基于柵格模型的空域沖突檢測解脫技術，對大量空域使用計劃之間的空域沖突進行檢測及解脫。

以上學者對空域使用沖突進行了研究，目前對于空域預先時間沖突的處理方法主要采用以甘特圖為基礎對作戰任務時間區間進行逐一比對，從而發現時間沖突，這種方法具有計算效率低、計算不精確、復雜性低等缺點。而簡單時間網絡(simple temporal network，STN)是一種可以表示時間約束的模型，具有計算簡便、使用靈活等特點，適用于對空域預先規劃時間沖突的處理。

對STN的應用方面，也有許多學者進行了深入研究，湯羅浩基于STN對行動計劃時間的表示和沖突處理開展了研究，設計了迭代檢測沖突和消解的CDR算法；李娟提出并實現了一種基于STN的時間、空間、資源沖突檢測和消解算法；李遠等提出了基于最小沖突集的沖突檢測算法，在此基礎上設計了基于最小承諾的沖突消解算法；謝斌等設計了一種基于STN的任務在執行過程中資源沖突自動消解的方法。以上研究均以行動計劃為背景，利用STN對計劃時間進行了時間一致性檢測及消解，為空域的時間沖突檢測及消解提供了一種新的思路。

在制定空域使用計劃時，對時間有很強的約束要求，首先需要在時間層面進行沖突檢測和消解，而STN以圖論形式滿足時間約束來檢測和消解空域之間的時間沖突，相比傳統的時間沖突判斷方法，具有計算快速的特點。對此，本文提出基于STN對空域預先規劃時間沖突處理。

2 空域預先規劃時間建模

STN是一種針對計劃執行的時間約束網絡，基于空域的起始和結束時間、任務時間、活動執行順序等要素，可以畫出STN圖。在空域劃設過程中，根據提交的空域使用需求，對空域添加時間約束，將空域使用轉化為計劃執行，得到基于空域使用需求的STN。STN由點時間變量集和事件約束集表示，中的元素是各點時間變量，表示事件的開始結束時刻，由約束不等式構成，表示事件之間的時間約束關系。

STN中利用有向約束圖=(，)構成時間約束網絡，網絡中的頂點集合表示點時間變量集，邊集合表示時間約束集。頂點和連接的弧→表示時間約束。→∈[，]表示事件和事件滿足時間約束，≤-≤(和均為時間)表示在至少后發生，且最多不超過前發生。時間沖突檢測實質是判斷時間約束網絡一致性，如果行動方案滿足所有的時間約束，則稱STN滿足一致性，否則表明方案存在時間沖突。一般在處理過程中，將STN轉化為STN距離圖，即有向加權圖=(，)，將時間約束≤-≤轉化為權值為的弧→，以及權值為-的弧→，更加便于計算，如圖1所示。

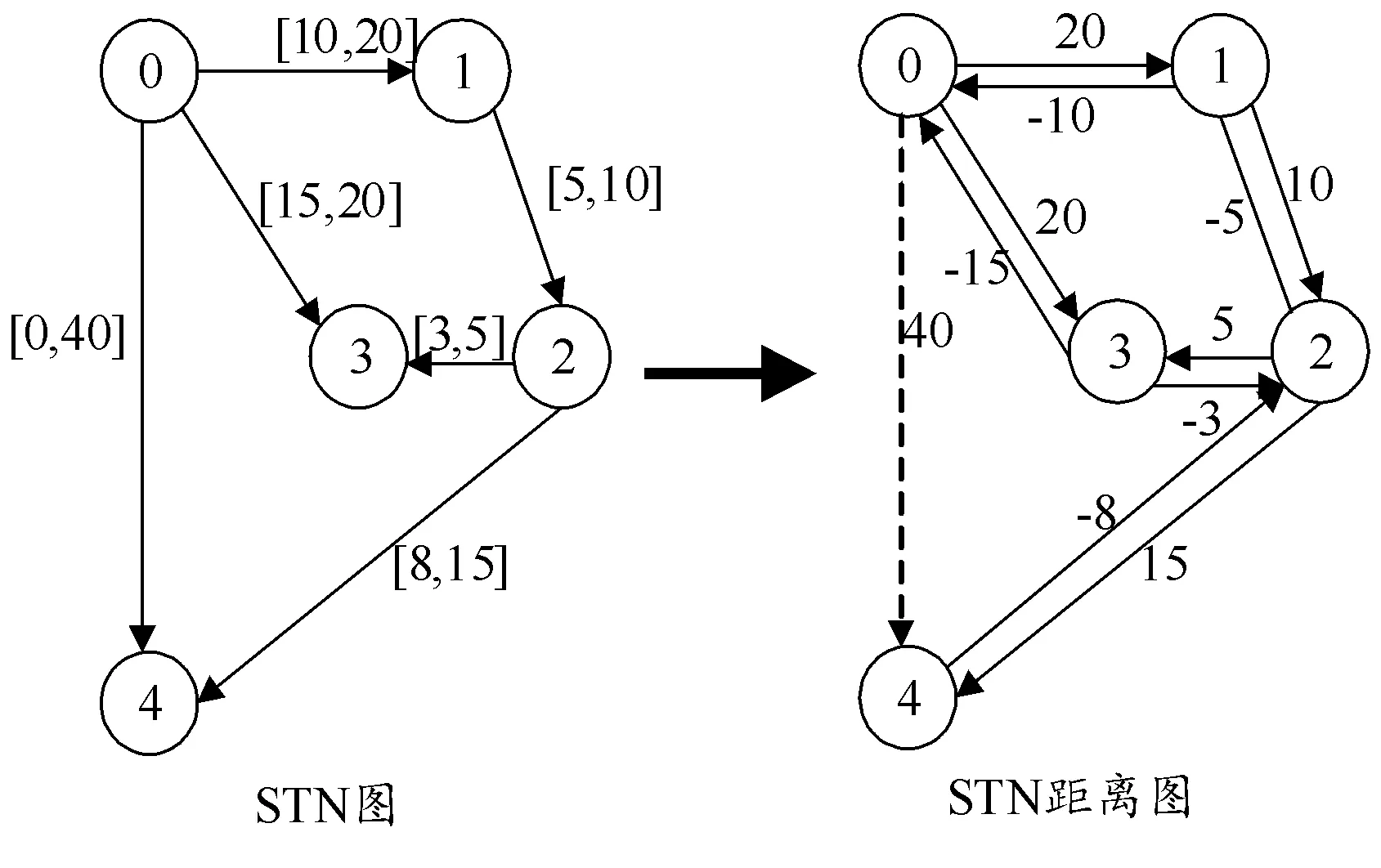
圖1 STN圖與STN距離圖的轉換示意圖

2.1 預先規劃時間約束網絡表達

對空域時間沖突的處理，首先對空域使用計劃進行系統性的表達，從用空行動的角度分析，空域使用計劃可表示為：

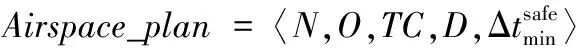
在時間約束中，用時間點和時間區間來共同描述空域時間，時間點表示在某一時刻或短時間內的空域內的用空行動，時間區間表示在一定時間范圍內的用空行動，即空域的使用時間范圍，時間區間可由和分別來表示空域使用時間的開始時刻和結束時刻。

為了便于計算需要將時間點和時間區間的定性約束關系轉換為定量約束關系，如表1所示。

2.2 時間沖突檢測流程

對空域使用時間進行沖突檢測前，首先對空域使用計劃和時間約束網絡構建數學模型，以定量不等式的形式進行表示，并構建STN距離圖。利用最短路徑快速算法(shortest path faster algorithm，SPFA)算法對STN距離圖進行負環檢測，檢測流程如圖2所示。

表1 定性約束轉換為定量約束

圖2 時間沖突檢測流程框圖

在時間沖突檢測中，首先制定空域使用計劃，根據空域使用計劃的要素，構建時間約束網絡，即STN圖，再將其轉換為STN距離圖，將時間沖突問題轉化為圖論的一致性檢測問題，利用SPFA算法對STN距離圖進行負環檢測，若存在負環，則有向圖中存在沖突，即空域使用計劃存在時間沖突。

2.3 SPFA算法

最短路徑快速算法(shortest path faster algorithm，SPFA)是求解單源最短路徑的算法之一，其原理是對圖進行-1次松弛(為圖中頂點數)，得到源點到所有頂點可能的最短路徑，相較于常用的最短路徑算法Bellman-ford和Dijkstra算法，SPFA算法可以在負權圖中進行計算，缺點是時間復雜度更高。SPFA算法用一個數組來記錄各個結點的最短路徑估計值，首先設立一個先進先出隊列(FIFO)，每次優化時取出隊首結點，同時點的最短路徑估計值對離開點所指向的結點進行松弛，如果點的最短路徑估計值有變化，且點不在此FIFO中，將點放到隊尾。以此類推，不斷從隊列中取結點進行松弛操作，直到隊列為空時，停止操作。如果某個結點出隊列的次數大于等于次，則存在負環(為圖的頂點數)，SPFA算法檢測流程如圖3所示。

SPFA算法中的松弛和Bellman-ford算法中對同一個點的松弛一樣，Bellman-ford算法是求解最短路徑的算法，最短路徑是一條路徑必然不是一個環，在有條邊的有向圖=(，)中，路徑的最大長度為-1，因此當迭代次數大于等于時，說明存在負權環，因此在SPFA算法中若某頂點出隊次數大于等于，則存在負權環。

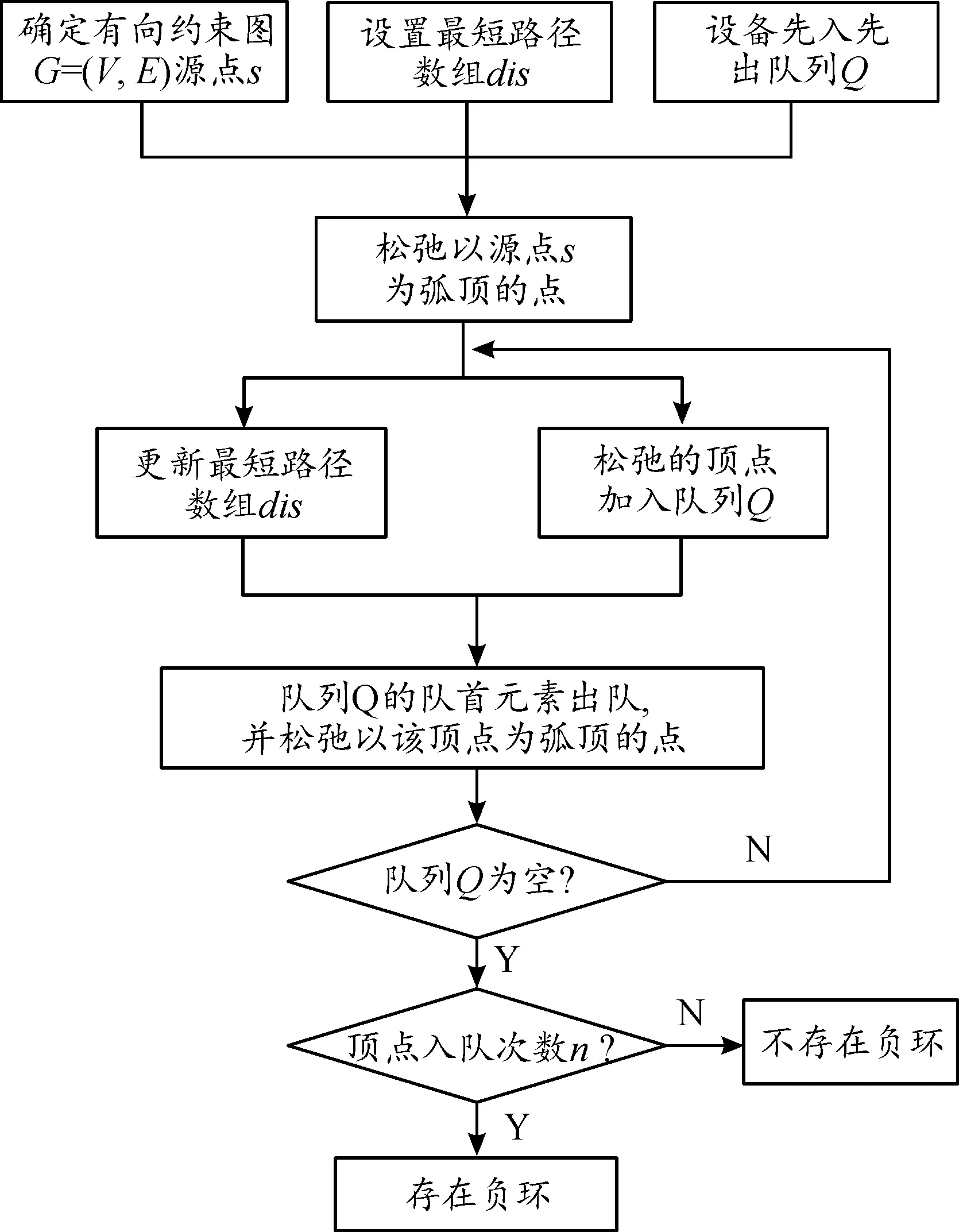
圖3 SPFA負環檢測算法流程框圖

以圖4為例，首先確定有向約束圖=(，)的源點，將賦值為0，其余頂點賦值為+∞，得到初始化數組(=0，=+∞，=+∞，=+∞，=+∞)，同時將加入隊列中，此時={}；繼續之前的循環，第1次循環時，的隊首元素出隊列，即出隊列，對以為弧頂的點進行松弛，到，的最短路徑縮小，更新數組(=0，=-1，=4，=+∞，=+∞)，可以看到、之前不在隊列中，將他們入隊列，此時先入先出隊列為={，}。

進入第2次循環，隊首頂點出隊列，對以為弧頂的點進行松弛，可以看到到、、的最短路徑縮小，更新數組得到(=0，=-1，=2，=1，=1)，同時、不在隊列中，將其加入隊列，此時先入先出隊列為={，，}。

用上述方法不斷迭代更新數組和隊列，循環迭代至數組為(=0，=-4，=-1，=-5，=-1)時，此時出隊列5次，可以判斷出圖4存在負環→→→。

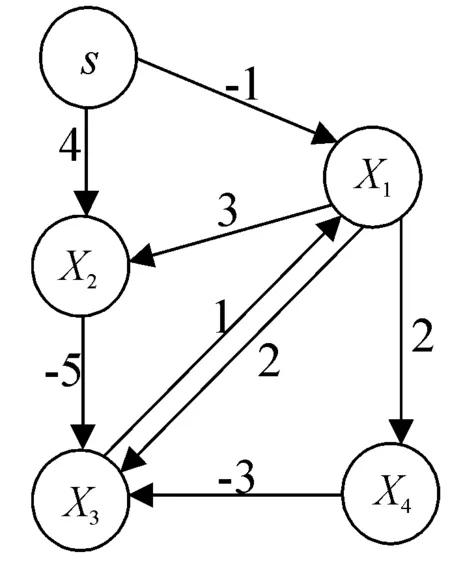
圖4 有向約束示意圖

2.4 基于前驅節點數組的改進SPFA算法

2.3節中對SPFA算法的優點和算法流程進行了描述，在圖3中通過記錄頂點的出隊次數判斷圖中是否存在負環，而在計算過程中有多次多余的入隊操作，增加了計算的復雜性，沒有及時輸出負環判斷結果。迭代循環輸出數組是基于尋找最短路徑來記錄松弛變化的，而在負環檢測方面可以定義一個記錄各頂點的前驅節點數組，通過對該數組中的頂點關系進行描述來判斷是否存在負環，當某頂點沒有前驅節點時用-1表示，改進算法流程如圖5所示。

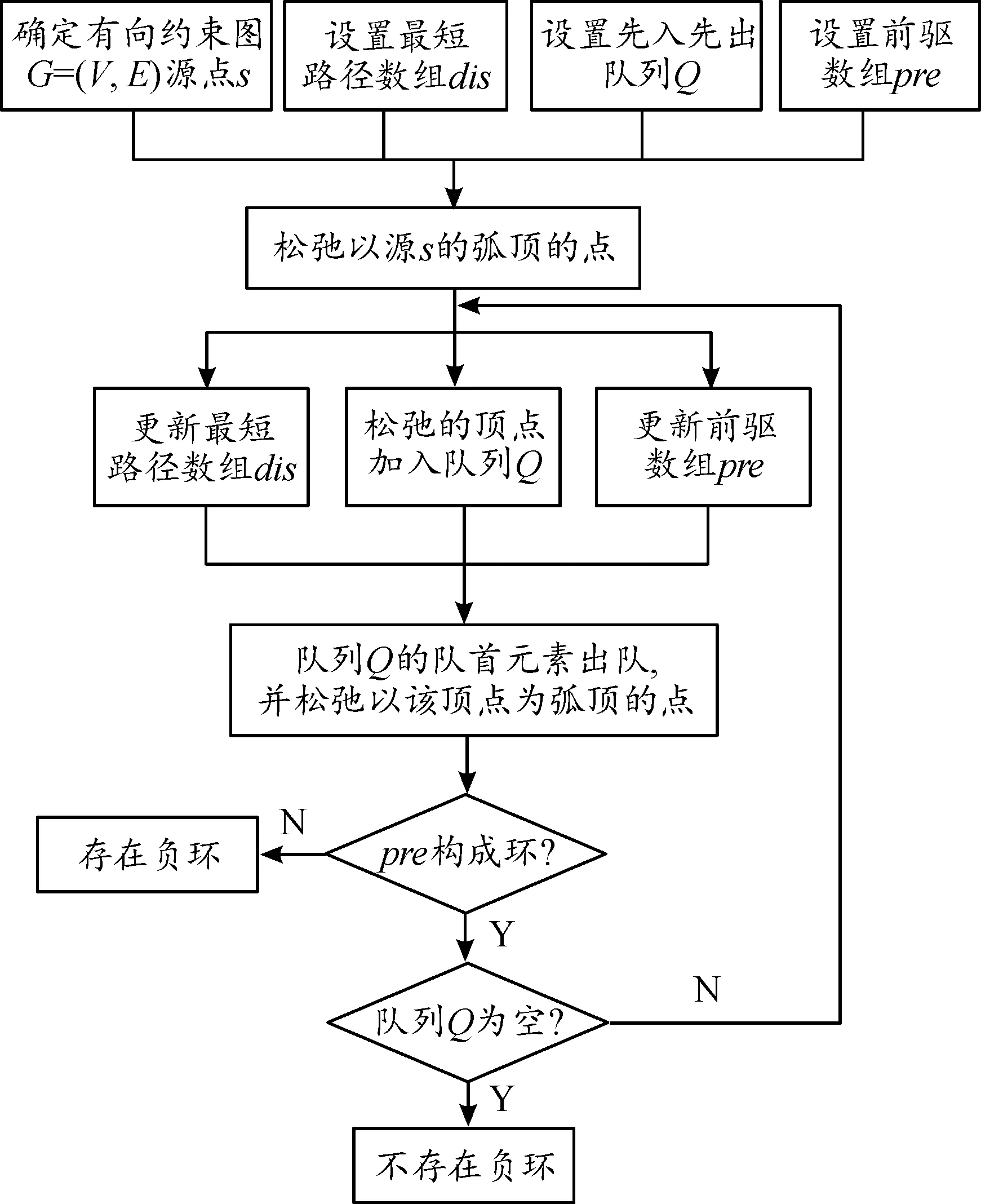
圖5 SPFA負環檢測改進算法流程框圖

在圖5中，第1次循環時出隊，數組為(=0，=-1，=4，=+∞，=+∞)，此時的前驅節點數組(=-1，=0，=0，=-1，=-1)；第2次更新數組(=0，=-1，=2，=1，=1)，此時(=-1，=0，=1，=1，=1)，按照同樣的方式松弛約束，到第4次循環時出隊，此時的數組更新為(=0，=-2，=2，=-3，=1)，前驅節點數組更新為(=-1，=3，=1，=2，=1)，此時出現死循環，即可判斷圖中存在負環→→→。

相較普通的SPFA算法，本節提出的方法通過4次循環中就找到了負環，大大提升了計算效率，減少了不必要的入隊和出隊操作。

3 時間沖突消解

3.1 負環消解流程

在STN圖中出現負環后需要對負環進行消解，由于出現負環意味著存在時間沖突，因此對負環進行消解的過程就是調整時間約束的過程。

調整約束包括松弛約束、加緊約束、刪減約束、添加約束；加緊約束和添加約束會使約束程度更高，不適用于空域時間的沖突消解方面。刪減約束是極端的松弛約束，以刪除部分約束來達成時間一致性，但同時會影響任務的完整性。因此，利用松弛約束對負環進行消解。

在列出了某作戰行動的各類時間約束后，在對任務完成影響最小的前提下進行松弛約束，對約束添加代價系數，表示調整該約束需要付出的代價，再按照優先選擇代價最小的約束進行松弛。

3.2 基于最小代價的負環消解

在負環的消解中，將負環權值-加上權重可以消解負環，但會導致事件發生的時間相對固定，缺少了STN圖的靈活性，因此對負環權值-加上權重+(>0)，為靈活因子。

對權值為負的弧進行松弛約束時，不能將其權值調整為正值，例如權值為(<0)的弧→表示事件在事件后個單位時間發生，若對權值進行調整使得>0則表示先于至少個單位時間發生，變換了事件的發生順序，因此對權值為負的弧進行調整時，不能使其權值大于0。

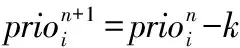
綜上所述，可得到調整代價函數為：

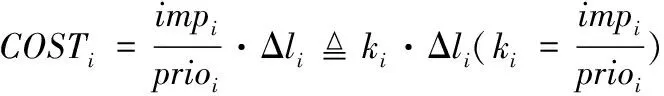
式(2)中：Δ表示約束的變化量；為代價系數。

對由條弧構成的負環進行消解時，基于最小代價的目標函數為：

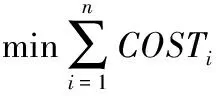
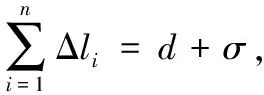
檢測到負環后采用貪心算法，尋找代價最小的約束盡可能大的增加權值，到其無法增加后尋找代價次小的約束進行調整，直到負環消解，基于最小代價的負環消解算法流程如圖6所示。

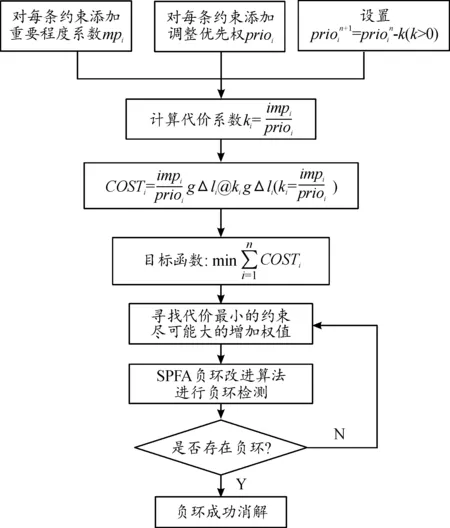
圖6 基于最小代價的負環消解算法流程框圖

4 實例分析

某年某月某日，開展遠程火力打擊訓練任務，1編隊擔負火力突擊任務，2編隊擔負空中加油任務，3編隊擔負對目標區域空情偵察任務，4編隊擔負攔截敵突擊任務。區域A為敵入侵空域，區域B為我方攔截空域，區域C為我方機場空域。打擊訓練任務流程如圖7所示。

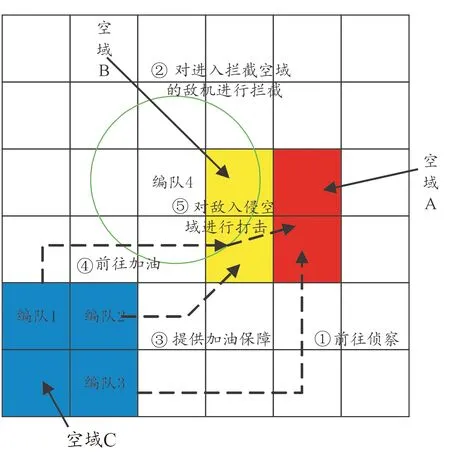
圖7 打擊訓練任務流程示意圖

任務流程為：上午8時，3編隊前往區域A對敵空中力量進行偵察，偵察完畢后返回并上傳情報，4編隊接收情報后向區域B進行攔截攻擊，4編隊攔截結束后，2編隊由區域C前往區域B，同時1編隊由區域C前往區域B加油，完成加油后 1編隊前往區域C對目標進行火力突擊，規定8時32分前完成任務。

根據上述任務流程得到時間約束,見表2。

表2 任務時間約束

1編隊前往加油區需要3～5 min，加油過程需要5～7 min，加油完成后到達目標區域需要6～10 min，完成對目標的攻擊需要1～2 min，2編隊前往加油區需要8～10 min，加油過程需要5～7 min，3編隊到達指定區域需要5～8 min，偵察過程需要6～9 min，發現敵方并上傳情報需要3～4 min，4編隊準備架設需要5～8 min，實施攔截需要6～7 min。整個行動時間不得超過35 min。打擊行動的STN圖如圖8所示。

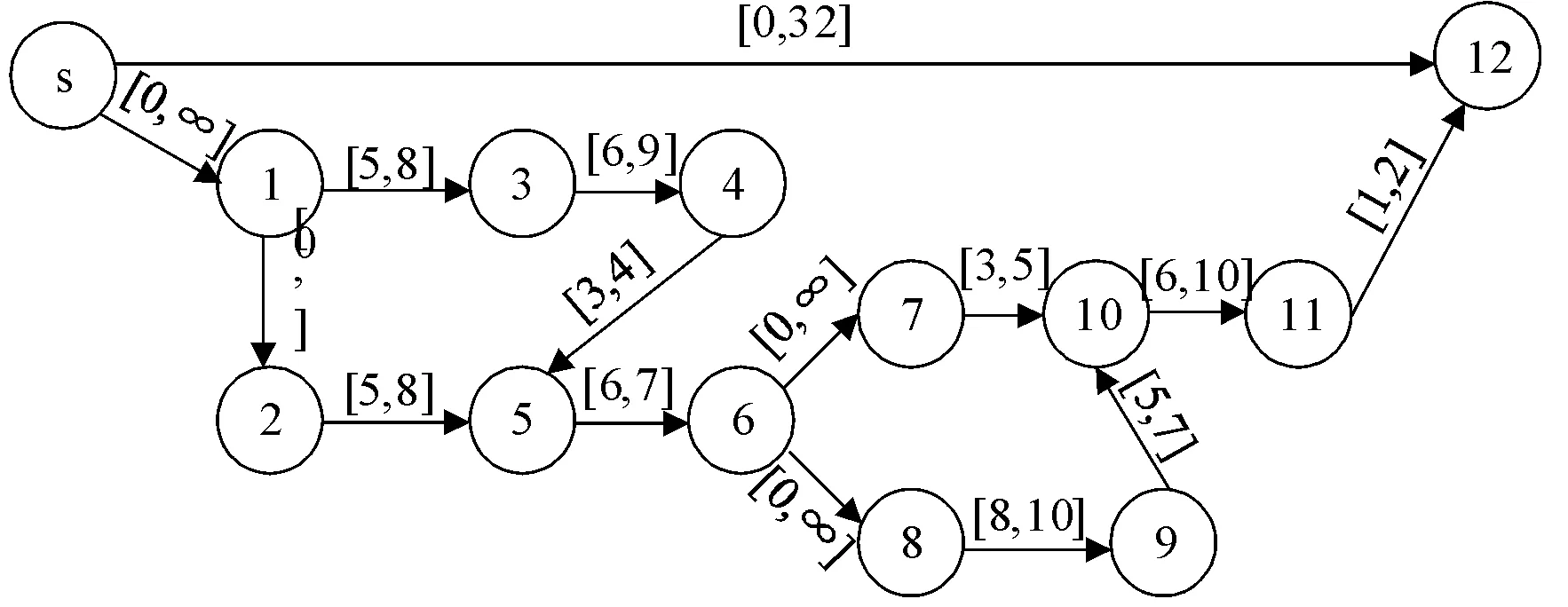
圖8 訓練任務STN圖

訓練任務STN距離圖如圖9所示，用SPFA改進算法對圖8進行一致性檢測，檢測發現該網絡圖存在負環(見圖9中紅色虛線部分)。該任務完成時間為33 min與任務計劃在32 min內完成矛盾，因此出現負環。

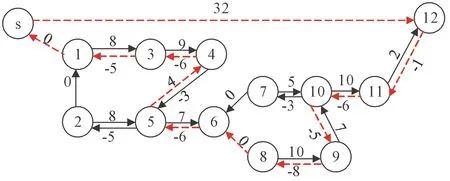
圖9 訓練任務STN距離圖

對案例添加代價系數如表3所示。

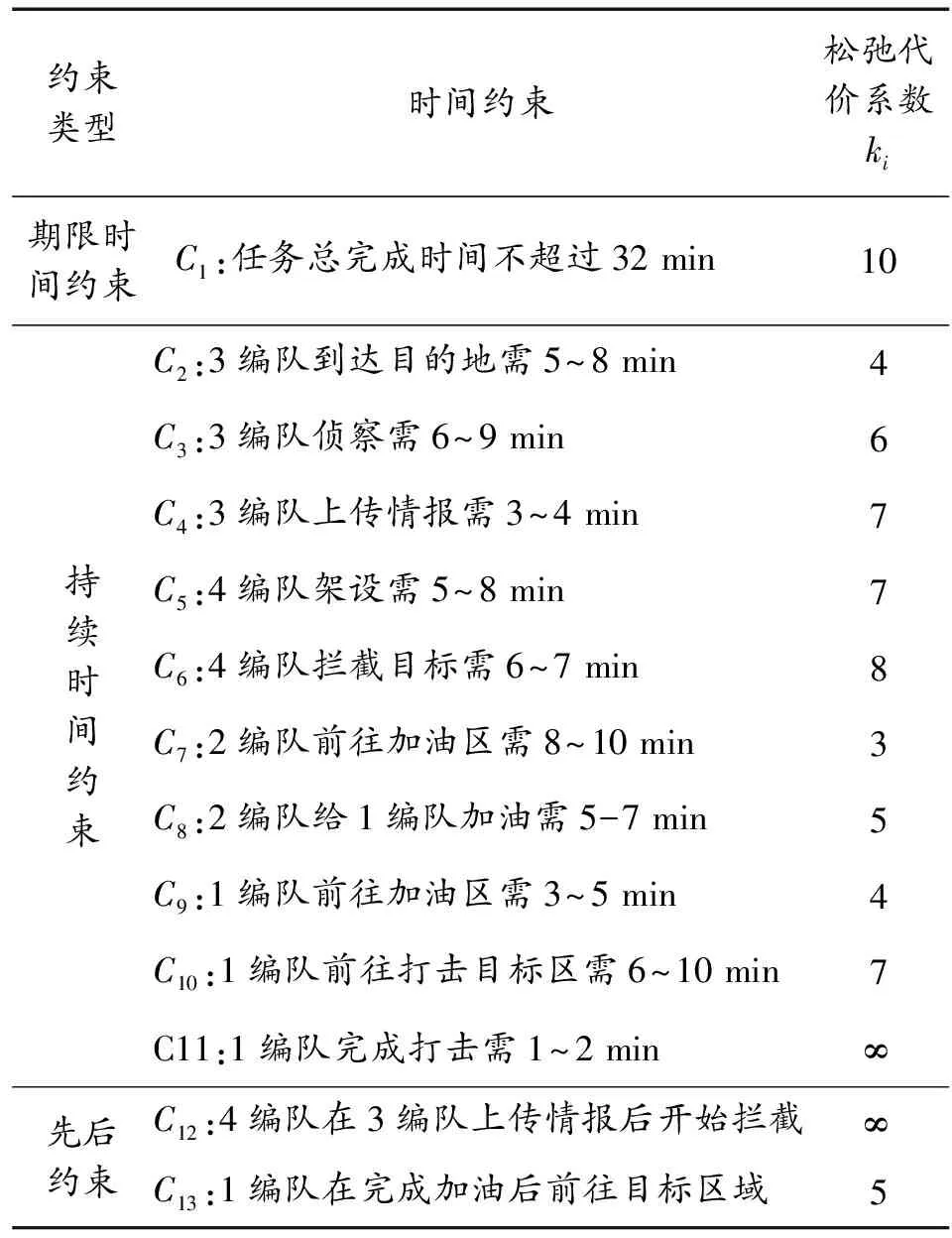
表3 任務時間約束代價系數

對負環消解前列出負環包含的約束，圖9中包含的約束為、、、、、、、、，其中不可調整，其余約束根據式(2)計算出調整代價。約束中代價系數最小的為=3，計算出其調整代價為=3·(1+)，此處=1。

故對進行松弛調整，對其負弧權值加2，此時消解沖突的同時保證調整代價最小。對負環進行消解后其消解沖突結果如圖10所示。

對圖10結果再次進行負環檢測，結果不存在負環，即時間沖突得到消解。

圖10 消解沖突結果示意圖

5 結論

1) 提出基于STN圖的空域預先規劃時間沖突處理方法，對空域預先規劃時間約束進行建模，用STN時間約束網絡圖進行表達，提高了沖突處理的科學性；

2) 提出了基于前驅節點的改進SPFA算法，在負環檢測過程中減少了不必要的循環，提高了計算效率并通過SPFA改進算法對時間約束網絡進行一致性檢測，檢測空域使用計劃是否存在時間沖突；

3) 采用基于最小代價的方法對時間沖突進行消解，并通過對案例的分析證明了方法的可行性。

4) 結合圖論相關內容對空域預先規劃時間沖突處理問題進行研究，提供了一種新的研究思路和方法。后續將針對聯合作戰的特點進行研究。