德伊高鐵地基土變異性分析與概率分布研究
劉先峰,陽 劍,張炎飛,袁勝洋,高澤飛,陳偉志
(1.西南交通大學 土木工程學院,四川 成都 610031;2.西南交通大學 道路與鐵道工程教育部重點實驗室,四川 成都 610031;3.新疆工程學院 土木工程學院,新疆 烏魯木齊 830023;4.中鐵二院工程集團有限責任公司,四川 成都 610031)
土體參數的不確定性一直以來都是阻礙巖土工程發展的重要問題,一般對土體參數的處理辦法是進行數次試驗,以試驗所得結果的平均值作為土體的基本參數。這種做法明顯忽視了土體參數顯著的不確定性,用作工程設計和施工時也隱含不可忽視的風險。因此近幾十年來考慮土體不確定性的理論逐漸發展,針對土體參數不確定性的研究也開始深入。
Phoon等[1-2]將土體不確定性表述為土體變異性,并指出土體變異性主要來自三個方面:①由自然地質過程產生的土體固有變異性;②設備、程序、操作員和隨機測試影響引起的測量誤差;③使用經驗或其他相關模型將現場或實驗室所得數據轉化為所設計土壤性質時引起的轉換不確定性。在巖土工程設計和計算研究領域,學者們也漸漸不再使用確定值來描述土體參數,而是采用隨機分布的形式。Griffiths等[3]在進行隨機有限元分析地基承載力時,采用對數正態分布來表征土體的強度指標c、φ值,取得了較好的計算效果。
現今國內外對于土體各種參數指標的統計分析研究,最基本方法是統計某一土體參數整體的均值、方差(或標準差)以及變異系數[4-5],也有按照數據來源將所研究參數進行分組,按照組別再統計均值與變異系數[1],這樣能獲得較多的均值與變異系數對應點;之后對于土體的概率分布統計特征研究,則通過常規的非參數或者參數方法。
非參數方法主要是頻率分布直方圖法,即采用柱狀圖表示頻數和區間分布,如林魯生等[6]使用頻率分布直方圖對某邊坡抗剪強度參數進行了統計分析,Bilgin等[7]也用頻率分布直方圖統計了土樣的CPT和SPT比值;而常用的參數方法則包括卡方檢驗法以及K-S檢驗方法,如渠時勤等[4]、唐芬等[5]分別對萬州市區、重慶庫區土體進行了卡方檢驗以研究其分布,陳立宏等[8]、張繼周等[9]應用K-S法對土體參數的概率分布類型進行檢驗,而針對巖體參數的研究則有江權等[10]用K-S法檢驗了玄武巖對幾種常見分布的符合情況。
但現今部分研究試驗數據量有所欠缺,對于結果支持度不夠;統計土體指標的方法仍然比較傳統,非參數方法不能獲取土體指標的概率密度函數,而參數方法如卡方檢驗、K-S檢驗效能不高,亟需提高參數方法應用的效能。
因此,本文以我國正在為伊朗建設的德伊高鐵沿線所在地基土的大量實驗室數據為依托,對沿線土體的物理力學參數進行統計分析,研究其變異性及利用概率密度估計方法分析其概率分布特征并進行隨機分布檢驗。分析結果可以作為同種類土體隨機有限元、可靠度分析參數選取依據,也可用作之后重塑土試驗及其性質的對照。
1 土體參數變異性分析
德伊高鐵項目起于伊朗首都德黑蘭,經庫姆,終于伊斯法罕,線路全長約410 km,其中德黑蘭至庫姆新建段約165 km、庫姆至伊斯法罕整治段約245 km。本文分析所用數據來自德伊高鐵沿線地基土的實驗室測試結果,所有測試方法均按照美國材料實驗協會(ASTM)標準進行;數據充分、樣本量大,廣度基本涵蓋整條線路,對其進行分析可以得出較為可信的結果。
德伊高鐵沿線土體以低塑性黏土(CL)、黏土質砂(SC)所占比例最大。CL土為不含有機質的淤泥或黏土,200號篩網(對應孔徑0.075 mm)截留殘余量在50%以下,塑性指數>7,在土壤塑性圖中點落在“A線”之上,其中按照200號篩網截留殘余量以及砂粒和礫粒含量的不同又可分為低塑性黏土、含砂低塑性黏土、含礫低塑性黏土、砂質低塑性黏土、含礫石砂質低塑性黏土、多礫石低塑性黏土、含砂多礫石低塑性黏土共7個更小的種類。SC土屬于砂性土中的一類土,200號篩網截留殘余量在50%以上,但其細顆粒含量超過12%,且細顆粒所處分類為CL或重黏土(CH),較為接近黏性土,其中SC土又可按照礫粒含量分為兩個更小種類,礫粒含量小于15%為黏土質砂,礫粒含量大于或等于15%為含礫黏土質砂。通過篩分試驗得到的現場CL、SC土樣級配曲線見圖1,包括94個CL土樣本和39個SC土樣本。按照各類顆粒含量劃分的CL、SC類土的質地分級三角圖見圖2。
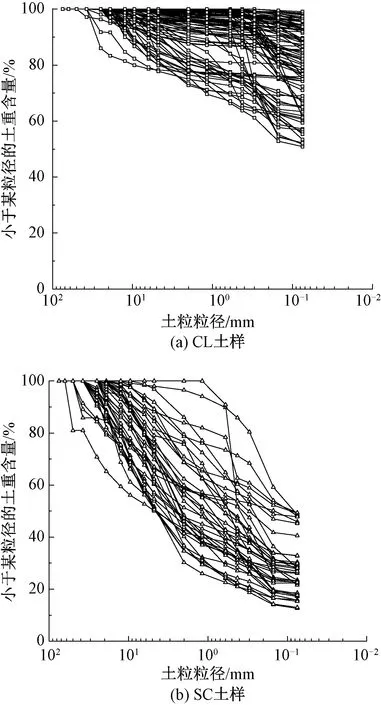
圖1 現場CL、SC土樣級配曲線
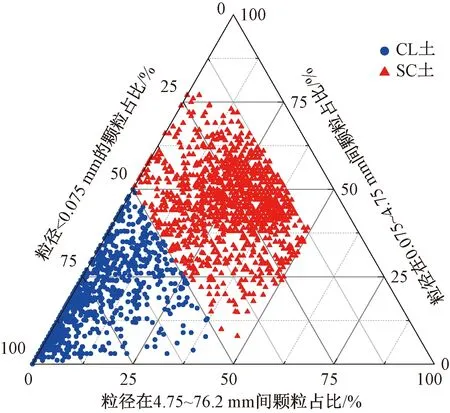
圖2 CL、SC類土的質地分級三角圖
本文主要針對這兩種土體的物理力學參數進行統計分析,包括:天然密度、天然含水率、液塑限、塑性指數以及黏聚力、內摩擦角、壓縮模量。
變異性的評價指標一般用變異系數來描述,即用數據的標準差與均值的比值表示為
(1)
式中:COV為變異系數;SD為樣本標準差;Mean為樣本均值,計算式為
(2)
(3)
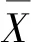
根據Phoon等[1]對土體變異性三大來源的闡述,本文分析的土體變異性將會包含土體固有變異性和測量誤差,因此對上述參數變異性分析的結果將會比土體自身固有變異性偏大。
1.1 實驗室基本物理參數指標變異性統計
本文所研究土體的實驗室基本物理參數指標為天然密度、天然含水率、液塑限以及塑性指數。所有試驗樣本按照試驗所在的里程進行分組,以每2 000 m作為每組數據的分界,即在同一2 000 m里程位置內進行的試驗結果歸為一組,以組為單位進行變異性統計。
本文對CL、SC土天然密度、天然含水率、液塑限試驗結果和塑性指數進行了總結,試驗數據樣本數、組數和均值、變異系數范圍,見表1、表2。

表1 CL、SC土實驗室基本物理參數指標
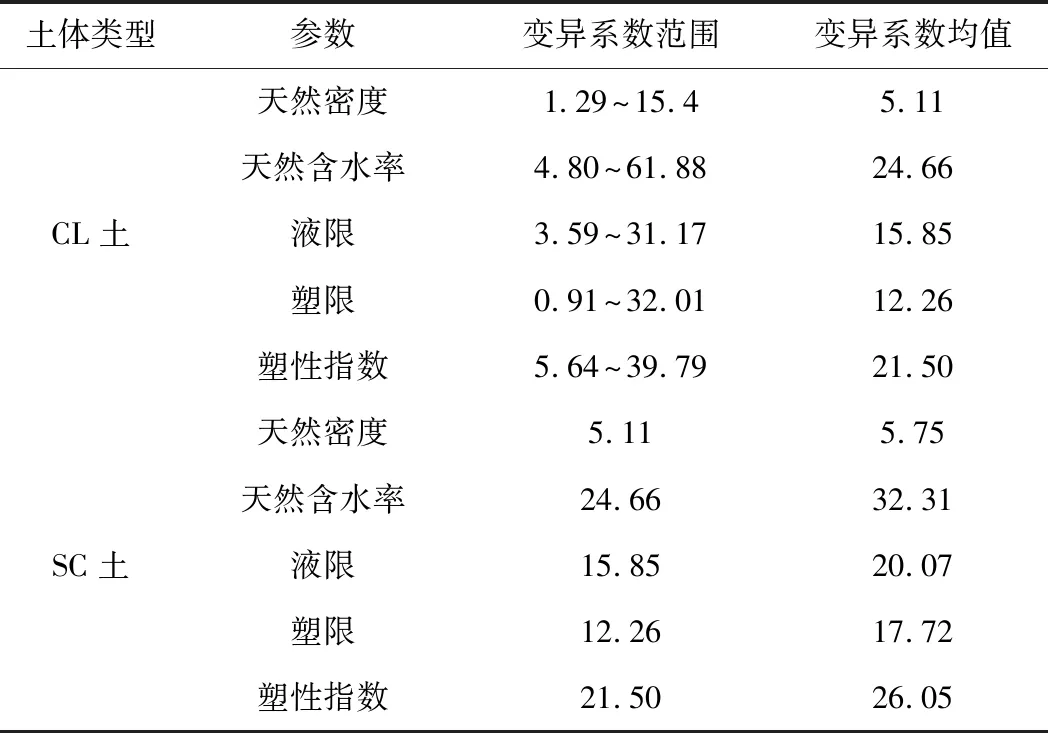
表2 CL、SC土實驗室基本物理參數指標的變異性 %
CL、SC土的液限、塑限、天然密度、天然含水率和塑性指數的均值與變異系數關系見圖3。
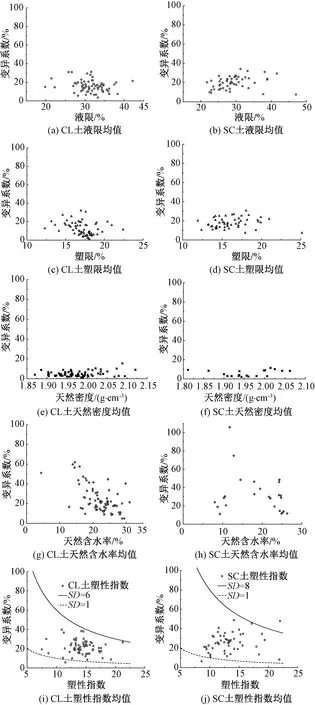
圖3 土體實驗室基本物理參數指標的均值與變異系數關系
由圖3可知,無論何種土體,天然密度的變異性相較于其他參數,始終是最小的,變異系數不超過20%,且一般在10%以下。對于不同的土體樣本,在眾多參數中,密度的變化最小;甚至不同種類土體間,密度的變化也很小。原因為:根據統計的前期固結壓力,整條線路相同土體所承受的前期應力歷史大致相同,進而導致其密度的變異性較小。每種土體的液限和塑限分布圖形比較相似,但液限均值分布范圍比塑限更大,總體上兩種土的液、塑限變異系數均不超過35%。兩種土的塑性指數變異性都比液、塑限更大,但變異系數不超過50%,對CL土使用標準差為1、6的包絡線以及對SC土使用標準差為1、8的包絡線能將絕大多數點涵蓋在內,因此這兩種土的塑性指數在均值附近變化范圍分別為±(1~6)和±(1~8)。天然含水率變異性在兩種土的測試數據中都是最大的,且變異系數分布范圍也很大,但是隨著的天然含水率均值的增大,變異系數有減小的趨勢。這種情況可能與伊朗所處半干旱地區有關:①一般地下土層含水率普遍不高,因此變異性容易受極端值控制而變大;②樣本處于地下水豐富區域時,則含水率會顯著增大,變異性不易受極干、極濕土樣的影響,從而變異系數會變小。
1.2 實驗室強度指標變異性統計
本文研究的土體實驗室強度指標為:土體黏聚力、內摩擦角以及壓縮模量,其中黏聚力和內摩擦角通過直剪試驗中的快剪得到,壓縮模量通過固結試驗得到。
本文對CL土和SC土直剪黏聚力、內摩擦角以及垂直固結壓縮模量試驗結果進行了總結,試驗數據樣本數、組數和均值、變異系數范圍見表3、表4。
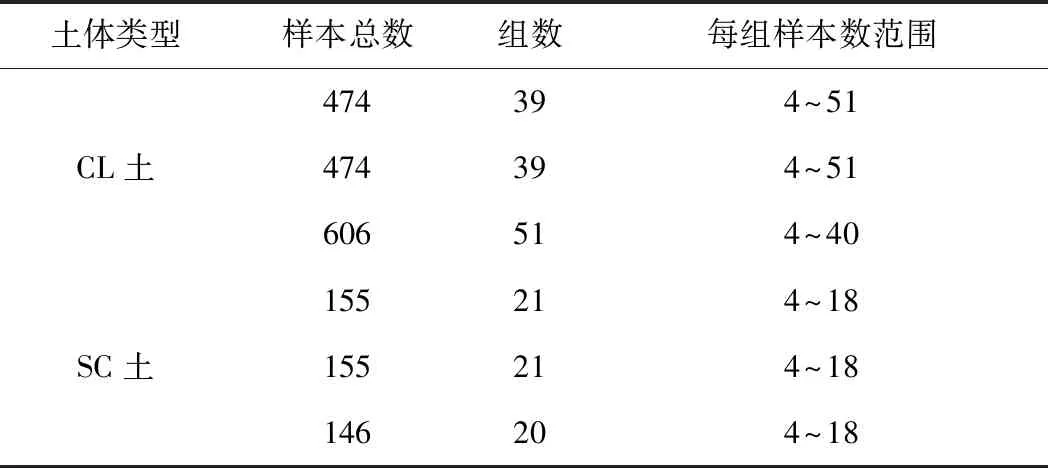
表3 CL、SC土實驗室強度指標
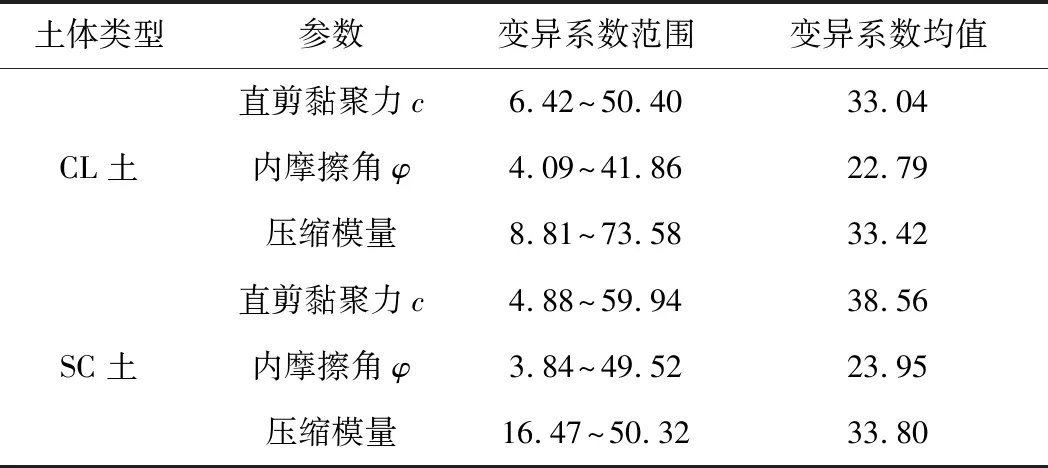
表4 CL、SC土實驗室強度指標的變異性 %
CL、SC土的直剪黏聚力、內摩擦角和垂直固結壓縮模量均值與變異系數關系見圖4。由圖4可知,CL土和SC土強度指標的變異性都比較大,均值和變異系數也在較大的范圍內分布,且沒有明顯規律可循。兩種土強度指標中,內摩擦角的變異性相對其他兩個強度指標更小;除內摩擦角外,直剪黏聚力和壓縮模量的變異系數均值比實驗室基本物理參數指標變異系數均值都更大。
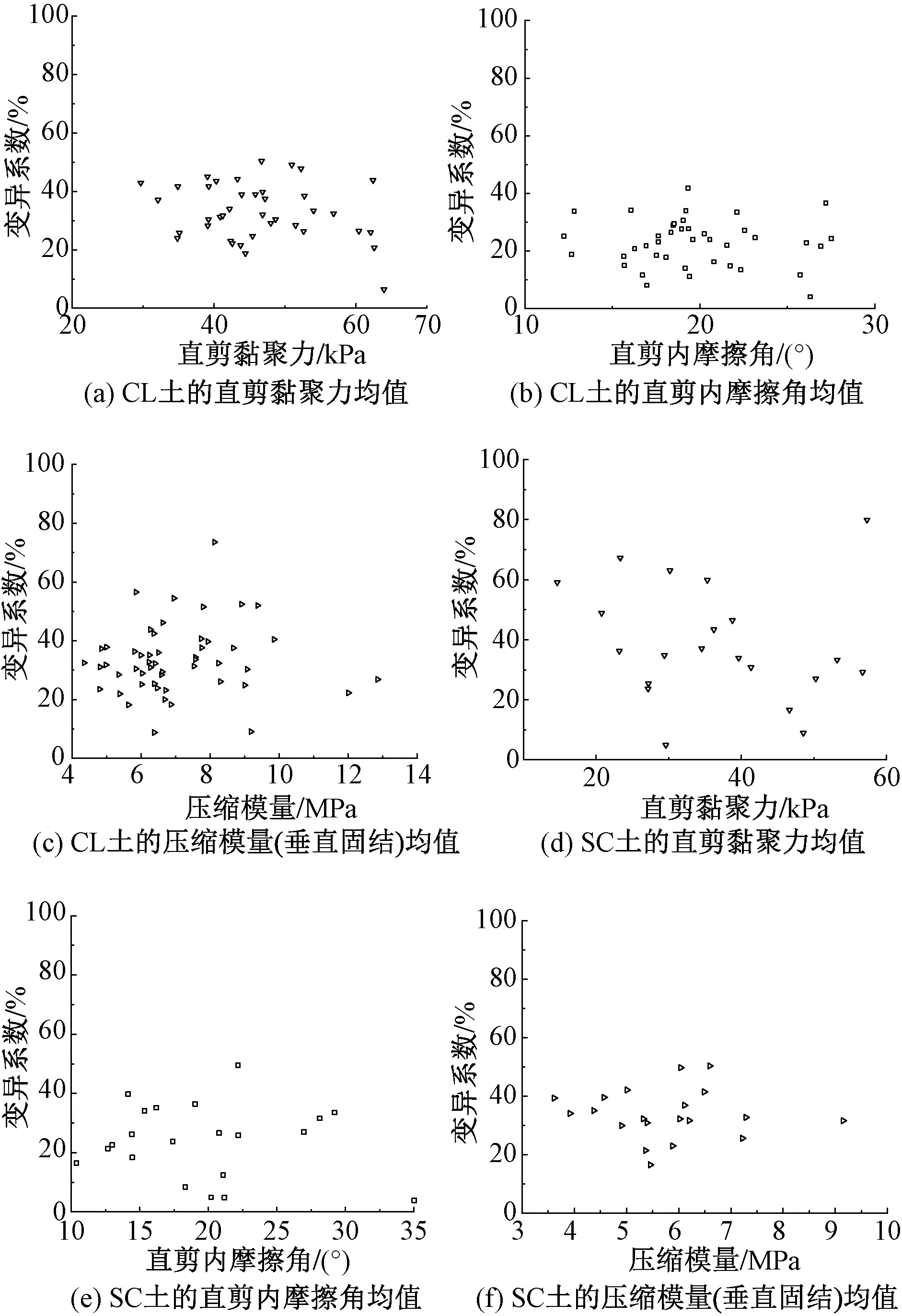
圖4 土體實驗室強度指標的均值與變異系數關系
試驗所得強度指標部分數據結果的均值較為接近,但CL、SC土二者有顯著差別,具體體現在以下兩個方面:①液、塑限以及塑性指數。CL土的液限、塑限、塑性指數三個參數的平均值相比SC土都更大;②黏聚力。CL土黏聚力平均值顯然比SC土大。上述指標越大則表示土體黏粒含量越多。但根據ASTM D2487-17規范[11]對CL與SC兩種土體的定義,從粒徑方面按照200號篩網截留殘余量是否達到50%進行劃分,殘余量十分接近、粒徑重合部分可能較多的情況不能忽視;且CL、SC兩種土又可細分為許多種小的類別,涵蓋的范圍較廣,存在交叉的部分。故二者有相似之處,所以導致其粘聚力、內摩擦角、壓縮模量結果較為接近。
通過本文得出的基本物理參數指標和強度指標變異系數均值的綜合比較,可以得出:德伊高鐵沿線地基土中,CL土變異性比SC土更小。
2 土體參數概率密度及分布估計
通過一般的統計手段,已經初步獲取了土體參數的均值和標準差,這是將土體參數應用在考慮了變異性的隨機有限元以及可靠度分析的第一步。為了使隨機有限元計算以及可靠度分析的結果更為準確,僅僅依靠均值和標準差是遠遠不夠的,還需要明確土體參數每個值的分布區間,因此土體參數具體分布情況是不可或缺的。本文所用獲取土體參數具體分布的方式有兩種:①采用非參數方式估計土體指標的具體概率分布,直接用估計所得的概率分布函數表示土體指標的具體分布,而不借助其他隨機分布表示;②假設土體指標服從某種隨機分布形式,利用我們已經獲得的數據對隨機分布假設進行驗證,驗證結果滿足分布,則得到土體指標服從這種隨機分布的結論。
2.1 非參數方法——土體參數核密度估計
核密度估計法(Kernel Density Estimation)最早由Rosenblatt[12]和Parzen[13]提出,又稱為Parzen窗法,由于此法不事先假定特定分布以及具體參數對數據進行分析,而直接根據所給數據樣本估計指標的概率分布,因此屬于非參數方法。相比利用參數方法假定數據參數模型進行評估,核密度估計法的結果更能符合研究對象的實際物理模型[14]。
核密度估計基本原理:
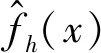
(4)
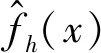
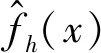
(5)
因此可將核函數選取為常用隨機變量的概率密度函數,常用的核函數有高斯核函數(Gaussian kernel)、Uniform、Triangular、Biweight、Triweight、Epanechnikov等。本文所用核函數為高斯核函數,即正態分布的概率密度函數為
(6)
窗寬h的值對于最后的核密度估計結果也有很大影響,若窗寬h過大,則產生的概率密度估計曲線過分平滑,將忽略掉樣本分布的重要特征;若窗寬h過小,則產生的概率密度估計曲線將會非常曲折陡峭;能將核密度估計函數與真實概率分布函數的誤差降低到最小的窗寬稱為最佳窗寬。Silverman[15]給出了求取高斯核函數最佳窗寬h(即使平均積分平方誤差最小化窗寬)的經驗法則,即
(7)
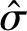
確定了核函數和窗寬之后便可以進行核密度估計,本文采用Python編程實現核密度估計。以CL土液限數據為例,樣本數為799,標準差為0.128,由式(7)計算可得最佳窗寬為0.036。CL土和SC土各參數的最佳窗寬見表5。

表5 CL、SC土各參數的最佳窗寬
CL、SC土各項參數的核密度估計結果見圖5。
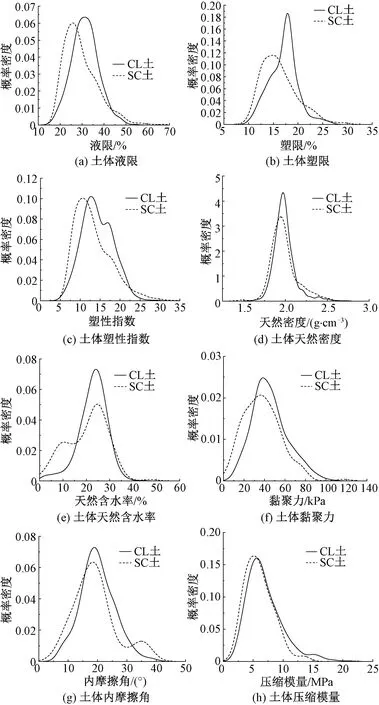
圖5 土體各項參數的核密度估計
由圖5可知,各參數的概率密度分布函數相同點且形狀基本表現為單峰,但是各參數彼此之間存在較大差異;同一種參數中,兩種土的分布圖形也有差異,但天然密度概率分布以及壓縮模量概率分布比較類似。黏聚力、內摩擦角以及壓縮模量呈現單峰以及正偏態分布形式,而在實際的隨機有限元計算中也常將上述參數取為單峰、正偏態的對數正態分布形式,但若要明確上述參數是否符合某種分布,還需要進行分布估計檢驗。
2.2 土體參數分布估計的Anderson-Darling檢驗
Anderson-Darling檢驗由Anderson和Darling[16]提出,用于對樣本分布假設進行擬合優度檢驗。Anderson-Darling檢驗相比傳統檢驗方式如卡方檢驗χ2、KS(Kolmogrov-Smirnov)檢驗,檢驗效能更高[17],能夠克服樣本數量較少以及分布參數為未知等條件下傳統檢驗方式不能檢驗的缺點。Anderson-Darling檢驗的基本原理為:通過比較樣本的經驗分布函數Fn(x)和所假設分布的分布函數F(x)之間的檢驗統計量與檢驗臨界值的大小關系,在顯著度水平α下,接受或者拒絕原假設H0,即判斷樣本是否滿足特定分布。
Anderson-Darling檢驗統計量的具體計算步驟為
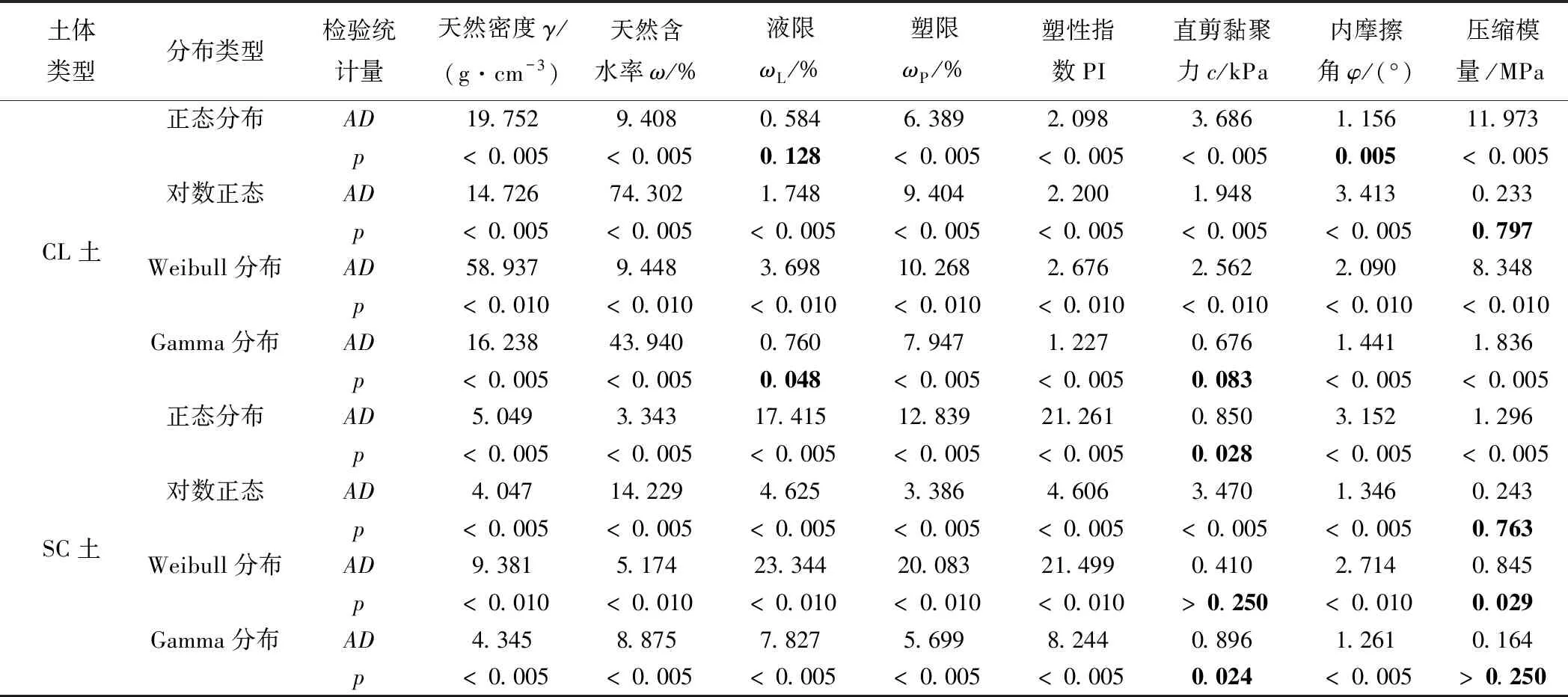
Step1已知n個樣本數據在排序后x1 (8) Step2Fn(x)和F(x)之間的檢驗統計量AD為 (9) 實際應用中常使用離散形式計算檢驗統計量AD,即 (10) 經過證明,在原假設H0為真,假設分布函數F(x)為已知時,檢驗統計量AD與F(x)獨立[18]。 2.1節的核密度估計得到了土體參數的概率密度分布函數,為了全面地分析確定本文所研究的兩種土體各項參數的概率統計特征,采用Anderson-Darling方法,檢驗土體參數是否符合四種常見基本分布,即正態分布、對數正態分布、Gamma分布以及Weibull分布。 正態分布(也稱為高斯分布)是最常見也是最多使用的統計分布。正態分布的概率密度函數為 (11) 如果ln(x-λ)具有正態分布,則變量x具有對數正態分布,其概率密度函數為 x>λσ>0 (12) Gamma分布通常用于模擬具有正向偏斜的數據的分布,其概率密度函數為 x>θa>0b>0 (13) Weibull分布的概率密度函數為 x≥λα>0β>0 (14) 式中:對于正態分布和對數正態分布概率密度函數,σ為標準差;μ為均值;λ為閾值參數。對于Gamma分布,a為形狀參數,控制概率密度曲線形狀,當a=1時與指數分布形狀相同;b為尺度參數,可以縮小和放大坐標尺度;θ為閾值參數;Г為Gamma函數。對于Weibull分布,β為形狀參數,當β=1時與指數分布形狀相同;α為Weibull分布尺度參數。 CL、SC土各自8個參數對于上述4種基本分布:正態分布、對數正態分布、Gamma分布以及Weibull分布的Anderson-Darling檢驗結果分別見表6,進一步將檢驗統計量AD換算成p值,在顯著度水平α=0.05條件下,若p<0.05,則拒絕所給分布假設,反之則認為參數符合給定分布。所有數據來源均為樣本總體,樣本總數見表1~表4。 表6 CL、SC土參數幾種分布假設的Anderson-Darling檢驗 CL土的天然密度、天然含水率、塑限、塑性指數和直剪試驗內摩擦角均不符合所給四種分布假設,而液限檢驗統計量AD=0.584,p>0.05,符合正態分布。同理,直剪黏聚力符合Gamma分布,壓縮模量符合對數正態分布。而SC土的天然密度、天然含水率、液限、塑限、塑性指數和內摩擦角均不符合所給四種分布假設,而其直剪試驗黏聚力符合Weibull分布。壓縮模量既符合對數正態分布同時也符合Gamma分布。除黏聚力和壓縮模量外,其余參數基本不能符合四種基本分布形式。出現這種結果可能的原因為:所有數據樣本均沒有考慮深度的影響,即樣本來自所有深度,沒有按照深度進行劃分,而深度對于各項參數的影響是比較顯著的;但通過固結試驗獲得的壓縮模量對深度變化不敏感,所以比較能符合特定分布,如對數正態分布。 通過進一步研究可以發現,本文未使用的某些多參數分布假設對于所用樣本的擬合優度可能更好,如三參數對數正態分布、三參數Weibull分布以及三參數Gamma分布,但是由于其復雜性,應用成本也較高。 (1)根據德伊高鐵沿線所在地基土的實驗室數據,統計了沿線兩種主要CL、SC土的物理力學參數并分析其固有變異性:總體來看,實驗室基本物理參數指標變異性相比除內摩擦角以外的強度指標變異性更小,其中天然密度變異性最小;若根據土的種類來分,則各項參數中CL土相比SC土的變異性都更小。 (2)利用核密度估計法對于所有樣本對應的概率分布進行了估計,結果顯示所有土體參數核密度統計情況基本符合單峰分布,但各項土體參數的核密度結果之間存在較大差異。本文還使用Anderson-Darling檢驗方法,對德伊高鐵兩種主要土體的各項參數是否符合特定分布進行了檢驗,發現大部分參數并不符合所給4種隨機分布模型(正態、對數正態、Weibull、Gamma),其中實驗室基本物理參數指標符合特定分布的最少,相反三個強度指標黏聚力、內摩擦角、壓縮模量符合特定分布最多。利用核密度估計所得分布相比Anderson-Darling檢驗使用特定分布對樣本進行擬合,更能符合實際情況,得到概率密度函數、體現具體分布的細節,使計算結果更準確,但是應用起來也稍為復雜。 土體變異性是其固有屬性,且相比其他材料變異性更大,研究其變異性和分布形式是在巖土工程中開展隨機有限元、可靠度分析的基礎,本文分析結果可以作為德伊高鐵項目中隨機有限元、可靠度分析的土體參數選取依據,也可用作之后重塑土試驗及其性質的對照。進一步的研究將需要來自更廣泛地區以及數量更多的樣本數據。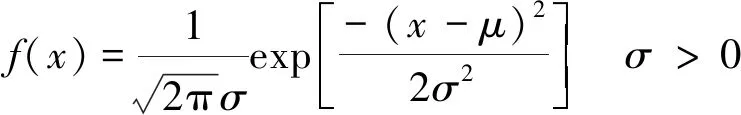
3 結論

