高速鐵路定期票產品定價優化研究
苗 蕾,王 煜
(1.北京交通大學 交通運輸學院,北京 100044;2.中國鐵道科學研究院集團有限公司 電子計算技術研究所,北京 100081)
2020年起,鐵路運輸企業推出計次票、定期票等新產品,廣受市場歡迎,尤其是定期票產品。定期票產品以“公交化、便利化出行”為設計理念,主要針對通勤旅客和部分商務旅客,通過“量多價惠”的原則吸引目標旅客,增加用戶黏性,提高市場占有率。定期票持有者可在規定時間內乘坐規定次數,購買產品時指定發到站及席別的列車。旅客可按出行期限靈活選擇產品,如5、10、30日定期票等。定期票產品推出時間較短,無直接“量化的定價理論”可供參考,價格制定還處在探索研究階段,目前鐵路定期票產品定價主要依靠各級價格管理人員的經驗,缺乏量化的理論模型來確定定期票產品的合理價格,難以最大化鐵路運輸企業收益。
定期票在城市公共交通等領域已有應用,如公交、城市軌道交通等,多以周末票、7日票、月票等形式推出。但鐵路定期票產品應用場景與上述公共交通票務產品區別很大,能夠從中借鑒的極為有限,高速鐵路(以下簡稱“高鐵”)定期票產品定價是一項嶄新的命題。另一方面,既有關于定期票產品定價理論研究較少,尤其是帶有數據和模型支撐的量化理論研究幾乎為空白,難以借鑒既有研究成果。
定期票定價屬于鐵路客運產品定價范疇,與鐵路主流定價理論具有共通性。文獻[1]研究交通運輸產品即易逝品的定價問題。文獻[2]研究不確定需求下單一產品定價模型。文獻[3]構建基于多列車多停站的票額和票價綜合優化模型,根據模型特點設計混合啟發式算法,從而得到不同列車在不同區段的不同定價,解決差異化定價的問題。文獻[4-5] 研究我國鐵路實施客票折扣銷售的可行性及相關折扣制定依據。文獻[6]以時間敏感性、價格敏感性及出發時段偏好為基礎,對旅客進行分類,再研究同一區段兩列平行列車的動態定價問題。文獻[7-8]首先模擬旅客需求函數,得到客運產品需求與票價的數學關系,再逐步構建高鐵動態票價優化模型并求解。文獻[9]以京滬高鐵為例,考慮多種交通競爭方式,基于Logit模型構建票價與收入的關系范式,得到收益優化后的票價范圍。文獻[10]構建不同時刻、不同運輸方式的旅客出行廣義費用函數,建立雙層規劃模型,優化不同時段城際鐵路票價。文獻[11]依據最大凹向包絡理論,建立基于乘客出行選擇行為的動態定價策略模型。本文基于以上理論模型,研究單列車多停站定期票定價優化模型。
1 參數定義與假設
為研究定期票定價問題,對部分內容進行簡化和假設:
①不考慮退票、改簽對定價過程的影響。
②定期票定價基準對象是始發終到區間。
③每位旅客都是理性人,以自身利益最大化為出發點決策是否購買定期票,非始發終到旅客一般不會購買定期票,除非可以套利。購買定期票后旅客不會乘坐非始發終到的短區間。
④以二等座為研究對象。
主要變量及其含義見表1。

表1 主要變量及定義
2 模型構建
2.1 旅客需求分析
旅客根據其乘車歷史判斷是否購買定期票,對于某列車始發終到區間來說,旅客決定購買定期票的原因:①自身歷史參考期(某個時間段)內實際乘車花費高于定期票價格,購買定期票產品劃算;②更加便捷(隨時預約席位,預約最多10個席位,不用每次提前購票,提高乘車效率),部分旅客考慮定期票出行的便捷性,同時考慮到自身在歷史參考期的花費僅略低于定期票價格,決定以提高少量花費換取乘車便捷性從而購買定期票產品;③部分旅客雖然在歷史參考期實際花費低于定期票價格,但定期票單次乘車價格下降會使這部分旅客預期增加乘車次數,從而購買定期票。對于情況②和③,旅客在歷史參考期的實際花費比較接近定期票產品價格才有可能最終選擇購買定期票產品。本文引入預期系數概念β對情況②和③的旅客在歷史參考期的實際花費接近定期票產品價格的程度進行度量,再結合情況①得到定期票旅客判別條件Φ為
(1)
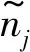
(2)
(3)

(4)
(5)
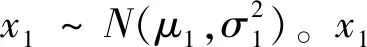
(6)
(7)
(8)
式中:μ1、σ1分別為該正態分布的均值、標準差。
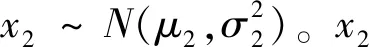
(9)
(10)
(11)
式中:μ2、σ2分別為該正態分布的均值、標準值。
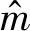

(12)
式(12)表示定期票旅客在購買定期票后相對于歷史參考期乘車次數會調高自己在時間段t內的實際乘車次數。時間段t內,如果(r,s)為非始發終到區間,則(r,s)只有非定期票旅客乘車需求,其客流需求假設服從獨立的正態分布,則其客流需求概率密度函數為
(13)
式中:μrs、σrs分別為該正態分布的期望和標準差。
區間(r,s)期望售出數量Qrs為
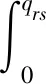
(14)
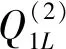
(15)
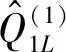
(16)
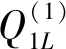
(17)
時間段t內總定員Ct為
Ct=t·C
(18)
式中:C為列車定員。
同時以上分析需要滿足約束
(19)
(20)
(21)
qrs∈N 1≤r (22) 式(18)~式(20)為列車能力約束,式(21)為定價約束,式(22)為整數約束。 對于鐵路運輸企業,在時間段t,始發終到區間定期票產品提供的收益R1為 (23) (24) 非始發終到區間收益R2為 (25) 最終單列車多停站下的定期票定價優化模型為 (26) s.t. 式(18)~式(22) 模型是帶約束條件的隨機非線性規劃模型,需要選擇啟發式算法求解。粒子群算法具有迭代過程簡單、易于理解、依賴參數少等優勢,可兼顧求解復雜度和效率,采用粒子群算法對模型求解。 式(26)需要同時優化定期票票價和票額兩個變量,為簡化后續求解,降低解向量的維度,先將所有非定期票旅客的收益計算公式合理轉化為等效模型[13]為 (27) s.t. 式(20)、式(22) q1L≥μ2 (28) (28) 式中:gh為與A維度相同的向量,各分量服從(-d,d)上的均勻分布,d為整數。 (29) (30) (31) (32) h=1,2,…,Psize (33) 圖1 求解過程 由于目前定期票推出的時間還太短,還多旅客還不了解定期票產品,真實銷售數據還不能反映真實的需求;同時為簡化問題復雜度,提高模型迭代效率,基于本文假設的統計學分布生成模擬數據對單列車多停站下的定期票定價優化模型進行算例分析。假設定期票設定乘車有效期為10 d,t=10。允許最大乘車次數為10次,m=10。定期票乘車區間為北京南至上海虹橋,涉及唯一列車為G22。G22定員1 103,C=1 103。經停南京南站,共涉及3個區間:北京南至上海虹橋,北京南至南京南,南京南至上海虹橋。取J=2,北京南至上海虹橋區間旅客乘車次數分布見表2、表3。 表2 第1個標本時間段旅客乘車次數分布 表3 第2個樣本時間段旅客乘車次數分布 北京南至南京南、南京南至上海虹橋發送量均值和標準差數據見表4。 表4 非始發終到區間客流量 人次 各區間票價見表5。 表5 各區間票價 根據鐵路客運一線價格管理人員的專家經驗估算預期系數β=1.5,激勵系數α=1.2。定期票價格上限為正常乘車總價格即6 310元,為了防止非始發終到區間旅客通過購買始發終到區間定期票套利,也為了打消購買定期票旅客乘坐非始發終到短區間的可能性,需要分析定期票最低限價,非始發終到區間中最高票價區間為北京南至上海虹橋,票價為504元,因而定期票下限(乘坐10次)為5 040元。 利用Python實現求解過程,設定粒子規模Psize=20,最大迭代次數為300次,收斂控制系數δ=1,φ1=0.5,φ2=0.5。以正常乘坐9次價格5 679元和定期票潛在旅客數量樣本均值82作為初始解輸入模型求解。迭代過程見圖2,可知在迭代到40次左右時達到收斂,最終定期票價格5 678元,取得總收入366.8萬元。各區間票額分配結果見表6。 圖2 算法迭代過程 表6 各區間票額分配結果 從表6可知,以10 d為定期票使用期限,需單日分配給北京南—上海虹橋定期票旅客席位126個。對于非定期票旅客,北京南—上海虹橋分配票額3 917張,北京南—南京南分配票額6 445張,南京南—上海虹橋分配票額6 445張。最終。以不推出定期票所有區間票額正常售出為對比方案,在t1和t2兩個樣本期平均收入為360萬元,可知本文推出的定期票產品5 678(10,10)可以幫助鐵路運輸企業提高收入1.9%。 本文以解決客運價格管理實踐中的實際問題入手,提出一種針對定期票產品定價的優化模型。首先假設旅客需求呈現正態分布,其次引入預期系數與激勵系數模擬旅客決策行為從而得到定期產品的潛在旅客需求函數,最后以收益最大化為目標構建基于單列車多停站的定期票定價優化模型并求解。該模型將現有鐵路定價理論與實際應用場景相結合,保證一定程度的落地應用,為各級價格管理人員提供了一種定期票定價決策方法,彌補了目前定期票產品定價過程中過于依靠人工經驗的瑕疵。算例模擬結果表明通過本文提出的定期票定價模型能夠提高總體收益1.9%,保證鐵路運輸企業繼續擴大推廣定期票產品的積極性,同時也為通勤旅客帶來更適合的運輸產品,增強鐵路市場競爭力,實現鐵路運輸企業與旅客的雙贏。 但是,本文是以單列車多停站下的應用場景,與多列車多停站的實際應用場景還有差距。同時,本文的假設也與實際條件有一定差距,尤其是旅客會在購買定期票后在短區間乘車這一現象會使得本文研究問題更加復雜,這些都是下一步需要深化研究的。2.2 定期票定價優化模型
3 模型求解
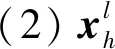
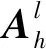
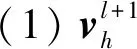
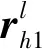

4 算例模擬
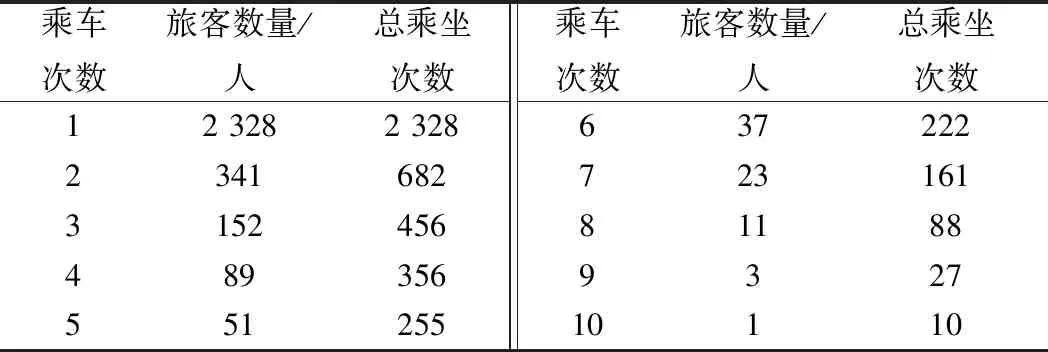
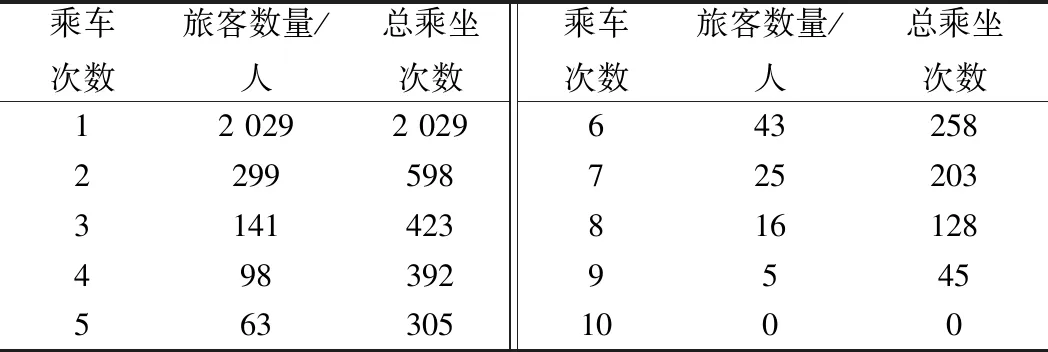
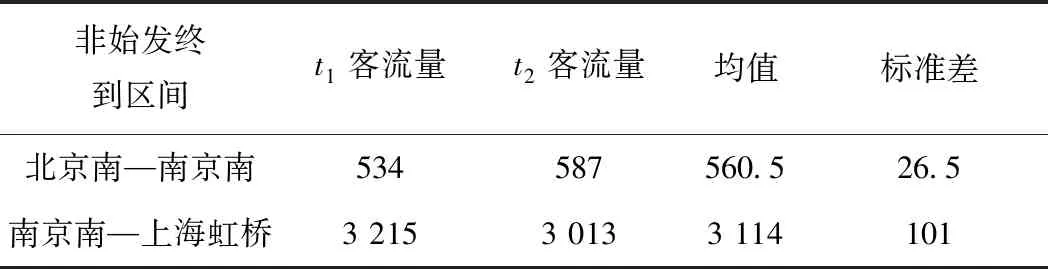

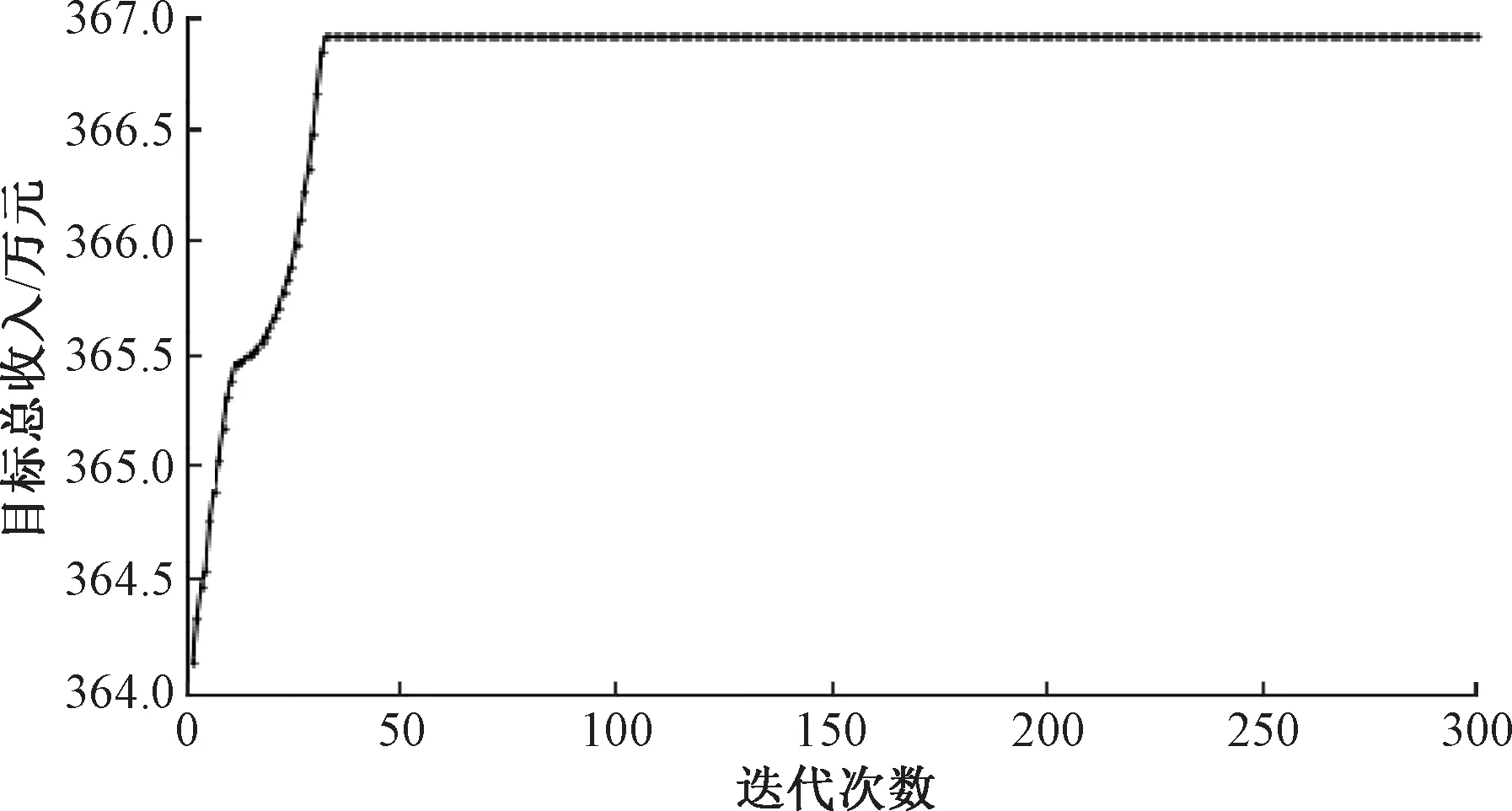

5 結論

