列控車載設備現場測試案例執行距離估算方法研究

張亞東，袁榆淞，饒 暢，郭 進

(1.西南交通大學 信息科學與技術學院，四川 成都 611756；2.重慶交通大學 交通運輸學院,重慶 400074)

CTCS-2級列控系統是基于軌道電路和點式信息設備傳輸行車許可的列車運行控制系統，由地面設備和車載設備組成，其中車載設備是對列車速度進行防護的重要設備。為保障行車安全，車載設備在投入運營前必須進行一系列嚴格的測試。按照測試階段的不同，可分為實驗室仿真測試、現場測試、互聯互通測試和聯調聯試等[1]。

車載設備的現場測試通常是一個動態、連續的過程，對應的測試案例數量龐大。為了縮短測試周期，提高測試效率，通常會將若干個測試案例按照一定原則有序串接形成測試序列連續執行。近年來，國內外研究人員圍繞測試序列的合理高效串接問題進行了大量研究。張勇等[2]基于圖論方法，以車載設備運行模式為框架，采用中國郵路問題的求解思路尋求測試序列的優化串接方法。趙曉宇等[3]針對測試序列串接過程中的算法搜索死循環和狀態空間爆炸問題，提出了一種基于有色Petri網的測試序列生成方法。ZHENG等[4]為降低測試序列對于測試案例的重復覆蓋程度，提出了一種基于全路徑覆蓋的測試序列優化選擇算法。

上述研究主要解決實驗室仿真測試階段的測試序列串接問題。與實驗室仿真測試不同，在現場測試階段，串接測試序列還需進一步考慮實際線路條件約束，從而確保測試案例在符合條件的線路區段得以執行。合理估計測試案例的執行距離，是串接現場測試序列的關鍵之一。現有估計測試案例執行距離的相關研究主要依賴于人工經驗，將現場測試案例的執行距離粗略劃定為某個固定長度。袁磊等[5]選定線路上相鄰間距大于500 m的應答器組位置作為測試案例的布置點，從而將相鄰布置點的距離估計為測試案例的執行距離。李彬[6]將線路上長度大于200 m的計軸區段劃定為測試區段用于布置測試案例，從而把測試區段的長度估計為測試案例的執行距離。類似的還有李智[7]等提出的方法等。然而，現場測試案例的執行距離受執行步驟數量、操作類型、線路條件、列車運行模式、動力學狀態等多種因素影響，往往會發生動態變化。現有方法未能充分考慮這些因素，因而容易出現執行距離長度劃分不合理的情況，導致列車在測試過程中發生空跑，甚至無法在規定區段內執行完測試案例，進而造成測試中斷、測試過程能耗大、成本高等問題。

針對上述問題，本文提出一種基于列車動力學模型的現場測試案例執行距離估算方法，通過建模描述列車在現場測試過程中的動力學狀態變化情況，采用列車動力學分析方法，綜合考慮線路條件、司機反應時間、操作類型等因素影響，計算列車在各動力學狀態下的運行速度、位置變化規律，近似估計列車執行該測試案例的走行距離。然后基于實驗室測試平臺對案例進行測試執行驗證，以對本文提出的方法進行檢驗。

1 車載設備現場測試過程

車載設備的現場測試通常以相關技術規范為依據[8]，通過安排列車在現場實際線路上運行，對車載設備應答器信息接收、動態曲線計算、速度監控、最限制速度曲線計算等功能特性進行測試，覆蓋站內接發車、區間追蹤、自動過分相、模式轉換等運營場景。現場測試案例可由專家經驗[9]或軟件測試理論方法[10]構造得到，通常具備一定的執行距離，測試人員通過人機界面(DMI)、記錄單元(JRU)等接口觀察測試過程中車載設備的狀態變化和預期輸出。

測試案例1：“在完全監控模式下，列車接收到【CTCS-5】絕對停車信息包，應觸發緊急制動直至停車”。

如圖1所示，測試案例1開始執行時，列車以速度vA處于A點，DMI圖標顯示當前模式為“完全”；列車保持勻速前行，到達B點，此時列車速度vB=vA，車載設備接收并解析地面應答器發送的【CTCS-5】絕對停車信息，DMI速度指針及環形光帶顯示為紅色，并驗證輸出緊急制動；列車在緊急制動狀態下降速運行，直至在C點處停車，此時列車速度vC=0；DMI給出允許緩解語音提示后，測試人員按壓緩解按鈕，緩解制動，至此測試案例1執行結束，列車運行至下一條測試案例的執行范圍內。

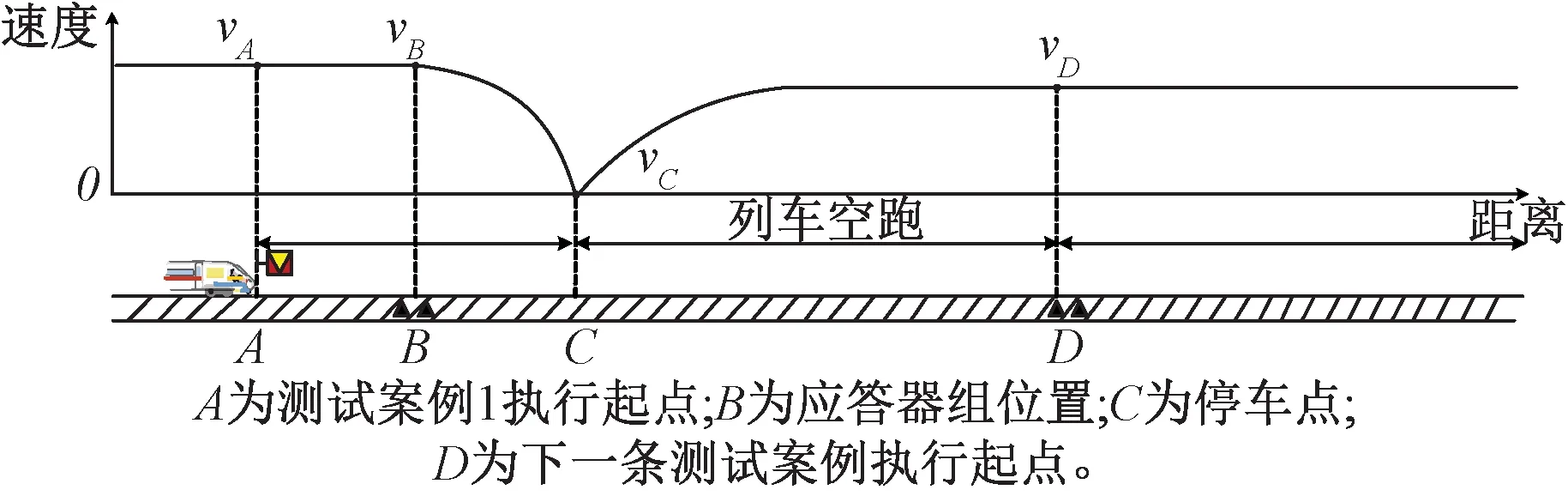
圖1 現場測試過程舉例1

由圖1可見，該測試案例的實際執行距離為AC段。然而，如果對測試案例的預估執行距離出現較大偏差，比如執行距離被預估為AD段，則會造成列車在CD段的空跑，由此將帶來測試成本升高、測試效率降低等問題。反之，若實際執行距離大于了預估的執行距離，且測試序列串接時對案例執行距離的誤差余量選取不合理，則可能造成當前測試案例的執行范圍侵占到下一條測試案例的執行范圍，直接導致下一條測試案例無法在規定的線路條件下執行，進而導致現場測試序列發生中斷。因此，合理估計測試案例的實際執行距離，不僅有助于縮短測試過程中列車的空跑距離，而且可以避免發生測試中斷，從而有利于高效合理地串接現場測試序列，降低現場測試能耗和成本，提高測試效率。

2 測試過程狀態模型

測試案例的執行距離與案例的執行步驟數量、操作類型、線路條件等密切相關，且不同測試案例的執行步驟往往具有較大的差異，這給直接計算測試案例的執行距離帶來了巨大困難。然而，本文注意到列車的動力學狀態變化是貫穿整個測試執行過程最顯著的特征，也是影響測試案例執行距離的關鍵內在因素。因此，本文從該特征入手，提出以列車動力學狀態作為紐帶，對不同測試案例的執行過程進行統一、抽象化的描述，從而為估算測試案例的執行距離提供依據。

2.1 模型構建

由于列車執行現場測試案例是一個連續且動態的運行過程，因此本文把列車在執行測試案例過程中所有可能出現的動力學狀態抽象為點的集合，狀態之間的變化關系抽象為邊的集合，從而構建出車載設備測試過程的有向圖模型G=(S,E)。其中，S為列車運行狀態的頂點集合，S={S0,S1,S2,S3,S4,S5,S6,S7}；E為列車運行狀態變化關系的有向弧集合，E={e1,e2,…,e31}；測試案例的執行過程則是有向圖模型G中頂點S0到頂點S7的某一條路徑。車載設備測試案例執行過程的有向圖模型見圖2，圖2中各頂點變量的含義見表1。

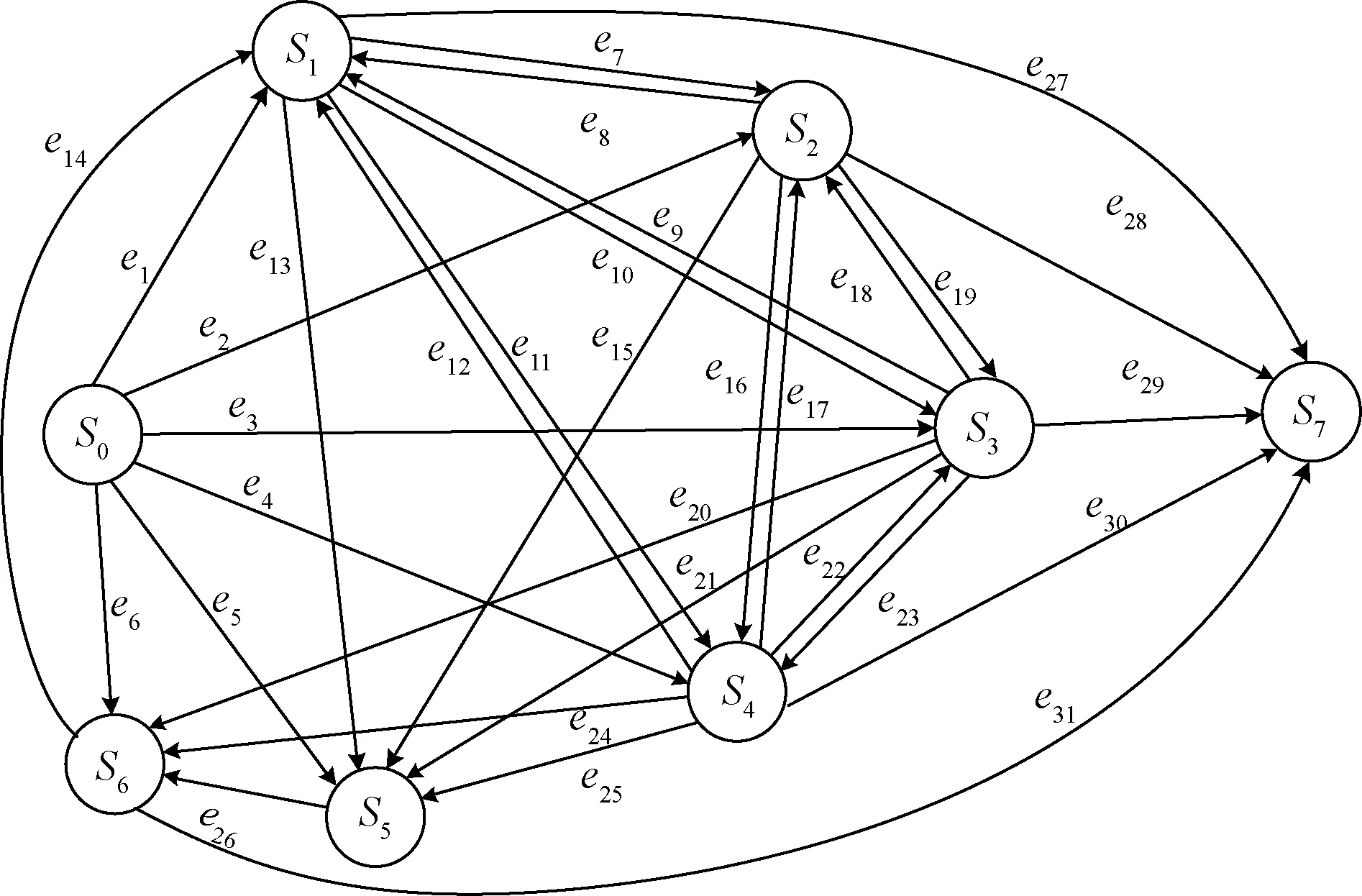
圖2 車載設備測試案例執行過程的有向圖模型

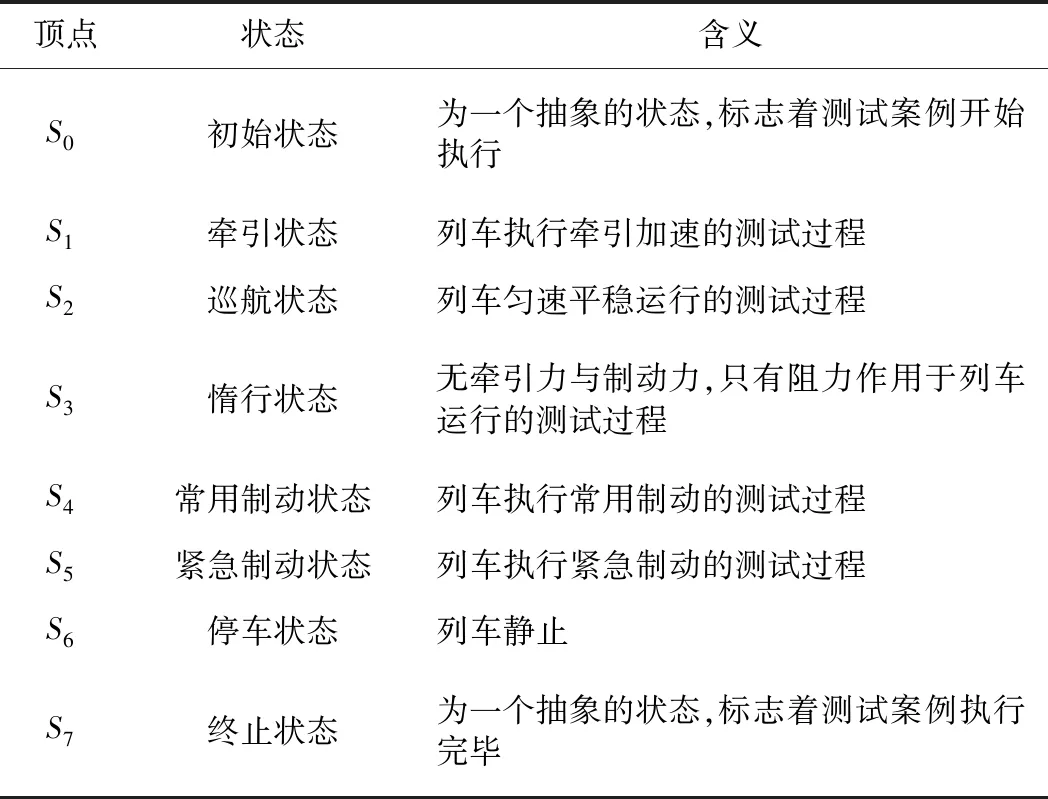
表1 模型中頂點變量的含義

對于測試案例1，根據列車的動力學狀態變化情況，列車分別依次經歷了巡航狀態、緊急制動狀態和停車狀態，其測試執行過程的有向圖路徑可以表示為S0→S2→S5→S6→S7。注意，本文將S0、S7兩個狀態定義為標志測試案例開始執行和執行結束的抽象狀態，對應的走行距離規定為0。此外，執行測試案例的不同步驟可能造成列車動力學狀態反復發生多次變化，因此路徑中的頂點可能會重復出現。例如在某次測試中，列車分別依次經歷了巡航狀態、緊急制動狀態、停車狀態、牽引狀態、巡航狀態和牽引狀態，其有向圖路徑表示為S0→S2→S5→S6→S1→S2→S1→S7，此時頂點S1、S2各重復出現2次。

測試過程模型刻畫的是不同測試案例執行過程中的列車動力學狀態宏觀演變情況，而測試案例之間的微觀差異，如執行步驟與數量、操作類型、所需線路條件等，將在后續計算案例的執行距離時做進一步考慮。

2.2 相關定義

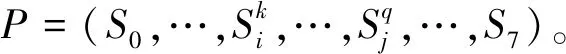
規定列車在兩個相鄰動力學狀態變化中，后一狀態的入口速度等于前一狀態的出口速度。

在測試案例的某些執行步驟中，通常會明確地或隱含地給出列車運行的部分距離，這些給定的距離將會影響到測試案例的執行距離估算，相關定義和說明如下。

定義4固有距離：測試案例執行步驟中明確給出的運行距離，記作Lg。按照距離的直觀性可分為顯式固有距離和隱式固有距離。

定義5顯式固有距離：測試案例執行步驟中以數值的形式直接給出的距離信息，記作Lgx。例如測試案例步驟中描述了“列車運行50 m后，收到應答器報文”，那么Lgx=50 m。

定義6隱式固有距離：測試案例執行步驟中未以數值形式給出距離長度，但是可以根據涉及到的特殊運營場景，查閱車輛參數或線路數據等確定的運行距離，包括車長、分相區長度、等級轉換中預告點與執行點之間的距離等，記作Lgy。

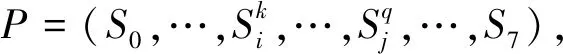
測試案例2：“列車以速度100 km/h運行，200 m后運行至應答器組A處，接收到【ETCS-5】應答器鏈接包，給出下一個被鏈接的應答器組編號為2，列車運行到下一被鏈接的應答器組B，讀取應答器編號為3，與鏈接信息不符，車載執行鏈接反應輸出緊急制動”。

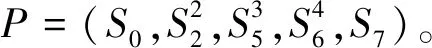
3 測試案例執行距離估算方法

3.1 方法框架

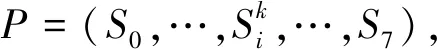
輸入：車輛參數、線路數據、測試執行過程的有向圖路徑P、測試案例執行步驟、固有距離Lg。

輸出：測試案例執行距離L。

開始

初始化L←0

for(intk=2 to ∣P∣-1) 執行

continue

else

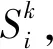
end if

end for

L←L+Lg

returnL

結束

該方法主要包括如下步驟：

Step1獲取車輛參數(包括車長、車重、牽引特性曲線、目標制動減速度等)和測試區段的線路數據(包括線路坡度、曲線半徑、線路限速、特殊區段位置等)，并根據測試執行步驟構建測試執行過程的有向圖路徑P。

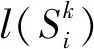
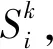
Step4所得結果與固有距離Lg相加，輸出測試案例執行距離。

3.2 距離計算

表2中：a牽n為第n步牽引加速度，m/s2；vn為第n步速度，m/s；dn為第n步的位置，m；Δt為單位時間步長，設置為0.5 s；t2為列車在巡航狀態下的運行時間；L分相區為線路數據提供的分相區長度，m；L斷為列車斷開主閘時距離分相區起點的距離，m；L合為列車駛出分相區后到合上主閘的走行距離，一般取值為130 m；t斷為輸出過分相命令信號時車頭距分相區起點的時間,一般取值為10 s；v觸為列車觸發制動的速度，m/s；t空為列車空走時間，s；v緩為允許緩解速度，m/s；a制n為第n步常用制動加速度，m/s2。

表2 不同狀態下測試執行距離計算方法

對于巡航時間t2，通過分析具體的測試步驟可知，t2主要取決于測試過程中測試人員人工操作設備、觀察或記錄所花費的時間。本文根據現場測試過程的操作步驟及其復雜度依托列控車載設備測試平臺[11]進行了多次模擬試驗，將不同類型的操作步驟及其所花費時間進行了統計分析，見表3。

對于追加的補償距離，在人控優先方式下，觸發常用制動后，從DMI給出允許緩解指示到司機按壓緩解按鈕，再到車載設備取消制動，這一過程存在延時，使得列車在常規制動狀態的出口速度低于規定的允許緩解速度，故需再加上補償距離才能計算得到列車在該狀態的測試執行距離。進行計算時，延時可由表3確定為4.5 s，并以允許緩解速度作為初速度，采用分段迭代法進行制動計算，所得的列車運行距離增量即為補償距離，速度即為出口速度。

表3 測試人員的操作類型及其期望花費時間

4 試驗驗證

4.1 算例分析

以過分相場景類中的F510000-TC01案例作為示例，對本文方法進行應用驗證。其中F510000代表功能特征號為510000(過分相功能)，TC01代表測試案例編號為01。車輛參數選用8節車輛編組的CRH2型列車參數，并假設列車處于平直無坡道的線路上運行。

測試目標：列車接收到應答器過分相預告信息，驗證車載設備實現自動過分相控制。F510000-TC01的主要測試步驟見表4。

表4 F510000-TC01主要測試步驟

如圖3所示，列車在A點處開始執行測試案例，測試人員驗證DMI顯示當前模式為“完全”，調整列車速度vA=100 km/h；列車運行L1(200 m)后，到達B點，列車收到【ETCS-68】包，測試人員檢驗DMI輸出分相區預告圖標，TIU輸出過分相選擇信號；列車繼續運行L2到達C點，此時車頭距分相區起點約10 s，測試人員驗證DMI輸出兩遍“前方過分相”語音提示,TIU輸出過分相命令信號，列車斷開主閘，進入惰行狀態；保持列車自動過分相，列車駛出分相區后一定距離到達F點，測試人員驗證TIU撤銷過分相命令信號，列車合上主閘，恢復牽引，進入巡航狀態；列車繼續向前運行至G點(距離分相區終點約600 m)，測試人員檢查TIU停止輸出過分相選擇信號及JRU相關信息包的記錄，在驗證過程中，列車繼續向前運行距離L4，到達H點，測試案例執行結束。

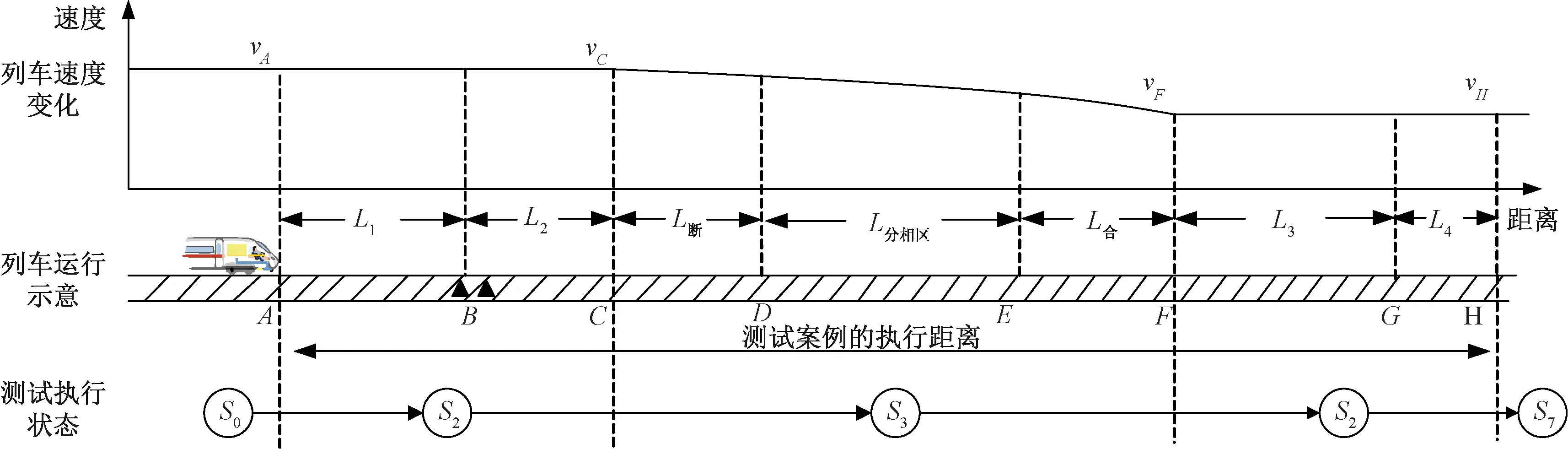
圖3 測試案例執行過程分析

4.2 有效性評估

為進一步驗證本文方法的有效性，采用隨機抽樣方法，以技術規范所定義的功能特征為劃分，從現場測試案例庫中選取測試案例進行執行距離估算。所選取的測試案例涵蓋了應答器報文接收、動態速度曲線計算、速度監控、速度與距離計算、最限制速度曲線計算、軌道電路信息接收和使用等規定的功能特征，覆蓋列車自動過分相、等級轉換、模式轉換、調車作業等規定的運營場景。本文采用實驗室車載測試平臺對所選測試案例進行實際執行和對比分析。其中，線路條件取坡度為0‰的平直軌道，線路限速為200 km/h，車輛參數為CRH2型動車組標準參數[12]。本文方法估算的距離與實際執行距離對照情況見表5。

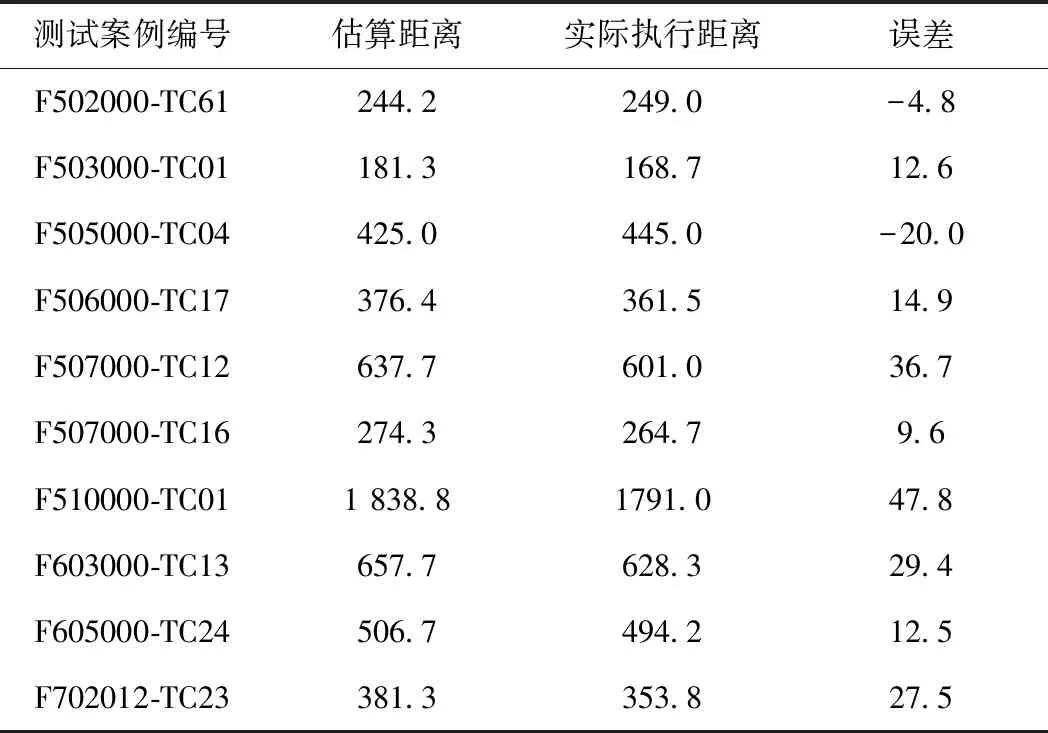
表5 本文方法估算的距離與實際執行距離對照情況 m

從表5可以看出，以實際執行距離作為參考標準，本文估算結果與實際執行距離之間的誤差絕對值控制在了50 m以內，體現出本文所提方法具備有效性。在此基礎上，本文從方法的估計誤差粒度入手，與現場測試的各種最不利指標進行比對，從而對本文方法的有效性進行進一步分析。

具體地，現場測試通常涉及到長度/距離等特征的元素包括軌道區段長度、列車長度、列車緊急制動和常用制動距離等，取本文實驗相同的CRH2型動車組標準參數，按現場測試的最不利條件[13]，以列車最限制速度40 km/h、線路坡度為上坡35‰對現場特征元素涉及的長度/距離等進行分析計算，本方法的估計誤差粒度與各特征元素的長度/距離比較見表6。

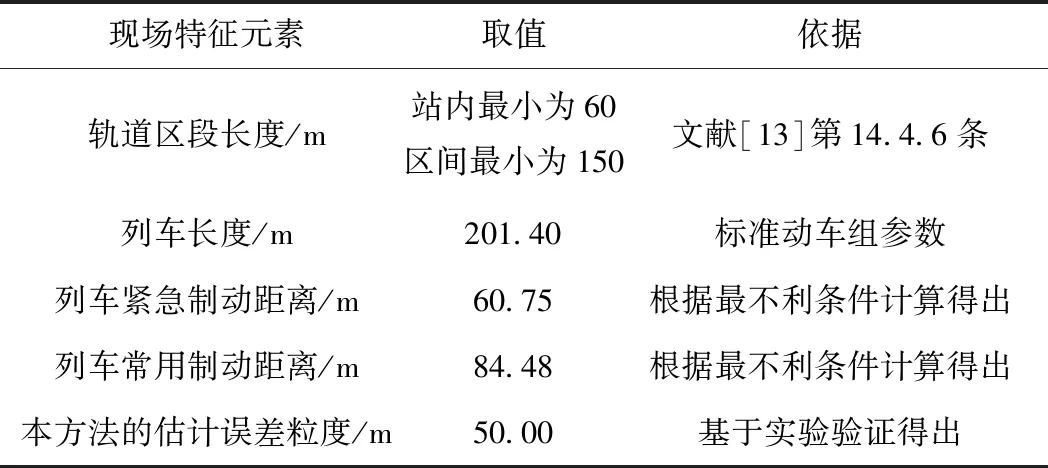
表6 本方法的估計誤差粒度與各種特征元素的長度/距離比較

分析表6可知，站內軌道區段長度是最嚴苛的現場測試特征元素，取值為60 m。在進行現場測試序列串接過程中，為保證測試的連續性，通常會預留一定距離作為誤差余量的閾值。而本方法的估計誤差粒度小于站內軌道區段長度(占比約83.33%)，意味著本文方法產生的結果誤差控制在了最嚴苛特征元素的取值范圍內，為合理選取誤差余量的閾值提供了依據，從而有利于在現場測試序列串接中控制其他變量因素(例如壓縮列車空跑距離)，提高測試效率。

5 結論

本文圍繞列控系統車載設備現場測試案例的執行距離估計問題，提出一種基于列車動力學模型的現場測試案例執行距離估算方法。從動力學的角度對現場測試案例的執行過程進行建模，將復雜的測試案例執行步驟抽象為有向圖路徑，采用動力學分析計算得到案例的執行距離。在平直軌道、線路限速為200 km/h的試驗工況下，本方法對現場測試案例的執行距離估計誤差絕對值在50 m以內，表明了本方法具備有效性，顯著提升了現場測試案例執行距離估算精度，為后續合理高效串接現場測試序列提供了有力的依據。