模塊化多電平鐵路功率調節器復合控制策略研究
宋平崗,陳 怡,雷文琪,龍日起,楊長欖
(華東交通大學 電氣與自動化工程學院,江西 南昌 330000)
隨著“一帶一路”國家戰略進一步推進以及經濟的不斷上行,貨運及客運的需求增加,交通運輸行業不斷面臨著新的挑戰與要求,高速電氣化鐵路因其運載能力強、運行速度高、準時正點及安全舒適性等優點,在世界范圍內備受青睞[1]。然而電氣化鐵路機車作為典型的單相負載,具有非線性、負荷波動幅度大、三相分布不對稱等特點,在運行過程中會產生負序和高次諧波電流,并將其注入交流電網中,從而引發電壓不對稱、三相不平衡等電能質量問題[2],這不僅給電力系統的安全穩定運行留下了隱患,而且會引起附近電力設備的擾動與誤操作。
為有效治理單相機車負載引發的電能質量問題,國內外多采用了專項專治的策略,針對不同類型的電能質量問題采取相應的措施進行治理。治理方法大體分為兩類:①對供電系統自身設備結構進行優化,其中包括引入平衡變壓器、對牽引網擴容、應用貫通式供電技術(Static Frequency Converter,SFC)[3-4]等,但此類方案工程應用性不強。②外設補償裝置,如:無源濾波器(Passive Filter,PF),但只能消除特定階次諧波且易導致諧振[5];靜止無功補償器(Static Var Compensator,SVC),但存在引入諧波電流的風險[6];全控型靜止同步補償器(Static Synchronous Compensator,STATCOM),可抑制電壓波動,但難以處理負序問題[7-8];鐵路功率調節器,憑其對牽引供電系統中電能質量問題的全面綜合治理能力,成為當前的研究熱點。其中模塊化多電平鐵路功率調節器不僅具有傳統RPC的功能,而且其模塊化程度高、開關損耗小,可以提高功率電壓等級,無需降壓變壓器即可直接接入牽引網饋線兩側[9]。
針對模塊化多電平鐵路功率調節器(Modular Multilevel Converter-railway Static Power Conditioner,MMC-RPC)的控制方法,眾多學者對其進行了研究。文獻[10]提出了一種基于微分平坦理論的直接功率控制策略,但PI控制環節較多,響應速度慢。文獻[11]針對供電臂電壓波動,提出一種多目標優化算法,在一定程度上可以抑制電壓波動,但其算法復雜,不利于大規模推廣應用。文獻[12]提出了一種基于滑模變結構的直接功率控制策略,但實際應用中難以消除滑模固有的高頻抖振。文獻[13]采用雙閉環PI控制策略,實現了有功無功的獨立控制,但不能很好地消除穩態誤差,且受非線性因素影響較大。
重復控制器的設計來源于內模原理[14],該控制器在抑制高次諧波的同時可以提高系統穩態特性。文獻[15]將重復控制器應用到有源電力濾波器中,對電流進行穩定快速跟蹤,有效降低了網側電流的諧波畸變率;文獻[16]提出一種模糊控制與重復控制相結合的PWM整流器控制策略,在提高系統抗擾能力的同時降低了穩態誤差。重復控制與RPC的治理理念不謀而合,但鮮有將重復控制應用于鐵路牽引供電系統中電能質量治理的相關研究。
本文在文獻[13]的基礎上將重復控制器應用于電流內環前饋通道中,實現對電流信號的平滑跟蹤,同時引入模糊控制對PI參數進行在線調整,提高了系統的響應速度、減小了靜態誤差并降低網側電流諧波畸變率;針對機車過渡態運行狀況下的負荷功率特性,在功率外環采用傳統PI與變參數PI相結合的分段控制策略,減小了大波動負荷電流及高頻負荷沖擊所帶來的系統超調量大的負面影響。通過在Matlab/Simulink中搭建仿真模型,驗證了所提控制策略的優越性和可行性。
1 MMC-RPC拓撲結構與補償原理
1.1 拓撲結構
鐵路功率調節器作為一種電能質量綜合補償裝置,可以達到使相間有功功率平穩流動、各饋線無功及諧波穩定補償的治理效果。MMC-RPC牽引供電系統簡化結構見圖1。圖1中,三相220/110 kV高壓經V/v牽引變壓器向供電臂輸送電壓等級為27.5 kV的單相電壓。兩個H橋型MMC(Single Phase H-bridge MMC,SPH-MMC)鏡面對稱,背靠背分別跨接于牽引饋線兩側。牽引變壓器原邊連接三相公共電網,iA、iB、iC為變壓器原邊電流;定義uj(j=L、R)為牽引網左右供電臂電壓;ij為牽引變壓器副邊電流。ijm(m=a、b)為j側供電臂流入為MMC-RPC的電流,且定義交流側等效電流is=ija-ijb。R0、L0為線路等效電阻、電感。
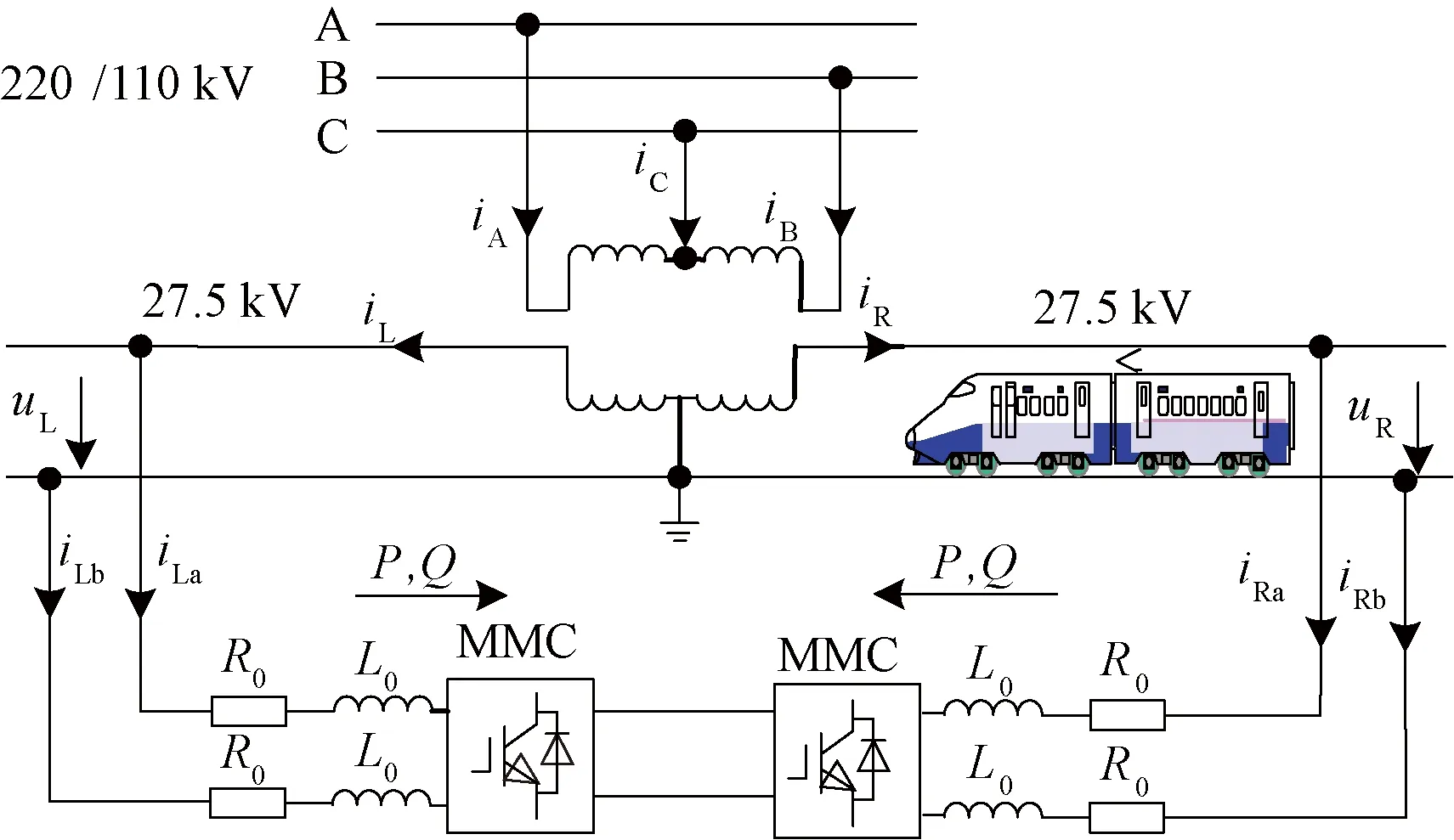
圖1 MMC-RPC牽引供電系統簡化結構
由于背靠背SPH-MMC結構對稱、功能相同,故在此只對一側進行分析建模,拓撲結構見圖2,其上下橋臂分別由N個相同的子模塊(SM)級聯而成,圖2中右側虛線為半橋SM內部結構圖。p、n分別為上、下橋臂相關表達定義。ump、umn表示m相上下橋臂子模塊電壓之和;imp、imn表示流經m相上下橋臂電流;em表示橋臂交流側端口電壓,且eab=ea-eb;us等效為左右橋臂電壓uj;udc、idc分別為直流側電壓、電流;Rs、Ls分別為橋臂等效電阻、電感。
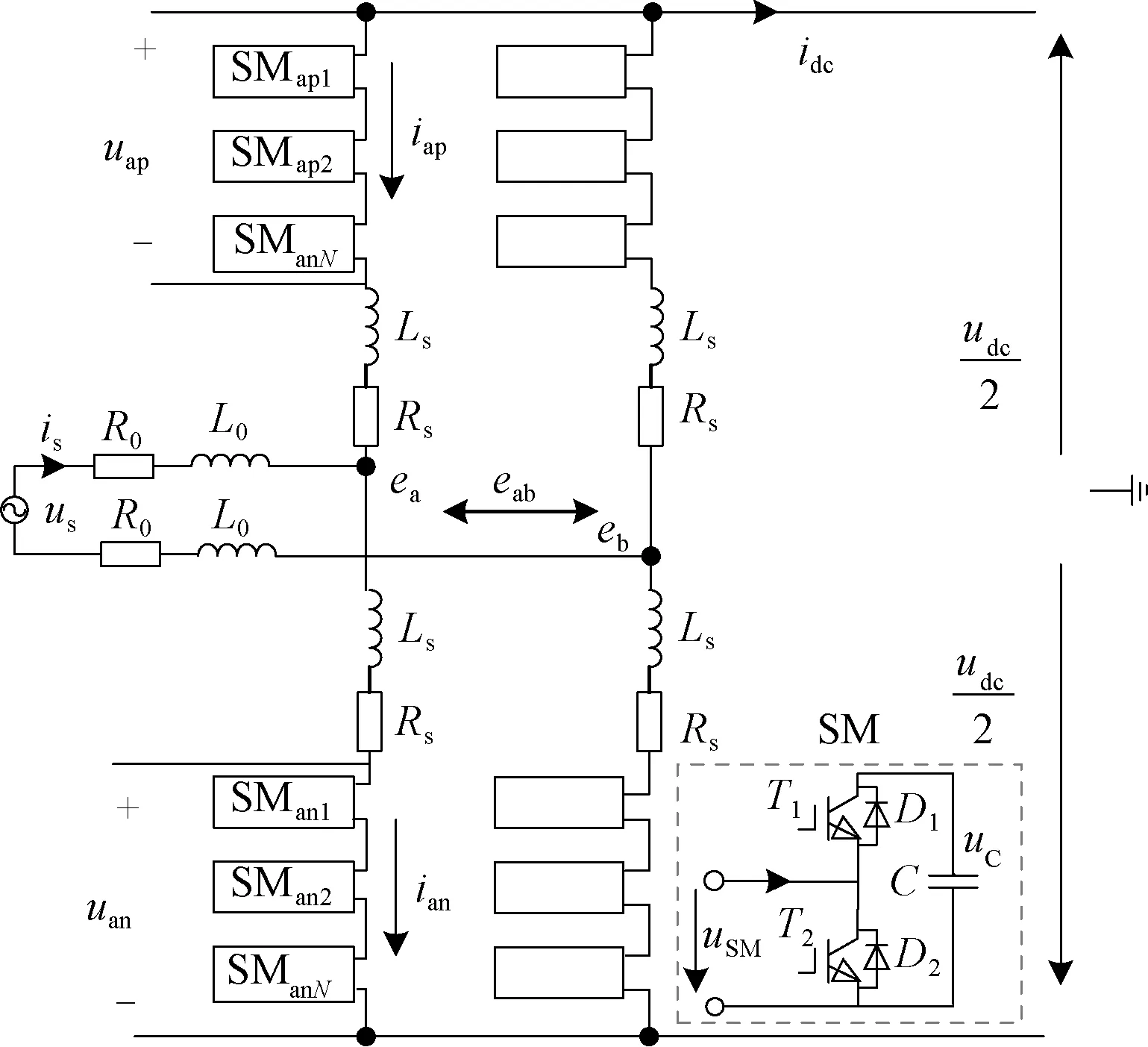
圖2 單側SPH-MMC的拓撲結構
根據KVL得出SPH-MMC交流側數學方程為
( 1 )
MMC直流側電壓方程為
( 2 )
將式( 1 )和式( 2 )相加、相減可分別得到直流側、交流端口電壓的數學方程為
( 3 )
由式( 3 )可知,可通過對SPH-MMC子模塊投切數量的管制間接控制上下橋臂子模塊的電容電壓,達到控制直流側電壓和交流側輸出端口電壓的目的,實現MMC-RPC對牽引供電系統中電能質量的就地綜合補償。
1.2 MMC-RPC功率補償原理
由V/v牽引變壓器運行中存在的較高不平衡度及兩供電臂上具有明顯不對稱性與波動性特征的牽引負荷可知,在無相關補償裝置的條件下,網側原邊電流難以時刻維持理想狀態,負序問題顯著。MMC-RPC通過平衡轉換后兩相系統間的有功并補償無功來消除原邊負序電流,達到綜合補償的目的。經RPC綜合補償前后的矢量圖見圖3。
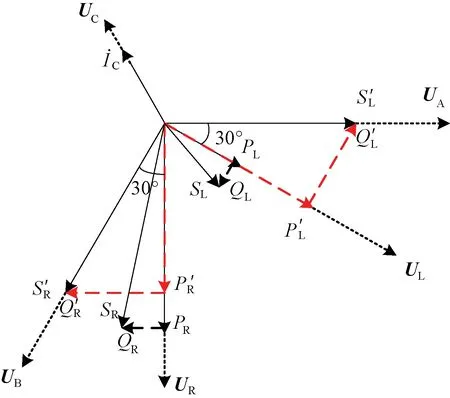
圖3 RPC功率補償前后矢量圖
圖3中,UA、UB、UC為牽引變原邊三相電壓矢量;UL、UR為副邊電壓;PL、PR、QL、QR分別為左右兩側牽引饋線負載基波有功及無功功率,其視在功率為
( 4 )
( 5 )
完成有功補償后,左右供電臂的有功功率大小相等,即P′L=P′R。若想使得原邊三相電流對稱,還需在式( 5 )的基礎上完成無功補償。同時,為了消除機車負載在運行時對牽引網注入的諧波影響,可用陷波器分離諧波電流,得出基于瞬時功率理論的畸變功率PLH、PRH、QLH、QRH。綜上所述,L、R供電臂應補償功率為
( 6 )
2 MMC-RPC控制策略
由于鐵路單相供電為單自由系統,只有一個自由度,無法直接進行同步旋轉坐標變換[17]。采用二階廣義積分[18](Second Order Generalized Integrator,SOGI)構建與實際交流量正交的虛擬分量,得到供電臂交流側電壓us以及電流is在αβ坐標系下的表達式uαβ和iαβ。單相H橋型MMC換流器交流側經αβ坐標變換后的數學模型為
( 7 )
式( 7 )經過αβ-dq坐標變換可得
( 8 )
輸入內環控制器的電流指令信號,經PI控制器解耦后產生控制輸入量,實現對單相H橋型MMC的控制。電流內環解耦控制器設計如下
( 9 )
傳統PI控制只能無靜差地跟蹤直流信號,當系統受到外界干擾時其穩態特性將會降低。在電流內環前向通道中加入重復控制器,以提高系統控制精度并有效抑制諧波信號對系統的污染。
為了得到內環電流的給定信號須引入外環控制器,在此采用定有功/無功功率控制。其設計如下
(10)
式中:P*、Q*為有功、無功功率參考值;Um為網側基波電壓幅值。
2.1 電流內環重復模糊PI控制策略
2.1.1 重復控制器設計
重復控制器的設計思想來源于內模原理。通過在控制器中嵌入一個基波周期的延時,將上一時刻的誤差信號和當前時刻的誤差信號進行累加,在提高系統的控制精度、減小穩態誤差的同時,對電流中的主要諧波可以做到有效抑制[15]。重復控制器傳遞函數為
(11)
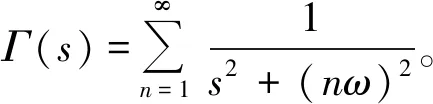
由式(11)可知,重復控制器具有多個諧振點,能夠有效抑制n次諧波對系統造成的影響。對式(11)進行離散化處理后得到傳遞函數為
(12)
式中:N為重復控制器的內模參數,N=fs/f,其中fs為系統的采樣頻率。
理想狀態下的重復控制器設計原理見圖4,其中Gp(z)為被控對象。
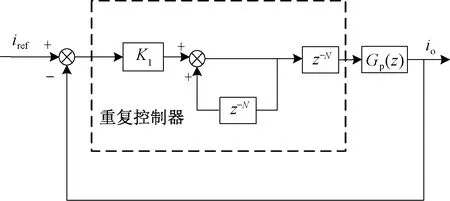
圖4 理想狀態下重復控制器原理
當重復控制器的內模輸出信號受到擾動信號的干擾時,易導致被控對象的輸出信號無法跟蹤系統指令信號,存在致使系統失去穩定性的風險。因此實際應用中重復控制器設計為圖5的形式。圖5中Q(z)為改善系統穩定性的函數,既可以為低通濾波器,也可以取小于1的常數;Gc(z)為補償函數。
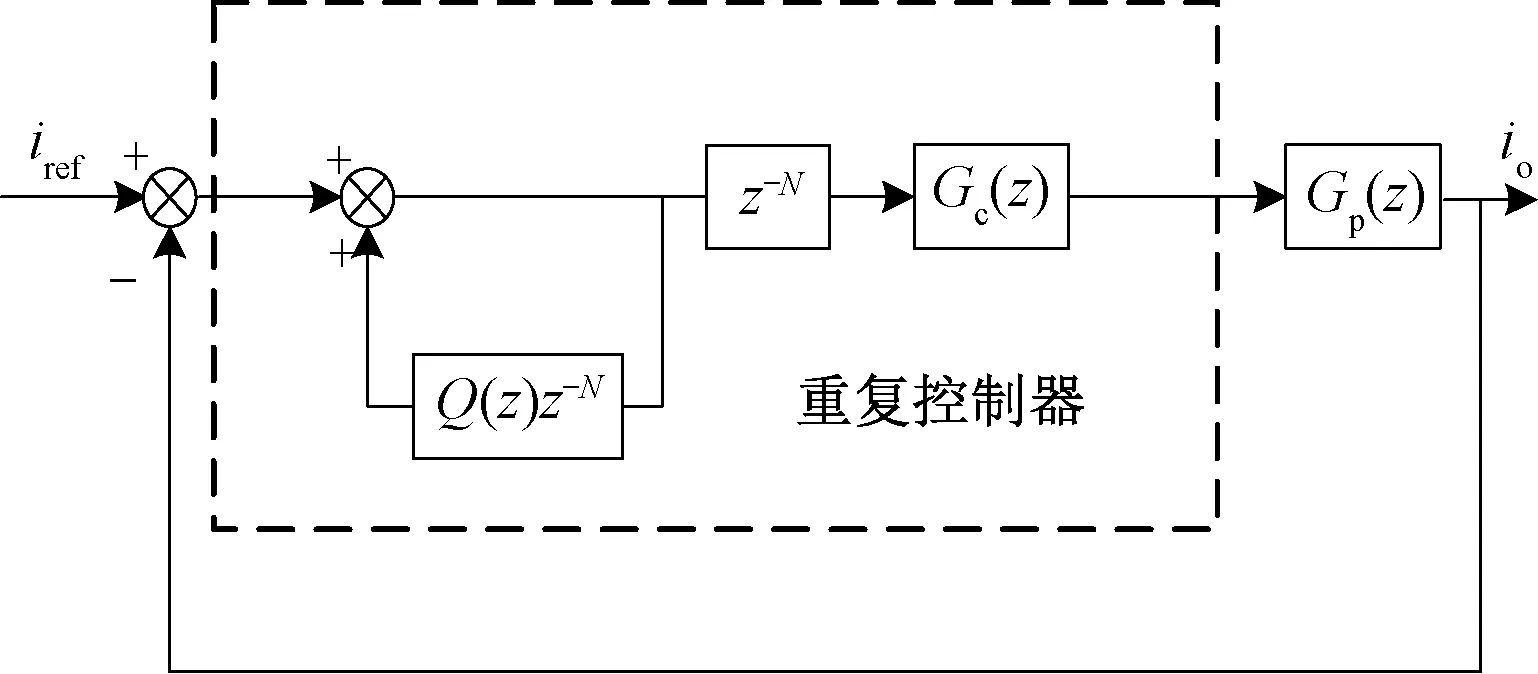
圖5 實際重復控制器原理
由圖5可得系統的閉環傳遞函數為
(13)
系統穩定的充要條件是Φ(z)的所有閉環極點位于單位圓內。設Φ(z)的特征多項式為D(z),即
D(z)=1-Q(z)z-N+z-NGc(z)Gp(z)
(14)
令D(z)=0,可得
|z|N= |Q(z)-Gc(z)Gp(z)|
(15)
令H(z)=Q(z)-Gc(z)Gp(z),由式(15)可知,系統穩定的充分必要條件為H(z)在全頻段位于單位圓內。
2.1.2 模糊PI控制器設計
傳統重復控制器在誤差補償時存在單位周期的延時,系統存在動態響應慢、抗電網波動能力差的弊端[19]。為了提高系統的動態性能,本文以將PI控制器和重復控制器相結合的方式來設計內環控制器。文獻[20]提出一種并聯型PI+重復控制方案實現對LCL逆變器的控制,但該方案的控制系統設計復雜,實際應用難度大。因此,提出一種串聯型PI+重復控制的復合控制器結構,使重復控制的輸出加在PI控制的給定值上,在保證諧波抑制效果的同時滿足了系統的穩定性要求。由于傳統PI控制器參數難以整定,當系統發生擾動時,容易失穩。在此引入模糊控制對PI控制器參數進行在線調整,使得調節范圍更寬,提高了系統的魯棒性,改善了系統的控制性能。模糊PI+重復控制器控制框圖見圖6。
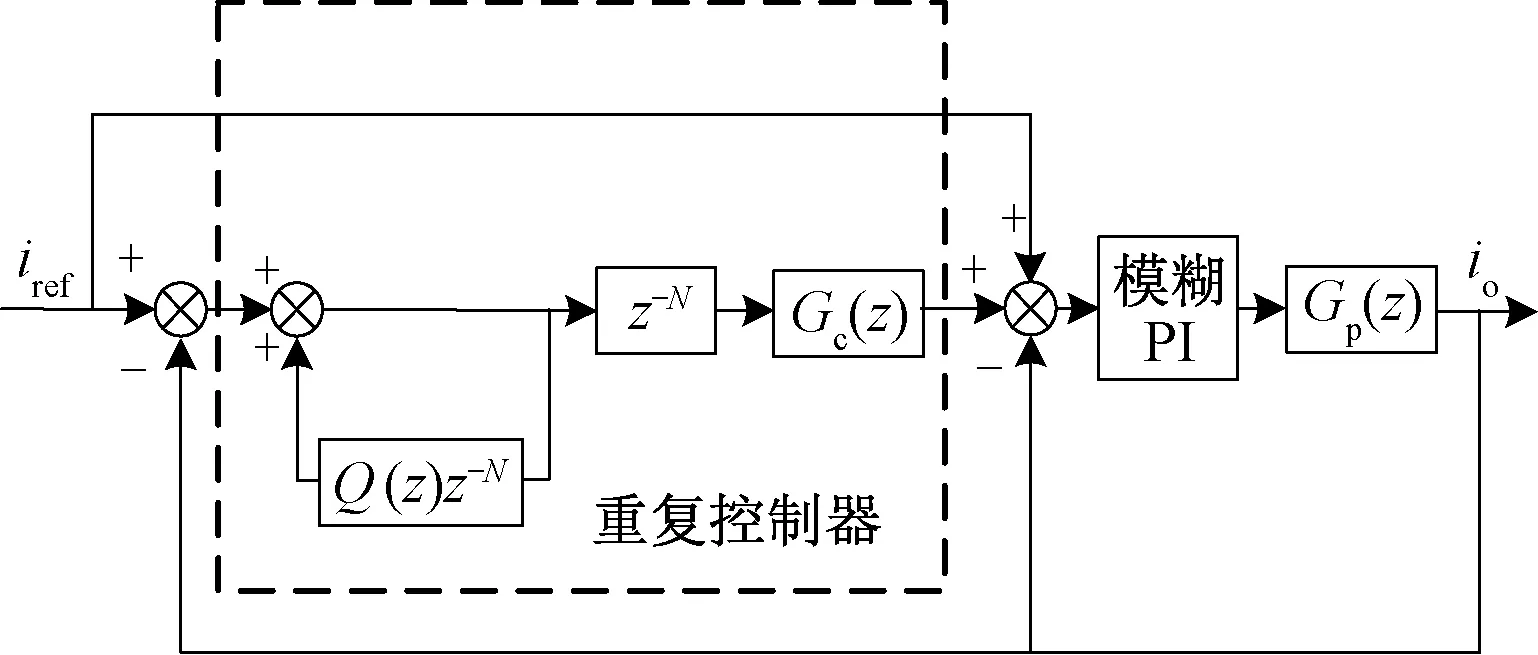
圖6 模糊PI+重復控制器控制框圖
2.1.3 重復控制器參數設計
為了達到最優控制效果,需對重復控制器的相關參數進行合理設計。
為實現電流環的穩定無靜差控制,應確保|Q(z)|<1。通常情況下將Q(z)設計成低通濾波器或者小于1的常數。經過仿真試驗,最終確定當Q(z)=0.95時,系統可以獲得良好的響應。系統采樣頻率fs=10 kHz,每周期采樣次數N=fs/f=200。
補償器Gc(z)用來補償被控對象Gp(z)的幅值和相位,增強系統的穩定裕度,提高控制精度。
Gc(z)=KrzkS(z)
(16)
式中:Kr、zk分別為補償被控系統的幅值、相位。
假設僅有重復控制器作用于被控對象,則電流環被控對象可看作一階慣性環節。其在s域的表達式為
(17)
式中:L為電感,L=1 mH;R為等效電阻,R=0.5 Ω。
將被控制對象經過零階保持器進行離散化處理得到
(18)
系統的采樣頻率為fs=10 kHz,代入式(18)可得
(19)
進而可得被控對象的閉環傳遞函數Φp(z)為
(20)
閉環傳遞函數Φp(z)Bode圖見圖7。由圖7可知,Φp(z)在中低頻段的幅頻特性不為1,在中高頻段幅值衰減緩慢,且存在明顯相位滯后,嚴重影響了系統動態響應的實時性。
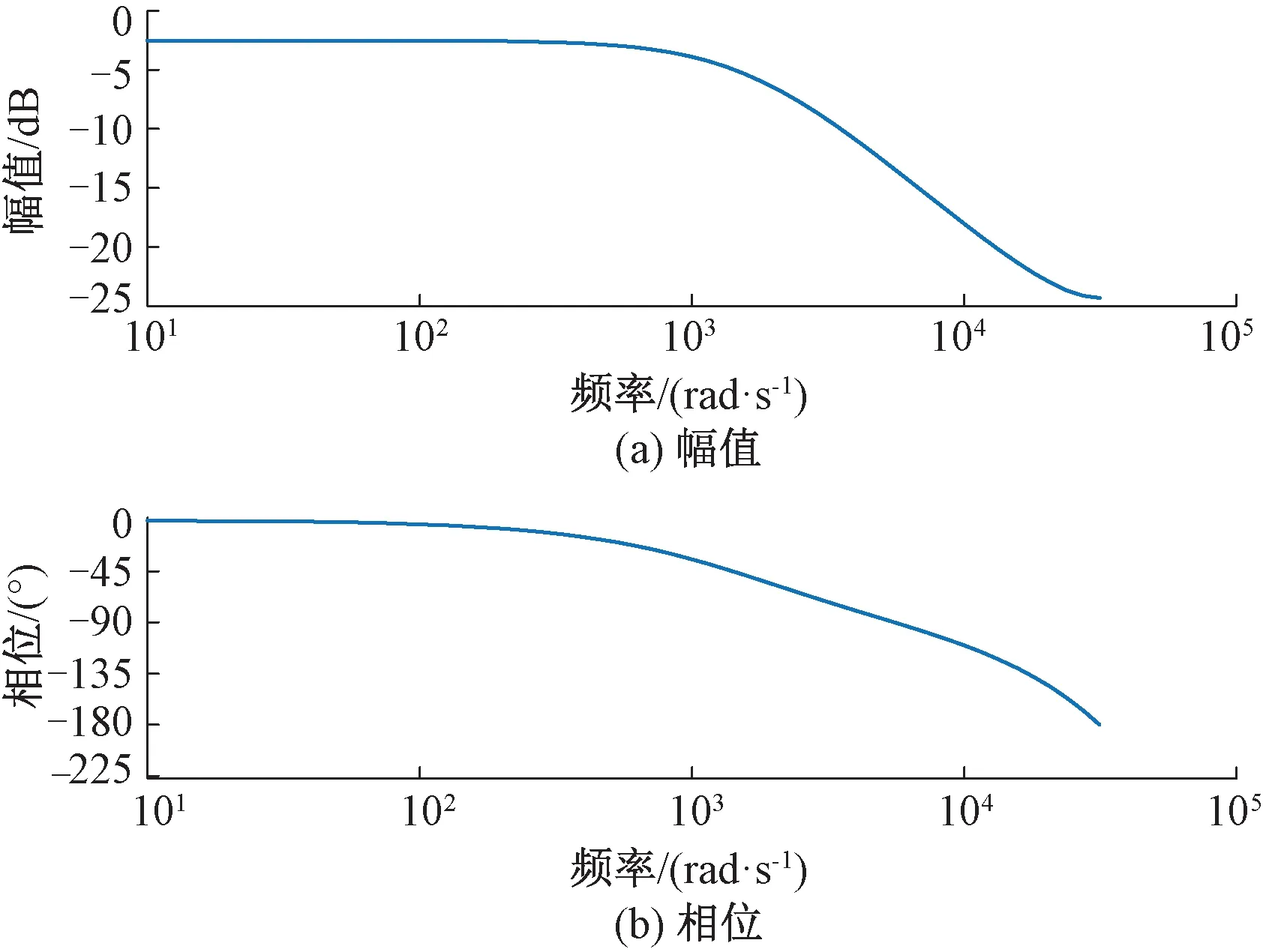
圖7 閉環傳遞函數Φp(z)Bode圖
由于高頻段相位滯后嚴重且難以校正,本文采用二階低通濾波器S(z)對高頻段幅值進行加速衰減,以此消除高頻諧波的干擾。參考文獻[16],濾波器的轉折頻率取開關頻率的1/5,系統阻尼比取最佳為0.707。則離散狀態下的二階低通濾波器設計為
(21)
補償效果下KrS(z)Φp(z)的Bode圖見圖8。圖8中幅值補償系數Kr=1.45。
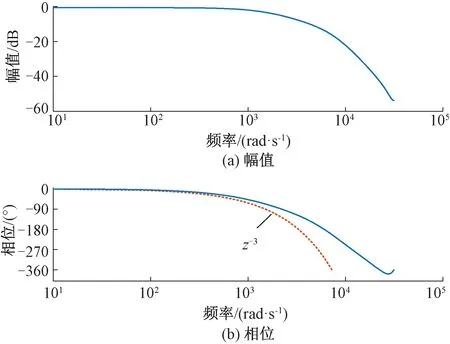
圖8 補償效果下KrS(z)Φp(z)的Bode圖
對比分析校正前后的Bode圖可知,補償后中低頻段增益為1,且在中高頻段可以快速衰減幅值,從而減少高頻諧波的干擾。但分析校正后的相頻特性曲線可知,系統相位滯后比較嚴重,需通過相位補償器zk進行相位補償。圖8相頻特性曲線中的虛線表示z-3的相頻特性曲線,可以看出中低頻段其相位能與KrS(z)Φp(z)保持一致,在此引入超前環節z3對相位進行補償,使電流能夠準確跟蹤給定信號。
由式(15)可得系統的特征根表達式為
H(z)=0.95-1.45z3S(z)Φp(z)
(22)
系統穩定的充要條件為H(z)在全頻段內的所有特征根位于單位圓內。為檢驗系統的穩定性,繪制1.45z3S(z)Φp(z)和單位圓的Nyquist曲線見圖9。由圖9可知,1.45z3S(z)Φp(z)的Nyquist曲線包含在以(0.95,0)為圓心的單位圓內,因此設計系統滿足穩定性條件。
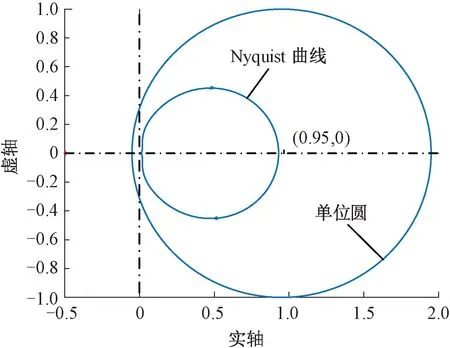
圖9 1.45z3S(z)Φp(z)和單位圓的Nyquist圖
2.1.4 模糊控制器參數設計
模糊PI控制,即根據模糊邏輯和一定的模糊規則對Kp和Ki進行在線優化,以克服傳統PI控制器不能進行參數實時調整的弊端。模糊PI控制器主要由參考電流與輸出電流的誤差E以及誤差變化率Ec的模糊化、確定模糊規則、解模糊等部分組成,其輸出量為PI控制器參數Kp和Ki。模糊PI控制框圖見圖10。
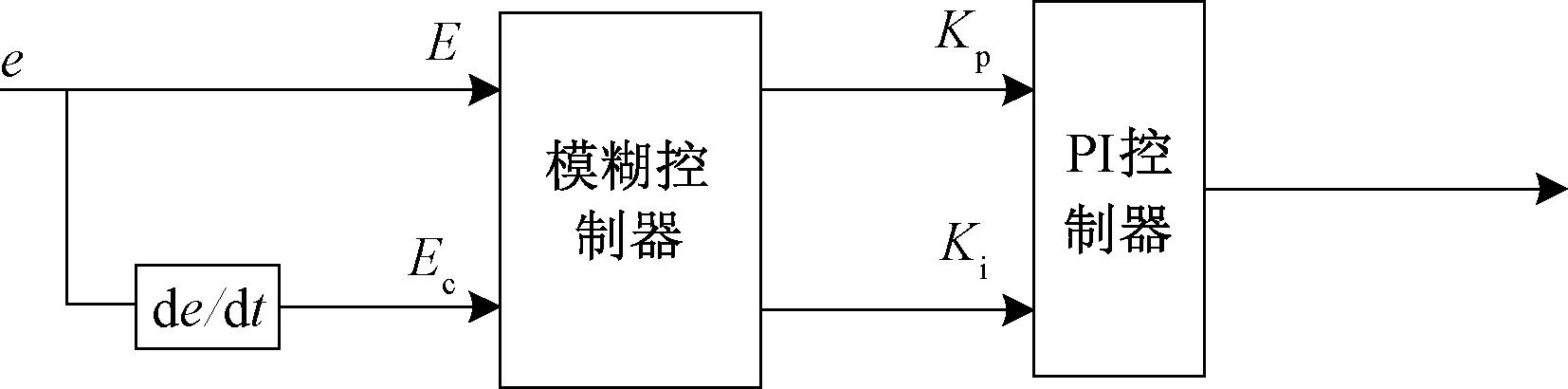
圖10 模糊PI控制框圖
令Ed、Ecd和Eq、Ecq為電流環d、q軸的誤差和誤差的變化量;kp、ki為Kp、Ki模糊變量。相關參數見表1。其隸屬度函數包含7個模糊子集(NB,NM,NS,ZE,PS,PM,PB),隸屬度函數采用三角型。

表1 模糊控制器參數
模糊規則表見表2。采用重心法進行解模糊獲得d/q的PI控制器的參數。
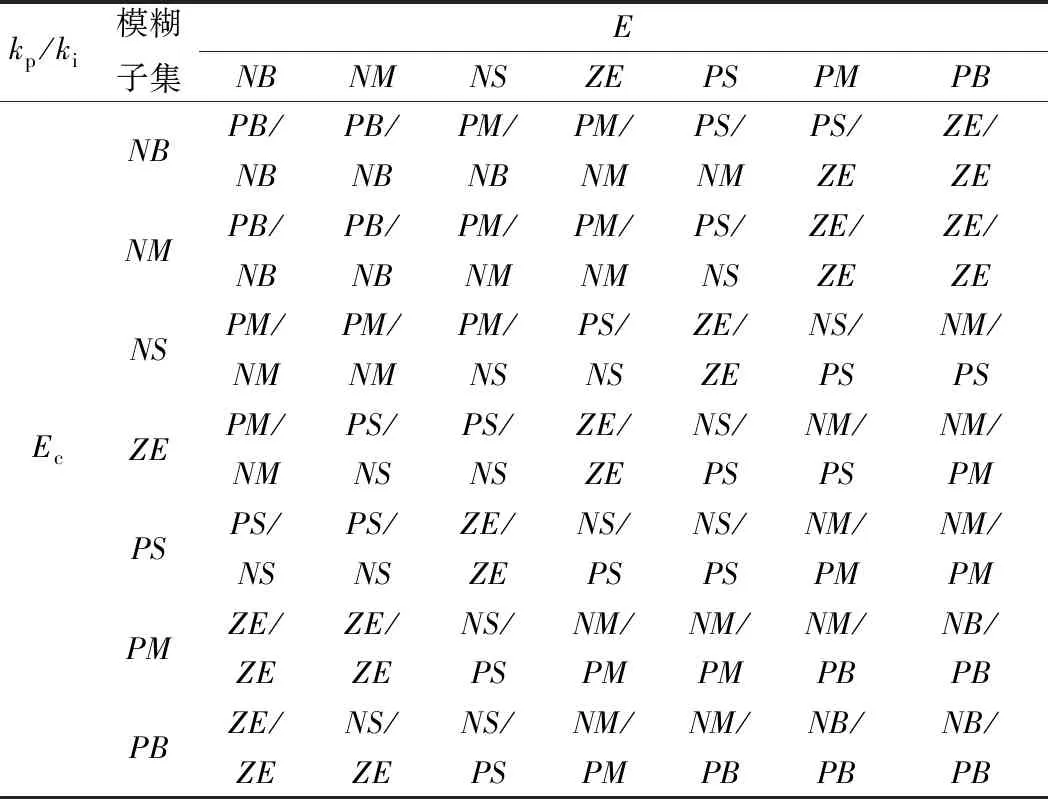
表2 模糊控制規則表
2.2 功率外環復合PI控制策略
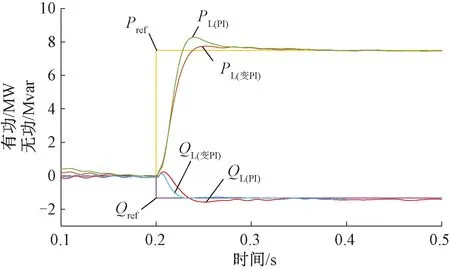
功率外環的控制對內環電流的跟蹤特性有一定的影響。傳統PI控制通過選取比例積分增益來使系統實現所需的動靜態性能:隨著Kp的增加,系統響應速度加快,但是容易出現震蕩,不利于系統穩定運行;Ki用于減小系統的靜態誤差,Ki越小,系統的靜態精度越高,但超調量也會隨之增大,反之,Ki越大將導致系統的靜態精度不夠,尤其當系統處于大偏差階段時,Ki會使系統出現大的超調現象[21]。常規PI參數不能根據被控對象的實時情況進行動態調整,難以適應鐵路機車移動單相可變負載的運行工況。為克服這一缺點,本文設計一種由傳統PI與變參數PI相結合的分段PI控制策略來實現對功率外環的穩定控制。復合PI控制框圖見圖11(以定有功功率控制為例)。通過給誤差開關S設置閾值Es(取穩態誤差的1.5倍)對有功功率進行分段控制。當誤差|e|>Es時,判斷有功功率處于過渡過程,誤差開關S切換至變參數PI控制模式;當|e|≤Es時,判斷有功功率處于穩態過程,誤差開關函數切換至傳統PI控制模式。
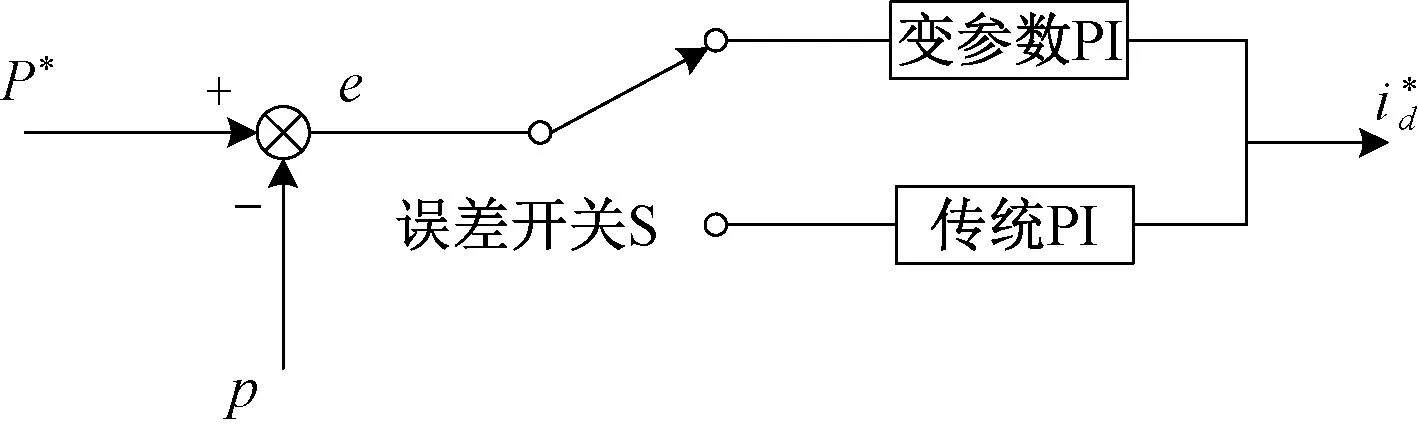
圖11 復合PI控制框圖
在有功功率響應處于過渡階段時,有功功率參考值與實際輸出值誤差較大,系統超調量大,響應速度慢,此階段采用變參數PI控制。取Kp、Ki為誤差e的函數,當誤差變大時,Kp增加,系統響應速度提高;當誤差逐步變小時,Kp減小的同時Ki增加,使系統能夠快速無超調地達到有功功率給定值。變參數PI控制設計關于誤差e的函數表達式[22]為
(23)
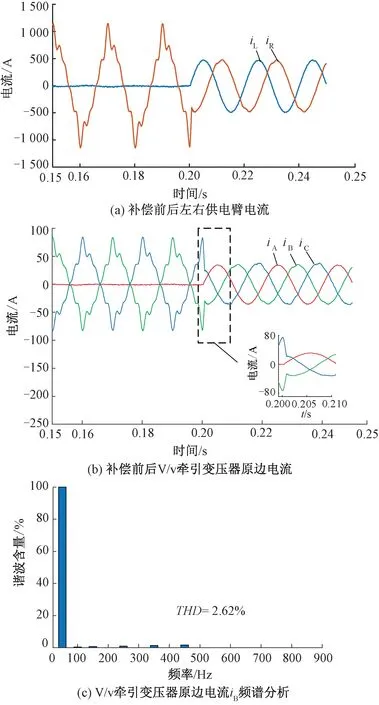
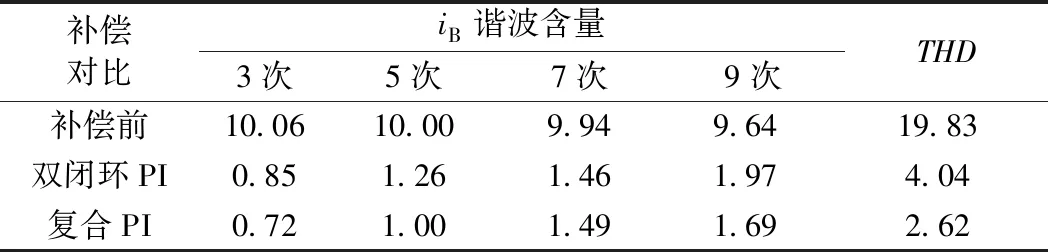
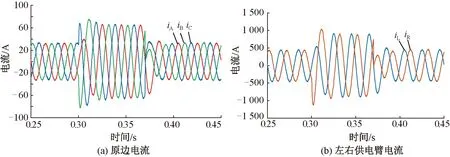
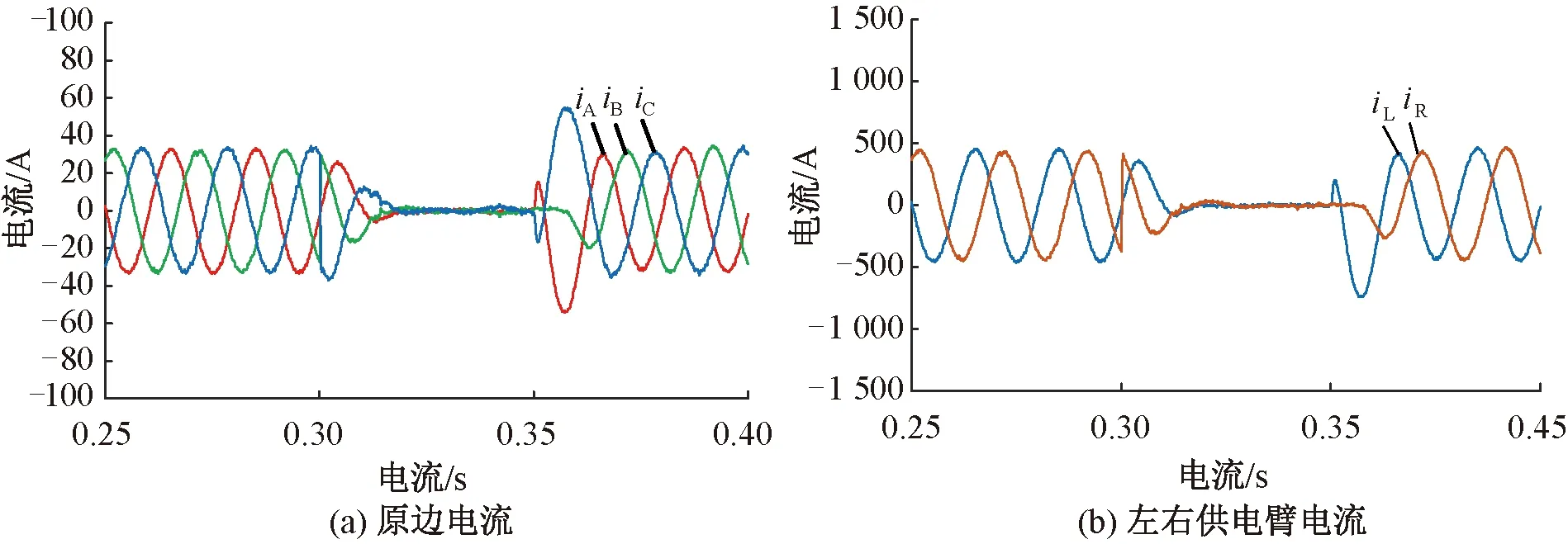
式中:kp0、ki0為比例積分增益的初始值kp0=ki0=1×10-5;k1、k2為修正系數。一般取0 綜上可得MMC-RPC的整體控制框圖見圖12。 圖12 基于復合控制策略的MMC-RPC控制框圖 為驗證所提控制策略的優越性和有效性,在Matlab/Simulink仿真軟件中分別搭建基于復合控制策略以及傳統雙閉環PI控制下的MMC-RPC仿真模型并進行對比分析。模型參數見表3。 表3 仿真模型主要參數 為驗證本文所提控制策略下的MMC-RPC的治理補償效果,仿真模擬V/v牽引變壓器處于最大不平衡工況下的功率補償,即僅存在一側供電臂有電力機車負載運行(采用右側供電臂)。 右側供電橋臂機車負載SR_load1=(15+j3)MV·A,并向牽引網注入幅值為80 A的3、5、7、9次諧波。在仿真運行到0.2 s時投入MMC-RPC進行治理,并與傳統PI雙閉環控制下的治理效果進行對比。 在實際牽引供電系統運行狀態中,鮮有單一供電臂有負載的情況,牽引負荷一般分散于牽引變壓器的整個供電區間且兩供電臂負載間無較大偏差。仿真模擬的設計是為了驗證所提控制策略下的MMC-RPC在應對V/v牽引變壓器不平衡狀態極為嚴重情況下的補償治理能力。 3.1.1 原邊電流、左右供電臂電流波形分析 傳統雙閉環控制的波形見圖13;復合控制策略下的波形見圖14。 圖13 MMC-RPC傳統雙閉環PI控制補償電流分析 圖13(a)、圖13(b)與圖14(a)、圖14(b)分別為傳統雙閉環PI控制與復合控制策略下補償前后左右供電臂電流iL、iR以及V/v牽引變壓器原邊電流iA、iB、iC的波形圖。在0.2 s時,MMC-RPC投入運行,兩種控制策略都能實現負序治理的效果,使左右供電臂和三相電流達到平衡。但是傳統雙閉環PI控制在MMC-RPC投入瞬間,三相電流存在小幅度波動,而采用復合控制策略時,能相對平穩快速地進入負序治理狀態,輸出電流波形呈現出較好的正弦性。 圖13(d)與圖14(c)分別為傳統雙閉環PI控制與復合控制策略下補償后V/v牽引變壓器原邊電流iB的頻譜分析圖。MMC-RPC未投入運行、傳統PI控制下以及本文所提的復合PI控制下MMC-RPC投入運行后V/v牽引變壓器原邊電流iB的各次諧波含量以及THD值的比較結果見表4。由表4可知,傳統雙閉環控制輸出電流畸變率較高為4.04%,復合控制策略下畸變率為2.62%,降低了1.42%,輸出波形質量得到了有效改善,同時可以看出復合控制策略對諧波的治理能力優于傳統PI控制。 圖14 MMC-RPC復合控制策略下補償電流分析 表4 補償前后電流iB各次諧波電流含量及THD值 % 3.1.2 左側供電臂功率波形分析 為驗證變參數PI在提高系統控制精度上的優越性,在0.2 s時,將MMC-RPC投入運行,此時相當于給系統加入一個“擾動”,來分析變參數PI控制的波形,與傳統PI控制的波形對比分析。 補償前后傳統PI雙閉環控制和變參數PI控制策略下左側供電臂傳輸功率波形見圖15。由圖15可知,兩種控制策略均能穩定功率的傳輸,但傳統雙閉環PI控制下功率波動范圍較大,存在穩態誤差。而本文所提控制策略下,在RPC投入運行后,功率可以迅速無超調地達到參考值,且波動小,跟蹤控制效果好。兩種調節器的控制性能的對比見表5。 圖15 補償前后MMC-RPC供電臂功率波形 表5 兩種調節器控制性能的對比 3.1.3 直流側電壓波形分析 由于MMC-RPC由兩個單相H橋結構的MMC背靠背連接構成,要求控制系統要能夠很好地控制直流電壓的穩定。本文所提控制策略和傳統PI雙閉環控制下的直流側電壓波形見圖16。 圖16 兩控制策略下直流側電壓波形對比 由圖16可知,兩種控制方法都能對直流側電壓進行有效控制,分析其局部放大圖可知,相對于傳統PI,復合控制下的電壓波動幅度小,控制效果更佳。 為進一步驗證基于復合控制策略下的MMC-RPC在牽引供電系統中的電能補償治理效果,對以下兩種工況進行仿真分析。 工況1:為驗證所提控制策略下MMC-RPC應對負載投切時的治理效果,在3.1節仿真的基礎上,分別在0.30、0.37 s時刻對增加的機車負載SR_load2=(15+j3)MV·A進行投入和切除。 工況1下負載投入和切除時V/v牽引變壓器原邊電流以及左右供電臂電流仿真波形見圖17。0.3 s時左供電臂負載SR_load1=(15+j3)MV·A突變為(30+j6)MV·A,V/v牽引變壓器原邊電流從33 A增加為66 A;0.37 s時電流隨著負載的切除恢復至原值。無論負載在投入還是切除時,調整V/v牽引變壓器補償電流時間均小于0.5個周期,使得系統快速達到三相平衡。說明本文所提控制策略下MMC-RPC可以適應負載突變時的功率補償。 圖17 負載突變時V/v牽引變壓器原邊電流、左右供電臂電流 工況2:為驗證所提控制策略下MMC-RPC應對潮流反轉時的控制效果,在RPC投入運行的情況下,0.3 s時機車負載SR_load1=(15+j3)MV·A從右側供電臂過分相轉移到左側供電臂。 工況2下潮流翻轉即負載換相時V/v牽引變壓器原邊電流以及左右供電臂電流仿真波形見圖18。0.3 s時機車負載進入分段換相區(供電死區),0.35 s時右側負載SR_load1=(15+j3)MV·A轉移到左側供電臂,潮流發生反轉,所提控制策略下的MMC-RPC能夠在0.02 s內應對負載過分相,補償V/v牽引變壓器使得電流快速恢復平衡。 圖18 負載換相時V/v牽引變壓器原邊電流、左右供電臂電流 文章針對V/v牽引供電系統中電力機車運行時產生的負序和諧波電流問題,提出一種復合控制策略的MMC-RPC控制策略。通過仿真分析得出以下結論: (1)設計在相同參數及運行工況下,對比復合控制策略與傳統PI控制對電能質量問題的治理效果。相對于傳統PI控制,復合控制下的V/v牽引供電系統可以實現對電流的實時平滑準確跟蹤,系統響應速度更快,THD值更低,功率波動范圍更小,其不平衡度為0,可以實現單位功率因數運行;對控制參數進行動態調整,動態性能好,增強了系統的抗干擾能力。 (2)在極端工況下,如機車負載發生突變或潮流發生反轉時,本文所提控制策略下的MMC-RPC能夠迅速響應,使系統快速達到平衡狀態,治理效果顯著,有利于RPC適應于鐵路負載多變、非線性、復雜的運行環境。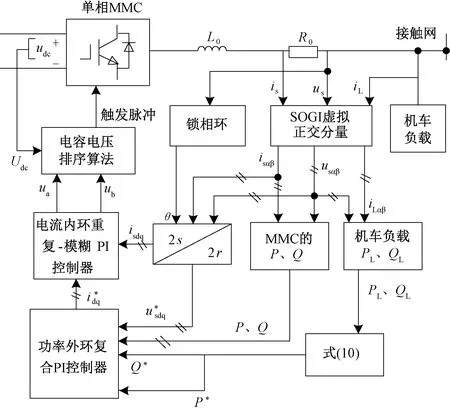
3 仿真分析

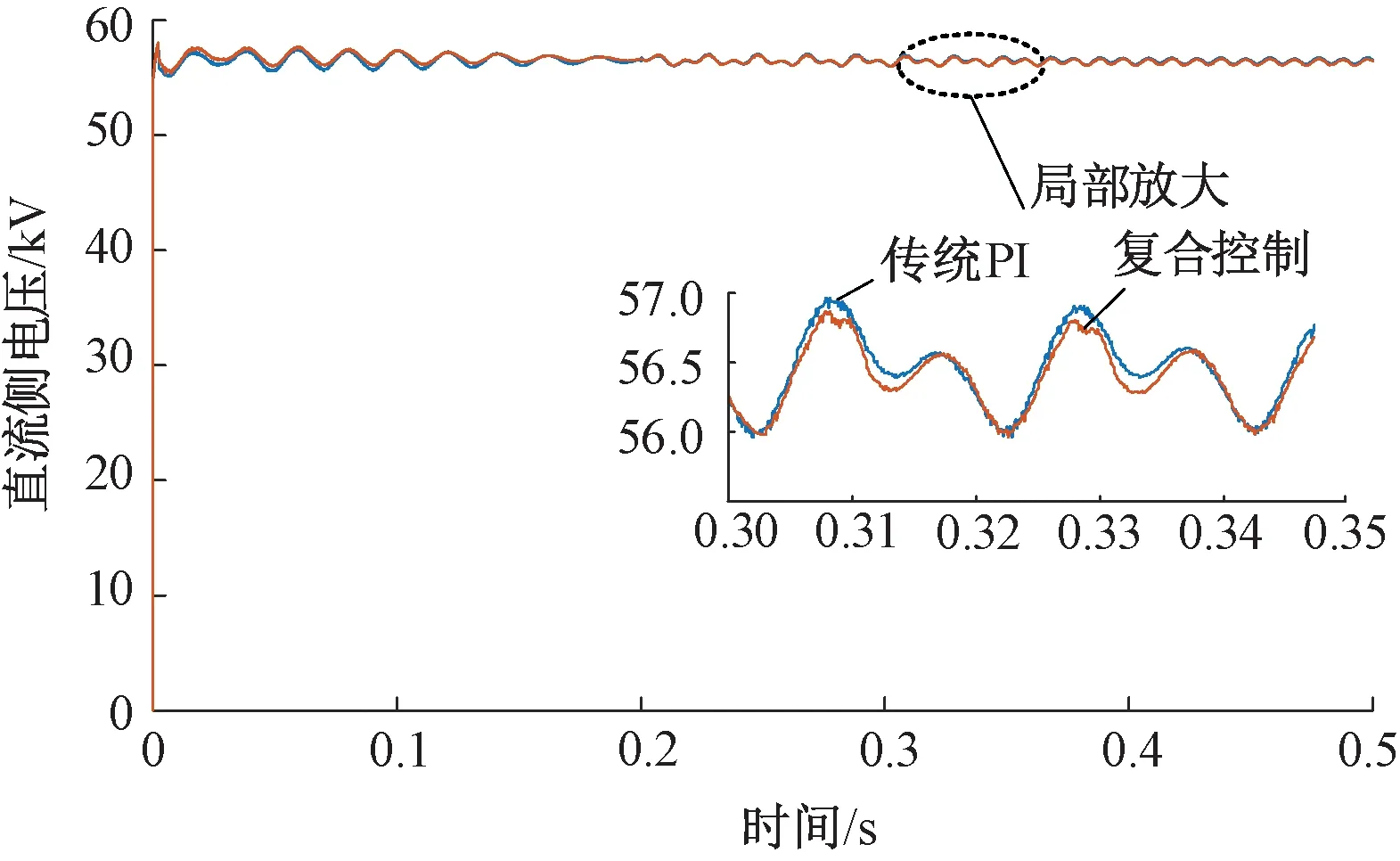
3.1 電流、功率、直流側電壓波形分析


3.2 兩種工況下復合控制策略仿真分析
4 結論

