基于非線性理論的接觸網找形方法研究

羅 群，梅桂明，趙 晨，王江文，邱江洋，韓寶峰

(1.西南交通大學 牽引動力國家重點實驗室,四川 成都 610031；2.廣東交通職業技術學院，廣東 廣州 510650；3.中車青島四方機車車輛研究所 重慶研發中心，重慶 401133；4.保德利電氣設備有限責任公司，陜西 寶雞 721000)

高速列車通過車頂受電弓與接觸網穩定接觸以獲取電能，進行電力牽引，其運行性能很大程度上取決于受電弓與接觸網之間的動態相互作用[1-2]。而深入開展受電弓與接觸網動態相互作用的仿真計算研究，對高速列車運行性能的提升有著重要作用[3]。近年來，針對這一課題，建立了不同的仿真計算模型用來模擬受電弓與接觸網的動態相互作用關系，其建模方法主要分為兩種：基于絕對節點坐標法(ANCF)的有限元方法[4-7]以及空間有限元法[8-10]。但無論是仿真模型還是建模方法的選擇，接觸網系統的初始平衡構型將會對仿真結果產生極大的影響[11-12]。因此，仿真前準確獲得接觸網系統的初始平衡構型顯得尤為重要。

通過坐標系描述的接觸網系統幾何形貌稱為接觸網構型[13]，接觸網系統在其自身重力、張力體系以及邊界條件的約束下將形成預設弛度的內應力平衡的初始構型[14]，而確定這一滿足平衡的初始構型的過程，稱為找形[13]。目前，找形中使用較多的分析方法為非線性位移法[15]和力密度法[16]。非線性位移法即在所求結構的幾何變化的基礎上，尋找達到規定力分布的平衡構型。該方法從初始力分布、懸索之間的連續性以及邊界條件，獲得初始應力構型和內應力分布。而力密度法，則是通過規定力密度，將懸索節點坐標的非線性平衡方程轉換為線性方程組。

在上述分析方法的基礎上，國內外學者提出了多種具體的接觸網找形方法。文獻[4]提出利于求解懸索等大變形結構的ANCF方法進行接觸網找形，其考慮了接觸網兩節點有限元單元的軸向和彎曲變形，并通過分段方程控制張力。文獻[12]提出懸鏈線方程找形法，通過懸鏈線一般表達式，建立接觸網整體力平衡式求解其初始構型。文獻[17]采用拋物線找形，將接觸網離散為拋物線單元，建立承力索力矩平衡方程式求解承力索初始構型。文獻[9]采用有限元法找形，使用歐拉-伯努利梁單元離散接觸網，通過吊弦張力的最小誤差確定吊弦長度，最終得到接觸網的初始平衡構型。

對比上述方法，ANCF法找形結果雖然具有良好的計算精度，但單元數較多且涉及高階導數的運算，有限元法單元數也較多，求解規模均較大；對于拋物線法找形，計算過程中只考慮其線性項而忽略了非線性項，導致跨中部分吊弦長度計算結果相對誤差較大；而懸鏈線方程找形方法，其基于非線性理論，充分考慮了計算過程的非線性項，能夠準確表示吊弦與吊弦間的接觸網單元，且該方法求解規模取決于吊弦數量與控制張力數量，求解規模小，即該方法同時具有計算精度高、求解快速等優點。因此，本文將使用非線性理論下的懸鏈線方程計算獲取接觸網初始平衡構型。與文獻[12]不同地是，本文將使用懸鏈線方程的精確解析式，并結合分模法[18]的思想進行接觸網找形，即先分離求得接觸線初始平衡構型，再基于懸鏈線方程和初始構型下的單元節點力平衡關系得到承力索、彈性吊索等結構的初始平衡構型，在保證計算精度的同時，簡化了求解形式并降低了求解規模。

1 非線性基本理論

纜索的受力計算理論主要有線性理論和非線性理論，其中線性理論假定垂向載荷沿著索跨度均布，推導得到拋物線方程，而非線性理論假定垂向載荷沿著索長度均勻分布，推導得到懸鏈線方程，同時，在推導過程中假設纜索為理想柔性且其材料符合胡克定律[19]。

高速鐵路接觸網系統中接觸線、承力索以及彈性吊索均為纜索結構，重力荷載沿索長均勻分布，彎曲剛度可忽略，與非線性理論相契合。同時，文獻[20]也驗證了懸鏈線單元對含有初始彎曲的電纜建模的可靠性以及實用性。因此，可將非線性理論應用于接觸網找形，并通過懸鏈線方程表示離散的接觸網懸鏈線單元，其中包括了不等高與等高懸鏈線方程。

不等高懸索計算簡圖見圖1。圖1(a)表示荷載q沿索長均勻分布且兩端分別懸掛于AB兩點的不等高懸索，AB兩點間距為L，高度為h，索兩端張力分別為T1、T2，其分量為T1x、T1y、T2x、T2y。該懸索的任意微分單元dx受力分析見圖1(b)，Tx為索張力的水平分量。

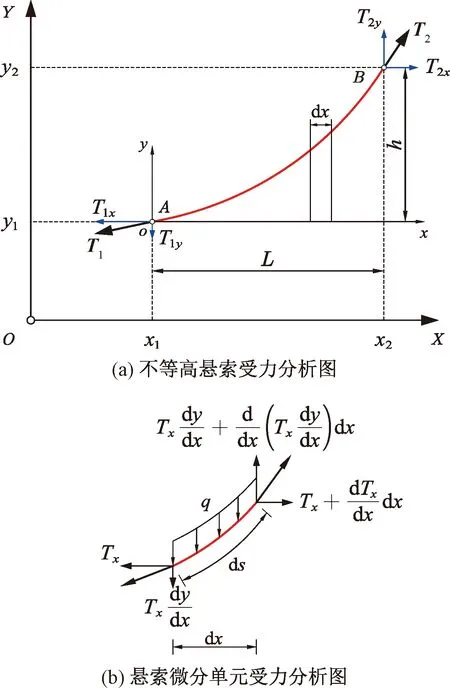
圖1 不等高懸索計算簡圖

根據微分單元的靜力平衡條件，有

( 1 )

式( 1 )可化簡為

( 2 )

式中：Tx為恒定值，并進一步的可以得到

( 3 )

求解式( 3 )可以得到坐標系oxy中懸索AB的懸鏈線方程。滿足邊界條件的解為

( 4 )

式中：D1、D2為由其余參數計算得到的常數項;C為常數，計算式為

( 5 )

同時，為便于描述各接觸網單元，并根據A、B兩端點坐標值，D1、D2又可分別定義為

( 6 )

D2=-C·coshD1

( 7 )

式中：ρ為索的線密度；g為重力加速度；(x1,y1)、(x2,y2)分別為A、B兩點坐標。

注意到式( 4 )為坐標系oxy中的懸鏈線方程，通過坐標轉換可得到全局坐標系OXY中的懸鏈線方程為

( 8 )

式( 8 )即為全局坐標系下，表示懸索AB在重力荷載沿索長分布作用下的不等高懸鏈線方程。

當A、B兩端點等高時，y1=y2，代入式( 6 )有

( 9 )

將式( 9 )代入式( 8 )則可得等高懸鏈線方程。

2 接觸網找形研究

2.1 接觸網模型

接觸網系統的懸掛導線主要由接觸線、承力索以及吊弦組成，我國高速鐵路常用的兩種結構[21]見圖2。圖2(a)為簡單鏈型懸掛接觸網，主要結構為承力索、接觸線和吊弦，長度不等的吊弦通過線夾將承力索與接觸線進行連接。與簡單鏈型懸掛接觸網相比，彈性鏈型懸掛接觸網則在承力索的兩跨之間增加了結構彈性吊索，見圖2(b)。

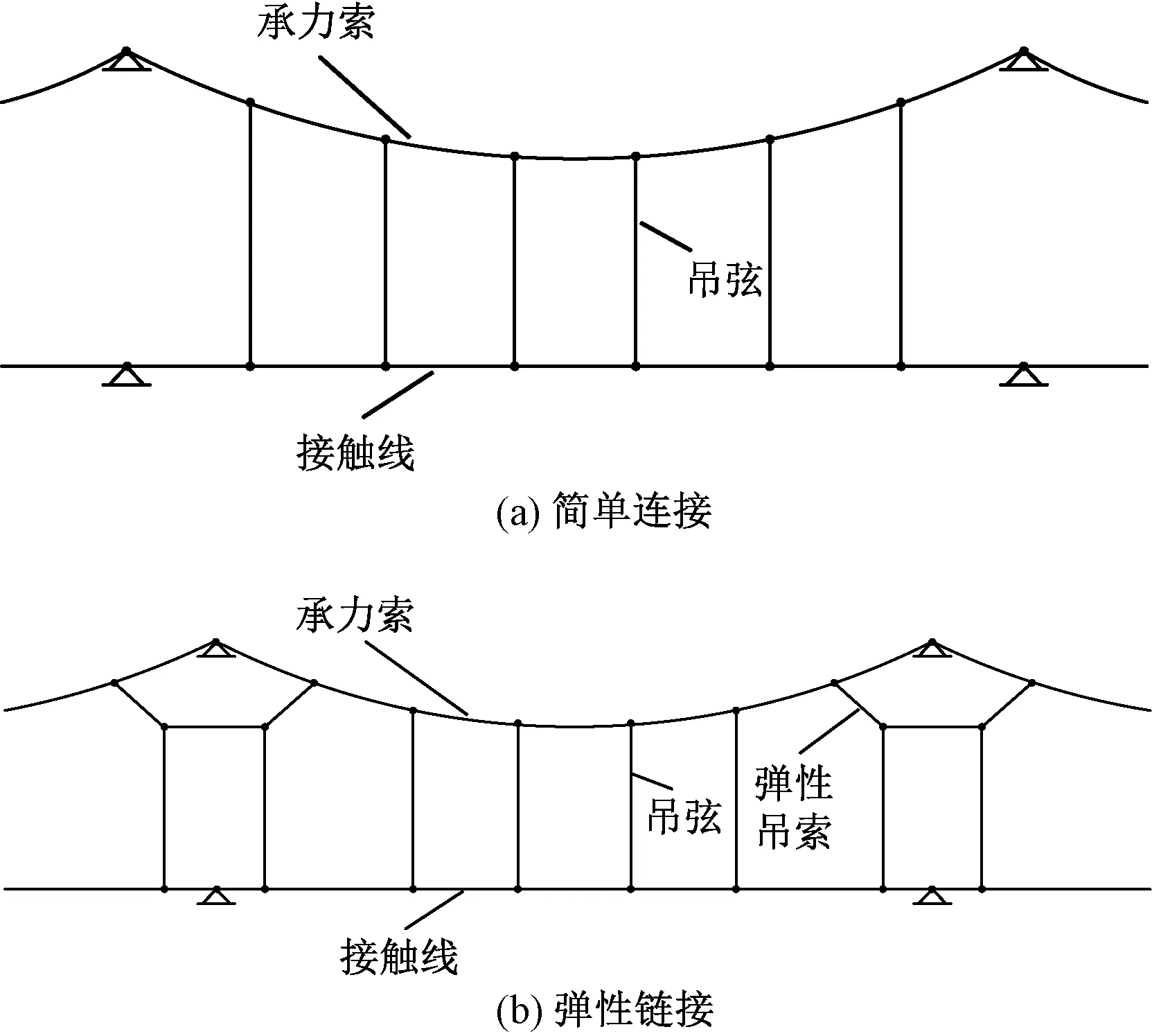
圖2 簡單鏈型、彈性鏈型懸掛接觸網示意

本文將使用基于非線性理論的懸鏈線單元對接觸線、承力索以及彈性吊索進行離散，以吊弦數為nd的單跨彈性鏈型懸掛接觸網為例，將相鄰吊弦間、吊弦與定位點間的承力索、接觸線以及彈性吊索均離散為懸鏈線單元，則對應單元總數N=2(nd+1)+4。

此時考慮左右各2個彈性吊索懸鏈線單元，若計算多跨則應減去重復計算的單元數。而對于簡單鏈型懸掛接觸網，減去彈性吊索的懸鏈線單元數即可。

2.2 接觸網找形流程

本文使用非線性理論對接觸網進行找形，流程見圖3。由于接觸網在鋪架的過程中，吊弦數量以及接觸線的初始構型具有預設條件，即接觸線的各節點坐標參數已知。根據此結構特點，將接觸網離散為懸鏈線單元后，先分離并求解接觸線平衡構型，并計算出各節點的吊弦力；然后整體求解承力索、彈性吊索和吊弦的平衡構型，利用懸鏈線方程式( 8 )初步表示平衡構型下各結構的懸鏈線單元，并確定其中未知參數數量Nx，通過吊弦力平衡關系以及承力索、彈性吊索端部張力平衡關系，建立求解未知參數方程組；最后根據方程組的非線性，使用牛頓-拉夫森法迭代求解。解出未知參數后，進一步可得到初始平衡構型下承力索和彈性吊索各懸鏈線單元解析式，從而完成接觸網找形。

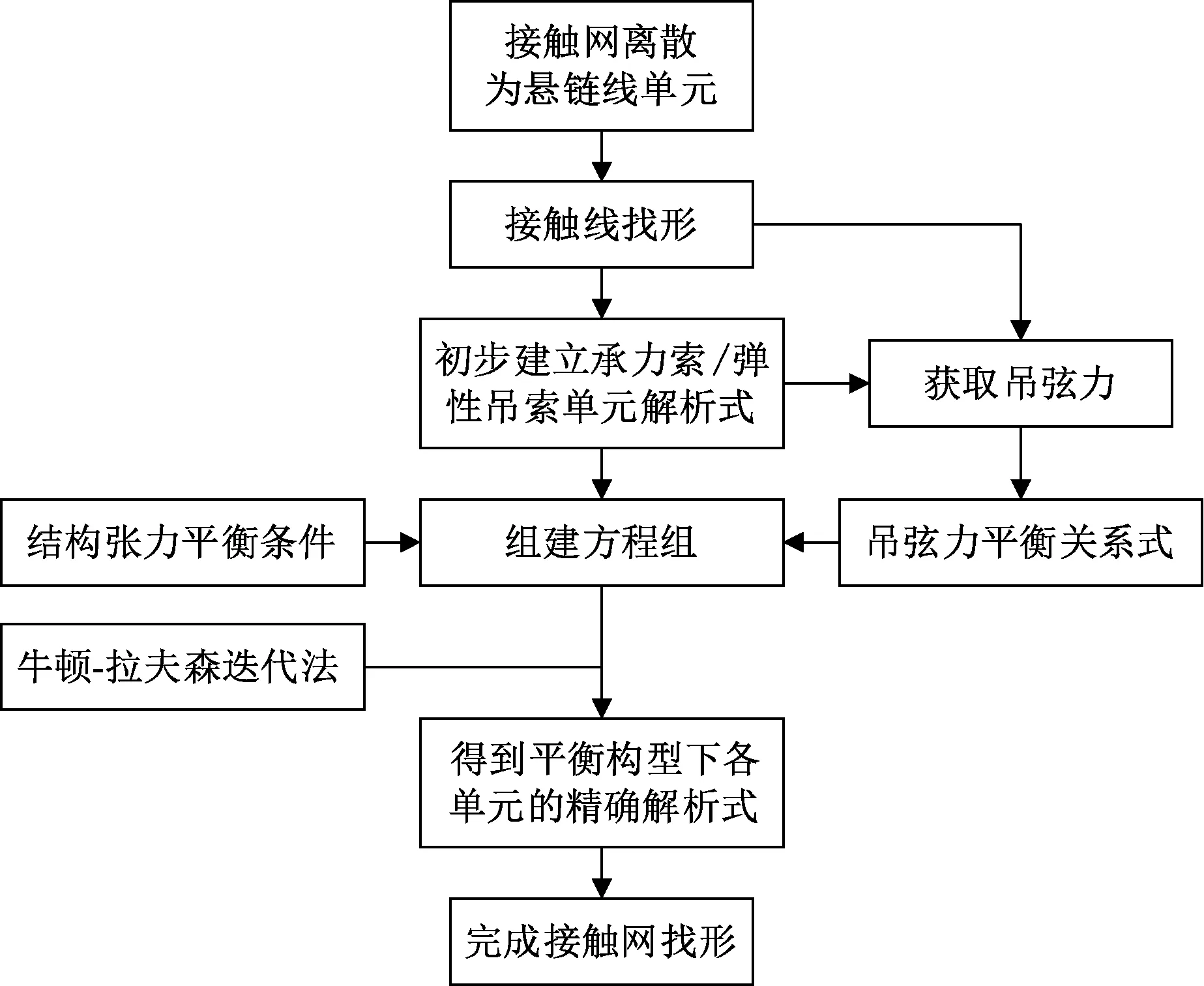
圖3 接觸網找形流程

2.3 接觸網找形理論

以彈性鏈型懸掛接觸網為例進行接觸網找形計算，其主要結構為接觸線、承力索、彈性吊索以及吊弦。含有吊弦數為nd的彈性鏈型懸掛接觸網分析示意圖見圖4，采用下標cw、sw、ms、mw分別表示與接觸線、彈性吊索、彈性吊索上方承力索部分(A′C、DA″段)、承力索中間部分(CD段)的相關參數，如Tcw、Tsw、Tms、Tmw表示接觸線、彈性吊索、彈性吊索上方承力索部分、承力索中間部分的控制張力。需要注意地是，由于存在彈性吊索，一跨內的承力索控制張力不再相等，此時，設計要求的承力索張力Tmw控制在圖4中CD段，而A′C、DA″段的控制張力Tms則需根據力平衡關系求解出。

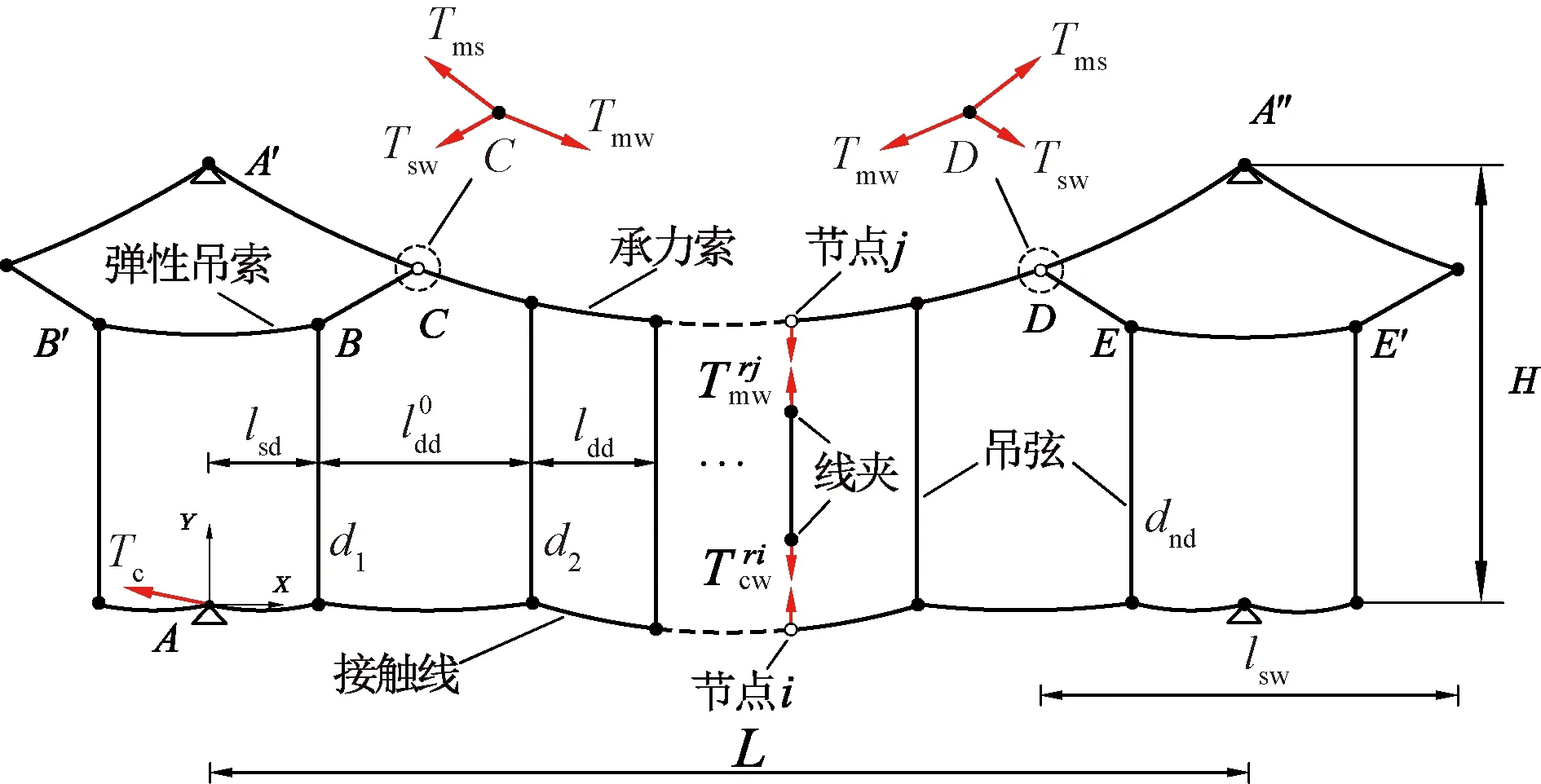
圖4 彈性鏈型懸掛接觸網分析

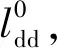
2.3.1 接觸線計算

將接觸網系統離散為懸鏈線單元后，先對接觸線的初始平衡構型進行計算。其中，接觸線的定位點與節點、節點與節點間均離散為懸鏈線單元，由式( 8 )可得各單元方程為

k=0,1,2,…,nd

(10)

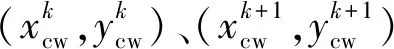
(11)

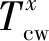
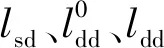
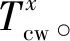
(12)

(13)

表示出接觸線的懸鏈線方程組后即確定了接觸線的初始平衡構型。此時，還需求出接觸線對吊弦的作用力，為承力索、彈性吊索和吊弦的求解做準備。接觸線對第i吊弦作用力可表示為

(14)

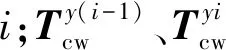
(15)

2.3.2 承力索、彈性吊索與吊弦整體計算

彈性吊索上方承力索部分(A′C、DA″段)、承力索中間部分(CD段)、彈性吊索的控制張力不同，但每部分的水平張力為恒定值，可以分別對其建立懸鏈線單元方程。彈性吊索的B′B、EE′對應的懸鏈線單元分布在兩跨之間，在對單跨模型找形時將其考慮在內，即單跨模型考慮左右各2個彈性吊索懸鏈線單元。

通過式( 8 )分別建立承力索、彈性吊索的懸鏈線單元方程為

k=1,2,…,nd-1

(16)

k=0,nd

(17)

n=1,2,4,5

(18)

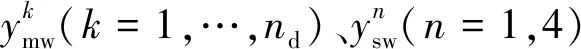
同時，Cmw、Cms以及Csw可表示為

(19)

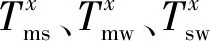
連接承力索和接觸線的nd-2個吊弦力平衡方程、連接彈性吊索和接觸線的2個吊弦力平衡方程分別為

i=jj=2,…,nd-1

(20)

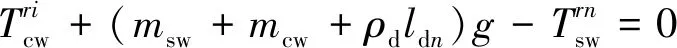
i=1,ndn=1,4

(21)

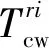
(22)

(23)

式(20)可由式(14)求得，表達式為

(24)

(25)

式(21)中其求解形式與式(14)、式(24)一致，即

(26)

其中

(27)

接著，建立承力索以及吊弦端部張力平衡方程為

(28)

(29)

(30)

以上已建立方程數為nd+3，還需補充3個方程才能求解。承力索單元A′C的端部張力Tms未知，點C為連接三部分的節點，對點C建立力平衡方程可得

(31)

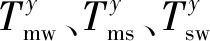
(32)

注意到節點D也為承力索與彈性吊索的連接點，建立節點D垂向力平衡方程為

(33)

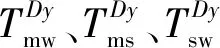
聯合式(20)～式(33)可以建立含有Nx個方程的非線性方程組，采用牛頓-拉夫森法對該非線性方程組進行求解，可將其未知數全部求解出，即將承力索與彈性吊索的初始平衡構型以及吊弦長度求解出。至此，彈性鏈型懸掛接觸網的找形計算全部完成。

對于簡單鏈型懸掛接觸網，見圖2，承力索的定位點下方未設有彈性吊索。此時，Tms=Tmw，即整根承力索控制張力為恒定值，同樣可以通過上述彈性鏈型懸掛接觸網找形計算過程完成接觸網找形。

2.3.3 迭代算法

由于牛頓-拉夫森迭代法具有收斂的快速性和準確性等優點[22]，本文將使用該方法對2.3.2節組建的非線性方程組進行求解，求解流程見圖5。

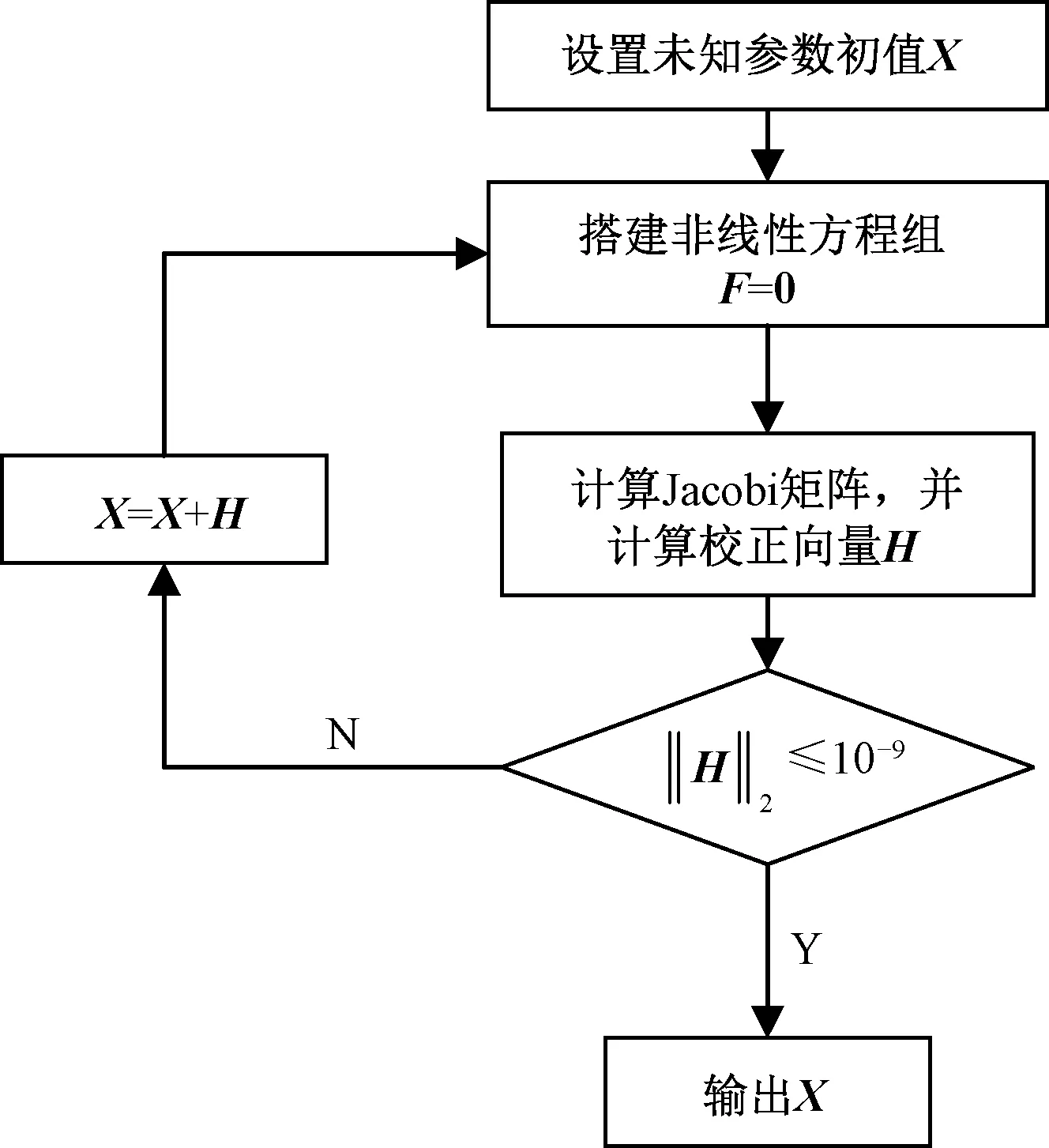
圖5 非線性方程組求解流程

設置未知參數的迭代初值，組成初值矩陣X；將對應初值代入各方程中組建非線性方程組F=0；計算出Jacobi矩陣J，并由H=-J-1F得出校正矩陣H；判斷校正矩陣H的二范數是否滿足預設條件，若不滿足，則使用校正后矩陣X=X+H再次計算，若滿足，則輸出矩陣X。此時，輸出的X為未知參數的數值解，將其代入式(16)～式(18)中可將承力索、彈性吊索以及吊弦的平衡構型表示出，即完成接觸網的找形。

3 模型驗證

上述方法將用于不同接觸網模型的找形，確定模型的初始平衡構型。接觸網的找形結果可通過吊弦的長度以及接觸線的平衡構型來評估[23]，因此，將算例相關計算結果與標準或已發表文獻中相同邊界條件的模型結果進行對比，用于驗證本文找形方法的準確性、有效性和工程實用性。

3.1 簡單鏈型懸掛接觸網模型

模型1選擇歐洲標準EN 50318—2018中簡單鏈型懸掛接觸網的參考模型[23]，該模型參數用于檢查接觸網的新生產線是否合格，也可用于對仿真模型的初步檢查。文獻[3]中將該模型用于現有10家機構開發使用的不同模擬軟件找形結果對比。該接觸網模型的幾何參數見表1，該接觸網模型的物理參數見表2。

表1 模型1接觸網幾何參數

表2 模型1接觸網物理參數

本文方法得到的模型1接觸網模型初始平衡構型見圖6。將計算所得吊弦長度與標準對比，結果見表3，由于該模型具有對稱性，只將前5吊弦進行對比，由表3可知，吊弦長度結果與標準值非常接近，最大相對誤差為0.34%，說明了本文找形方法的準確性。

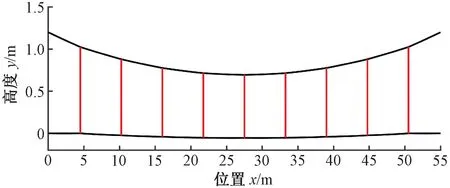
圖6 簡單鏈型懸掛接觸網模型初始平衡構型

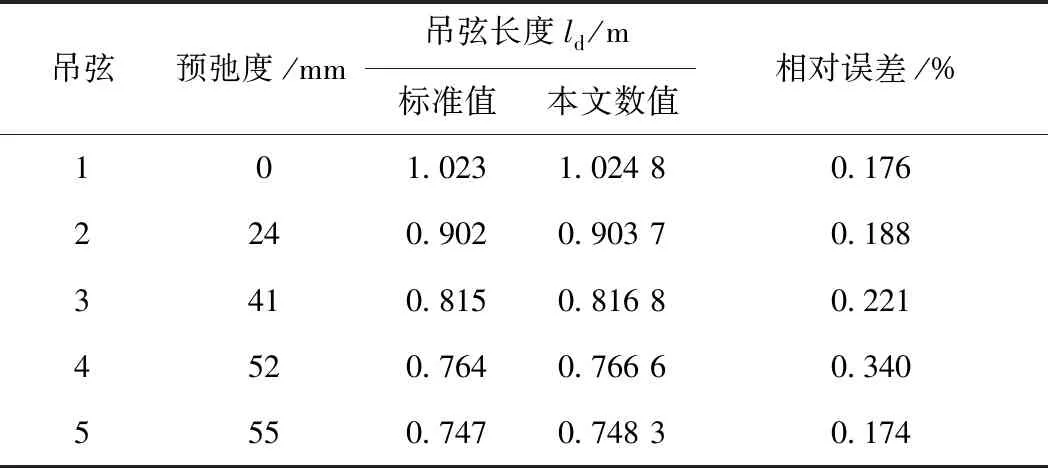
表3 吊弦長度計算結果對比

同時，對找形結果中接觸線初始構型進行評估。文獻[3]中各家機構由于邊界條件考慮不一致，其所得的接觸線初始構型雖存在差異，但結果基本一致。將本文找形方法所求構型與其中一家機構PACDIN[24]的計算結果進行對比，見圖7。將吊弦力與該機構計算結果進行對比，見表4，雖然結果存在一定差異，但最大相對誤差為1.720%，未超過2%，可認為利用本文方法找形結果正確，且準確性好。

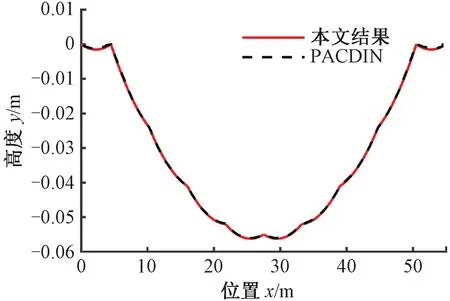
圖7 接觸線初始構型對比

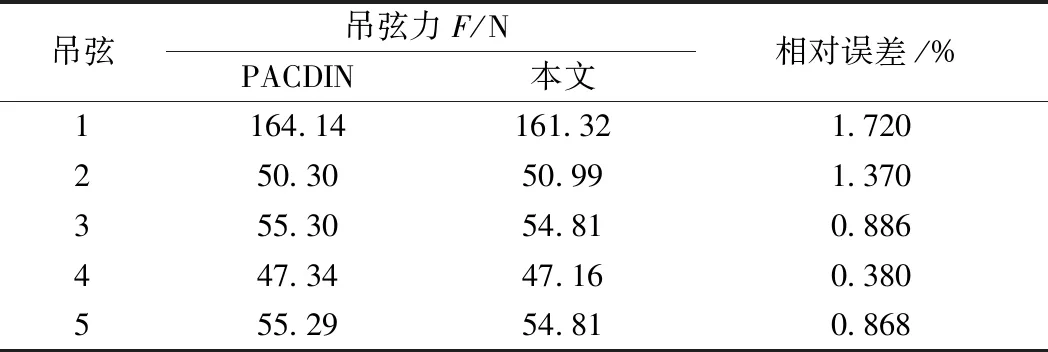
表4 吊弦力計算結果對比

3.2 京津城際鐵路接觸網模型

模型2實際設計京津城際鐵路接觸網模型，文獻[17]根據京津線設計要求通過拋物線找形法完成標準跨距接觸網的找形，本文將使用文獻中相關參數進行找形計算，驗證本文計算方法的精確性。模型2的幾何參數見表5，物理參數見表6。

表5 模型2接觸網幾何參數

表6 模型2接觸網物理參數

京津線接觸網單跨模型找形結果見圖8，提取吊弦長度以及吊弦力等相關參數與文獻[17]參考值進行對比，見表7。

圖8 京津城際鐵路接觸網模型初始平衡構型

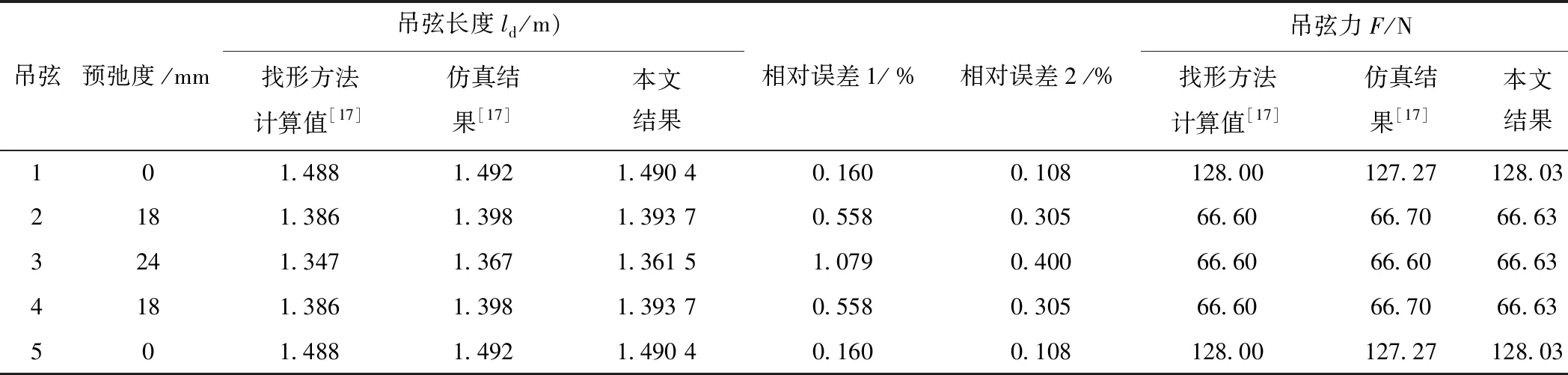
表7 吊弦長度及吊弦力計算結果對比

從表7中可以看出，在吊弦力計算方面，本文計算結果與文獻[17]的計算值、仿真值基本一致；而在吊弦長度上，本文計算結果較文獻[17]的計算值更接近于其仿真值，最大相對誤差僅為0.4%，即本文方法較拋物線找形法能夠更精準地計算接觸網模型吊弦長度。

3.3 彈性鏈型懸掛接觸網模型

模型3選擇標準EN 50318—2018中彈性鏈型懸掛接觸網的實測線路模型[23]，對該接觸網模型中錨段關節進行找形，與前幾個算例不同地是，本算例接觸網模型帶有坡度，且含有彈性鏈型懸掛接觸網、過渡跨以及簡單鏈型懸掛接觸網等常用接觸網模型，具有代表性。該接觸網模型的幾何參數見表8，該接觸網模型的物理參數見表9。

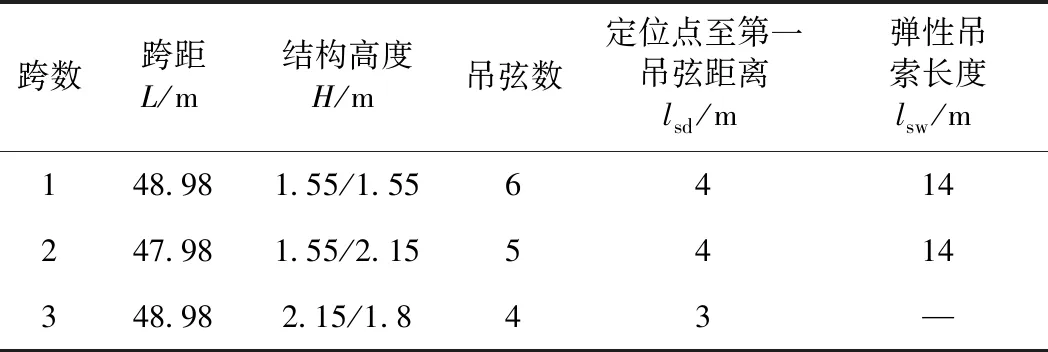
表8 模型3接觸網幾何參數

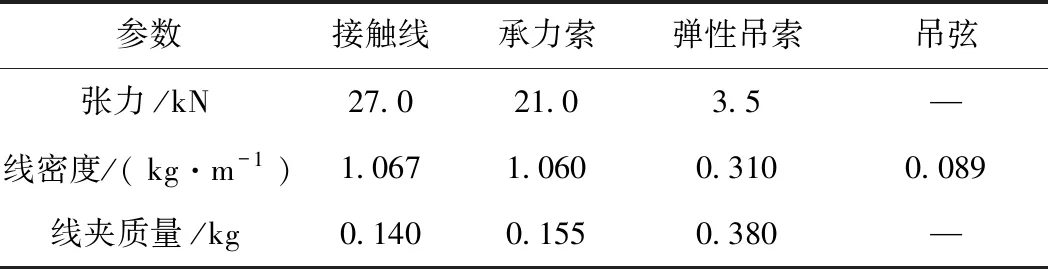
表9 模型3接觸網物理參數

通過本文方法對接觸網模型3進行找形，所得到的接觸網初始平衡構型見圖9。由于本模型第一跨為無預弛度的彈性鏈型懸掛接觸網，第二跨(錨段關節過渡跨)中，左側含有彈性吊索而右側為簡單鏈型，且整垮具有一定坡度，涵蓋了現有接觸網不同結構、邊界條件。因此，提取第一、二跨吊弦長度計算結果與標準EN 50318—2018中實測數據對比，其結果見表10、表11。

圖9 接觸網錨段關節處初始平衡構型

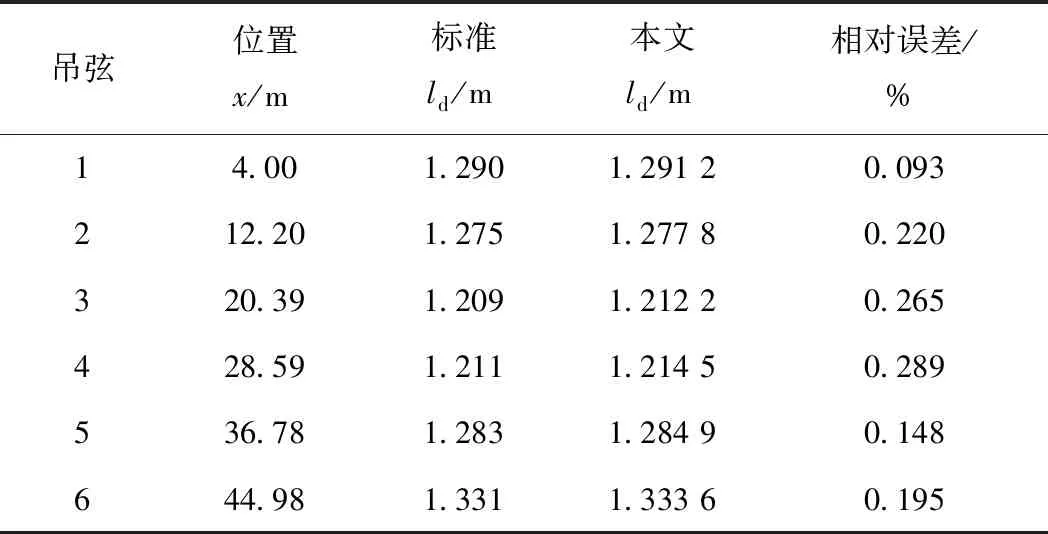
表10 模型3第一跨吊弦長度計算結果對比

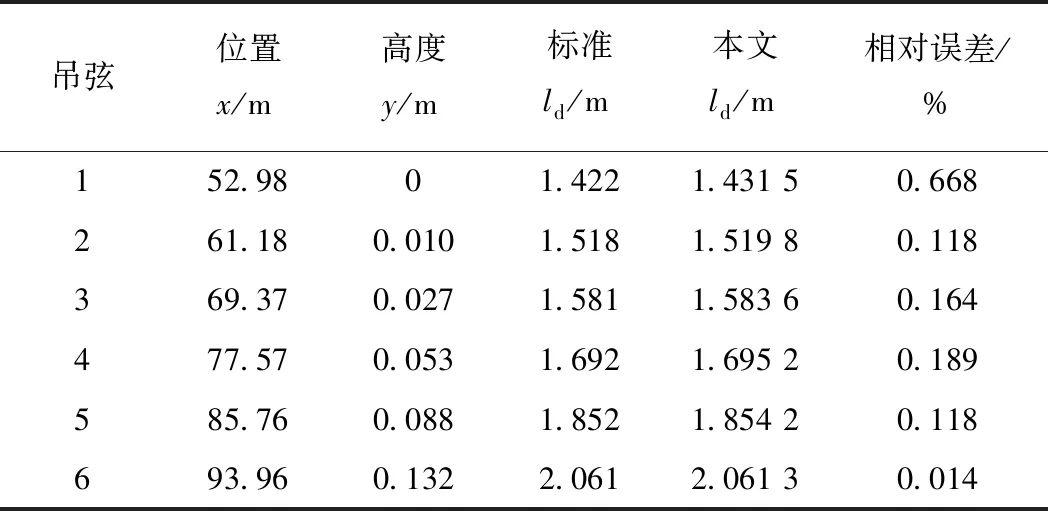
表11 模型3第二跨吊弦長度計算結果對比

通過以上對比可知，本文計算結果與標準實測值非常接近，最大相對誤差僅為0.668%，說明了本文方法找形結果準確性好，且證明了方法的工程實用性。

4 結論

本文進行了一種基于非線性理論的接觸網找形方法研究，并以彈性鏈型懸掛接觸網為例建立了接觸網求解模型。將接觸網相鄰吊弦間、吊弦與定位點間的承力索、接觸線以及彈性吊索均離散為基于非線性理論的懸鏈線單元后，先分離求解接觸線初始構型；再通過力平衡關系搭建用于求解承力索、彈性吊索以及吊弦平衡構型的非線性方程組，其中包括吊弦力平衡關系以及結構控制張力平衡關系；最后使用牛頓-拉夫森迭代法求解，得到接觸網初始平衡構型，從而完成找形。通過三個算例驗證，得出以下結論：

(1)接觸網找形過程的求解規模取決于吊弦數量與控制張力數量，求解規模相對較小，并能快速求解。

(2)對歐洲標準EN 50318—2018中簡單鏈型懸掛接觸網的參考模型進行找形計算，結果對比表明，吊弦長度的計算結果與標準值對比，最大僅相差0.34%。接觸線初始平衡構型與某機構找形結果具有良好的一致性，所得吊弦力與其最大相差1.720%，滿足工程應用要求，證明了本文找形方法的準確性和有效性。

(3)對京津城際鐵路接觸網標準跨進行找形計算，結果與文獻結果對比顯示，吊弦力計算基本一致，而吊弦長度計算更接近文獻仿真計算值，驗證了本文找形方法的精確性。

(4)對歐洲標準EN 50318—2018中彈性鏈型懸掛接觸網的實測線路模型進行找形計算，結果對比顯示，吊弦長度的計算結果與標準值對比，最大僅相差0.668%，驗證了本文找形方法的工程實用性。

(5)已實現對簡單鏈型、彈性鏈型、錨段關節等接觸網模型找形，也適用于其他類型、不同邊界條件的接觸網找形。同時，找形結果可作為初始條件用于受電弓與接觸網的動態仿真計算，也可為實際線路的接觸網設計提供參考。