一道質檢試題的多視角求解

王 波

(湖北省松滋市第一中學 434200)

近幾年來，與圓錐曲線有關的四點共圓問題一直備受高考命題人的青睞.這類問題往往設置巧妙、解法多樣、內涵豐富,題目難度較大.本文以2022年湖南省株洲市一道質檢試題的多角度思考為例,與大家共同體驗數學問題的求解奧秘.

一、試題呈現

二、解法探究

視角1利用圓中角的性質

解法1如圖1,連結MF,由于M,F分別為OB,AB的中點,則MF∥OA,得∠AOM+∠OMF=π.又O,A,F,M四點共圓,有∠OAF+∠OMF=π,所以∠AOM=∠OAF.

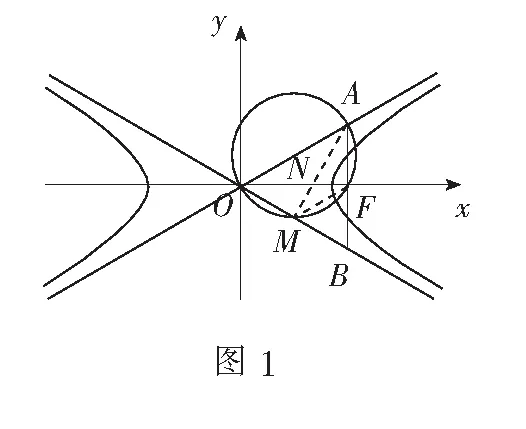
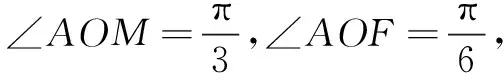
解法2如圖1,由O,A,F,M四點共圓,得∠OAF+∠OMF=π.又∠OMF+∠BMF=π,所以∠OAF=∠BMF.

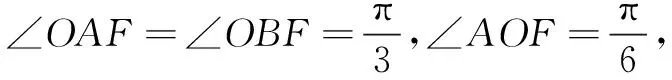
評注解法1與解法2均運用了圓內接四邊形對角互補這一性質,推導出三角形?AOB為正三角形,由此可得出雙曲線漸近線的傾斜角,最終順利求得離心率.這兩種解法都很好地體現了圖形本身具備的幾何特性這一本質特征.

視角2利用圓冪定理

解法3如圖1,由O,A,F,M四點共圓,應用割線定理得|BF||BA|=|BM||BO|.

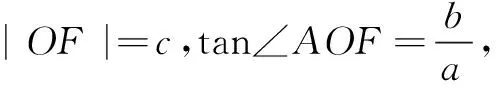
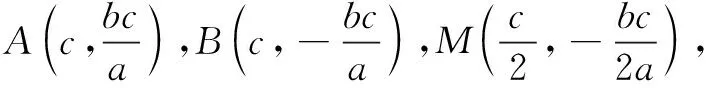
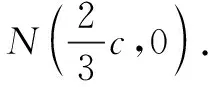
評注對于四點共圓這一條件,除了轉化為圓中角的關系,我們還可以研究圓中的線與弦.解法3將四點共圓轉化為割線定理,運用線段乘積來得到a,b關系,最終得出離心率;解法4運用相交弦定理得出到a,b關系求離心率,二者具有異曲同工之妙.

視角3利用圓的方程與圓心坐標

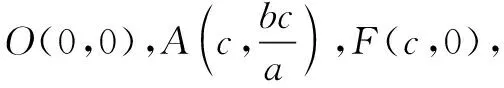
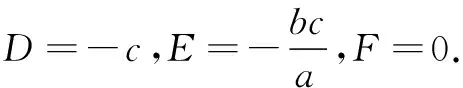
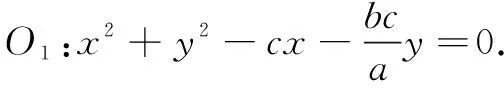
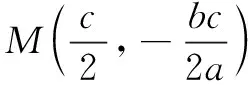
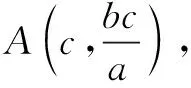
評注解法5先設出圓的方程,再由圓上三點坐標確定參數,代入第四點即可得出a,b關系.解法6的巧妙之處是根據幾何特征找到了圓心,然后運用距離公式進行翻譯,最終得出離心率.這兩種解法體現了代數法在幾何中的應用.

通過以上幾種解法可以發現：本題看似復雜,實則簡單易解.解……