外力作用下板塊模型運動的臨界問題分析

趙清鋒

（武漢市卓刀泉中學建和分校，湖北 武漢 430065）

板塊模型是物理學中的基本模型.木板與物塊的運動情況受其質量、板塊之間動摩擦因數、木板與地面之間動摩擦因數、外力的作用對象、外力大小、外力方向等多個因素的影響.條件不同，板塊運動狀態不同，給出不同條件運動狀態結果不同.這也是中學物理常考的重點內容.相關文獻多研究水平外力作用在物塊或木板上從而分析板塊運動情況，［1-5］本文從不同外力沿不同方向的角度對板塊模型運動的臨界問題進行詳細討論，為相關研究提供思路.

1 基本模型及物塊和木板運動的臨界條件

水平地面上有一質量為m1的長木板，木板的左端上有一質量為m2的物塊，用與水平方向成θ角的拉力F 作用在物塊上，考慮外力F 不同，物塊和木板的運動狀態不同，設F 隨時間t 變化關系為F=k·t（k為常量）.木板與地面間的動摩擦因數為μ1，物塊與木板間的動摩擦因數為μ2.假設最大靜摩擦力均與相應的滑動摩擦力相等，重力加速度大小為g，如圖1所示.

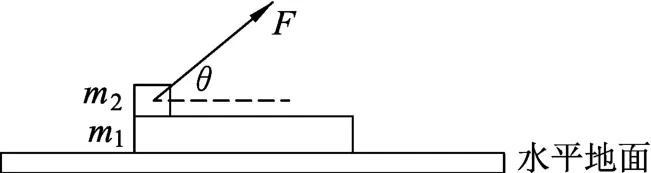
圖1 板塊模型

當外力很小時，物塊和木板均不運動，隨著外力F 增大到一定程度，物塊開始運動，而此時的運動情況可能出現兩種情況：（1）物塊運動，木板靜止；（2）物塊和木板一起向右運動.對m2和m1分別進行受力分析如圖2、圖3所示.其中F12為木板對物塊的支持力，f12為木板對物塊的摩擦力，F21為物塊對木板的壓力，f21物塊對木板的摩擦力，F地為地面對木板的支持力，f地為地面對木板的摩擦力，m1g和m2g分別為木板和物塊所受的重力.

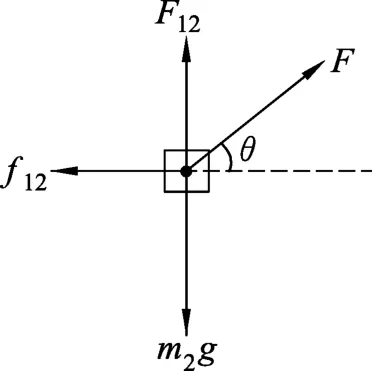
圖2 對物塊m2進行受力分析

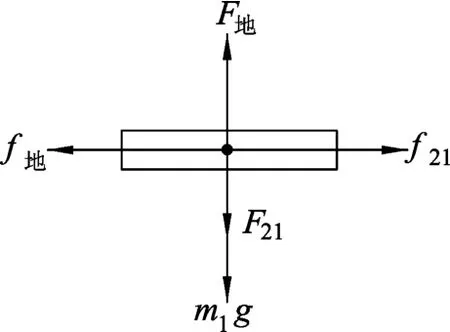
圖3 對木板m 1進行受力分析

隨著拉力F 增加，物塊與木板之間最大靜摩擦力f12m和木板與地面之間對應的最大靜摩擦力f地m也隨之變化，即

從（1）（2）兩式均可以看出，f12m和f地m均為拉力F 的一次函數，隨著F 的變化，當f12m和f地m相等，且等于拉力F 在水平方向的分力F cosθ時，此時達到物塊與木板之間、木板與地面之間剛要運動的臨界條件，令f12m=F cosθ，此時可得

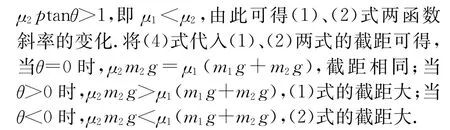
根據以上分析，取m1=2 kg、m2=1 kg、μ2=0.5、g=10 m／s2，μ1滿足（4）式，分別取θ=30°、θ=-30°、θ=0°，數值計算并作圖分析.圖4（a）（b）（c）為f12m、f地m、F cosθ隨F 的變化關系圖像.從圖中可以看出，當μ1滿足（4）式時，與上文分析一致.

圖4 θ取不同值時，f 12m、f地m、F cosθ隨F 的變化關系

當F 滿足（3）式時，對應的臨界力F cosθ隨θ的變化關系如圖5所示.

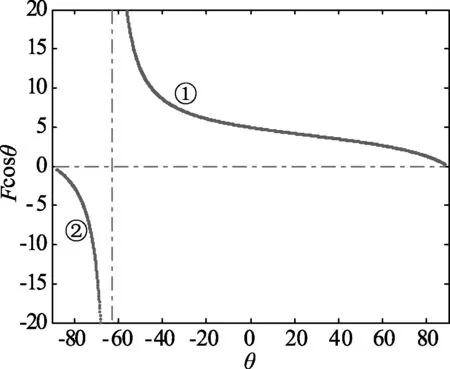
圖5 F cosθ隨θ 變化關系

2 θ＞0，物塊和木板運動的情況分析

2.1 物塊運動，木板靜止

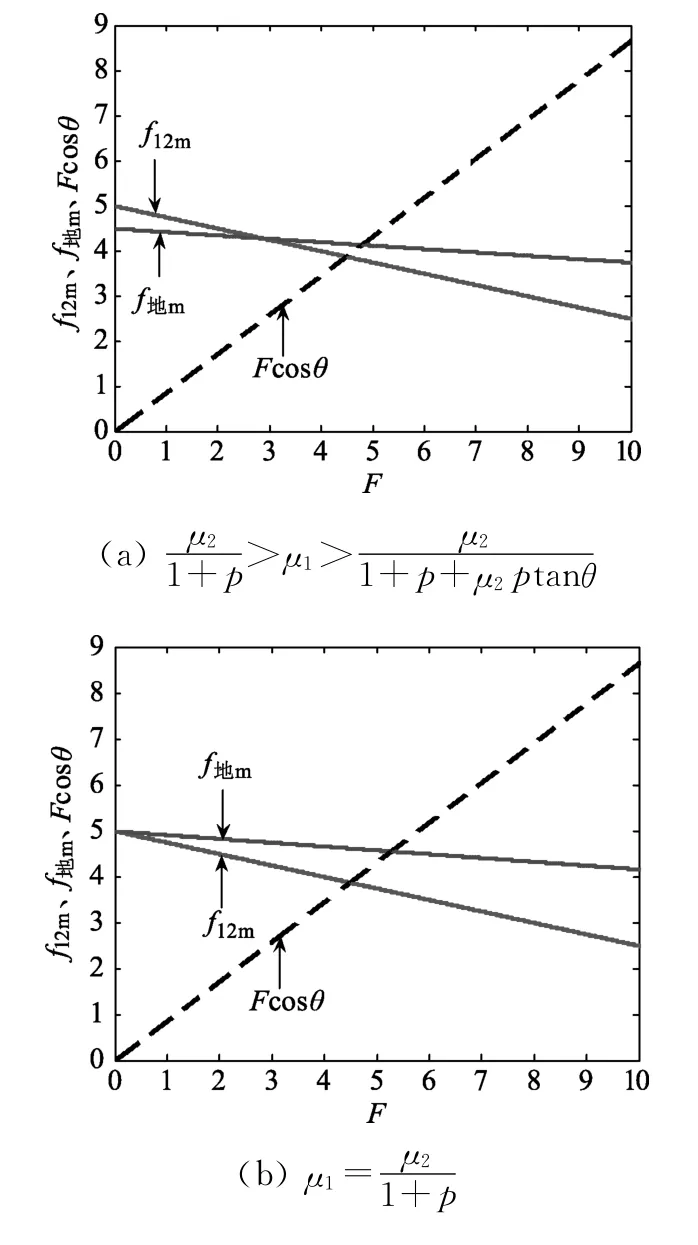
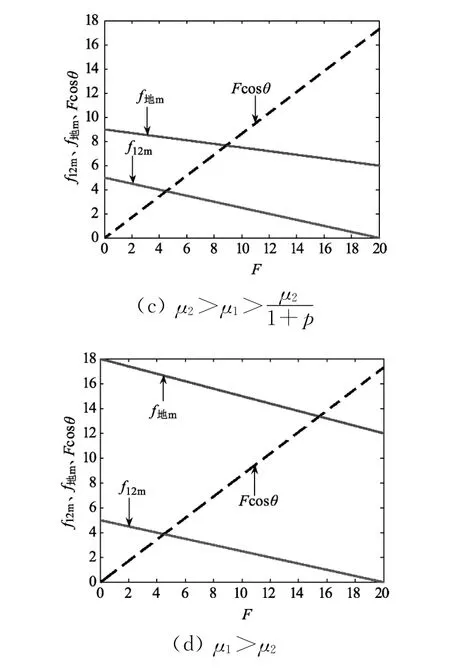
圖6 f 12m、f地m、F cosθ隨拉力F 的變化關系

圖6（a）-（d）中μ1取值分別為μ1=0.15，μ1=0.1667，μ1=0.3，μ1=0.6.圖像分析結果與上文討論結果一致，且θ＞0時，若開始木板未動，則一直滿足f12m＜f地m，即木板將一直不動.數值計算結果可得，當拉力F=4.480 N 時，物塊開始做加速度增加的加速運動，直到物塊脫離木板，如圖7所示.

圖7 加速度a隨F 的變化關系

2.2 物塊和木板先一起向右運動，再相對運動

根據上述數值計算結果得到F1=3.2750 N、F2=4.9341 N、F3=10 N、F4=15.8370 N、F5=20 N.當拉力F≤F1時，物塊和木板均處于靜止狀態；當拉力F1＜F≤F2時，物塊和木板一起做加速度增加的加速運動，在拉力F=F2時，木板加速度達到最大，為a2max=0.5066 m／s2；當F＞F2時，物塊和木板相對運動，物塊做加速度增加的加速運動，直到F=F5時，物塊離開木板不再水平運動，而木板先做加速度減小的加速運動，當F=F3時，木板的加速度減小為0，然后繼續減速運動，當拉力F=F4時，木板速度減小為0，加速度達到最小a4min=-0.5837 m／s2，之后靜止不動.

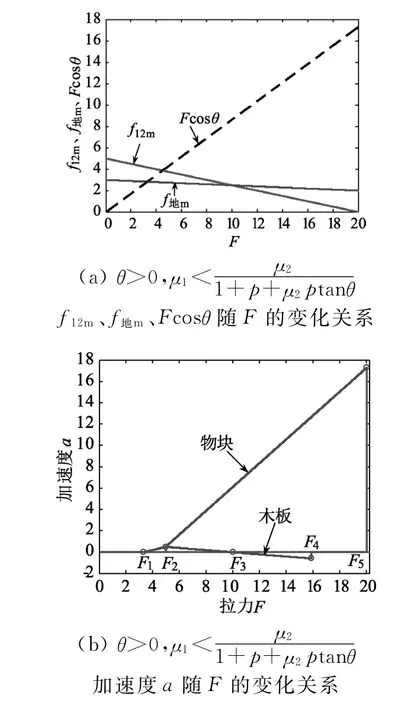
圖8

本文討論的拉力F 隨時間t 均勻變化，若拉力為某一固定值，對物塊的運動的加速度沒有影響，僅僅是拉力F≥F3時，木板由于沒有初始速度而不再減速，處于靜止不動.對于拉力F 為其他函數，也可以用類似的方法進行分析.

3 θ＜0，物塊和木板運動的情況分析

3.1 物塊運動，木板靜止

按照上圖取值，通過數值計算發現，當拉力F=8.1165 N 時F·cosθ=f12m，物塊開始運動.當F=F6=40 N 時f12m=f地m，木板開始運動，此時根據圖形分析可得，物塊與木板均做加速度增加的加速運動，物塊加速度增加得更快.

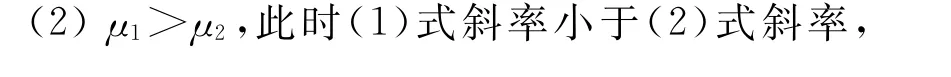
從數值計算結果及圖像分析可得，當μ1＞μ2時，圖10（b）中物塊加速度變化與圖9（b）中一樣，只是木板此時處于靜止狀態.

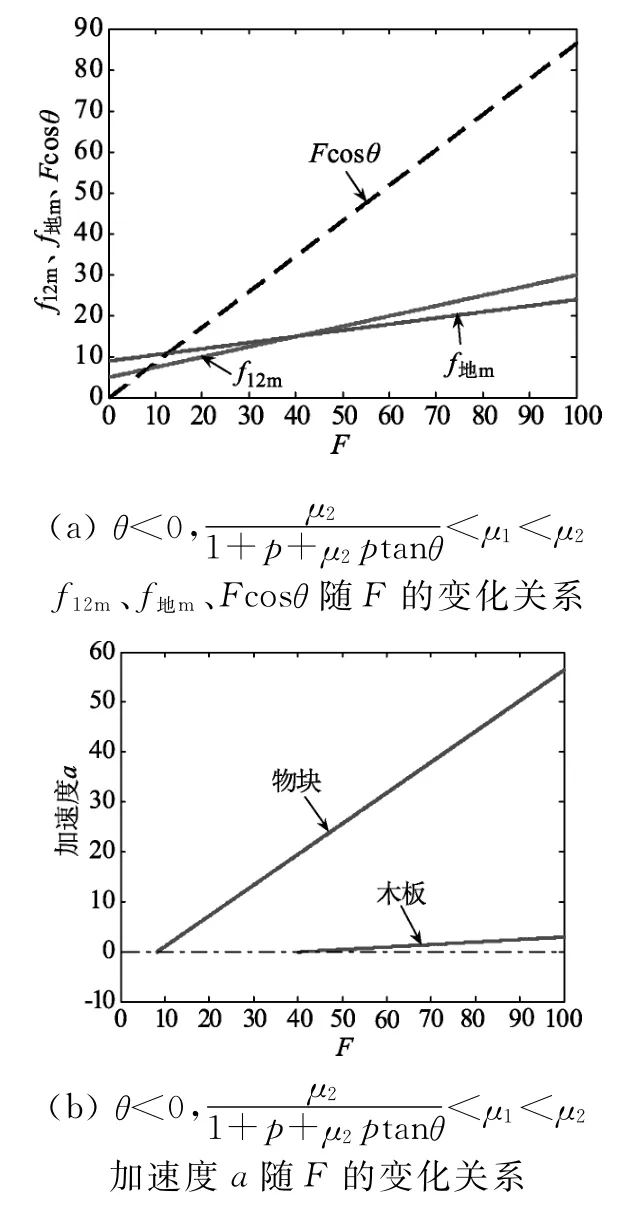
圖9

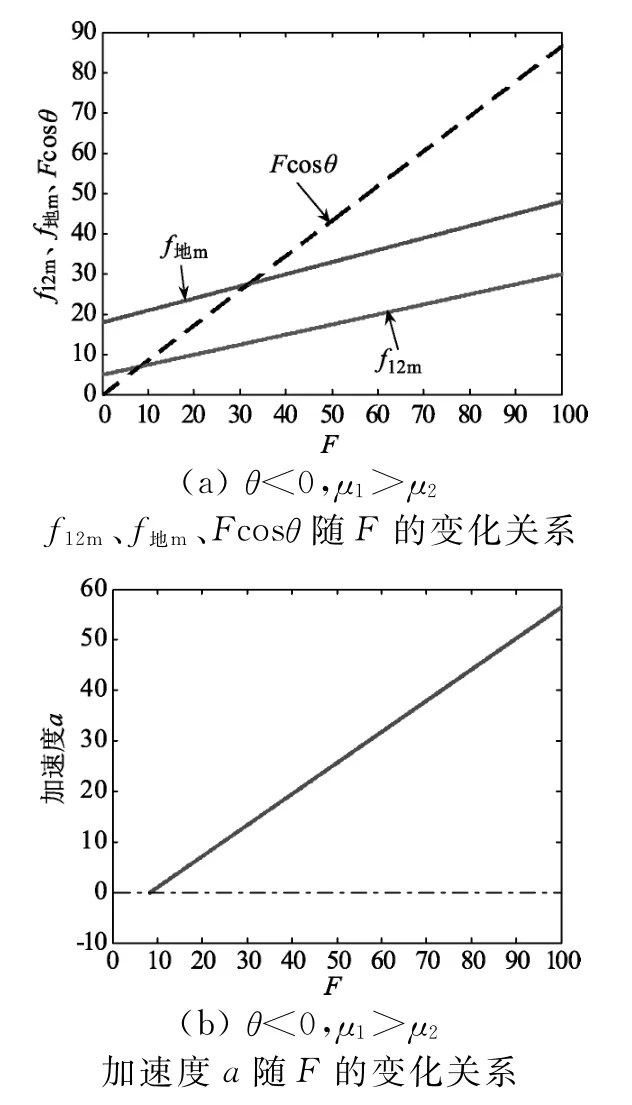
圖10

3.2 物塊和木板先一起向右運動，再相對運動

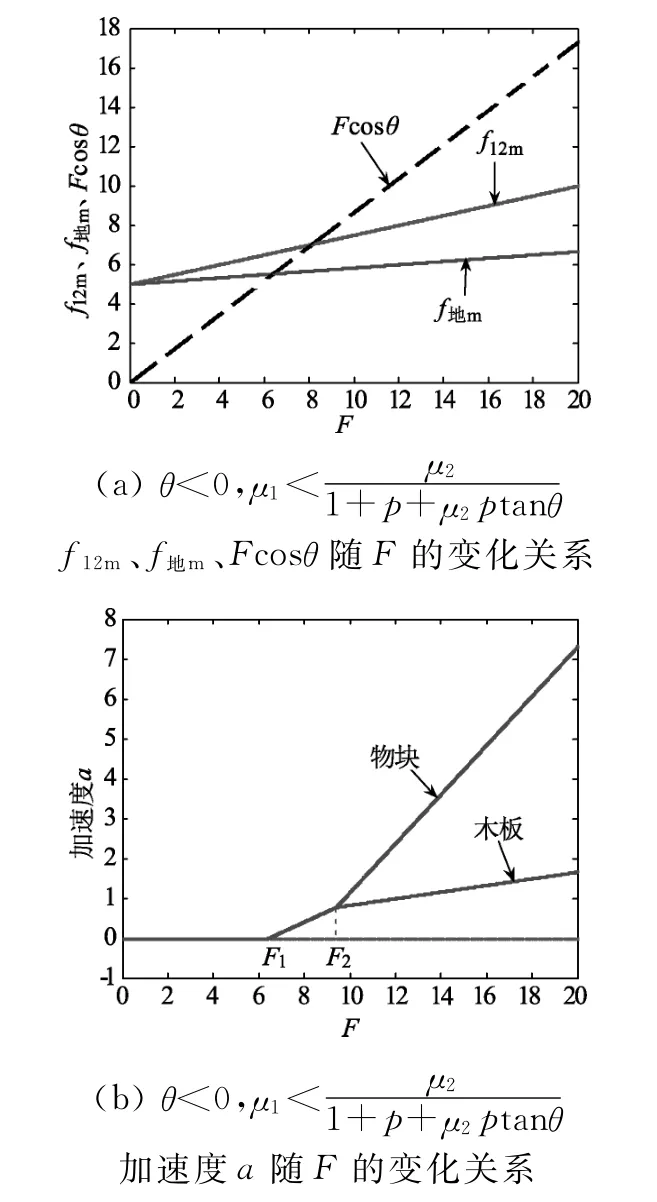
圖11

根據上述數值計算結果得到，F1=6.3883 N、F2=9.3863 N.當拉力F≤F1時，物塊和木板均處于靜止狀態；當拉力F1＜F≤F2時，物塊和木板一起做加速度增加的加速運動；當F＞F2時，物塊和木板相對運動，且均做加速度增加的加速運動，物塊加速度增加得更快.