用洛必達法則求解高中函數問題的合理轉換方法

包文濤

(福建省南平第一中學)

函數是高中數學的重要知識點,“由不等式恒成立求解參數范圍”又是函數的熱點問題,這類問題在實際求解中,大部分是通過對整體進行含參討論,進而求解參數范圍.在實際教學中,筆者發現,有部分學生無法掌握含參討論的方法.如果對該問題進行參變分離求解函數確界,會出現“0比0”這類高中生無法求解的情況.于是,筆者提出了兩種方法,引導學生在高中的知識體系下合理應用高等數學中的洛必達法則解決問題.

1 題型舉例

例1 設函數f(x)＝x(ex－1)－ax2.若當x＞0時,f(x)≥0恒成立,求實數a的取值范圍.

2 參考答案的求解過程

f(x)＝x(ex－1)－ax2＝x(ex－1－ax).

令g(x)＝ex－1－ax,則g′(x)＝ex－a.

若a≤1,則當x∈(0,＋∞)時,g′(x)＞0,g(x)為增函數,而g(0)＝0,從而當x≥0時,g(x)≥0,即f(x)≥0.

若a＞1,則當x∈(0,lna)時,g′(x)＜0,g(x)為減函數,而g(0)＝0,則當x∈(0,lna)時,g(x)＜0,即f(x)＜0.

綜上,a的取值范圍是(－∞,1].

3 參變分離求解的情形分析

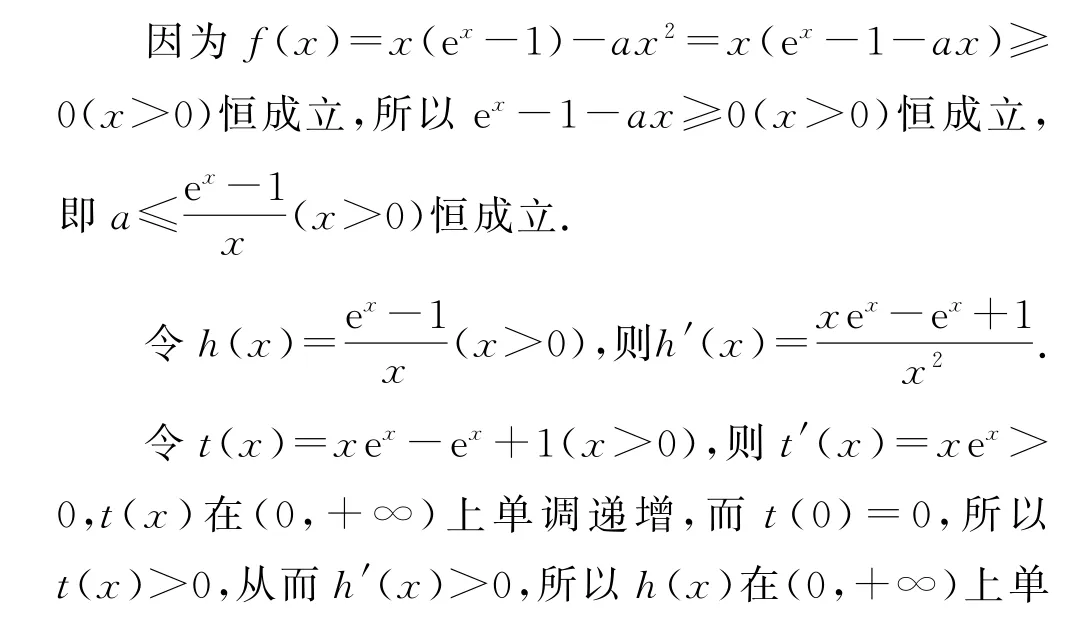
4 高等數學中的洛必達法則進一步求解

5 在高中知識體系下的轉換方法

5.1 在高中知識體系下轉換方法1

在高中數學導數這一章中,第一節就介紹了極限的概念,并由此引出導數.因此,雖然此類題型在高中生的視角下無法直接使用洛必達法則求解,但可以通過極限,將其轉換為導數的定義,進而繞過洛必達法則,解決此類題型,具體過程如下.

5.2 在高中知識體系下的轉換方法2

筆者在實際教學中發現,對于基礎薄弱的學生來說,導數的定義相對較為陌生,并不能很好地應用方法1進行求解.針對此類學生,筆者提出了方法2,供其參考.方法2的思路在于“先猜后證”.

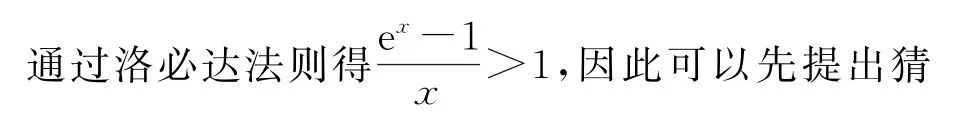
6 應用舉例

7 小結

在解決該類問題的傳統方法中,含參討論是解題的難點.本文采用兩種方法,使得該類問題能夠通過參變分離進行解決.

方法2通過“先猜后證”的形式,求出參變分離后新函數的確界,進而解決該類問題.實踐表明,這種處理方式,更適合基礎薄弱的學生.

兩種方法都能將高等數學中的洛必達法則延伸到高中數學中使用.在平時的學習中,學生可以在標準答案外,擴展、延伸這兩種方法,依據自身理解,在具體解題中選擇適合自己的方法.