k-means 聚類分析算法在人工智能+個性化學習系統中的應用

浦慧忠

（無錫城市職業技術學院，江蘇 無錫 214153）

0 引言

通常情況下，人們在逛電商網站時都會收到一些推銷活動的通知，但該客戶之前并沒有關注過那些商品。那么，這些電商網站是依據什么決定給客戶推銷該商品的呢？究其原因就在于電商網站會根據用戶的年齡、性別、地址以及歷史數據等等信息，將其分為：“年輕白領”、“一家三口”、“家有一老”、”初得子女“等類型，在此基礎上就會根據用戶的特征類型，向其推送不同的優惠活動。研究中，利用這些數據將用戶分為不同的類別時，就會用到聚類分析。

研究可知，聚類就是將一個數據集劃分為若干組或類的過程。通過對數據進行分組（目的），若組內的相似性越大、組間的差距越大，聚類效果就越好（評價標準）。而聚類分析就是致力于發現這些數據對象之間的關系，期寄在相似的基礎上收集數據來分類。聚類大多是應用在數據挖掘、數據分析領域，并屬于機器學習中非監督學習的范疇。目前，已經比較成功地解決了低維數據的聚類問題。但由于實際應用中存在數據的復雜性，特別是面對高維數據和大型數據的情況下，現有算法的性能則亟待改進。

隨著技術的進步，數據收集越來越容易，導致數據庫規模越來越大、復雜性越來越高，其維度（屬性）通常可以達到成百上千維，甚至更高。因此，許多在低維數據空間表現良好的聚類方法往往在高維空間上無法獲得好的效果（圖1 為二維和三維空間下的聚類結果對比）。聚類效果的好壞主要取決于2 個因素：一是衡量距離的方法（distance measurement），二是聚類算法（algorithm）的選擇。聚類分析的核心是選擇合適的聚類算法，目前許多聚類算法在小于200 個數據對象的情況下成效明顯，但對于一個大規模數據庫，將導致結果有很大的偏差。因此，亟需研發出一個具有高度可伸縮性的聚類算法。迄今為止，高維聚類分析已成為一個重要研究方向，同時也是聚類技術的難點。

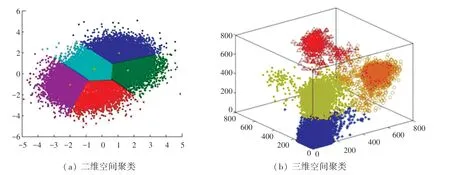
圖1 二維、三維空間下的聚類Fig.1 Clustering in two-dimensional and three-dimensional spaces

1 k-means 算法

通過研究經典和常用的聚類方法，并分析比較各自的優缺點后可以發現：k-means 算法不僅容易理解，而且也容易用代碼實現。k-means 算法采用基于劃分的方法，簡單易行、效率高，現已廣泛應用于大規模數據的聚類分析中，目前絕大多數聚類分析的研究均圍繞著該算法進行擴展和改進。

1.1 算法原理

k-means 中的是指簇的個數，需預先指定。迭代時選擇簇內樣本的均值向量作為簇的中心。k-means 聚類算法的核心思想是把若干數據對象劃分為個聚類，使每個聚類中的數據點到該聚類中心的平方和最小。算法的主要步驟如下：

從若干數據對象中任意選擇個對象作為初始聚類中心。

根據每個聚類對象的均值（中心對象），計算每個對象到這些中心對象的距離，并根據最小距離重新對相應對象進行劃分。

計算每個（有變化）聚類的平均值（中心對象）。

循環Step2、Step3，直到每個聚類不再發生變化為止。

1.2 算法優缺點

k-means 算法的優勢主要有：簡單、易于理解和實現，只需要計算點和簇中心之間的距離即可，所以運算速度非常快；收斂快，一般僅需5～10 次迭代即可；高效，時間復雜度為（**）。

對于k-means 算法存在的問題，可做分述如下：

（1）必須設置簇的數量（預先給定值）。由于是先驗給定的，但值卻往往難于確定，特別是對于大型數據集，在算法啟動前是無法精準給出的。

（2）k-means 算法對初始選取的聚類中心點是敏感的，需要研發出初始隨機種子點啟動算法，且隨機種子點的選取至關重要。不同的隨機種子點得到的聚類結果完全不同。一般從隨機選擇的聚類中心開始執行，可能會在算法的不同運行過程中，產生不同的聚類結果，這也會導致結果無法復現且缺乏一致性。

（3）對噪點過于敏感。因為算法是基于均值的，但均值求取上有時也并不簡單。如：對于球形簇的分組效果較好，而對非球型簇，特別是不同尺寸、不同密度的簇分組效果卻欠佳。如果初始點選擇不當，最終的分組效果就會存在很大的差異，如圖2 所示。

圖2 初始點選擇后的分組效果對比圖Fig.2 Comparison chart of grouping effect of initial points selection

1.3 改進方法總述

針對k-means 算法存的問題，考慮到本文重點研究的學生成績數據庫的實際問題，在開展聚類分析過程中，本文將進行適當的優化，以減少算法缺陷導致的不良結果。

研究中，需選取合適的值，就要用到先驗知識。常見的方法有拍腦袋法、肘部法則（Elbow Method）、間隔統計量（Gap Statistic）、輪廓系數（Silhouette Coefficient）、Canopy 算法等。比照這些方法，本文借鑒選用一種簡單且操作簡便、基于平方誤差的計算方法來確定值。

針對值需事先給定的問題，在沒有先驗經驗的情況下，可采取幾種不同的值嘗試，分別計算平方誤差（值），找到“拐點”。基于平方誤差的計算公式為：

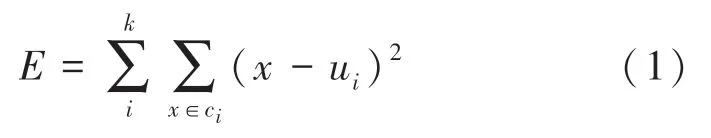
其中，為簇內樣本數，為簇的中心。值越小，說明簇內樣本距離越小，相似度越高。

研究得到的平方誤差曲線如圖3 所示。由圖3可知，當5 時，聚類性能基本達到最優效果；當繼續增加時，性能并沒有明顯變化，則可將最終的聚類算法值選擇為5。

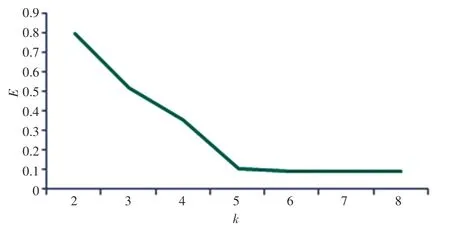
圖3 平方誤差曲線Fig.3 Square error curve

k-means 算法是初值敏感的，選擇不同的初始值可能導致不同的簇劃分規則。如k-means++算法就是針對K-means 聚類算法中隨機選取初始聚類中心的缺陷問題的改進，這是一種基于數據分布選取初始聚類中心的算法，整體上與k-means 算法相差不大，同樣是采取迭代更新的思想。算法的主要改進是在第一步選取個初始聚類中心時，不再是在整個數據集中隨機選取個數據對象作為初始聚類中心，而是遵循初始的聚類中心之間的距離應盡可能遠的原則，選取個初始聚類中心。

借鑒k-means++算法的一些思想，本文對于初始值的選取采用簡化的辦法。在選擇初始點時，可以選擇距離盡可能遠的點；在預處理階段，對數據進行歸一化處理時，可考慮剔除噪點。如果99%的學生成績在20～95 之間，只有1%的學生成績超過95或是低于20，則在做歸一化處理時，可選取99%學生中成績的最高分作為最大值，剩余1%的學生成績直接置為1 即可。

2 實驗結果驗證與分析

現行的以考試成績絕對分數來衡量學生學習狀況的方法比較主觀，且評價方式過于單一。例如：成績在90 分以上為優秀，成績在60 分以上為及格，低于60 分為不及格等。這樣的處理方法雖簡便易行，但存在一些不妥之處，如成績中有用信息未獲重視、成績絕對分值相差不大但劃分后相差很大、總體成績的動態分布情況不合理等現象出現，導致無法公正、合理、有效地評價學生成績。充分挖掘、且利用隱含在學生成績中的有用信息，并采取針對性的措施，如能從學生期中考試成績挖掘出一些預判性的有用信息，并采取積極有效措施，就有可能提高學生的期末考試成績。為此，通過上述聚類方法嘗試進行相關成績分析很有必要。

為了實現系統的可視化，采用Java 與PHP 混合編程，借鑒經典的k-means 聚類算法，優化和改進初始點及值的確定，并同時最大限度地保證系統的穩定性。主要數據源來自北京超星學習通平臺中具體課程相關班級的部分科目期中考試成績，導出數據為Excel 表格形式，成績均為百分制。前期進行數據清洗，主要去除一些無關或空白數據，如學生缺考將會置零并刪除，以免影響聚類結果。

2.1 聚類分析

基于聚類分析的成績劃分是將原有絕對成績劃分改為相對成績的劃分。每個簇組成一個成績群，每個簇中心的數據就是該成績群的中心成績。這些中心成績是學生成績等級劃分的參考標準之一，因此用于學生成績評價也更為準確。通過聚類分析，將學生成績劃歸到各個簇中，簇的大小、形狀、中心值可以用來評價教學效果的好壞。

通常，聚類個數值要盡可能地接近所用的聚類變量的個數。如：5 個變量用于聚類分析，通常就會分為5 個類。類個數太多不利于對類的解釋；太少不利于分開，并降低了類的同質性。比較可行的辦法是每次用不同類的個數來做實驗并對比所得結果，確定最理想的類個數。通過k-means算法聚類劃分學生成績數據，類的個數從1 到8，依次運行一遍，計算類內平方誤差和J（1，2，3，…，8），繪出J和值個數的曲線圖。在J值隨變化的曲線上，其拐點對應的類別數基本接近于最優聚類個數。文中繪制得到的值選取曲線如圖4 所示。由圖4 可見，J隨的增加而單調減少。當值為68 時，J呈平緩狀態，因此可以認為6 是比較合適的聚類個數。

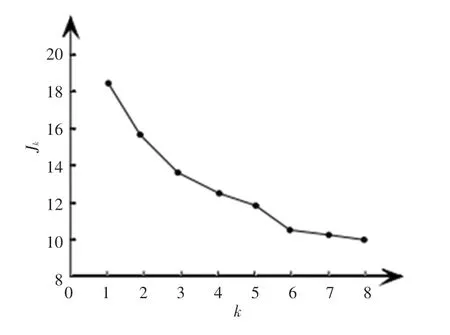
圖4 k 值選取曲線圖Fig.4 k value selection curve

2.2 聚類結果評價

從學生成績數據庫中隨機選擇6 個學生的學習成績作為初始聚類中心，經過k-means 聚類算法生成6 個類別，見表1。

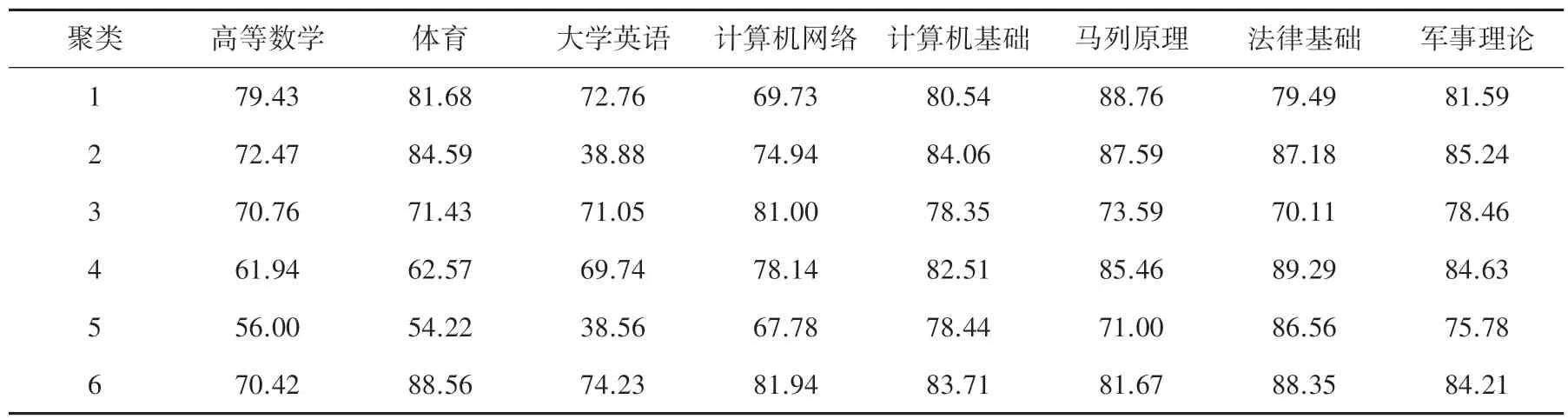
表1 生成的最終聚類中心Tab.1 Generated final cluster centers

在學生成績評價中通過聚類分析發現，每一個類就是一個成績群，處于每個類中心的數據就是該成績群的中心成績。例如：第4 類學生的計算機基礎成績隨中心值82.51 的變化與第6 類學生的大學英語成績隨中心值74.23 的變化如圖5 所示。由圖5 可以看出相近的成績都被劃分到了同一類，避免了采用傳統劃分方法可能出現“學生成績差別不大，劃分后結果可能相差很大”的情況。另外，每一科成績隨中心的變化就是相對于整體成績的分布情況。

圖5 學生成績隨聚類中心變化圖Fig.5 Changes in student grades with cluster centers

總之，該聚類分析不僅可以使學生清楚自己相對于整體成績的位置，還可以體現某類學生在某些學科的不足，從而提醒任課教師采取針對性措施。從表1 中所劃分的類的人數及中心成績可以看出，所有學生前三門基礎學科成績較低，尤其大學英語成績最低，而思政課程的成績就相對較高。同時也可以看出，每一類學生哪些學科成績相對偏低，從而制定有效改進的解決辦法，提高學生期末考試的成績。比如第二類別英語成績最低的這一部分學生，可以反映給學校教務處適當增加英語學科的課時，具體評價解釋見表2。

表2 聚類評價和解釋Tab.2 Cluster evaluation and interpretation

3 結束語

隨著人工智能技術在各類信息化領域中的不斷深入，學習過程中數據源的大量涌現，作為常見的無監督學習的典型算法—k-means 聚類算法，對其在個性化學習系統中開展相關應用研究有著廣闊的前景。本文從經典的k-means 算法出發，探索并尋找一種效率更高、穩定性更好的聚類分析方法，并在個性化學習系統中進行實踐，取得了不錯的應用效果，也為后續的進一步研究提供了有益借鑒。