深海環境下帶球封頭鈦合金耐壓殼碰撞特性研究

俞白兮，余 越，司馬燦

（1.中國船舶科學研究中心，江蘇 無錫 214082；2.深海技術科學太湖實驗室，江蘇 無錫 214082）

0 引 言

耐壓殼作為深海潛器的關鍵組成部分，為人員工作、生活提供空間，其安全性對保障深海裝備和人員生命安全必不可少。隨著深海裝備速度提高、活動范圍擴大，在深海復雜的地貌環境下，潛器深海碰撞成為了不可避免的工程問題。典型的深海碰撞風險對象有礁石、落坡、硬質生物鈣化層等，從而有可能導致潛器發生局部或整體失穩、應力集中的強度破壞等不利后果。因此，在耐壓殼強度、變形及疲勞等經典力學問題研究的基礎上，有必要進一步研究深海潛器在大潛深環境條件下的碰撞力學特性。

現有海洋結構物的碰撞研究主要針對水面船的船-船碰撞及觸礁碰撞，通過數值仿真或試驗分析船舶結構的撞擊響應及損傷變形和破壞模式。文獻[1]基于VLCC 船側結構模型的沖擊實驗，采用有限元方法仿真分析了碰撞及觸底的結構損傷變形、沖擊力歷程及能量耗散；文獻[2-3]基于非線性有限元，模擬了船舶底部擱淺時與礁石的碰撞過程，礁石簡化為剛性體，獲得了船體結構變形、應力響應，提出了降低擱淺損傷的船舶底部結構改進方案；文獻[4-5]數值模擬了船-船碰撞，船舶觸礁的過程，并基于1/2縮比試驗，分析了結構塑性大變形和局部屈曲特性，進行了防撞優化設計；文獻[6]則模擬了不同加筋形式雙層船舶結構的碰撞過程，通過對比撞擊能量響應明確了縱筋形式的結構具有更好的吸能效果。

深海耐壓殼碰撞與水面船的碰撞模式相比存在明顯差別，這是因為耐壓殼在深海受到靜水壓力作用，處于較高的初始應力水平，結構動力學特性發生了明顯改變。但深海耐壓殼的碰撞研究文獻較少，文獻[7]采用Abaqus數值模擬并試驗對比了包含基座的加筋圓柱殼結構受水下爆炸沖擊載荷的動態響應，但未考慮靜水壓力的影響。文獻[8]針對載人潛水器以不同姿態坐底巖石地基時，將巖石視為剛性體，分析非耐壓框架結構的強度及安全性。深海巖土類的撞擊對象作為剛體處理時，會導致耐壓結構的碰撞結果過于保守，失去意義。Zhao[9]考慮靜水壓力影響，仿真計算不同航速下圓柱殼的碰撞強度，但靜水壓力較小（200 m水深），耐壓殼初始應力水平很低。一般來說，通過分析結構的極限承載能力作為耐壓殼撞擊后的失穩判據，應考慮撞擊引起的結構塑性變形和殘余應力這兩個因素的影響。文獻[9]引入撞擊最后時刻的耐壓殼變形，計算結構的極限承載能力，變形中包含塑性變形和彈性變形兩部分，把可恢復的彈性變形考慮在內會導致計算結果存在一定偏差，且未考慮撞擊后殘余應力對極限承載能力的影響。考慮到在高靜水壓力作用下結構的應力水平較高，應力余量小，因此除了失穩，結構的強度破壞也是不可忽視的危險模式。Liu 等[10]利用Dytran 模擬鋼結構雙耐壓殼體受撞擊的過程，定性分析了碰撞過程具有區域性，可能引起凹陷變形、失穩、破壞等多種結果，但沒有將結構失穩和破壞進行定量的統籌考量。文獻[11]考慮大靜水壓力的影響（1500 m 水深），仿真采用高速Hopkinson試驗結果擬合的材料參數，未涉及耐壓殼從低航速遞增過程中結構的碰撞特性變化規律及碰撞過程對結構破壞特性的影響。

考慮到深海潛器碰撞問題的理論研究尚缺少依據，試驗成本和難度較高，因此有限元方法是目前分析水下耐壓殼碰撞問題最經濟、便捷的方式。當模型網格尺寸合適，材料和結構與實際相符的條件下，利用非線性有限元軟件對可能產生大變形的結構進行碰撞模擬的結果與試驗結果具有相當高的一致性[12]。本文采用Abaqus 仿真軟件，數值模擬鈦合金帶球封頭環肋圓柱殼耐壓結構與平板構型玄武巖的大潛深碰撞過程及響應，分析球封頭上塑性缺陷和殘余應力對結構極限承載能力的影響，定量描述中低航速下不同速度、不同深度對結構失穩模式、極限承載能力、強度破壞的影響規律，統籌考量耐壓殼失穩、破壞的安全衡準。

1 計算模型

1.1 碰撞模型及參數

1.1.1 耐壓結構

碰撞計算分析選取的耐壓結構如圖1所示，總長12.8 m，由環肋圓柱殼和兩端的半球封頭組成，殼體內外均設有T型肋骨，其中內肋骨21根，外肋骨5根，具體參數見表1。

表1 耐壓殼結構參數Tab.1 Structural parameters of the pressure hull

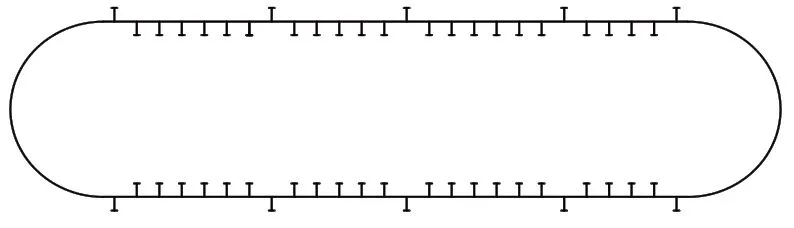
圖1 帶球封頭的環肋圓柱殼耐壓結構示意圖Fig.1 Structural model of cylindrical pressure shell with semi-spherical heads

目前，學者們多用Johnson-Cook（J-C）唯象本構模型模擬TC4鈦合金材料的動態力學行為。經TC4材料不同本構模型的對比[13]，J-C本構模型具有與試驗更好的吻合度，其本構方程具體表達式為

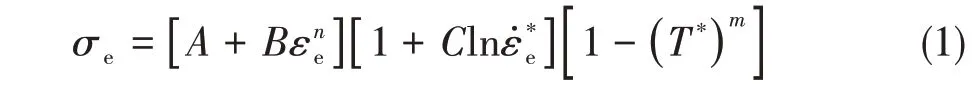
式中，σe為等效應力，A為參考應變率和參考溫度下的屈服應力，B、n為應變硬化系數，εe為等效塑性應變，C為應變率敏感系數，為無量綱應變率，m為溫度敏感系數，T*為無量綱溫度。

式（1）三項分別考慮了應變強化、應變率硬化及溫度軟化效應對材料動態力學性能的影響。Kay[14]和陳剛[15]基于J-C 本構模型及試驗獲取的不同溫度和不同應變率下的TC4 材料力學行為，采用撞擊試驗和數值模擬驗證了模型參量的準確性。考慮到本文模擬對象為大型結構的低速碰撞過程，針對大型結構的低速碰撞過程可采用準靜態方法，忽略應變率效應的影響[16]。考慮到研究的碰撞過程處于深海低溫環境，因此忽略J-C 本構模型中的應變率效應和溫度效應，僅考慮材料的應變強化效應。鈦合金材料的J-C 參數由TC4 試樣準靜態拉伸試驗獲取。鑒于鈦合金材料的塑性較差，強度極限與屈服極限較接近，在忽略應變率效應的情況下以TC4試樣準靜態拉伸的強度極限960 MPa作為結構強度破壞的衡準。耐壓殼材料的具體本構參數及物理參數見表2。

表2 TC4材料參數Tab.2 Material parameters of TC4

1.1.2 玄武巖

撞擊對象選擇海洋分布最廣泛的硬質巖石——玄武巖。海底巖石形狀復雜，Sormunen[17]在研究海洋碰撞計算中采用二次多項式、圓錐曲線等數學模型描述海底巖石縱剖面構型，當海底巖石尺度相對耐壓結構較大時可將巖石簡化為平板形式。另外，巖土力學中常用Mohr-Coulomb 屈服準則描述巖土的本構行為[18-19]，該準則表述為：介質微元的任何截面上剪應力τn的大小超過臨界值時材料發生屈服。不同于Tresca 屈服準則，此臨界值并非常數，而與微分面上的正應力σn、粘聚力C及摩擦角?相關[20]，其表達式為

本文選用文獻[21]中玄武巖的Mohr-Coulomb 參數作為計算輸入。按照文獻[19]，玄武巖的失效模式不僅與巖石間的薄弱層厚度有關，而且與受載荷方向的層間連接角度有關，數值計算中精細建模難度較大。考慮到本文研究側重耐壓殼的碰撞特性，為簡化計算模型，忽略玄武巖的失效模式。玄武巖模型參數見表3。

表3 玄武巖模型參數Tab.3 Material parameters of basalt

1.2 數值模型

依據1.1節中的結構與材料參數，用Abaqus仿真軟件分別建立耐壓殼和玄武巖數值模型，其中玄武巖構型簡化為12 000 mm×12 000 mm×2000 mm 平板，如圖2 所示。耐壓殼及其肋骨均采用四邊形殼單元；玄武巖結構采用六面體單元。依據文獻[22]數值模擬船體外板撞擊過程的網格劃分原則，本文選取100 mm 的單元尺寸時具有較好的計算收斂性。殼單元和六面體單元總數量分別為30 328 和288 000。為簡化計算模型，依據文獻[23]，不考慮流固耦合即忽略撞擊過程中水介質負載及能量耗散的作用，這樣的簡化模型可以得到偏安全的結果。

圖2 碰撞數值模型Fig.2 FE collision model

首先采用Abaqus 中的顯式動力學分析模塊（Explicit）模擬鈦合金耐壓殼球封頭與玄武巖的碰撞過程，獲得耐壓殼的撞擊應力、變形響應。封頭與玄武巖的接觸離散設置為“面對面”（surface to surface），一般來說，這種方式能得到更準確的接觸壓力和接觸應力結果[24]。

Abaqus提供了從顯式到隱式的分析結果傳遞功能，顯式動力學分析完成后，引入撞擊最后時刻的鈦合金耐壓殼構型和應力狀態進行極限承載能力分析，其中只有耐壓殼塑性變形影響結構的極限承載能力，引入構型時需移除結構的彈性變形部分。極限承載能力分析分為兩個步驟：第一步分析結構線性屈曲（buckle），用于結構最大臨界載荷和屈曲模態的評估，也用作缺陷幾何引入的模態分析；第二步分析非線性屈曲（riks），用于評估結構的最大臨界載荷及后屈曲形態，需將線性分析中的一階模態以初始幾何缺陷的形式引入非線性屈曲分析中，保證屈曲分析中的載荷-位移曲線連續而不出現分叉，最終計算得到的臨界載荷即是撞擊后耐壓殼的極限承載能力。數值計算流程如圖3所示。

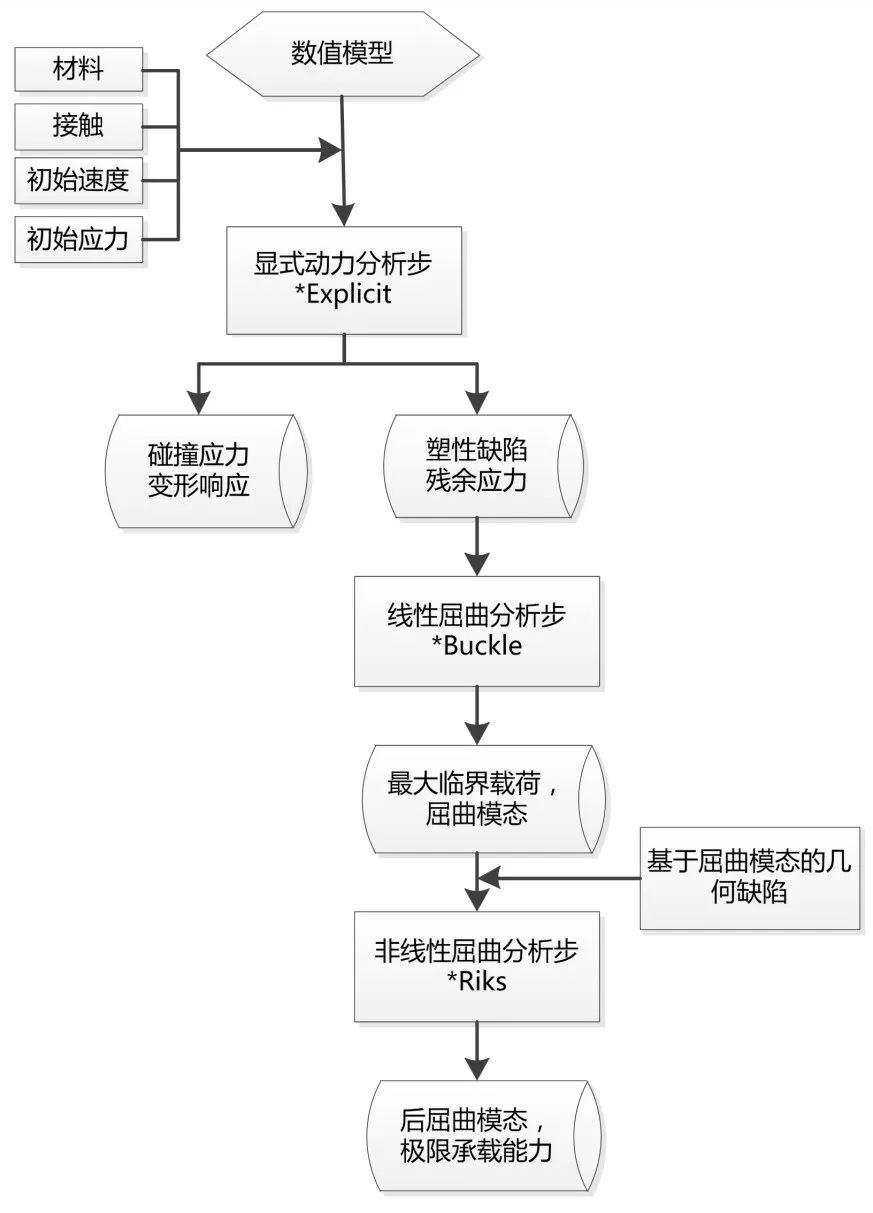
圖3 數值計算流程Fig.3 Numerical calculation procedure

耐壓殼的初始應力來自靜水壓力的作用，Abaqus顯式分析中靜水壓力的加載方式會影響計算精度。加載速率過快導致耐壓殼發生應力震蕩，使計算結果不準確，因此人為控制靜水壓力自0時刻至0.1 s時刻以線性遞增的方式施加在耐壓殼并持續到撞擊結束。這樣，為保證球封頭在靜水壓力完全加載后再與玄武巖發生碰撞，賦予耐壓殼一定的初速度，根據不同撞擊速度在耐壓殼與玄武巖之間設置不同間距，控制球封頭在0.2 s時刻垂直撞擊玄武巖平板。

2 碰撞特性分析

2.1 碰撞過程分析

按照前文所建模型及流程進一步模擬深度為750～1500 m 時，耐壓殼在0.5～8 kn 航速下球封頭與玄武巖平板的碰撞過程，并統計各工況下結構的應力、變形響應。在750 m 水深、0.5 kn速度撞擊計算工況中，顯式計算0.1 s 時刻完成對耐壓殼7.5 MPa 靜水壓力的施加，該時刻耐壓殼的應力云圖如圖4所示。同時，通過隱式靜力分析計算獲得耐壓殼受7.5 MPa靜水壓力作用下的應力狀態，如圖5所示。顯式和隱式靜力分析中靜水壓力的作用結果一致，表明碰撞分析中靜水壓力以0～0.1 s線性遞增的加載方式是準確有效的。

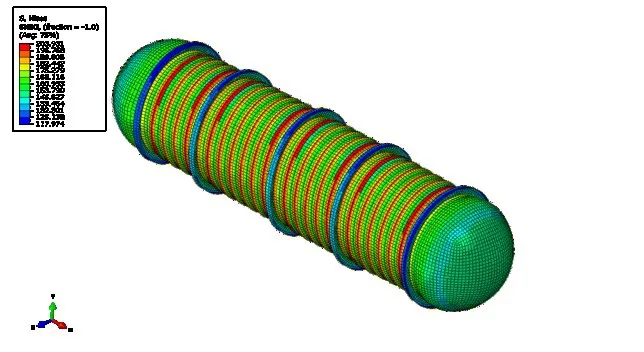
圖4 顯式分析0.1 s時刻耐壓殼受7.5 MPa靜水壓力von Mises應力云圖Fig.4 von Mises stress of the pressure hull in explicit analysis(Time=0.1 s,Hydrostatic pressure=7.5 MPa)

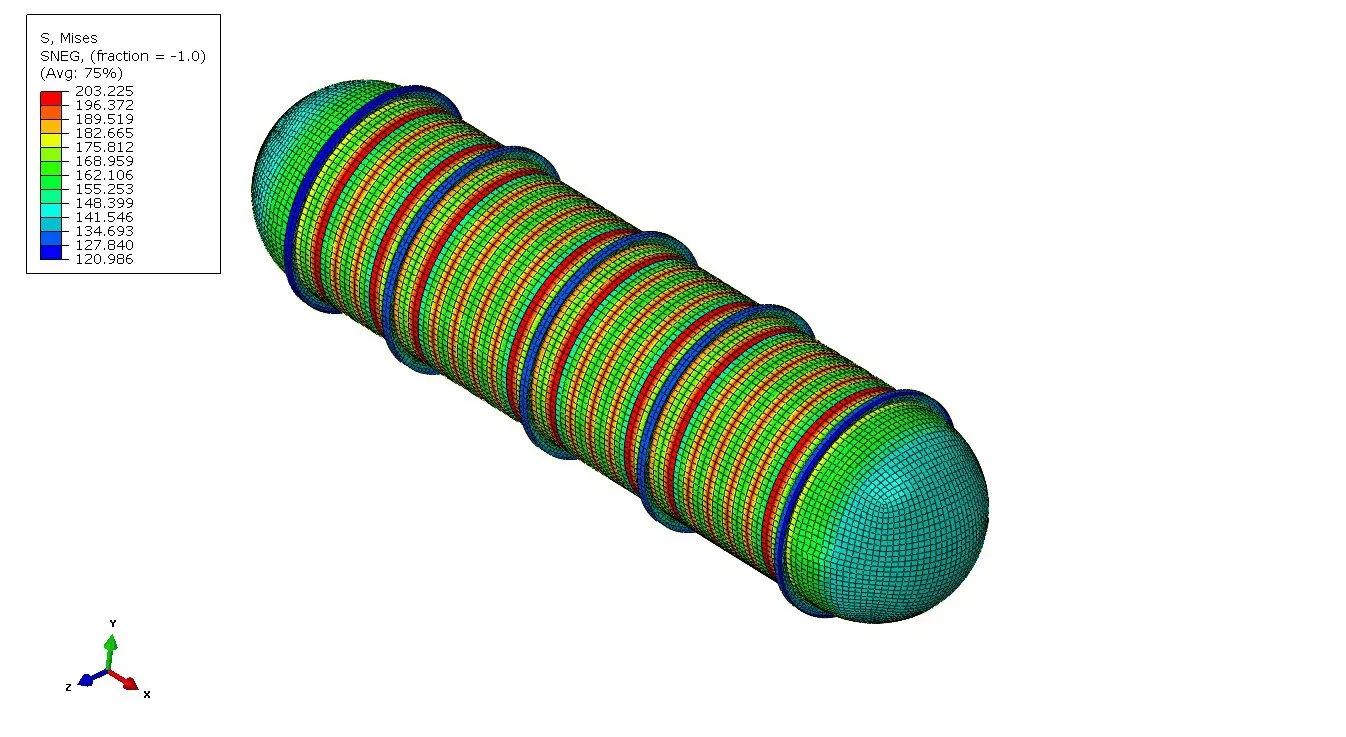
圖5 隱式分析耐壓殼受7.5 MPa 靜水壓力von Mises應力云圖Fig.5 von Mises stress of the pressure hull in implicit analysis(Hydrostatic pressure=7.5 MPa)

0.2 s時刻耐壓殼球封頭與玄武巖接觸，伴隨球封頭與玄武巖之間不斷接觸擠壓，封頭局部的應力水平迅速增加，最高達到516.6 MPa，同時封頭上出現一定程度的凹陷變形，此時除接觸球封頭以外的其它結構部分應力水平與碰撞前基本相當，如圖6 所示。碰撞接觸持續了約0.04 s，而后耐壓殼整體回彈，伴隨球封頭與玄武巖逐漸分離，接觸部位的應力水平開始下降。由于耐壓殼局部應力峰值516.6 MPa未超過材料的屈服極限，變形仍處于線彈性狀態，球封頭與玄武巖分離后，耐壓殼的構型和應力水平恢復到碰撞接觸前的狀態。

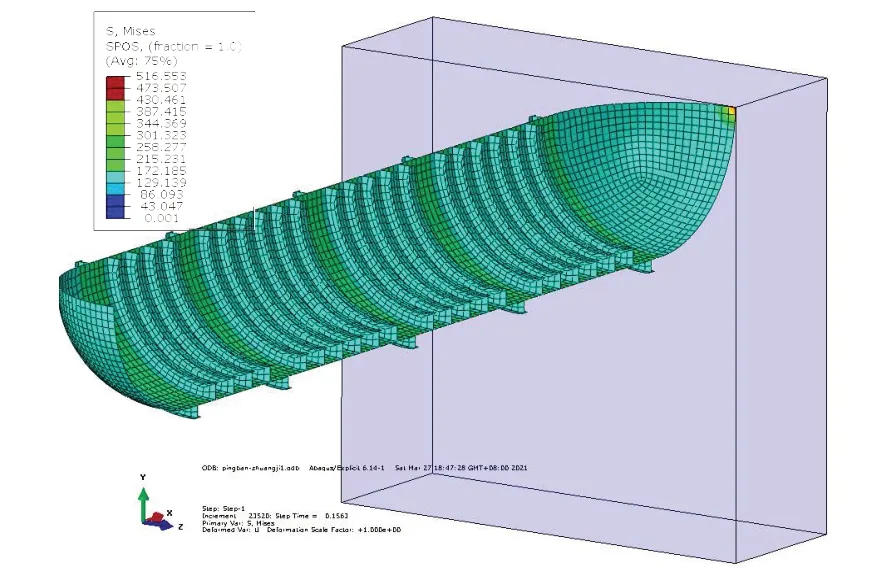
圖6 封頭撞擊最大von Mises應力云圖（速度0.5 kn，深度750 m）Fig.6 Maximum von Mises stress at impact area(Velocity=0.5 kn,Water depth=750 m)

在750 m 水深下航速提高到1 kn時，耐壓殼球封頭在與玄武巖的接觸過程中，計算得到的局部應力最高達到824.8 MPa，超過材料的屈服極限，此時變形已處于彈塑性狀態，如圖7 所示。伴隨球封頭與玄武巖分離，耐壓殼的構型和接觸局部的應力水平并不會恢復到碰撞前的狀態。分離時刻球封頭碰撞接觸中心存在最大1.61 mm 的彈塑性凹陷變形和最大173.2 MPa 的局部應力，高于碰撞前封頭上約147 MPa的應力水平。提取撞擊響應中的塑性部分，球封頭局部存在最大0.01 mm的塑性缺陷和最大45.2 MPa的殘余應力。

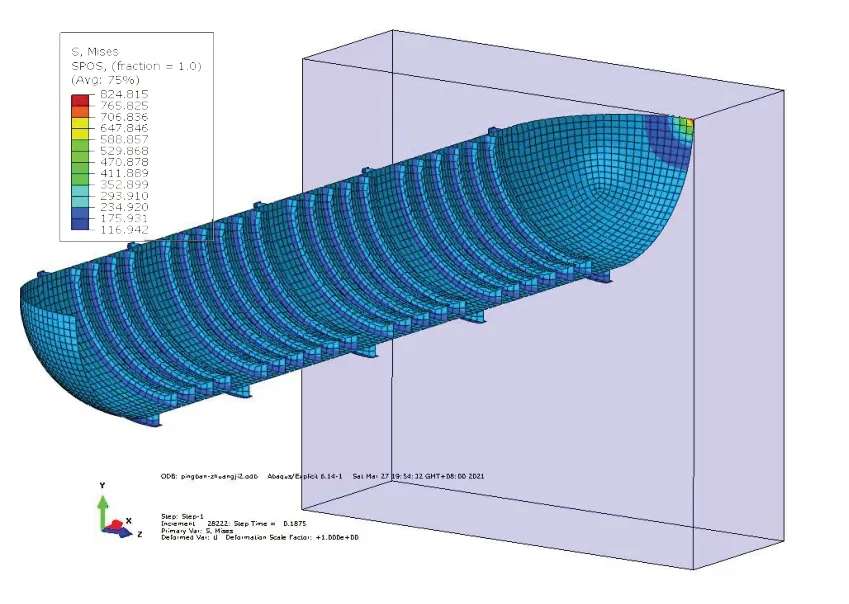
圖7 封頭撞擊最大von Mises應力云圖（速度1 kn，深度750 m）Fig.7 Maximum von Mises stress at impact area(Velocity=1 kn,Water deptch=750 m)

圖8～9 分別給出了接觸過程中球封頭最大von Mises 應力和最大塑性缺陷隨不同水深、不同速度的變化趨勢。1 kn及以上航速時，碰撞處于彈塑性狀態，球封頭的變形隨著速度的增長不斷增加。與0.5 kn 航速相比，耐壓殼球封頭的von Mises 峰值應力從1 kn 開始階躍式上升，而后上升趨勢變緩，伴隨航速的增加呈近似線性的增長，在750 m、1 000 m、1 250 m、1 500 m 水深時，耐壓殼封頭碰撞局部分別在7.5 kn、7 kn、6.5 kn、5.5 kn 時超過材料960 MPa 的強度極限，發生強度破壞。在未發生強度破壞的情況下，碰撞分離后球封頭撞擊區域出現塑性缺陷和殘余應力，其它區域的應力水平和幾何形態基本和撞擊前一致。碰撞速度愈大，靜水壓力愈大，結構上的von Mises 峰值應力和塑性缺陷愈大，球封頭發生強度破壞的速度愈低，并且耐壓殼球封頭的撞擊具有局部性的特征。

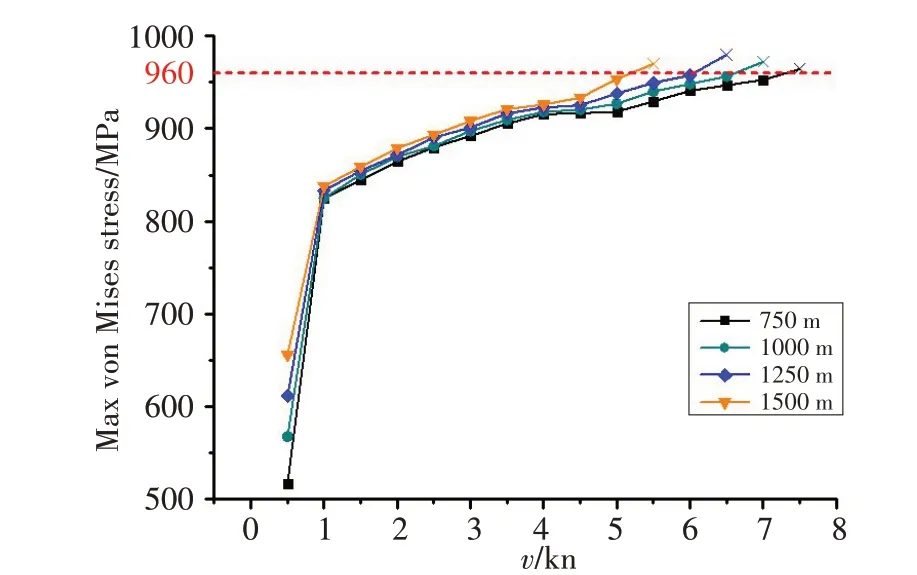
圖8 不同速度、深度耐壓殼球封頭von Mises峰值應力Fig.8 Maximum von Mises stress at different velocities and depths

圖9 不同速度、深度耐壓殼球封頭碰撞最大塑性缺陷Fig.9 Maximum plastic defect at different velocities and depths

2.2 耐壓結構失穩分析

考察球封頭上殘余應力和塑性缺陷對失穩模式、極限承載能力的影響。首先單獨研究殘余應力的作用，選取750 m 水深、5 kn 航速碰撞工況最后時刻的耐壓殼響應作為分析輸入，如圖10 所示。方案一包含球封頭最大3 mm 塑性缺陷，不包含撞擊局部的殘余應力；方案二不僅包含球封頭的塑性缺陷，也繼承了撞擊最后時刻局部最大734.7 MPa von Mises 應力狀態。在Abaqus 中通過非線性屈曲分析（riks）計算得到方案一和方案二耐壓殼的極限承載能力分別為51.2 MPa 和53.7 MPa，殘余應力有2.5 MPa的正向影響，使極限承載能力增加了約4.9%。因為失穩是結構受壓直至無法保持原有的平衡狀態而導致的，彈塑性撞擊引起球封頭局部產生以拉伸狀態為主的殘余應力，能夠抵消結構艏部受到的部分壓縮載荷，從而一定程度地提高了結構的承載能力。因此在工程設計中簡化計算，分析耐壓殼撞擊后的極限承載能力時忽略殘余應力的影響，可以得到偏保守的計算結果。

圖10 殘余應力對失穩分析影響對比方案Fig.10 Comparative schemes of buckling analysis on residual stress

根據上述分析結果，研究耐壓殼碰撞后的失穩模式和承載能力時僅需考慮撞擊塑性缺陷的影響。為得到更準確的計算結果，疊加結構線性屈曲分析（buckle）的一階模態幾何缺陷，采用riks 分析計算耐壓殼在不同塑性缺陷下的極限承載能力。在750 m 水深時，不同撞擊速度工況下耐壓殼極限承載能力的變化規律，可以分為三種情況，如圖11所示。

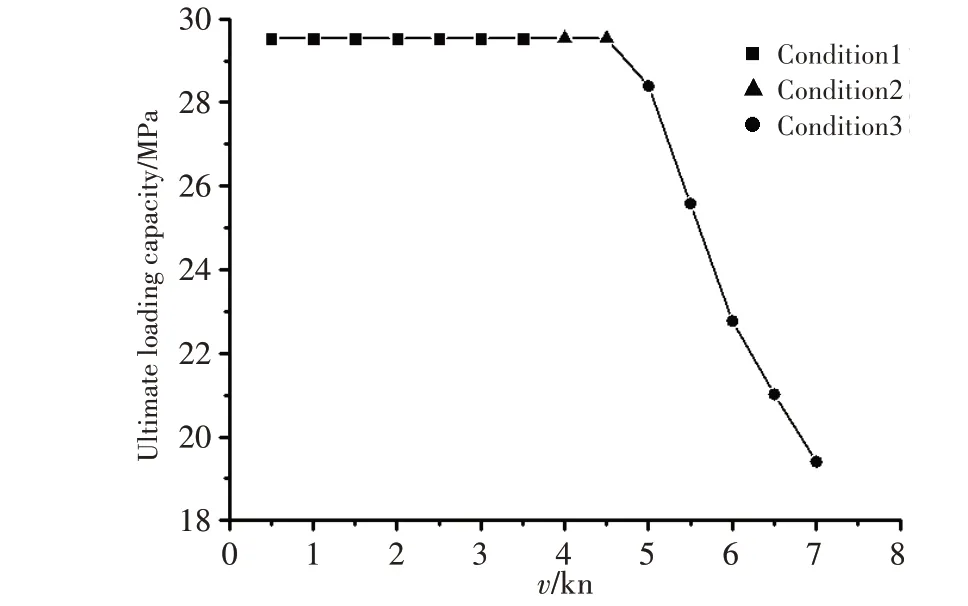
圖11 750 m水深不同撞擊速度下耐壓殼的極限承載能力Fig.11 Ultimate loading capacity of the pressure hull at different velocities(Water depth=750 m)

情況一：0.5 kn航速時耐壓殼的碰撞處于線彈性狀態，非線性屈曲分析時無初始塑性變形和應力，極限承載能力為29.535 MPa，此時失穩發生在耐壓殼柱段，如圖12 所示。隨著撞擊速度的增加，雖然耐壓殼艏部產生隨速度增大的塑性缺陷，但由于球封頭結構形式的特殊性，封頭處于“無矩”狀態，殼板厚度方向只承受均勻的壓縮載荷，不承受彎矩引起的正應力，因此球封頭是較圓柱段更強的承力結構[25]。所以在3.5 kn及以下的速度下，當球封頭碰撞區域的塑性缺陷較小時，失穩仍發生在圓柱段，極限承載能力保持為29.535 MPa。

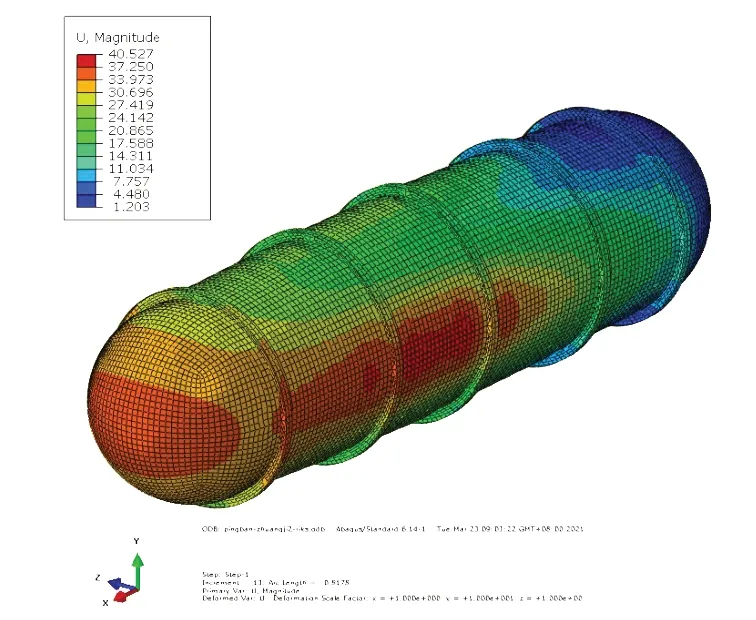
圖12 750 m、0.5 kn工況下耐壓殼失穩模式Fig.12 Buckle mode of the pressure hull(Velocity=0.5 kn,Water depth=750 m)

情況二：耐壓殼在750 m 水深、4 kn 撞擊工況下的失穩模式如圖13 所示，此時失穩模式隨著塑性缺陷的增大而發生改變，變為在艏部撞擊缺陷處發生失穩。但由于球封頭具有更強的承壓能力，此時極限承載能力仍保持29.535 MPa，并未降低。4.5 kn的情況與4 kn相同。

圖13 750 m、4 kn工況下耐壓殼失穩模式Fig.13 Buckle mode of the pressure hull(Velocity=4 kn,Water depth=750 m)

情況三：5 kn 及以上航速時，球封頭撞擊處的初始塑性缺陷已比較大，極限承載能力開始迅速下降，失穩始終發生在球封頭處，在7 kn 航速時的失穩模式如圖14 所示，此時極限承載能力降低至19.41 MPa。耐壓殼在7.5 kn及以上航速下，耐壓殼球封頭在撞擊過程中已超過材料強度極限，發生強度破壞，故不做失穩分析。

圖14 750 m、7 kn工況下耐壓殼失穩模式Fig.14 Buckle mode of the pressure hull(Velocity=7 kn,Water depth=750 m)

以各深度下耐壓殼碰撞發生強度破壞的航速為截止量，耐壓殼不同潛深下的極限承載能力隨撞擊速度的變化均可劃分為上述三種情況，如圖15所示。深度越大，失穩模式將在越小的速度下由圓柱段轉移到球封頭，極限承載能力在更低的速度下即發生下降。根據計算結果，一般耐壓殼球封頭最大塑性缺陷約為13 mm時結構極限承載力開始下降。

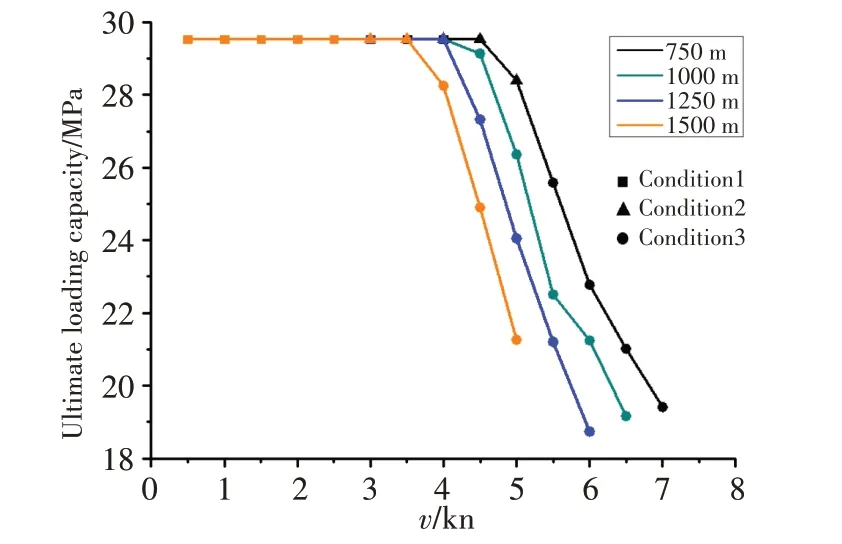
圖15 不同水深、不同撞擊速度下耐壓殼的極限承載能力Fig.15 Ultimate loading capacity of the pressure hull at different velocities and depths

2.3 耐壓結構失穩、強度破壞分析

統籌考慮耐壓殼失穩破壞和強度破壞分析結構的安全性。由2.1 節可知，耐壓殼球封頭在750 m、1 000 m、1 250 m、1 500 m 深度下，分別于7.5 kn、7 kn、6.5 kn、5.5 kn 速度時在撞擊接觸過程中von Mises 應力峰值超過材料強度極限，視為發生強度破壞。因此，考察耐壓殼在750～1500 m 水深下未發生強度破壞時最低的極限承載能力，均發生在臨近強度破壞的速度下，分別為7 kn、6.5 kn、6 kn和5kn。深海耐壓結構的整體失穩破壞，一般取1.2 倍的安全系數作為安全衡準。耐壓殼的失穩安全校核結果見表4，可以發現航速低于發生強度破壞的速度時，耐壓殼撞擊引起的塑性缺陷和殘余應力雖然導致極限承載能力下降，但仍滿足結構的失穩安全性要求。因此，在深海耐壓結構的工程設計中，當考慮結構球封頭處的碰撞破壞模式時，應主要考慮結構的強度破壞，而非失穩破壞。

表4 耐壓殼極限承載能力校核Tab.4 Ultimate loading capacity check of the pressure hull

3 結 論

本文采用Johnson-Cook 本構模型與Mohr-Coulomb 本構模型分別模擬鈦合金與玄武巖材料，利用Abaqus仿真軟件計算了大潛深下TC4鈦合金環肋圓柱殼耐壓結構球封頭與玄武巖平板垂向撞擊的動態過程，分析了不同潛深和航速情況下耐壓殼的變形、應力響應及碰撞失穩、破壞特性。研究結果表明：

（1）伴隨下潛深度、航速的增加，撞擊由彈性階段進入彈塑性階段并體現較強的局部性。撞擊區域塑性缺陷和von Mises 峰值應力隨深度、航速的增大而上升，深度愈大，耐壓殼撞擊區域發生強度破壞的航速愈低。深度從750 m增加到1500 m，強度破壞的航速從7.5 kn下降到5.5 kn。

（2）撞擊引起的耐壓殼球封頭塑性缺陷和殘余應力對極限承載能力有影響。封頭上拉伸狀態為主的殘余應力對耐壓殼的承壓起正向作用，可在工程設計中忽略該因素對失穩的影響。耐壓殼失穩隨航速的變化可分為三種情況：線彈性碰撞或碰撞塑性缺陷較小，圓柱段失穩，承載能力不變；隨著塑性缺陷增長，失穩模式轉移至球封頭凹陷處，承載能力不變；最大塑性缺陷超過約13 mm時，球封頭失穩，承載能力迅速下降。

（3）耐壓殼深海撞擊安全性應統籌考慮結構的失穩破壞和強度破壞。在發生強度破壞前耐壓殼的極限承載能力始終高于失穩的安全衡準，工程設計中考慮鈦合金耐壓殼球封頭的碰撞破壞模式時，應主要考察結構的強度破壞。

后續可擬合低應變率下的鈦合金Johnson-Cook 本構參數用于提高數值模擬精度，并進一步考慮玄武巖分層結構及棱錐形碰撞接觸面，研究環肋圓柱殼柱段碰撞時的耐壓殼失穩、破壞模式以及流體負載的影響。