深海作業平臺動力定位中的水動力問題分析

胡芳琳，馬向能，馮康佳

（1.中國船舶科學研究中心，江蘇 無錫 214082；2.深海載人裝備國家重點實驗室，江蘇 無錫 214082）

0 引 言

動力定位的研究，多見于水面動力定位船舶和海洋平臺，水下平臺的研究較少。對于水下動力定位，相關研究較多的是低速纜控作業潛器ROV 的動力定位。水下動力定位與水面動力定位主要存在兩個方面的不同：第一是水面動力定位一般考慮水平面三個自由度，而水下動力定位需要考慮六個自由度，自由度的增加會導致控制手段多樣、控制方式復雜；第二是水面受到風、浪、流外界環境的干擾力，而水下考慮較多的是海流干擾。此外，深海作業平臺在布放纜控類作業潛器進行作業時，還會受到纜繩傳遞而來的載荷；深海作業平臺在回收作業潛器過程中，作業潛器與平臺彼此相互干擾，為了確保回收成功，平臺需要在抗干擾過程中保持一定的定位精度。

水下動力定位最主要的水動力問題是數學模型的建立。在目前文獻中，針對低頻類運動，水面船、海洋平臺和水下低速類作業潛器如ROV 等，有研究者采用復雜非線性方程[1-7]，但大多數采用的是Fossen[8]提出的簡化線性模型[9-15]和簡化非線性模型[16-18]。數學模型中水動力系數的獲取主要有如下方法：一是采用水動力模型試驗測量獲得，如拖曳水池模型試驗、風洞模型試驗、旋臂水池模型試驗、PMM動態模型試驗等[1-3]；二是采用數值模擬技術進行預報[19-22]，目前主要基于RANS和URANS方程進行求解；三是在有大量數據積累的基礎上通過總結出的經驗公式或擬合公式計算獲得[4-6,15,23]，這類方法在水面船上比較常見；四是參數識別法[3,8,24]。第二種方法大多需要經過試驗驗證，第三種方法涉及到大量數據積累，也需要基于試驗研究，第四種參數識別法需要進行自航模試驗或實船試驗才能得出，因此目前最主要最可靠的方法還是水動力模型試驗。

從上述文獻可知，對于動力定位研究而言，尤其是水面動力定位研究而言，非線性模型能夠獲得較好的結果，但簡化線性模型也能滿足要求，因此使用普遍。但文獻中對于簡化線性模型的表達不盡相同，比如有些文獻會忽略附加質量科氏力，進一步地，還有文獻會忽略剛體質量科氏力，也有些文獻對這兩類科氏力均不忽略。關于忽略的理由，一般認為對控制影響很小，但影響到底多小，卻很少有文獻進行數據說明。此外，無論是線性模型還是非線性模型，大都是基于船舶或潛艇操縱運動方程的簡化，沒有從動力定位本身的特點去分析和建立。本文從水動力角度對動力定位問題進行分析，以期建立更適用于水下動力定位的數學模型，并闡明剛體質量或附加質量科氏力的影響。

1 動力定位中的水動力問題分析

懸停在深海中的作業平臺，普遍會受到海流作用，平臺易處于大攻角大漂角環境中，此時平臺主要受到“與速度相關的水動力”，產生的力和力矩使站體發生移動和轉動。平臺一旦發生運動，將同時受到“與速度、加速度、角速度、角加速度相關的水動力”，形成位移或角位移。要做到定位，應加入動力的主動控制。動力定位，即利用推進器推力輸出的作用，將位移和姿態都調整至目標狀態內。

實際情況中，海流變化緩慢，可視作定常海流來處理，因此海流速度就可以轉換成相對速度的概念納入數學模型中。處在海流中的作業平臺通過推進器推力的合理分配，可有效抵消定常海流帶來的影響，使平臺達到懸停平衡狀態,也是目標狀態。在該狀態下，再疊加考慮外界擾動，產生新的運動，形成新的水動力增量，該新的水動力增量是本文重點研究內容，然后建立數學模型來進行運動仿真。這是針對海流環境中再加入外界擾動的動力定位問題的較為簡單的描述。從中可以看出，基準狀態不再是傳統的直航狀態，而是平衡定常海流后的懸停狀態。問題在于緩慢變化的海流雖然可以視作定常海流，但相對于平臺來說它的方向是不確定的，可從前方來、從后方來、或從側面來等等，因此基準狀態實際上是不確定的。如基準狀態不確定，干擾形成的水動力增量也就無法準確獲取。考慮到深海作業平臺處于深海，海流速度很小，一種簡化處理的方法是直接忽略微速的海流，將基準狀態定為無相對速度的原地懸停狀態；還有一種簡化處理方法是主動調整平臺朝向，使平臺處于迎流平衡的原地懸停狀態，然后進行水下作業過程中擾動問題的求解，這與傳統直航基準狀態類似，唯一的區別就在于基準航速是微速。第一種簡化也可以認為是第二種的特例，即基準航速為零。

經上面的簡化處理后，深海作業平臺動力定位數學模型的求解可分成兩部分：一是定常海流作用下穩定狀態求解；二是外界隨機擾動下的運動與控制求解。在動力定位數學模型中將迎流平衡定常微速海流的懸停狀態作為其初始基準狀態，因此整個過程可以理解為迎流平衡狀態下的擾動及控制過程。此時的擾動不再包含定常海流，定常海流形成的已知載荷直接用一部分推力平衡掉。如前所述，懸浮在海洋中的深海作業平臺可能會受到內波和纜繩脈沖載荷作用，這些擾動易使平臺產生振蕩運動。動力定位對于平臺的姿態和位移控制具有較高要求，位移和姿態上的變化一般會嚴格限制在小幅度變化范圍內。擾動一旦產生，控制將立即進行“回復”。基于上述假設與分析，可采用微速迎流狀態下的小幅度振蕩運動來分析深海作業平臺動力定位過程中的水動力特性。

2 動力定位數學模型

2.1 數學模型通用形式

在隨體坐標系下，通用數學模型為[8]

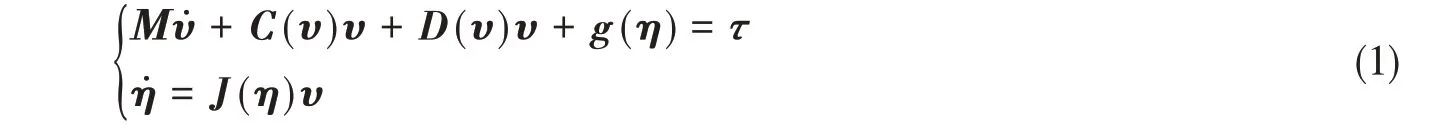
式中：M=MRB+MA，MRB表示剛體質量矩陣，MA表示附加質量矩陣；C(υ)=CRB(υ)+CA(υ)，CRB(υ)表示剛體質量引起的科氏力與向心力矩陣，CA(υ)表示附加質量引起的科氏力與向心力矩陣；υ=[u,v,w,p,q,r]T，u、v、w、p、q、r分別是隨體坐標系六個自由度上的速度和角速度分量；D(υ)表示運動過程中受到的水動力，扣除了附加質量相關項，即扣除了?項和CA(υ)υ項；g(η)表示回復力,η=[x,y,z,φ,θ,ψ]T，x、y、z、φ、θ、ψ是大地坐標系六個自由度上的位移分量；J(η)為坐標轉換矩陣；τ表示環境載荷、推力或注排水引起的靜力變化等。若考慮定常海流環境，那么通用數學模型可采用相對速度的表達方式進行描述：

式中，υr和υc分別為隨體坐標系下的相對速度和海流速度，υr=υ-υc，υcE為大地坐標系下的海流速度，視作常數。此時τ中不再含海流作用力τc，海流作用力以阻尼力形式出現在阻尼項D(υr)υr中。根據式（2）求解出υr后，平臺擾動速度為

2.2 動力定位數學模型中水動力項及水動力系數的獲取

根據上述動力定位過程的分析，重點考慮小幅度振蕩運動中作業平臺的受力，因此可忽略非線性項和非線性耦合項。根據深海工作平臺實際工作的深海海域的海流速度實測數據，確定零速至某微速的海流速度范圍，比如[0 kn，0.5 kn]。在該變化范圍內，計算分析不同速度狀態下各自由度振蕩運動的水動力結果，形成動力定位模型中的水動力項及相應的水動力系數。較低的雷諾數狀態下水動力系數不再是趨于穩定的常數值，但不同微速下有量綱的水動力預報結果差異較小，因此面對未知的海流環境，可根據不同微速下有量綱的水動力預報結果來框定出模型參數攝動的上下界，作為后續控制方法魯棒性研究的輸入。本文采用零速時振蕩運動的水動力結果對水動力項及水動力系數進行介紹，并為后面的運動仿真分析提供輸入。

根據某型深海作業平臺的計算，忽略量級較小的水動力，并結合外形左右對稱的特點，得到如下水動力阻尼矩陣D和附加質量矩陣MA：

矩陣中各元素均為帶量綱的水動力系數，下標υ=0 表示在航速0 kn 時原地振蕩運動得到的水動力結果。

2.3 動力定位數學模型中其他項的表達

數學模型中剛體質量矩陣MRB表達為

式中，m為平臺質量，xG、yG和zG是隨體坐標系下平臺質心坐標，Ix、Iy和Iz為平臺慣性矩，Ixy、Ixz、Iyx、Iyz、Izx和Izy為平臺慣性積。剛體質量的科氏力和向心力矩陣為

回復力矩陣g(η)為

附加質量的科氏力和向心力矩陣見2.4節中的描述。

τ可以主要分成外界環境中的隨機干擾、纜繩的張力干擾、平臺推進器推力輸出和注排水引起的靜力變化，前兩項為干擾項，后兩項為主動控制項。本文重點分析動力定位中的水動力問題，并對干擾形成的運動進行仿真，因此τ包含干擾和平衡海流載荷的推力。

2.4 附加質量科氏力和向心力矩陣

目前在水池模型試驗中，并沒有把附加質量科氏力和向心力從水動力中剝離出來，因此這一部分受力是含在水動力阻尼項中的。

以動態PMM試驗中的純升沉運動為例。縱傾力矩方向測得的主要水動力一般為

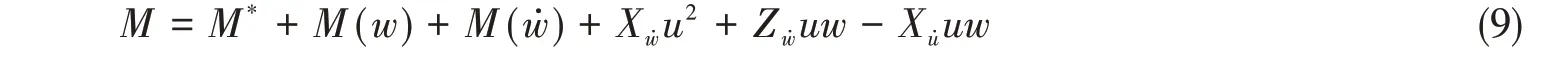
式中：M*+M(w)屬于水動力阻尼項，M(w?)屬于附加質量慣性力項；而Xw?u2+Zw?uw-Xu?uw屬于附加質量科氏力項，其中Zw?uw-Xu?uw被稱為孟克力矩。令M(w)≈Mw·w，M(w?)≈Mw?·w?，則式（9）可表達成

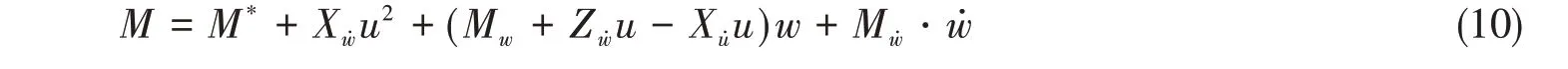
在進行水池試驗結果處理時，(Mw+Zw?u-Xu?u)中各項不一一區分，全部納入Mw中，也意味著CA(υ)υ矩陣中Zw?uw-Xu?uw已經計入到阻尼矩陣D(υ)υ中，因此CA(υ)υ中這一項要設置為0，否則將重復計算這一部分力矩。

其他水動力系數在取值時，也存在類似情況。這樣處理的結果表明，數學模型中，CA(υ)υ需按零值處理。也有文獻報道在設計水動力試驗時將附加質量的科氏力和向心力從水動力中剝離出來[3]，這種情況下應正常計算CA(υ)υ。值得注意的是，由于在空氣中運動時附加質量可以忽略，因此風洞試驗結果中可認為沒有包含CA(υ)υ。當風洞試驗結果和水池試驗結果綜合起來一起考慮時，需要注意這些區別。

本文給出的水動力預報結果沒有將附加質量的科氏力和向心力從水動力中剝離出來，因此數學模型中CA(υ)υ均為0。

3 擾動仿真分析

3.1 研究對象

研究對象所需的相關參數如表1 所示，其中附加質量系數和線性水動力均通過原地振蕩運動數值預報得到。

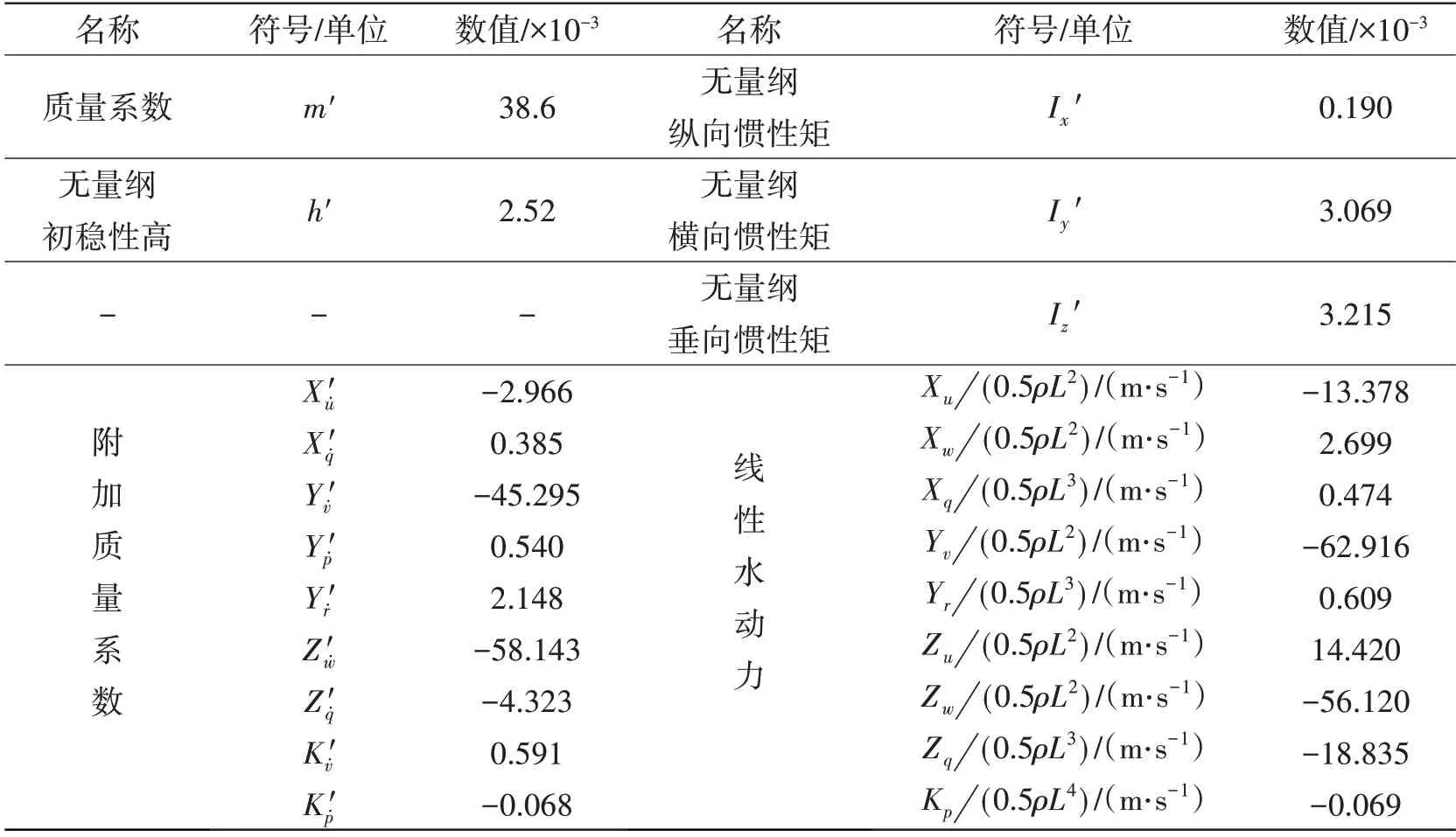
表1 深海作業平臺相關參數Tab.1 Related parameters of deep-sea work platform

續表1

3.2 結果分析

載荷和運動的表達均采用潛艇操縱性研究中的坐標系。大地坐標系為慣性坐標系，隨體坐標系為非慣性坐標系，X軸指向平臺艏部，Y軸指向平臺右舷，Z軸可按右手系確定。原點位于深海作業平臺的質心處。

3.2.1 單周期正弦載荷下的運動

單周期正弦載荷在大地坐標系下的表達式為

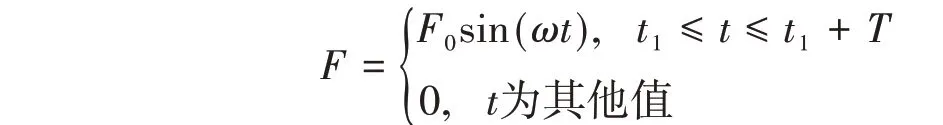
假設作用力方向豎直向下，作用點距質心的縱向距離為l。大地坐標系下，干擾力可表達為

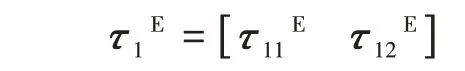
取F0=0.001 89m，l=0.106L，ω取0.1 rad/s。圖1給出了無海流的情況下考慮和不考慮剛體質量科氏力時平臺在單周期正弦載荷作用下的擾動仿真結果。從圖1 可以看出，考慮剛體質量科氏力與不考慮剛體質量科氏力，對于不加控制措施的開環仿真結果是有區別的，在該算例中縱向速度和縱向位移的擾動結果差異最明顯。顯然，從水動力角度出發，動力定位數學模型中剛體質量科氏力不應該被忽略。

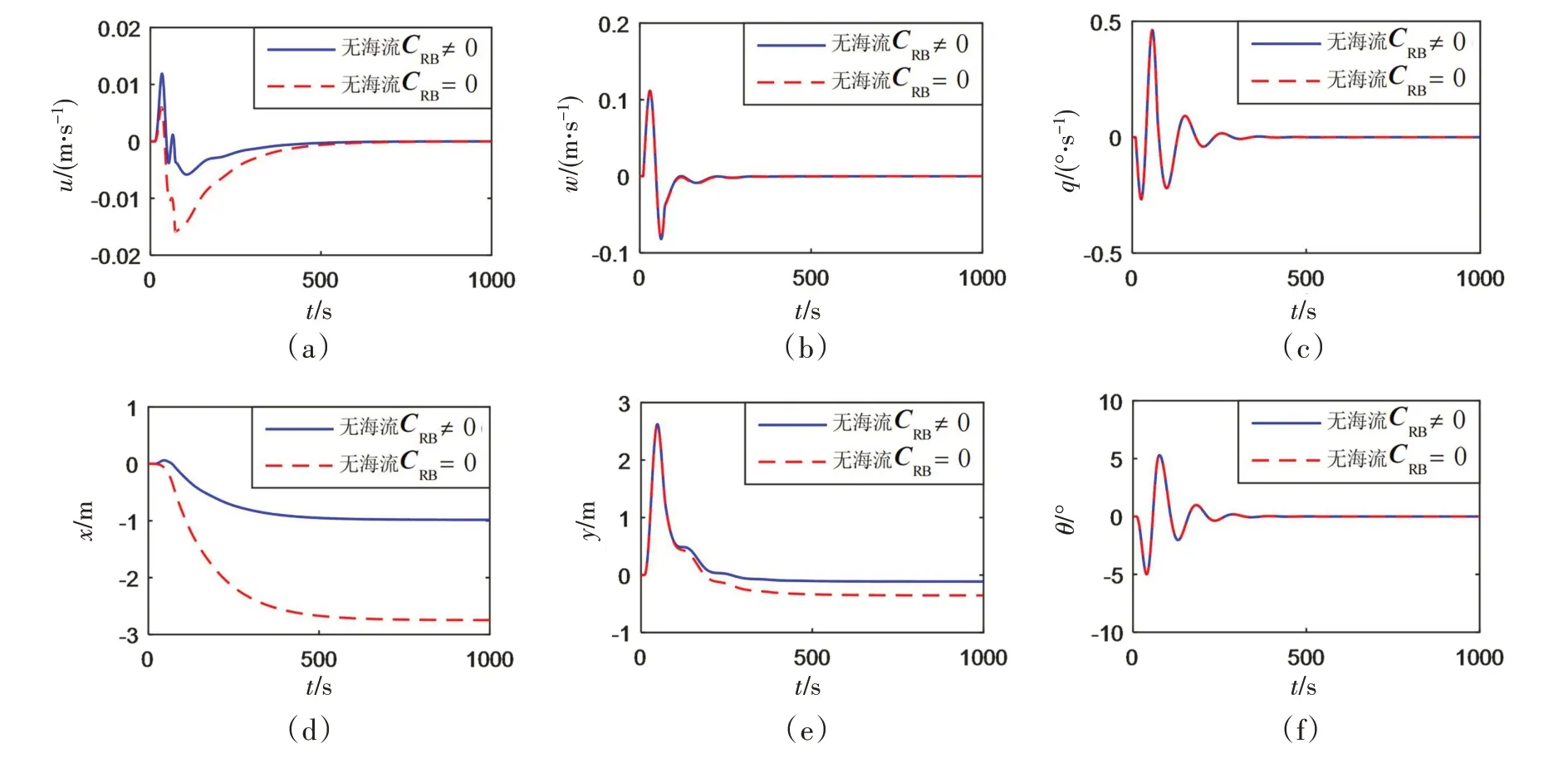
圖1 無海流工況下考慮或不考慮剛體質量科氏力時平臺擾動仿真結果比較Fig.1 Comparison of simulation results with or without the Coriolis force of rigid body mass under no ocean currents case

圖2 給出了有無海流狀態下平臺在單周期正弦載荷作用下的擾動仿真結果。從圖2 的結果可以看出，動力定位數學模型在考慮海流載荷平衡后的擾動結果與無海流狀態下的擾動結果接近。其中細微的差別主要是因為，擾動產生后平臺縱傾姿態變化導致海流載荷的變化，因此擾動過程中平衡初始狀態海流載荷的推力無法平衡擾動后的海流載荷，這與完全無海流的絕對平衡狀態是有區別的。從圖2可以看出，這種區別較小，在垂向單周期正弦載荷作用的情況下可忽略。

圖2 單周期正弦力作用下有無海流情況下平臺擾動仿真結果比較Fig.2 Comparison of simulation results with and without ocean currents under a single-cycle sine force

3.2.2 脈沖力載荷下的運動

取脈沖力載荷可視為平臺在布放潛器、與潛器協同作業過程中可能受到的纜繩傳遞給平臺的脈沖力。在大地坐標系下脈沖作用力表達為定義脈沖力在大地坐標系下的方向：與水平面的夾角為αF，與垂直面的夾角為βF。假設脈沖力作用點距質心的縱向距離為l，大地坐標系下干擾力表達為

取F0=0.189m，l=0.106L，αF=60°，βF=30°，脈沖力可分解出三個方向的分量，平臺六個自由度均會出現較明顯的擾動。有無海流狀態下，擾動仿真結果的對比見圖3和圖4。

圖3 有海流與無海流狀態脈沖力作用下擾動仿真結果比較Fig.3 Comparison of simulation results with and without ocean currents under impulse force

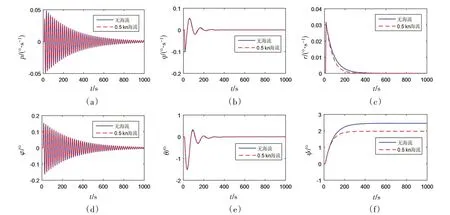
圖4 有海流與無海流狀態脈沖力作用下擾動仿真結果比較Fig.4 Comparison of simulation results with and without ocean current under impulse force

從圖3和圖4這兩圖的比較可以看出，橫向速度和橫向位移出現了較大區別。平臺橫傾角和縱傾角在靜扶正力矩的作用下最終恢復至零位。但偏航角一旦產生，就無法恢復，從而較大地改變了原本的迎流平衡狀態。偏航角產生后，迎流阻力中出現橫向阻力分量，進而形成橫向速度，不斷產生橫向位移。在沒有橫向推力輸出進行控制的情況下，橫向位移將一直增大，因此出現圖3（e）中橫向位移持續增大的情況。垂向位移出現的偏差主要是迎流平衡在脈沖力作用下被破壞后平臺速度上形成微小差異累積后形成的位移差異。

從以上的研究可以看出，如果擾動主要出現在垂直面內，那么在迎流平衡的基礎上，可近似采用無海流情況的擾動結果取代有海流情況下的擾動結果。當考慮六自由度擾動定位時，原有的迎流平衡狀態因偏航角無法恢復至零而被改變，有海流情況的擾動結果不能近似采用無海流的擾動結果，應直接采用動力定位數學模型對有海流工況進行仿真計算。

4 結 論

本文通過深海作業平臺動力定位中水動力問題的分析，建立了深海作業平臺動力定位數學模型，明確了該模型的基準平衡狀態為迎流平衡的原地懸停狀態，并建議數學模型中水動力系數可采用原地或微速狀態下振蕩運動來計算，利用該數學模型對懸停迎流狀態下某平臺在單周期正弦載荷和脈沖載荷干擾下產生的擾動仿真進行了初步研究。通過研究分析，得到了如下結論：

（1）剛體質量科氏力項對仿真結果有影響，建議數學模型中不要忽略。

（2）在很多水面和水下平臺的動力定位控制研究文獻中，將附加質量科氏力也考慮在內，這可能是不合適的，因為目前傳統的水池模型試驗已經將這一部分力考慮在水動力阻尼項中了，因此附加質量科氏力是否選用需要根據水動力實際獲取方法進行分析處理。

（3）對于有海流情況，垂直面內的擾動問題可以用無海流狀態下的擾動結果來近似，而六自由度空間擾動問題則必須對考慮海流的數學模型進行仿真分析。

目前的數學模型還未考慮多推進器布局下推力的作用，這涉及到一定的槳槳干擾和平臺與槳的相互干擾問題，并與多推進器的具體布局密切相關，后續還需要根據這一部分的研究完善數學模型。