例談高中數學不等式的教學策略

夏琴

【摘 要】 在高中數學教材中，不等式占據著非常重要的地位，是學生面臨的較難學習內容之一，同時在數學高考中也占據比較重要的部分.從實際的教學活動角度來看，教師在對學生進行不等式教學的時候會感覺比較吃力.因為不等式具有較強的邏輯性，學生在進行課程知識學習的時候不容易掌握和控制;不等式是學生高中數學學習中較難的一部分，加之高中教學氛圍相對來說比較壓抑，所以對學生的整體學習上還是會有一定的影響.因此，在實際的課堂教學環境中，如何做好不等式的教學工作，需要數學教師不斷分析和探討.本文立足高中數學課程的教學現狀，結合數學高考試題對不等式教學進行分析和探究.

【關鍵詞】 數學課程;高中數學;高考試題

作為高中數學授課教師來說，我們在進行課程教學活動的時候，應該對自己所授課的內容有一個正確認知，只有做好這一方面的工作，才能夠在實際的教學活動中，切實有效推動學生的數學學科核心素養發展.而對于高中數學不等式來說，它屬于數學基礎理論知識中比較重要的一部分，其中所涉及到的內容，實際上也與學生日常生活息息相關.

高中數學不等式實際上就是現實世界不等關系的數學模型，也是進行數量關系研究的必由之路，因此，不等式教學在當前高中數學課程中占據相當重要的地位.

在新課程改革中，針對不等式教學方面，教師應該結合好實際課程的教學要求，通過發揮學生的學習主動性和主體性，實現更好的數學教學效果和學生素養發展.

1 高考試題中對于不等式的考查分析

對于高中數學教師來說，為了切實做好對學生的不等式教學工作，需要知道在當前的高考試題中，針對不等式這一方面是如何進行設置的.通過對這一方面內容的了解，并對高考試題類型形成一個較為明確的了解和把握[1].由此才能在實際的學習情境和教學工作中，加強對學生的數學教學.

通過筆者的調查研究能夠知道，在目前的高考試題中，不等式可以說是高考的重點以及熱點，其考查點會從函數和實踐應用兩個方面入手，并以此為背景，考查學生的數學基礎知識與基本技能，還會考核學生的邏輯推理能力、測試運算能力以及分析問題和解決問題的能力.

仔細分析近年高考試題可以發現，關于不等式的考查多為綜合性試題：選擇題和填空題的不等式解集以求最值為主，解答題大多為不等式與函數數列導數結合的綜合試題，客觀題主要考查線性規劃與不等式的解法.也就是說，不等式的考查一般會融合進其他題型中，并不進行單獨命題，分值為10分左右.雖然這些題目的廣度和深入有所提升，但主要是考查學生對不等關系的感受、建立與處理，而性質闡述與證明推導的技巧其實已是降低.

總體而言，高考試題關于不等式的考查還是比較全面的，能夠從多個角度、多種題型來考查學生，指引并引導學生對問題進行思考，促進學生數學思維邏輯能力的形成[2].

2 高中數學中不等式教學的方式

高中數學教師立足于高考試卷分析的基礎上，需要對高中數學課程中不等式教學的具體工作展開相應的分析和探討，從而找到合適的教學方式，以此來切實有效的推動學生的數學成績的提升與發展.因此，在接下來的論述中，筆者將對這一方面的問題說出自己的想法和觀點.

2.1 結合生活內容展開教學活動

教師在高中數學課堂教學中落實不等式教學活動的時候，可以結合生活內容來給學生展開教學活動.無論是對于哪一個階段的學生來說，生活中的知識內容往往是學生最熟悉的知識內容，也是學生最能夠融入投入理解的.尤其是到了高中階段，結合好生活知識來給學生落實開展相應的教學工作.

一方面能夠在課堂上幫助學生緩解一定的學習壓力，讓學生能夠在實際的學習環境中，切實有效的投入到教師所設計的各種環節之中，形成對課程知識的了解與體會.

另一方面能夠給到學生不一樣的學習體驗，為學生構建一個相對來說比較輕松活潑的課堂，以此推動整體課堂學習上的提升與發展.

例如 針對這一方面的教學活動來說，教師可以給學生講解以下題目：“限速40km/h的路面，司機在行駛的時候，速度v應該不超過40km/h，用不等式如何進行表達？”針對這一道題來說，它是直接采用了學生平時在生活中常常能夠看到的場景和畫面，并以這一畫面為出發點，從而來給學生展開具體的知識構建和探究活動.

教師在講解的時候，可以適當的將這個題目的生活化內容進行放大.具體來說，教師可以利用多媒體視頻的方式來給學生演示這一方面的知識內容，以此來實現學生對于整體知識上的提升與整合，從而切實有效地促進學生的核心素養發展.

2.2 注重對不等式解法的講解

在高中數學課程教學工作中，教師面對不等式教學工作的時候，需要注重對不等式解法的講解.從教師教學工作本身的實際內容來看，其中最重要的一點，就是要幫助學生掌握相應知識的解答方式.

通過筆者的調查研究工作能夠發現在當前的高中數學課程教學當中，教師在給學生進行不等式教學的時候，會給學生展開講解解法，但是解法講解的方式相對來說比較乏味和枯燥，這樣學生就無法在實際的學習環境中獲得相應的提升與發展，導致學生在聽講的過程中，無法做到專心致志，由此會對學生的解題思路以及具體能力都會形成一定的影響.

作為教師來說，我們在給學生進行不等式，減法講解的時候，不僅要有所側重，而且還要有策略，這樣一來才能夠在實際的教學環境中，有效地推動學生解題能力的發展.

教師在給學生進行不等式解法的講解時，可以加強對不等式與方程、三角、函數、數列等這些方面的之間的聯系.通過將這些內容聯系起來，能夠讓學生在實際的學習工作中，形成較為綜合、立體的知識框架，促進學生整體知識學習上的提升與知識結構的發展.

2.3 加強給學生的邏輯推理，促進學生思維的發展

對于高中數學教師來說，教師在給學生進行不等式教學的時候，要加強對學生的邏輯推理教學，以此促進學生思維上的發展.在前面的分析和論述中，我們已經交代過不等式教學，實際提高對學生的思維邏輯非常有作用的，并且能夠讓學生在一定的程度上，推動自身數學解題思維能力的提升與發展.

如何才能夠在實際的課堂教學中，切實有效地給學生做好這一點，這是需要教師認真分析的問題.在相關調查和研究工作中，筆者發現，教師想要在不等式教學工作中實現提升學生的邏輯、推理，促進學生的思維發展，就需要構建趣味情境.

所謂的構建趣味情境，實際上就是教師在給學生進行課堂教學設計的時候，采用一些比較活潑有趣的教學方式，以此來達到一個相對來說比較有趣的教學環境.這樣才能夠在實際的教學環境中，推動學生對于整體知識學習上的提升與發展，切實有效地打動學生，讓學生能夠更好地掌握不單是這一方面的工作[3].

例如 以“限速40km/h的路面，司機在行駛的時候，速度v應該不超過40km/h，用不等式如何進行表達？”這一教學為例，在這一道題目中，教師要引導學生對內容進行分析和思考.

具體來說，教師可以利用任務化視頻解題分析的形式來展開.具體來說，將這一道題目變成闖關題，每一個有效的條件，都是學生完成一定的關卡從而才能夠獲得.最后通完全關，學生自然也獲得了對知識的體會和答案.

通過這樣的方式，一方面能夠讓學生在實際學習的環境中，進一步形成字對于課程知識的思考與體會，另一方面能夠然學生感受到數學課程知識學習的樂趣，切實有效的推動學生獲得成長與發展，達到一個良好的課堂教學效果.

2.4 采用真題及時進行教學訓練

高中數學教師講解不等式時，還需要采用真題來及時進行教學訓練，既然在實際的課堂教學中教師想要讓學生能夠在高考環境下，切實有效地實現自我學習，那么教師就需要給高中學生一個相對來說比較真實且完整的情境，這樣一來學生才能夠在實際的環境中提升自己的解題能力和解題意識，從而促進自身的發展，讓學生在真正面臨高考的時候，也能夠做到應對自如.

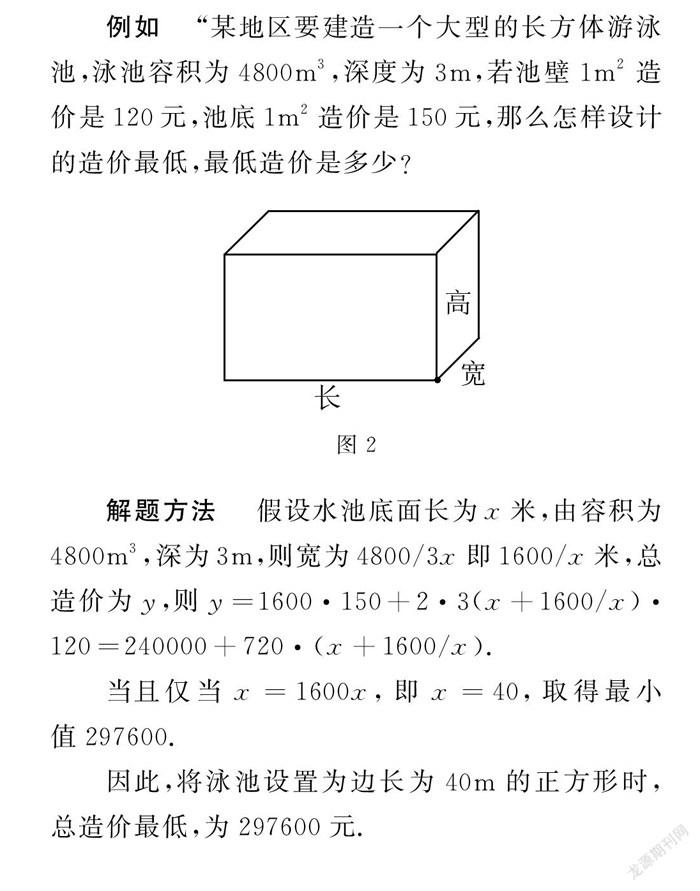
例如 “某地區要建造一個大型的長方體游泳池，泳池容積為4800m3，深度為3m，若池壁1m2造價是120元，池底1m2造價是150元，那么怎樣設計的造價最低，最低造價是多少？

解題方法 假設水池底面長為x米，由容積為4800m3，深為3m，則寬為4800/3x即1600/x米，總造價為y，則y=1600·150+2·3（x+1600/x）·120=240000+720·（x+1600/x）.

當且僅當x=1600x，即x=40，取得最小值297600.

因此，將泳池設置為邊長為40m的正方形時，總造價最低，為297600元.

這一題教學為例，教師在進行具體教學的時候，可以先讓學生結合前期教師所教學的內容，嘗試進行自我解題上的應用.

通過具體的應用，讓學生能夠了解相關的知識內容.然后教師再結合學生的表達進行具體的知識整合和分析工作.通過這樣的真題訓練形式來加強學生對于課程知識的掌握和體會.

高中數學課堂教學中，教師落實好不等式教學工作是非常重要的，如何才能有效地落實好這一方面的工作，需要教師從學生的整體發展以及對高考真題的分析、研究兩方面入手，通過綜合這兩方面的不同要求，開展好相關的教育教學工作.這樣才能夠在最為直接和實際的課堂環境中，引導學生牢固掌握相關的知識內容，有效推動學生獲得自我學習意識和學習能力的提升，從而整體推進學生個體數學學科核心素養的發展[4].

參考文獻：

[1]瞿志彬.新課改下關于高中數學不等式高考試題分析與教學策略研究[J].課程教育研究：外語學法教法研究，2019，（22）：122-123.

[2]孔令華.策略分析，優化提升——高中數學不等式高考試題分析與教學策略研究[J].數學大世界（下旬），2018（7）：78-79.

[3]白鳳娟.高中數學不等式高考試題分析及教學策略研究[J].數學學習與研究，2014，（11）：32-32.

[4]郭志宏.基于高考試題的高中數學不等式教學研究[J].數學學習與研究，2017（7）：136-136.

[5]張海強.基于“大概念”的高中數學教學探索——以“基本不等式的綜合運用”為例[J].江蘇教育.2020（75）

[6]傅海倫，張晗，劉亞男.促進學生深度學習的教學案例與分析——以《基本不等式》為例[J].中學數學雜志.2021（11）

[7]黃清鈿.引導學生深度學習數學的階梯式題組教學初探——以高中數學新教材“2.2基本不等式”一節為例[J].福建基礎教育研究.2021（11）

[8]王富英，黃芳.對話講解是培養學生數學核心素養的有效途徑——以基本不等式求最值的教學為例[J].教育科學論壇.2017（34）