基于參考點位移邊界條件的千斤頂卸載及頂升模擬方法

焦常科

上海建工集團股份有限公司 上海 200080

千斤頂廣泛應用于大跨空間結構或者結構體系轉換時的頂升或卸載[1]中。在有限元計算模型中，等效模擬需要實現的特性包括：千斤頂的位移變形特性，千斤頂下的臨時支撐結構回彈或進一步壓縮，千斤頂與結構支承點脫開或再接觸。千斤頂在有限元計算模型中，常見的處理方法包括：將臨時支撐及千斤頂簡化為支座，對支座分階段施加強制位移[2]；等效桿端位移法是將臨時支撐等效為具有相同軸向線剛度的彈性桿，采用只能受壓單元來模擬彈性桿，通過給彈性桿下端支座施加豎向強迫位移來模擬千斤頂的下降[3]；千斤頂單元法，將主體結構與臨時支撐同時建在模型中，并在兩者之間采用只壓單元來模擬真實的千斤頂，將千斤頂單元的軸向剛度設為無窮大，采用施加溫度荷載的方法控制千斤頂單元的軸向變形[4]。

蔣金生等[5]基于Ansys平臺采用強制位移法對上海新國際博覽中心鋼桁架結構卸載過程進行分析，計算結果與實測值除局部點最大偏差21%外，其余吻合較好。

常樂等[6]在對跨度120 m的大同美術館鋼結構屋蓋施工卸載模擬時，同步與非同步豎向卸載分別采用強制位移和刪除支撐胎架實現。

本文從廣義約束方程出發，通過引入參考點的邊界條件實現千斤頂的頂升或卸載特性。以懸臂梁端部的卸載和頂升為例，將計算結果與理論值進行對比，以說明本文所述方法的正確性。

1 基本原理

有限元模型邊界條件處理時，經常會使用耦合方程以在實現若干節點的某些自由度之間形成選定的約束關系，約束方程一般格式如式（1）所示。

在千斤頂上端設置只受壓單元模擬千斤頂與結構支承點脫開或再接觸特性，千斤頂卸載或頂升的模擬等效示意如圖1所示。

圖1 千斤頂等效示意

上述方法可以通過參考點的反力獲得千斤頂在進行位移調整過程中的內力變化。基本思路如下：

1）選定千斤頂軸線所在方向，記為z方向，對應的節點自由度為3。

2）假定被支承結構的支承點以及臨時支撐點分別為T和B。

3）假定千斤頂的頂、底位置對應的節點分別為P和Q，引入參照節點為R。

4）建立只受壓單元，分別連接第1節點C和第2節點M，該單元僅在選定方向z進行力與位移的傳遞；該單元的抗拉剛度為0，受壓剛度為最大值。

5）被支承結構支承點T與只受壓單元的第1節點C僅在選定方向z上進行力與位移的傳遞；千斤頂的頂面對應節點P與只受壓單元的第2節點M僅在選定方向z上進行力與位移的傳遞；千斤頂的底面對應節點Q與臨時支撐點B僅在選定方向z上進行力與位移的傳遞。

6）在節點P、Q和R之間，建立如式（3）所示的約束方程：

7）假定千斤頂的頂、底面對應的節點P和Q，在選定方向z上需產生的相對位移為f(u,t)；對參考節點R在方向z上施加位移邊界，對應值為f(u,t)；同時，R節點其他自由度設置固定約束，避免節點R在該自由度上出現剛體位移。

2 單點支撐卸載

以端部設有彈性支承的懸臂梁在均布荷載作用下的力學特性為例，說明溫度調節法的基本應用。

懸臂梁為a×b的矩形截面，長L，彈性模量為E；臨時支撐長度為l，圓形截面直徑為D，彈性模量同懸臂梁，如圖2所示。

圖2 懸臂梁基本模型

根據力學方法計算得到懸臂梁端部支撐的內力如式（4）所示，相應的端部變形如式（5）所示。

懸臂梁無端部支撐時的豎向位移如式（6）所示，慣性矩的計算如式（7）所示。

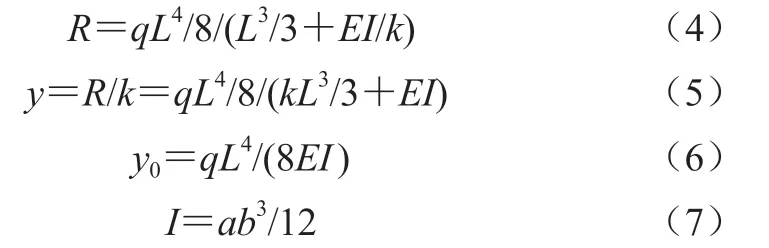
式中：k—懸臂梁端部支撐線剛度，k＝EA/l＝πD2E/(4l)。

選定基本參數值具體如下：E＝2.1×105MPa，a＝50 mm，b＝100 mm，L＝2 m，l＝800 mm，D＝8 mm，q＝20 N/mm。經計算，懸臂梁端部位移及支撐內力分別為y＝－1.109 mm、R＝14.636 kN，相應的固定端豎向反力為25.346 kN；相應無端部支撐時，y0＝45.71 mm。可見：端部支持如完全卸載，臨時支撐結構彈性回彈量為1.109 mm；端部卸載量達到45.71 mm時，可達到完全卸載狀態。

作為對比，采用溫度調節法，將千斤頂等效為彈性模量極大的單個構件，對其施加負溫度荷載以達到卸載的目的。將臨時支撐上端千斤頂等效為直徑6 mm、長100 mm的圓柱，假定其彈性模量E＝2.1×107MPa、線膨脹系數α＝0.01，則對應的溫度變化量為ΔT＝－45.71 ℃。

建立平面有限元分析模型，分析步包括：均載q作用；溫度調節法中，千斤頂等效單元降溫ΔT＝－45.71 ℃，參考點位移法中，對參考點施加豎向位移－45.71 mm；溫度調節法中，千斤頂等效單元降溫ΔT＝－50.0 ℃，參考點位移法中，對參考點施加豎向位移至－50 mm。

計算結果對比如圖3所示。

圖3 懸臂梁結構卸載響應

由圖3可見，2種模擬方法的結果基本完全一致：在step1中，梁端位移即臨時支撐壓縮彈性變形為－1.113 mm，與理論值（－1.109 mm）偏差僅0.34%，如圖3（a）所示；相應的臨時支撐內力計算值為14.54 kN，與理論值（14.636 kN）偏差僅0.66%，如圖3（b）所示；在step2中，梁端位移計算值為－45.75 mm，與理論值（－45.71 mm）偏差僅0.09%；相應的臨時支撐的壓縮變形完全回彈至0，反力全部釋放，如圖3（c）、圖3（d）所示；在step3中，千斤頂繼續卸載并與梁端脫開，此時懸臂梁端部位移固定為－45.75 mm，只受壓單元進入受拉階段，相應的臨時支撐反力為0，懸臂梁固定端豎向反力維持極值（40 kN）不變，如圖3（a）、圖3（b）所示。

3 單點支撐頂升

根據懸臂梁端部受集中荷載下的撓度公式，懸臂端部發生位移y時，相應的集中力如式（8）所示。

在上述算例基礎上，調整分析步為：均載q作用；對參考點施加豎向位移25 mm；對參考點施加豎向位移至50 mm。計算結果如圖4所示。

圖4 懸臂梁頂升響應

由圖4可見：在step1中，懸臂梁端部撓度及臨時支撐反力和固定端反力與理論計算一致；在step2中，千斤頂的上下端面發生25 mm的伸長變形，臨時支撐發生0.606 mm（1.719－1.113＝0.606 mm）壓縮變形；千斤頂上端及懸臂梁端變形增量為24.293 mm（23.28＋1.113＝24.293 mm），相應臨時支撐軸力增量為7.993 kN（22.684－14.691＝7.993 kN），與懸臂梁固定端反力減少量7.933 kN（25.309－17.316＝7.933 kN）吻合，與按式（8）的理論計算結果（8.004 kN）一致；在step3中，千斤頂的上下端面伸長變形繼續增大至50 mm，臨時支撐總的壓縮變形增加至－2.325 mm，懸臂梁端變形增至47.675 mm；相應的懸臂梁固定端反力繼續減少，荷載轉移至臨時支撐上。

由上述分析可見，本文所述模擬方法可準確實現千斤頂的頂升過程模擬。

4 結語

本文從廣義約束方程出發，通過引入參考點的邊界條件實現千斤頂的頂升或卸載特性。以懸臂梁端部的卸載和頂升為例，將計算結果與理論值對比以說明本文所述方法的正確性。計算結果與理論值對比表明，本方法可真實再現千斤頂的卸載及頂升特性，可在有限元模型建模過程中用于對千斤頂特性進行模擬。