熱改性粉煤灰對水中銅的動態吸附研究

駱欣 ，劉瑞森 ，徐東耀 ，葉錦莎

（1. 中國礦業大學（北京）化學與環境工程學院，北京 100083；2. 華北科技學院化學與環境工程學院，北京 101601；3. 華北科技學院安全工程學院，北京 101601）

我國是煤炭資源大國，煤炭是我國的主體能源。粉煤灰是燃煤產生的固體廢棄物，排放量大且逐年遞增，是我國最大的單一固體污染源[1]。粉煤灰的資源化利用成為當今的主要問題。作為一種低成本的吸附劑，粉煤灰被廣泛應用于水處理領域[2-3]。原粉煤灰（FA）的吸附能力較低，因此常采用物理、化學等方法對粉煤灰進行改性，以增強其吸附能力，如微波/堿FA、堿FA、酸FA 和鹽FA[4]。不同類型的改性粉煤灰吸附劑已被用于去除廢水中的重金屬離子[5-6]。銅是水體中常見的重金屬污染物，具有來源廣、毒性大、易累積、難生物降解等特點[7]。在前期的研究中，將粉煤灰進行熱改性，并用于靜態吸附水中的銅[8]。與其他工業固廢吸附劑和粉煤灰改性吸附劑相比，熱改性粉煤灰顯示了對Cu2+良好的吸附效果。此外，熱改性操作簡單，改性劑價格低廉[9]，又避免了酸、堿等改性方法可能帶來的二次污染，因此具有良好的工業應用前景。在工業化應用中，吸附過程一般屬于連續流動性操作。為了模擬實際工程應用，本文采用固定床吸附實驗，研究不同條件下出水Cu2+濃度隨時間的變化，并結合三種動態吸附模型對吸附數據進行擬合，用于評估熱改性粉煤灰對Cu2+的動態吸附行為。

1 實 驗

1.1 材料和儀器

粉煤灰產自唐山某燃煤電廠，化學藥品碳酸鈉、硝酸銅、硝酸鉛、硝酸鋅均為分析純，實驗用水為去離子水。

馬弗爐，XL-1 型；原子吸收分光光度計，GGX-600 型，；X-射線衍射儀，D8 ADVANCE 型。

1.2 實驗方法

（1）粉煤灰的熱改性。將粉煤灰過0.25 mm篩，用去離子水清洗、烘干。取12 g 預處理后的粉煤灰（FA）與4 g 無水Na2CO3充分混合，置于馬弗爐中，在800℃下活化2 h。冷卻、研磨后過0.18 mm 篩，即得所需的改性粉煤灰（MFA）。

（2）動態吸附實驗。在直徑1.1 cm、高20 cm的吸附柱中加入一定量的MFA。吸附柱的上端填充1 cm 高的0.43～0.85 mm 石英砂，使溶液分布均勻。吸附柱的下端同樣填充石英砂作為承托層。采用蠕動泵控制Cu2+溶液自上而下流經吸附床的速度。每隔一段時間測定出水中Cu2+的質量濃度。定義出水濃度（ct）達到進水濃度（c0）0.1 的時間為穿透時間（tb），ct/c0為0.9 對應的時間為耗竭時間（te）。

1.3 分析方法

Cu2+質量濃度由火焰原子吸收法測定，波長為324.7 nm。Cu2+的動態吸附容量（qe, mg/g）和吸附率（η, %）分別用式（1）、（2）計算。

式中，c0和ct（mg/L）為t（min）時Cu2+進、出口濃度，Q（mL/min）為流量，m（g）是MFA 的質量，te（min）為耗竭時間。

2 結果與討論

2.1 動態吸附的影響因素

2.1.1 床層高度

表1 為MFA 動態吸附Cu2+的參數。圖1 為不同床層高度下的吸附穿透曲線。由圖1 可知，隨著床層高度由5 cm 增加至9 cm，Cu2+的穿透時間由33 min 延長至133 min，吸附容量由1.84 mg/g增至2.04 mg/g。隨著床層高度的增加，Cu2+與MFA 的接觸時間增加，柱內液體分布增強，溶質在吸附劑之間的擴散度越高，吸附過程越充分[10]。床層高度越大，MFA 質量相應增加，Cu2+的吸附位點增多，因此吸附效率也越高。由表1可知，當床層高度為9 cm 時，吸附效率增至67.45%。此外，穿透曲線的斜率與床層高度呈負相關，表明突破是漸進的。

表1 MFA 對Cu2+的動態吸附參數Table 1 Dynamic adsorption parameters of Cu2+ on MFA

圖1 不同層高下Cu2+的穿透曲線Fig.1 Breakthrough curves of Cu2+ under different bed heights

2.1.2 流量

圖2 顯示了不同流量對MFA 吸附Cu2+的影響。穿透時間隨著流量的增加而顯著減小。當流量增加到4 mL/min 時，吸附床很快被穿透，穿透時間縮短至26 min。低流量下，穿透曲線更加平緩，傳質范圍變寬，有利于Cu2+的吸附去除[11]。在較高的流量下，溶液在吸附床中的停留時間減小，Cu2+與MFA 的接觸時間縮短，導致Cu2+的吸附容量和吸附效率均有所下降。當流量為4 mL/min時，Cu2+的吸附容量和吸附率分別降至1.27 mg/g和63.81%。

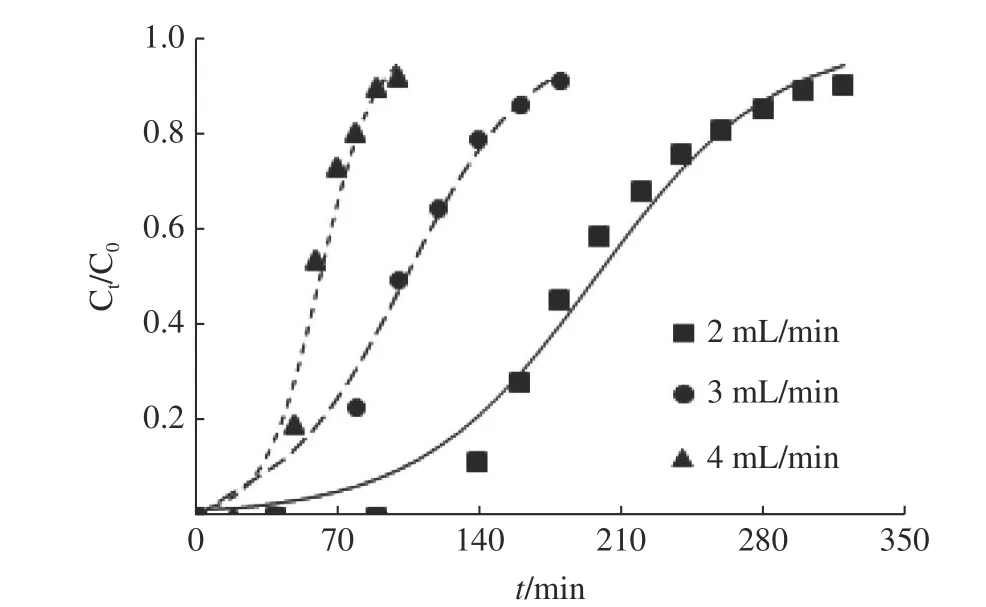
圖2 不同流量下Cu2+的穿透曲線Fig.2 Breakthrough curves of Cu2+ under different flow rates

2.1.3 溶液初始濃度

Cu2+的初始濃度為10、20 和30 mg/L 對應的穿透曲線見圖3。由圖3 可知，隨著Cu2+初始濃度的增加，吸附劑被更多的Cu2+包圍，MFA 表面的吸附位點被更快地占據，吸附床很快飽和，因而穿透時間變短，穿透曲線逐漸向左偏移。由于吸附位點的數量有限，當Cu2+濃度由10 mg/L 增加到30 mg/L 時，吸附效率降低了9.03%。然而，隨著初始濃度的升高，Cu2+在溶液和吸附劑之間的濃度梯度增加，吸附驅動力增大[12]，吸附量qe值相應增加了0.5 倍。

圖3 不同初始濃度下Cu2+的穿透曲線Fig.3 Breakthrough curves of Cu2+ under different initial concentrations

2.2 動態吸附的模型擬合

2.2.1 Thomas 模型

Thomas 模型假設吸附平衡符合Langmuir 等溫線和二級反應動力學[13]，數學形式如下：

式中，kT（mL/(min·mg)）為速率常數，qe（mg/g）為吸附容量。

采用Thomas 模型對動態吸附過程進行擬合，擬合參數見表2。由表2 可知，在不同的實驗條件下，Thomas 模型的相關系數（R2）在0.92～0.98之間，模型預測的吸附容量（qe）與穿透曲線的計算值（qe,exp）接近，表明Thomas 模型可以較好地描述Cu2+在MFA 上的動態吸附。當床層高度由5 cm 增加到9 cm 時，速率常數（kT）由1.97 mL/(min·mg)降至1.15 mL/(min·mg)，表明軸向分散和質量傳輸阻力有所增加[14]。在高流量下，吸附質的流動性增強，傳質阻力降低，kT值增大。當流量增至4 mL/min 時，kT值增加到3.69 mL/(min·mg)。隨著Cu2+初始濃度的增加，kT值減小至0.86 mL/(min·mg)，這是由于較高的吸附質濃度會引起傳質系數有所減小[13]。

表2 Thomas 模型的擬合參數Table 2 Parameters of Thomas model under different conditions

2.2.2 Yoon-Nelson 模型

Yoon-Nelson 模型形式簡單，不需要吸附質和吸附劑的詳細資料，可用于預測表示吸附速率的τ值[15]，表達式為：

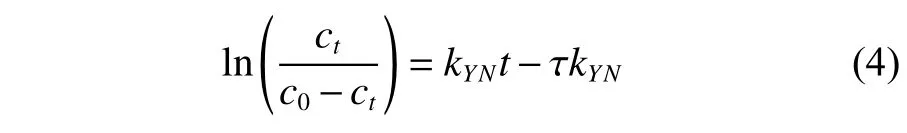
式中，kYN（1/min）為Yoon-Nelson速率常數，τ（min）為ct/c0為0.5 時需要的時間。

Yoon-Nelson 模型與Thomas 模型在數學上是等價的，因此R2值也在0.92～0.98 之間。由表3可以看出，該模型得到的τ與實驗數據吻合較好，表明Yoon-Nelson 模型可以預測動態吸附曲線。速率常數KYN隨床層高度的增加而減小，隨流量和Cu2+初始濃度的增加而增大。床層高度的增加會導致傳質阻力增大，傳質速率降低，因而KYN減小。提高流量有利于傳質性能的改善，增高Cu2+初始濃度使得傳質推動力增強，傳質速率均會增加，KYN值增大。

表3 Yoon-Nelson 模型的擬合參數Table 3 Parameters of Yoon-Nelson model under different conditions

2.2.3 Adams-Bohart 模型

基于表面反應理論的Adams-Bohart 模型假設平衡不是瞬時的，吸附速率與吸附劑的剩余吸附容量及吸附質濃度成正比[10]，見式（5）。

式中，N0為單位體積的飽和吸附量（mg/L），kAB為Adams-Bohart 速率常數（L/（mg·min）），Z為床層高度（cm），F為空床速度（cm/min）。

穿透曲線的N0、kAB以及R2見表4。Adams-Bohart 模型的R2值在0.70～0.83 之間，表明擬合效果比Thomas 和Yoon-Nelson 模型差。由表4 可知，Bohart-Adam 速率系數（kAB）隨床層高度和Cu2+初始濃度的增加而減小，隨進水流量的增加而增大。這歸因于kAB的變化取決于表面擴散系數的變化[16]。N0代表體積飽和吸附量，與Thomas 模型參數qe類似，隨著初始濃度的升高和進水流量的下降，呈現出相似的變化趨勢。然而N0值隨著床層高度的增加變化不顯著，可見Cu2+的動態吸附過程主要發生在MFA 固定床的上層[17]。

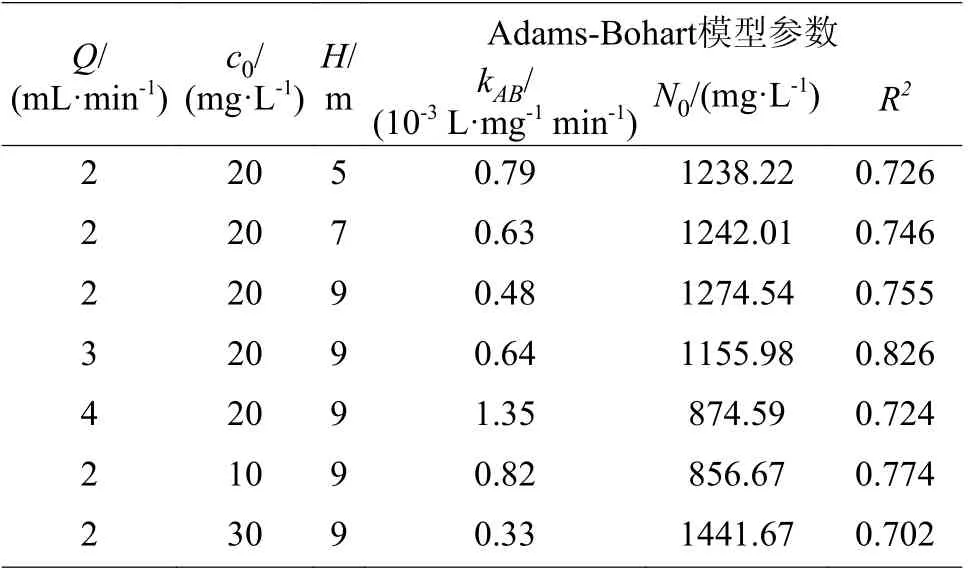
表4 Adams-Bohart 模型的擬合參數Table 4 Parameters of Adams-Bohart model under different conditions

2.3 XRD 分析

為進一步了解MFA 吸附Cu2+的機理，在前期FTIR 分析的基礎上[8]，對FA、吸附Cu2+前后的MFA 進行了XRD 測定，見圖4。根據Jade6.0軟件分析，FA 的主要礦物相為硅線石(Silimanite,Al2(SiO4)O)、石英(Quartz, SiO2)和赤鐵礦(Hematite, Fe2O3)等結構。FA 經熱處理后，原有的玻璃網格結構被破壞，生成了鈉霞石(Nepheline,NaAlSiO4)、針鐵礦(Goethite, FeO(OH))、白云石(Dolomite, MgCa(CO3)2)等新物質。吸附Cu2+后，NaAlSiO4、FeO(OH)、MgCa(CO3)2晶體的衍射峰的位置未見偏移，但峰的強度有所增強，表明溶液中Cu2+與鈉、鐵或鈣鎂晶體之間存在離子交換作用[17]。結合MFA 吸附前后的FTIR[8]，可知MFA 吸附Cu2+的機制主要包括O—H 等含氧官能團與Cu2+的絡合反應、Cu2+與Na+等陽離子發生的離子交換。

圖4 FA 和MFA 吸附Cu2+的XRDFig.4 XRD spectra of FA and Cu2+ adsorbed on MFA

2.4 Zn2+、Pb2+的競爭吸附

在吸附床高度9 cm、流量2 mL/min、Cu2+初始濃度 20 mg/L 的條件下，考察了Zn2+和Pb2+對Cu2+吸附性能的影響，見圖5。對穿透曲線進行三種動態吸附模型的擬合，發現Adams-Bohart模型不能預測雙組分混合物中Cu2+的吸附（R2＜0.8），而Thomas 模型和Yoon-Nelson 模型可以較好地擬合雙組分體系中Cu2+的穿透曲線（R2：0.92～0.94）。Thomas 模型預測的吸附容量（qe）與穿透曲線計算的吸附容量接近。與單組分溶液相比，雙組分體系中Cu2+的吸附耗竭時間和吸附容量均減小，反映了金屬離子間的吸附競爭。Pb2+比Zn2+呈現出更強的抑制作用，表明Pb2+對MFA 具有較高的親和力。三種金屬離子的水合離子半徑順序依次為Pb2+（4.01）＜Cu2+（4.19）＜Zn2+（4.30），水合半徑越小的金屬離子空間位阻越小，越容易接近活性吸附位[18]。與Cu2+和Zn2+

圖5 雙組分體系中Cu2+的吸附穿透曲線Fig.5 The breakthrough curves of Cu2+ in the binary system

相較，Pb2+的共價指數更高[19]，與O 原子中的孤對電子有更強的相互作用而形成絡合物[20]。

2.5 吸附劑的損失

表5 顯示了雙組分體系中Cu2+的三個動態吸附模型擬合參數。在動態吸附過程中，吸附劑由于受到水流的持續沖刷會造成一定的質量損失。因此，在吸附床高度為9 cm、進水為去離子水的條件下，考察了不同流量下MFA 的損失率隨時間的變化，見圖6。由圖6 可知，隨著時間的延長，MFA 的損失率逐漸增加。120 min 后損失率趨于平穩，流量為2、3、4 mL/min 對應的損失率分別為0.38%、0.52%、0.72%，較低的損失率表明MFA 是一種比較耐水力沖刷的吸附劑。

表5 雙組分體系中Cu2+的動態吸附模型擬合參數Table 5 Parameters of different models in the binary system

圖6 MFA 損失率隨時間的變化曲線Fig.6 The change curves of mass loss rate with time

3 結 論

（1）在熱改性粉煤灰對Cu2+的動態吸附中，床層高度、流量以及Cu2+初始濃度均會影響穿透時間和吸附效率。增加床層高度，Cu2+的穿透時間延長，動態吸附能力增強。提高流量和初始濃度，Cu2+的穿透速率加快，動態吸附率降低。

（2）采用Thomas、Yoon-Nelson 和Adams-Bohart 模型對動態吸附數據進行擬合，吸附過程符合Thomas 和Yoon-Nelson 模型。降低床層高度、增加流量和初始濃度，有助于提高動態吸附速率。

（3）在雙組分體系中，Zn2+和Pb2+的存在均會抑制MFA 對Cu2+的動態吸附，抑制性表現為Pb2+＞ Zn2+。