基于無跡卡爾曼濾波的無刷直流電動機無位置傳感器控制

馬相如，楊澤斌

(1.國網漣水縣供電公司，淮安 223400；2. 江蘇大學 電氣信息工程學院，鎮江 212013)

0 引 言

無刷直流電動機(以下簡稱BLDCM)的傳統位置傳感器控制方法，增加了硬件成本和體積，且位置傳感器易受電磁信號、粉塵等干擾，使得控制性能下降。目前BLDCM常用的無位置傳感器控制方法包括反電動勢法、磁鏈觀測法、續流二極管導通檢測法、擴展卡爾曼濾波法等，其中擴展卡爾曼濾波法是卡爾曼濾波在非線性系統中的擴展，其利用較容易獲得的電壓、電流信號，結合BLDCM狀態方程，實現對轉子位置和轉速信號的觀測，具有魯棒性好、調速范圍寬等優點，是目前BLDCM無位置傳感器控制研究的熱點。但是這種方法是通過泰勒展開式逼近非線性函數，由于僅保留到一階精度，觀測到的轉速和轉子位置信號誤差較大[1-2]。

為了提高擴展卡爾曼濾波器觀測的精度，本文提出了一種改進的無跡卡爾曼濾波(以下簡稱UKF)算法，相較于擴展卡爾曼濾波算法，可有效提升估算精度。UKF沒有忽略高階項，最低可達到非線性函數的二階精度，因此具有更高的估算精度。本文將其應用于BLDCM轉速和轉子位置觀測中，實現了BLDCM無傳感器控制[3-4]，仿真和實驗結果證實了理論分析的正確性。

1 BLDCM數學模型

本文的BLDCM為三相星形連接，采用全橋逆變器驅動、兩兩導通方式，其連接示意圖如圖1所示。

圖1 BLDCM連接示意圖

理想情況下，BLDCM電壓方程如下：

(1)

式中：ua、ub、uc，ia、ib、ic，ea、eb、ec分別為定子繞組相電壓，相電流，反電動勢；R、L、M分別為每相繞組電阻、自感和相間互感。

BLDCM電磁轉矩方程如下：

(2)

式中：ω是角速度。

BLDCM運動方程如下：

(3)

式中:J、Bv、Tl分別為轉動慣量、摩擦系數和負載轉矩。

2 UKF算法原理

2.1 卡爾曼濾波算法分析

卡爾曼濾波器結構如圖2所示，其采用遞歸方法在考慮外部干擾的情況下仍然能夠獲得最優估測值，并且便于數字化實現，在導航制導、信號處理等領域應用廣泛。

圖2 卡爾曼濾波器系統結構圖

卡爾曼濾波器工作原理如下：控制系統的狀態變量同時輸入至系統模型和卡爾曼濾波器模型，系統模型估測值與卡爾曼濾波器模型估測值作差后，由卡爾曼濾波器模型估測出最優值，再將其反饋至卡爾曼濾波器模型，通過不斷遞推與迭代，最終估計值收斂于接近真實值的范圍。

系統的狀態方程和量測方程如下：

(4)

式中：x(k)為系統狀態向量；Φ(k+1,k)為轉移矩陣；H(k)為測量矩陣；w(k)和v(k)分別為系統本身和測量過程中的干擾信號。

w(k)和v(k)的統計特性如下：

(5)

系統初值的統計特性如下：

(6)

(7)

根據上面的結果求出卡爾曼濾波增益Kk：

(8)

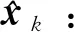
(9)

最后計算迭代過程所用最優估測方差矩陣Pk：

Pk=Pk/k-1-KkHkPk/k-1

以上的卡爾曼濾波算法分析是基于線性模型，而實際系統多為非線性模型，為了彌補卡爾曼濾波算法不適應非線性系統的缺陷，提出擴展卡爾曼濾波算法(以下簡稱EKF)，先對非線性系統線性化變換，再作離散化處理。然而，傳統EKF方法在對非線性系統方程進行線性化處理時，只具有泰勒級數的一階精度，導致誤差較大。在實際應用中，需要對EKF方法進一步優化。以確定性采樣為思路，Julier等學者進一步將無跡變換與EKF算法相結合，提出了UKF算法，它具有更高的估測精度。

2.2 無跡變換

對于任意非線性系統，其非線性函數可用下式表示：

y=f(x)

(10)

無跡變換[5-6]過程如下：

首先，選取合適的Sigma點χi，實際選擇過程中可參考下式：

(11)

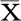
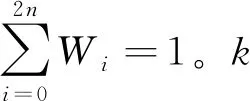
其次，對2n+1個Sigma點作非線性傳播，如下：

yi=f(χi) (i=0,…,2n)

(12)

計算可得：

(13)

2.3 UKF算法原理

UKF算法主要利用比例無跡變換替換EKF算法中的雅克比矩陣，從而實現非線性系統的線性化變換，其遞推過程主要包括4個步驟[7-8]。假設存在某非線性系統，離散化表示如下式：

(14)

式中：xk代表系統狀態向量；uk代表輸入向量；σk、μk代表相互獨立的高斯白噪聲，且滿足下式關系：

(15)

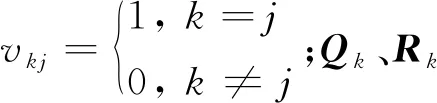
第一步初始化。計算初始狀態統計特性如下式：

(16)

(17)

第二步采樣。根據Sigma點的選取規則，取2n+1個Sigma點，并計算其權值：

(18)

第三步時間更新。利用非線性狀態函數f(·)對采樣中所得Sigma點作非線性傳播，如下：

(19)

進而可得：

(20)

(21)

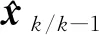
(22)

式中:α值通常在0.000 1～1內，β值通常等于2。

(23)

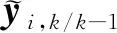
(24)

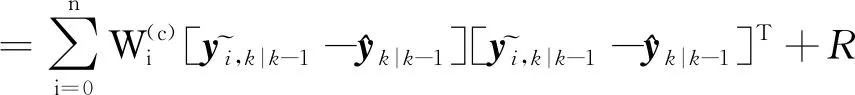
(25)

(26)

進一步可得：

(27)

式中：Kk代表濾波增益矩陣。

根據新的測量yk即可進行量測更新：

(28)

(29)

3 UKF在BLDCM中的應用

BLDCM非線性數學模型如下：

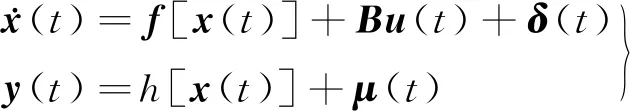
(30)

式中：x(t)代表狀態變量；u(t)、y(t)分別代表輸入、輸出變量；δ(t)代表系統擾動、轉速波動、參數誤差等所有系統噪聲；μ(t)代表測量噪聲。

各變量方程如下：

為了將本文研究的UKF算法運用到BLDCM控制中，需進一步對BLDCM系統方程作離散化處理，結果如下：

(31)

根據上式，結合前文分析的UKF原理，可得基于UKF算法的BLDCM無傳感器算法實現流程，如圖3所示[9-10]。

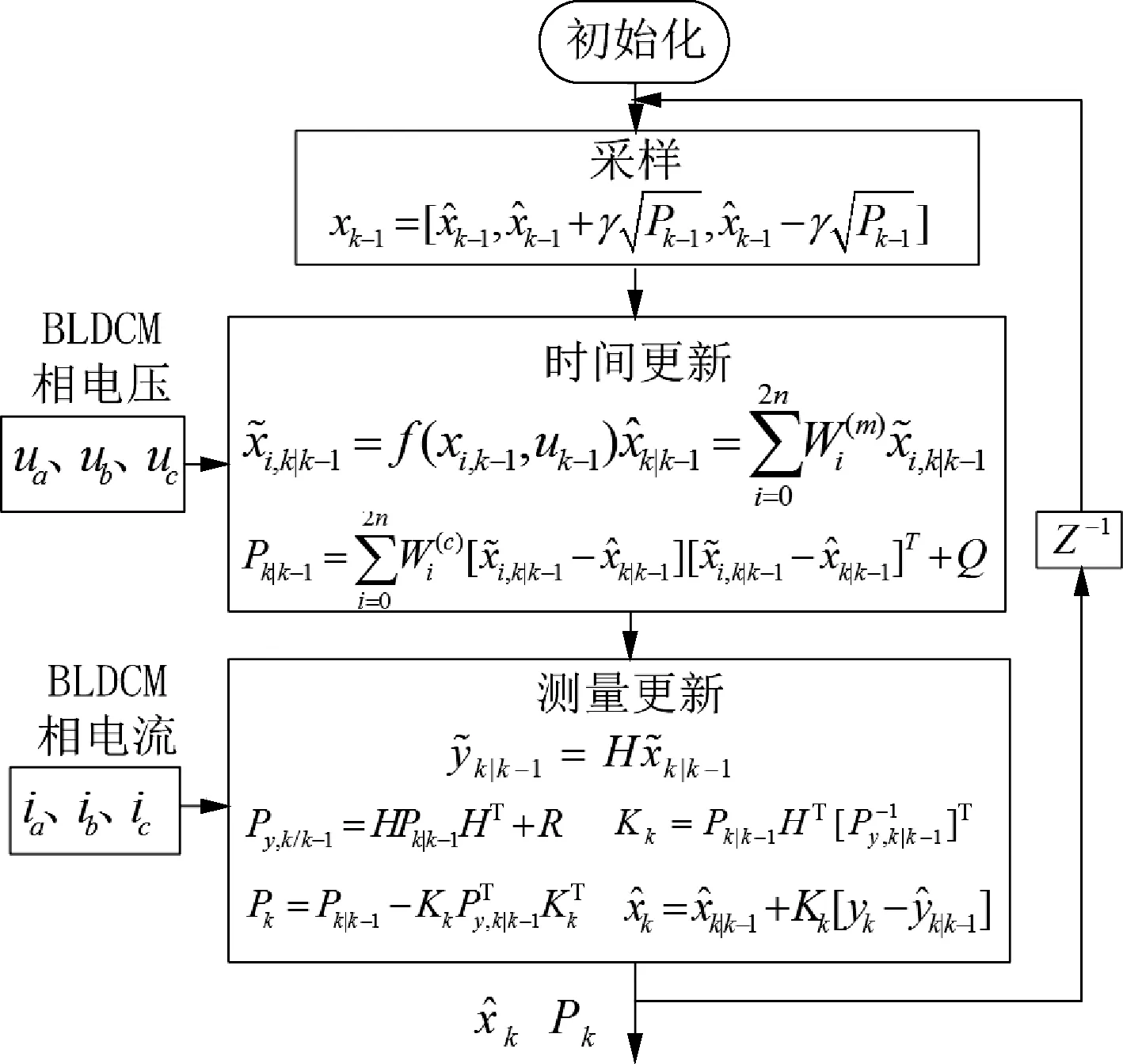
圖3 UKF算法實現流程圖

進一步可得BLDCM基于UKF算法的無位置傳感器、雙閉環控制結構框圖[11-12]，如圖4所示。

圖4 BLDCM基于UKF算法的雙閉環控制

控制系統采用無跡卡爾曼濾波器觀測得出轉速和轉子位置信號，并將其應用于BLDCM轉速、電流雙閉環控制中。

4 仿真分析

利用MATLAB軟件自帶的S函數功能模塊編寫UKF算法，并嵌入到模型中，搭建MATLAB仿真模型，BLDCM仿真參數如表1所示。

表1 仿真參數

針對不同轉速、轉速發生突變、負載發生擾動三種情況進行仿真。

4.1 不同轉速下仿真分析

當BLDCM給定轉速分別為2 000 r/min和200 r/min時，UKF觀測與實際測量的轉速和轉子位置分別如圖5、圖6所示。需要說明的是UKF算法得到的轉子位置信號是連續的角度，在BLDCM驅動控制中還需要對其進行轉換，轉換原理如圖7所示。

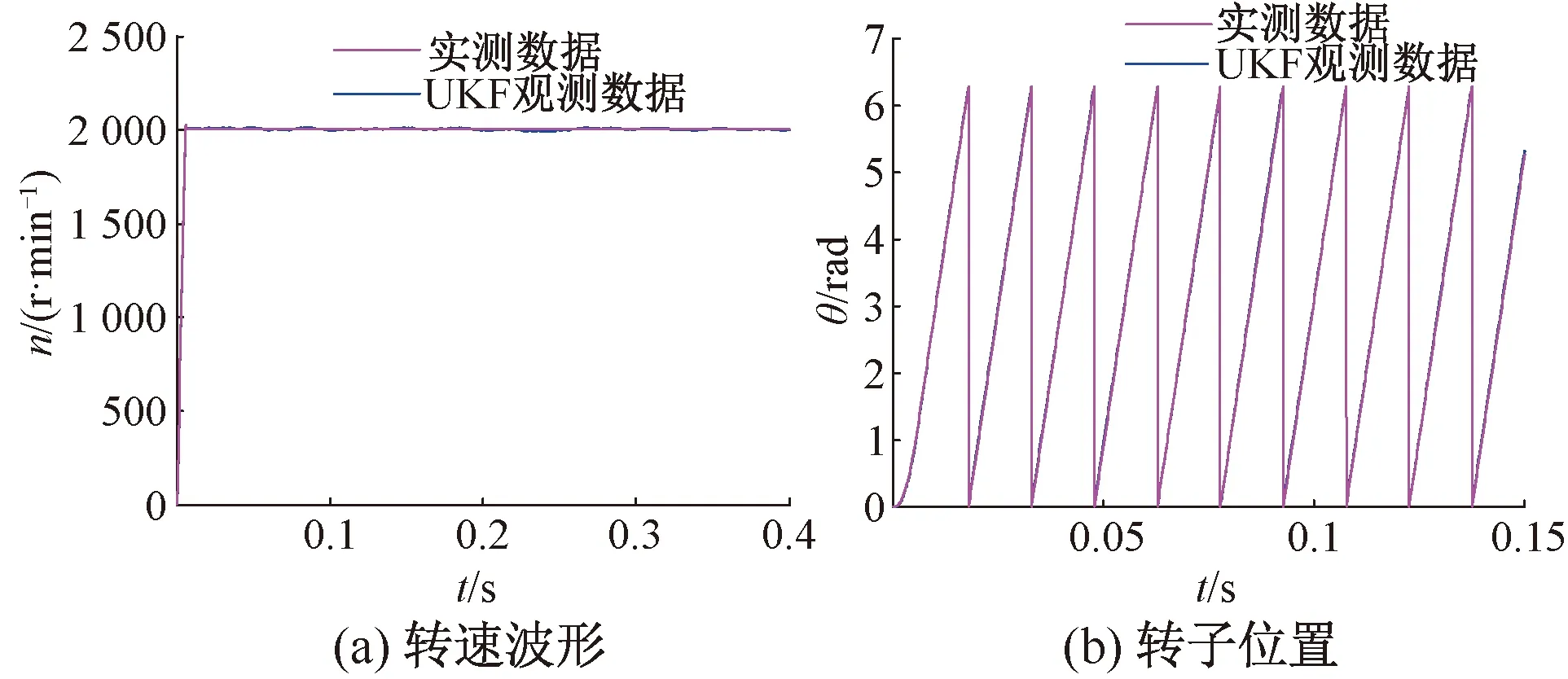
圖5 給定轉速為2 000 r/min時仿真結果

圖6 給定轉速為200 r/min時仿真結果

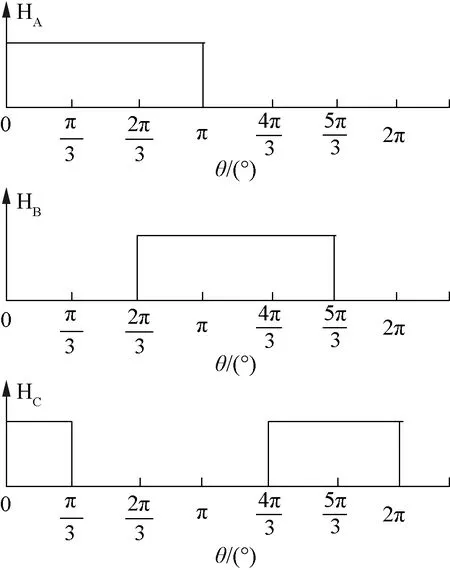
圖7 UKF算法獲取轉子位置轉換原理

由圖5、圖6可見，高、低速情況下UKF觀測與實際測量的轉速和轉子位置之間誤差較小，且高速時的觀測精度優于低速情況。

4.2 轉速發生突變時仿真分析

初始狀態下BLDCM給定轉速為1 500 r/min，0.1 s時轉速突增至2 000 r/min，UKF觀測與實際測量的轉速和轉子位置如圖8所示。

圖8 轉速發生突變時的仿真結果

由圖8可見，轉速發生突變時UKF觀測器仍能夠準確觀測轉速和轉子位置，觀測精度較高，與實際測量值之間誤差較小，動態觀測效果良好。

4.3 負載發生擾動時的仿真分析

初始狀態下負載轉矩為0.66 N·m，0.1 s時負載轉矩開始增大，0.15 s時達到最大值0.96 N·m，之后逐漸恢復至0.66 N·m，UKF觀測與實際測量的轉速和轉子位置如圖9所示。

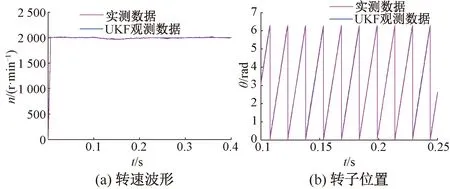
圖9 負載發生擾動時的仿真結果

由圖9可見，當負載轉矩發生擾動時，UKF算法仍然能夠準確觀測轉速和轉子位置，具有較好的抗負載擾動能力。可見，UKF算法可以實現BLDCM高、低速無位置傳感器控制，且在轉速發生突變、負載發生擾動等情況下，仍然能夠準確觀測轉速和轉子位置，具有較好的動、靜態性能及觀測精度。

5 實驗研究

為進一步驗證理論分析的正確性，基于DSP28335+FPGA的控制器結構進行實驗驗證，實驗現場接線如圖10所示。

圖10 實驗接線圖

實驗主程序、定時器中斷子程序及捕獲單元中斷子程序流程圖如圖11所示。

實驗所用BLDCM參數與仿真參數一致，BLDCM空載起動過程中電壓、電流波形如圖12所示。

由圖12可見，由于電機電感、換相及小功率BLDCM齒槽效應等原因，空載狀態下電流波形并不是理想的方波。

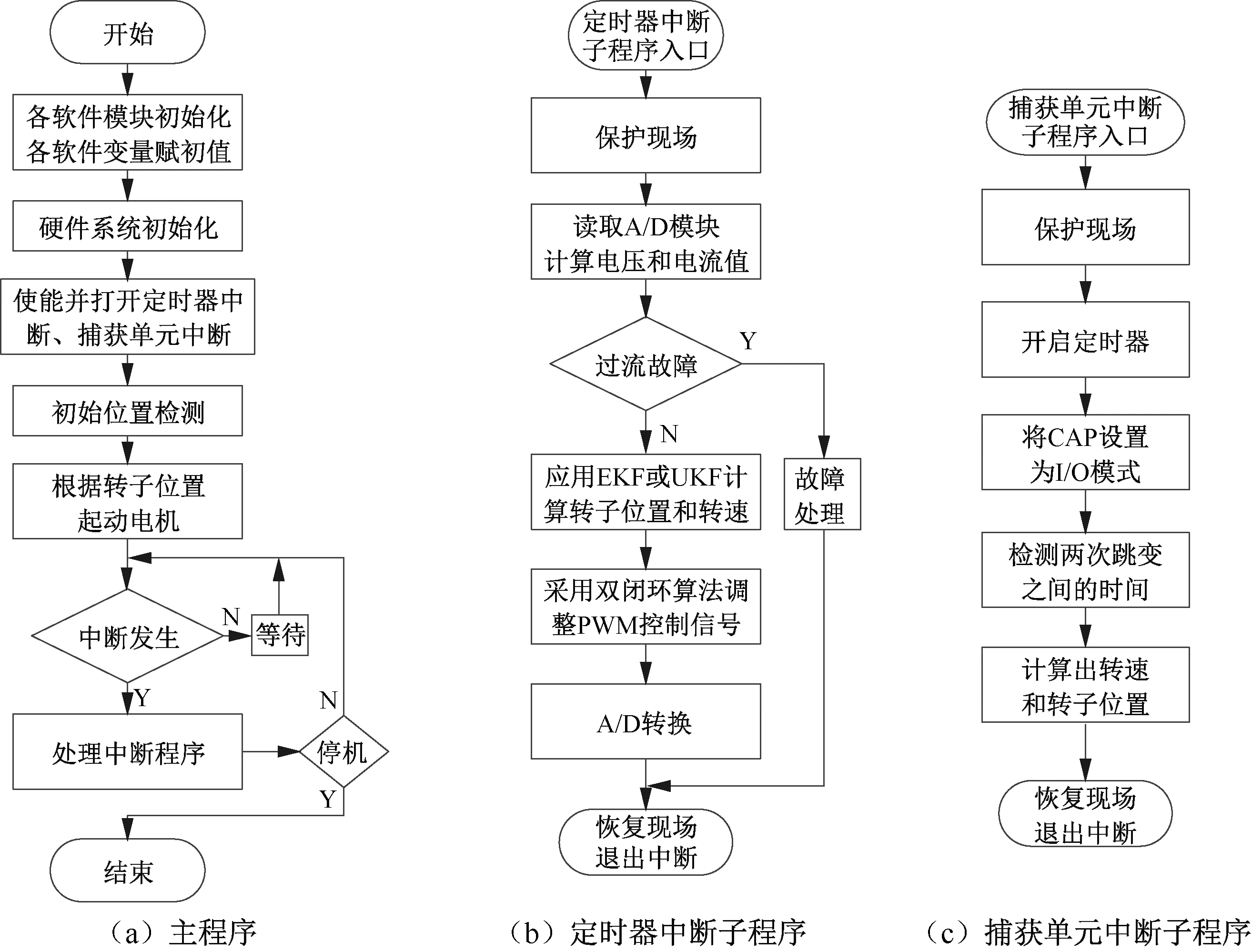
圖11 程序流程圖

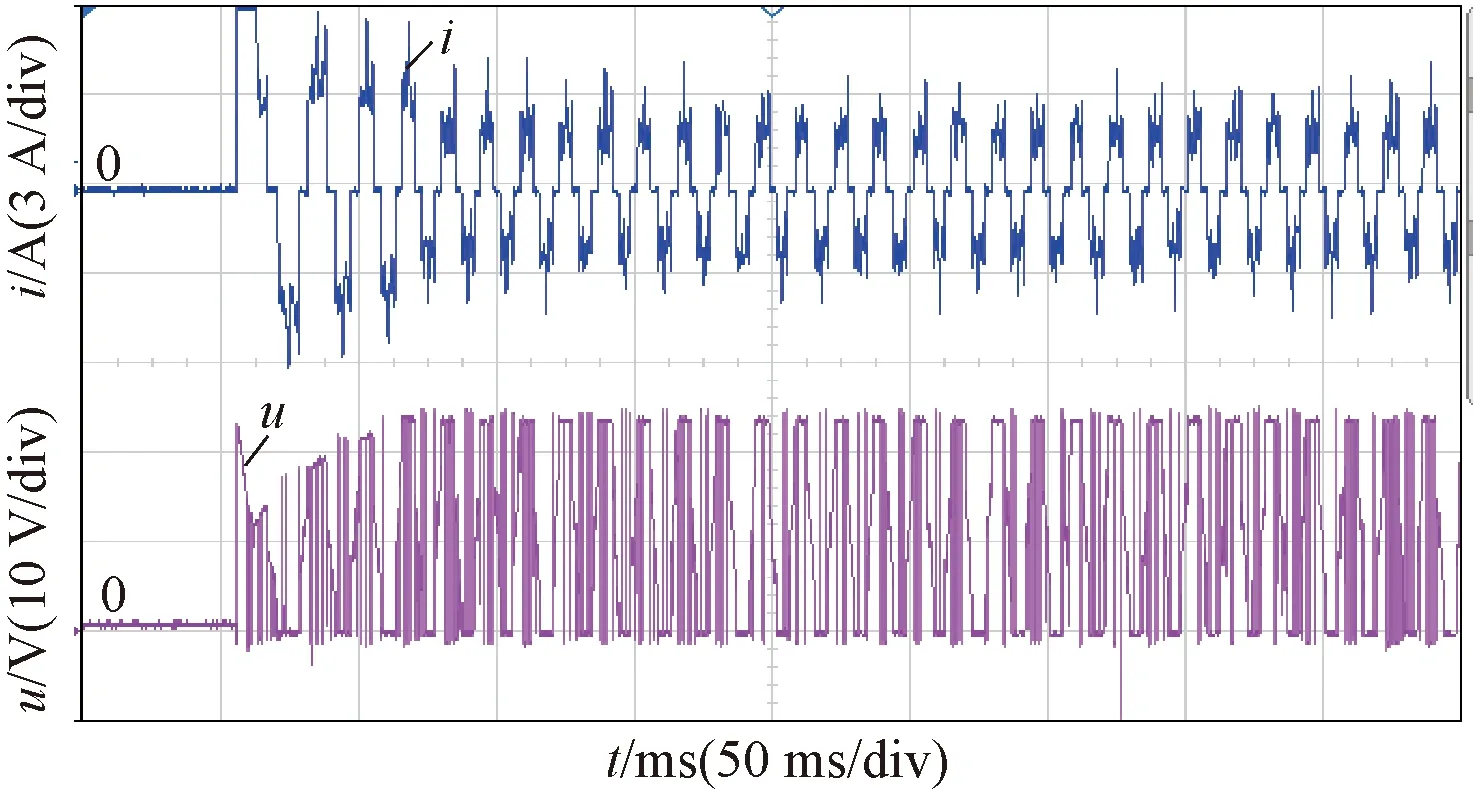
圖12 BLDCM電壓、電流波形

為了比較UKF估測的轉子位置與實際轉子位置間差異，本文同時采用霍爾傳感器進行實測。然而霍爾傳感器輸出信號并不是連續的角度，而UKF輸出信號是連續的角度，難以直接對比。因此，本文按照圖7的霍爾傳感器輸出脈沖信號與轉子位置之間關系對UKF輸出結果進行轉換。

當BLDCM轉速分別為200 r/min、2 000 r/min時，霍爾傳感器實測轉子位置信號與UKF觀測轉子位置信號轉換后波形如圖13所示。

圖13 轉子位置測量結果

由圖13可見，無論BLDCM工作在高速或者低速狀態，UKF算法觀測的轉子位置與霍爾位置傳感器測量結果基本一致，二者之間誤差較小，可見UKF算法具有較高的轉子位置觀測精度。

在DSP28335中UKF觀測的轉速信號和實際轉速信號均為數字量，若采用示波器顯示，則需要將其轉化成模擬信號，而在數模轉換過程中會受到噪聲干擾等產生誤差，影響判斷結果。為了避免此問題，本文將UKF觀測的轉速和實際轉速分別存放在兩個變量中，再通過MATLAB繪制出來進行分析。

當BLDCM給定轉速分別為2 000 r/min、200 r/min時，UKF觀測轉速與實際轉速如圖14所示，由于轉速是根據CCS中數組變量繪制而來，圖中橫坐標是數組變量的下標值。

圖14 實際轉速與UFK觀測轉速

由圖14可見，在高、低速情況下BLDCM起動初期UKF算法觀測轉速與實際轉速之間存在一定誤差，經過短暫收斂后，轉速趨于穩定，UKF算法觀測轉速與實測轉速基本一致，誤差較小。

當給定轉速由1 000 r/min增至2 000 r/min時，UKF觀測轉速與實際轉速如圖15所示。

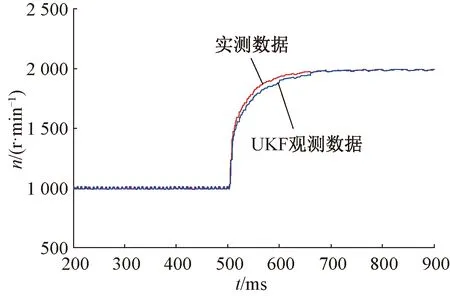
圖15 轉速突變時實際轉速與測量轉速

由圖15可見，當給定轉速參考值發生突變時，UKF算法仍可以準確跟蹤并觀測轉速，且與實際測量值之間誤差較小。

由以上實驗結果可見，基于UKF算法的BLDCM無位置傳感器控制方法具有良好的動、靜態性能，能夠有效提高BLDCM轉速、轉子位置的觀測精度，具有一定的推廣應用價值。

6 結 語

針對擴展卡爾曼濾波器算法觀測精度不夠高的問題，本文提出了一種改進的UKF算法。相較于EKF算法，UKF算法可有效提升估算精度，將其應用于BLDCM無位置傳感器控制中，理論證明UKF算法至少可以達到非線性函數的二階精度。仿真和實驗結果表明，UKF算法在BLDCM高、低速運行情況下，均可以準確觀測轉速和轉子位置，并且在轉速、負載轉矩發生突變時，仍然能夠準確跟蹤觀測，具有較好的動、靜態性能和觀測精度。