基于可觀測性分析的機載SINS起飛階段自標定研究

趙 陽，戴邵武，丁 祥，楊大光，戴洪德

(1.海軍航空大學 岸防兵學院, 山東 煙臺 264001； 2.海軍航空大學 航空基礎學院, 山東 煙臺 264001)

1 引言

慣性導航系統是一種具有抗干擾能力強、隱蔽性好等特點的自主導航系統，在軍工和民用等多個領域有著廣泛的應用。但是在長時間工作后，系統內部的慣性測量單元(inertial measurement unit,IMU)參數受到環境等外部因素的影響，會發生變化，從而導致慣性導航系統精度逐漸下降。因此對系統內部的參數進行估計和補償，即對系統進行標定，是保證機載慣導系統性能的一項重要工作。

為了保證機載SINS的導航精度，我國機載SINS的傳統標定方法主要是基于精密轉臺的實驗室定期標定，有六位置法和十二位置法等。這種標定方式過程繁瑣，耗費大量的人力、物力和時間，同時在拆裝和轉運過程中還可能引入新的誤差，存在標定周期長、成本高、影響部隊的日常維護和戰機的快速反應等缺點。為了便于維護、實現視情標定，提高長期穩定性，結合免拆卸標定的需求，提升戰機的快速機動性，本文對機載SINS的空中標定進行深入研究。

在進行空中標定前，有必要對系統進行可觀測性分析。可觀測性與誤差項能否被激勵，進而成功被估計出來緊密相關，一般以可觀測度定義捷聯慣導系統誤差項在機動方式下能否被激勵。

當系統模型為線性時變系統模型時，直接進行可觀測性分析，需要計算Grammian矩陣，計算量過大且不利于實際分析。以色列學者Goshen-Meskin等將系統拆為多個分段線性定常系統(piece-wise constant system，PWCS)進行可觀測性分析，很大程度上減少了計算量，但這個方法僅能對系統可觀測性進行定性判斷，不能對系統中各個狀態量進行可觀測性分析，同時也無法定量分析各狀態變量的可觀測程度。東南大學的程向紅等在上述理論基礎上，提出對可觀測性矩陣進行奇異值分解(singular value decomposition,SVD)，實現了對系統可觀測性的定量分析。陸志東提出了一種針對機載捷聯式系統的空中標定方法，實現了SINS部分參數的標定，但是未對各種路徑進行可觀測性分析。Wu等根據全局可觀測性對捷聯慣導系統可觀測性進行分析，且對里程計輔助的車載捷聯慣導系統進行可觀測性分析，但未考慮IMU的標度因數誤差。夏宇強對常規機動下的組合導航可觀測性進行分析，在機載慣導標定時具有一定參考價值，但未考慮IMU標度因數誤差，且在仿真驗證時，必要的機動動作有所缺失。同時上述方法均存在衛星導航精度無法保證等問題。

針對上述問題，本文提出一種基于可觀測性分析的機載SINS起飛階段自標定方法。從系統狀態可觀測性分析出發，采用基于PWCS的奇異值分解方法，對飛機做不同機動時，各狀態變量可觀測度進行分析比較，找出不同的機動條件對各狀態變量的激勵效果。據此設計了一種充分利用機場附近差分GPS和起飛時機動條件的飛行軌跡。最后對3種基于不同觀測量的慣導起飛階段自標定分別進行仿真分析，驗證了上述標定方法和結論的有效性，并得出基于速度匹配的自標定模型標定效果較好的結論，最后將本文提出的基于可觀測性分析設計的飛起軌跡與基于常規起飛軌跡的空中標定算法進行了仿真分析，進一步驗證了本文標定方法的有效性，為空中自標定系統模型選擇和飛行軌跡的設計提供理論依據和應用參考，具有一定的實際意義。

2 慣導自標定系統濾波模型設計

2.1 IMU測量誤差模型

慣性器件的輸出精度主要受到陀螺儀的常值漂移誤差、標度因數誤差和加速度計的零偏影響，假設安裝誤差為小量，且在定期標定周期內被認為是不變的。加速度計的測量誤差模型為：

(1)

陀螺儀的測量誤差模型為：

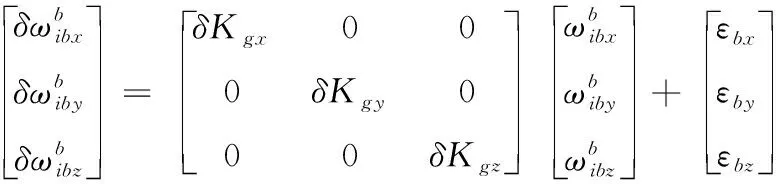
(2)

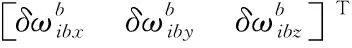
2.2 起飛階段自標定原理分析

慣導起飛階段自標定方法依據系統級標定的思想，將機場附近差分GPS等外部高精度基準信息和慣導解算輸出的導航信息之差作為系統的外部觀測信息，根據可觀測性分析設計飛行機動條件和軌跡，激勵出各誤差項，利用Kalman濾波實現待標定參數估計，從而對系統誤差進行補償，以此來提高導航精度，確保機載SINS性能的長期穩定性。

2.3 狀態模型

自標定模型將姿態、速度、位置誤差方程及陀螺儀和加速度計的常值誤差、標度因數誤差方程作為整個系統的狀態方程，表達式為：

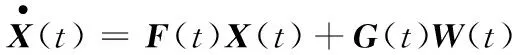
(3)

式(3)中：狀態量()=[▽▽▽],其中、、為平臺角誤差，、、代表速度誤差，、、為位置誤差；()=[]，其中、、為陀螺儀的隨機噪聲，、、為加速度計的隨機噪聲；()為系統矩陣；()為噪聲驅動矩陣。

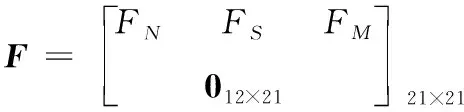
(4)

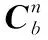
2.4 量測模型

自標定系統以差分GPS與慣導解算后的導航信息之差作為觀測量，系統的觀測值可以是單一量測，也可以是量測組合。本文采用位置/速度差分GPS方式，在慣導解算時，純慣導高度通道易發散，所以本文采用水平方向速度和位置誤差參數作為觀測量。有以下3種不同的形式。

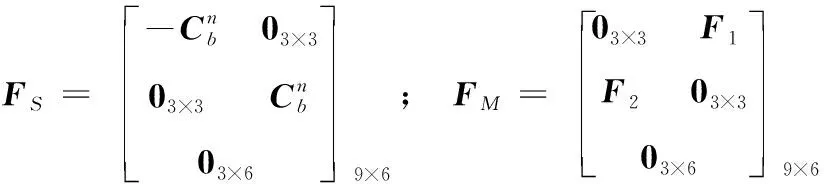
速度匹配以機場附近差分GPS與慣導解算的速度差值作為量測量，量測模型為：

()=()+()

(5)

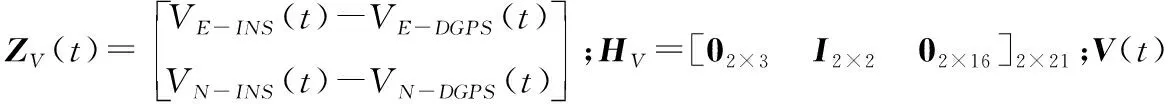
位置匹配以機場附近差分GPS與慣導解算的位置差值作為量測量，量測模型為：

()=()+()

(6)

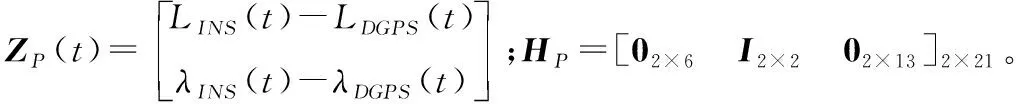
“速度+位置”匹配以機場附近差分GPS與慣導解算的速度和位置差值作為量測量，量測模型為：

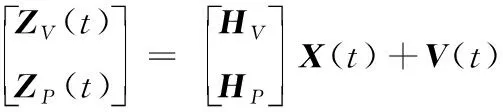
(7)

3 慣導起飛階段自標定可觀測性分析

3.1 基于PWCS的可觀測性分析

若直接進行可觀測矩陣求解，根據能觀測性的判斷條件，能夠計算出Grammian矩陣為：

(8)

式(8)中，(,)是系統從到的狀態轉移矩陣。

該方法計算量過大并且結果無法理論分析。為了簡化計算，Goshen-Meskin等提出了分段線性定常系統方法，該方法的主要思路是：將系統的運行時間按照適當的間隔進行分段處理，由于、在每個時間段內變化較為緩慢，因此將其近似為常量處理，則在該時間段內，該系統可以當作線性定常系統，那么，系統在整個運行時間內，能夠被看作分段線性定常系統。這種近似處理對于系統精度和特性影響較小，并且能夠較大程度上降低計算量，簡化分析流程，因此PWCS能夠用于空中標定系統的可觀測性分析。

對系統整個時間段進行分段線性定常處理后，可求出系統在第個時間段內的可觀測性矩陣為：

(9)

式(9)中：是系統第個時段中狀態矩陣常值：即為系統觀測矩陣。

將系統從第1個時間段到第個時間段的可觀測性矩陣組合到一起，即得到總可觀測矩陣(TOM)為：

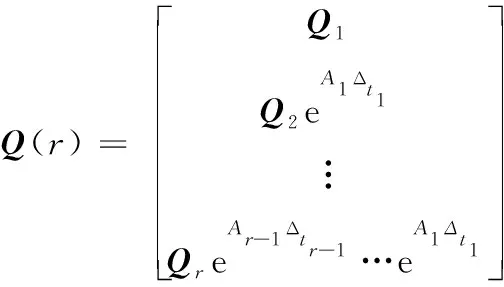
(10)

式(10)中，Δ是第個時間段的時間長度。

式(10)中存在指數函數矩陣項，使得計算量變得較為復雜，引入()作為系統的提取可觀測矩陣(SOM)，有：

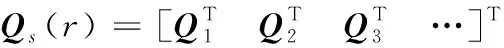
(11)

若null()?null()，1≤≤，則

(12)

式(12)中：null(·)代表矩陣的零空間；rank(·)代表矩陣的秩。

若系統滿足上述條件，則可以利用SOM代替TOM，實現可觀測性分析，此時系統的觀測方程為：

=()

(13)

當()的秩與系統階數相等時，整個系統的狀態變量都可以被估計出來，即系統是完全可觀測的；反之，當()的秩比系統階數小時，系統只有部分狀態量或狀態量組合能夠被估計出來，即系統不完全可觀測。

3.2 基于SVD的可觀測度分析

由31節分析可知，()的秩可以確定一個系統是否完全可觀測或部分可觀測，但是對部分可觀測系統，確定不了哪些狀態可觀測哪些狀態不可觀測。根據文獻[18]提出的基于SVD的可觀測度方法，將式中的()奇異值分解，得：

=

(14)

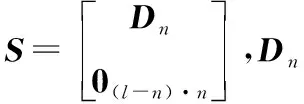
經過奇異值分解后，式(13)可轉換為：

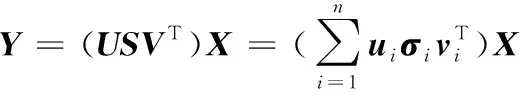
(15)

化簡得：

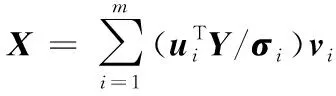
(16)

易知，當=min(,)時，(0)存在唯一解，此時系統完全可觀測；反之，當(0)存在無數解，此時系統不能實現全部狀態的估計。

在定量分析各狀態量時，根據式(16)，能夠計算與奇異值相對應的狀態分量，隨后進行數值對比，奇異值較大時，該狀態量能夠得到較好的估計；反之，奇異值較小時，該狀態量估計效果差或者不可觀測。進一步分析，可以定義系統某個狀態的奇異值與外部觀測的狀態相對應的奇異值的比值為系統該狀態的可觀測度。

(17)

根據系統各時間段內狀態的可觀測度，對比分析空中自標定系統的狀態估計效果。

4 慣導自標定可觀測性計算分析

4.1 機動階段和仿真參數設置

飛機的主要機動過程有靜止、加速、起飛、爬升、改平、平飛、轉彎、滾轉等。主要分為6個階段：

1) 靜止階段：飛機停在機場，此時系統為時不變系統。

2) 加速階段：加速度設置為6.5 m/s，將飛機速度從0 m/s提升至90 m/s。

3) 起飛階段：設飛機以90 m/s速度起飛，首先進行變角度爬升，將飛機以2(°)/s的俯仰角拉升到30°；隨后保持角度爬升一段時間；最后將飛機改平，起飛階段完成。起飛和降落過程完全相反，可觀測性基本一致，無需再單獨分析。

4) 平飛階段：飛機在機場附近保持100 m/s的速度勻速飛行。

5) 滾轉階段：飛機在機場附近以165 m/s速度飛行，首先將飛機以5(°)/s左滾轉至45°，隨后勻速飛行一段時間，最后將飛機以5(°)/s右滾轉到水平。

6) 轉彎階段：飛機在機場附近以165 m/s速度飛行，首先將飛機以9(°)/s右轉彎至90°，隨后勻速飛行一段時間，最后將飛機以9(°)/s左轉彎至原來的方向繼續前進。

4.2 計算結果與分析

本文采用上述飛行機動階段和仿真參數，基于速度誤差為觀測量，對不同機動條件下狀態變量的可觀測度進行分析。基于速度匹配的起飛階段自標定模型可觀測度如表1所示。

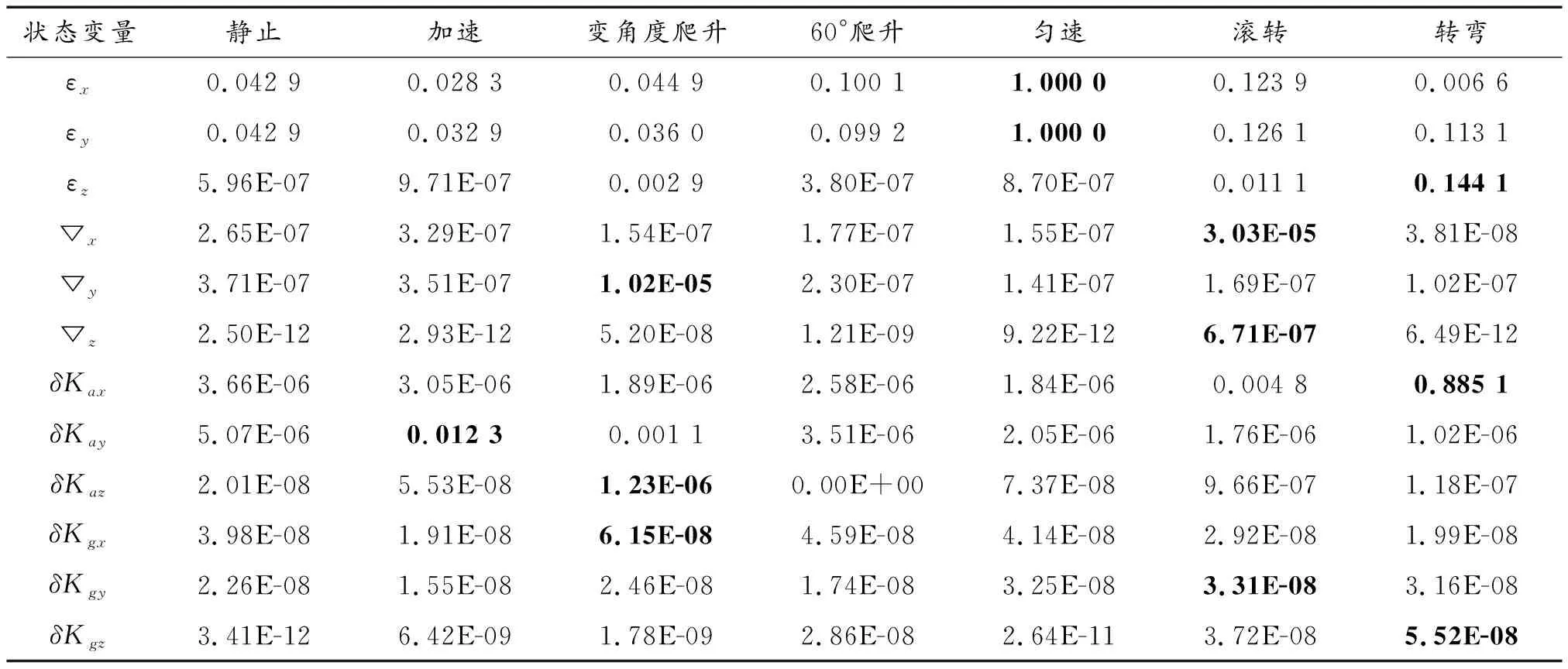
表1 不同機動條件下各狀態變量的可觀測度結果Table 1 Observability results of state variables under different maneuvering conditions

根據表1中的奇異值，得如下結果：

1) 靜止狀態下各狀態的可觀測度都較差。

2) 整個系統本身的可觀測度較差，但是可以通過不同的機動方式，實現對不同狀態變量的激勵，從而達到慣導誤差標定的目的。

3)、在勻速階段的可觀測性提升顯著，狀態變量完全可觀測；在爬升階段的可觀測度有所提高，在滾轉和轉彎階段能夠得到進一步的提高。

4) 后9個狀態變量本身數值較小，使得對應的奇異值數值同樣小，但是不同的機動條件，其奇異值也有較大差別。可以從中得出機動動作對狀態變量的激勵效果。

5) ▽、▽可觀測性較弱，在滾轉和變角度爬升階段激勵效果進一步提高。▽在變角度爬升階段和滾轉階段有一定的激勵效果。在轉彎階段能夠得到一定的激勵效果，在加速階段能夠被激勵出來，在爬升階段激勵效果有所提高。

6)、、的可觀測度均在E-8以下，整體可觀測度較差，但是在不同的動作激勵下會有一定的改善。其中在爬升階段激勵效果有所提高，在滾轉階段有一定的激勵效果，在轉彎階段有一定的改善。

5 慣導起飛階段自標定仿真分析

5.1 飛行軌跡設計

通過飛行軌跡的設計，能夠使得系統更好地激勵出系統狀態參數，從而使慣性器件的誤差項能被更好地標定出來。

在飛行過程中，GPS存在精度要求無法長時間保證的問題，則充分利用起飛階段飛機的機動以及機場跑道附件能夠布設高精度GPS差分站的優勢，將空中自標定的軌跡設置在機場附近。根據上述不同機動條件下的可觀測性分析結果，設計恰當的飛行軌跡，且保證充分利用機場附近高精度的差分GPS。根據某型飛機的起飛機動特性以及機場的數據，在盡可能不增加飛行員額外操作的原則下設計起飛標定動作，如表2所示，共21個階段，將起飛階段和盤旋階段相結合，共590 s。

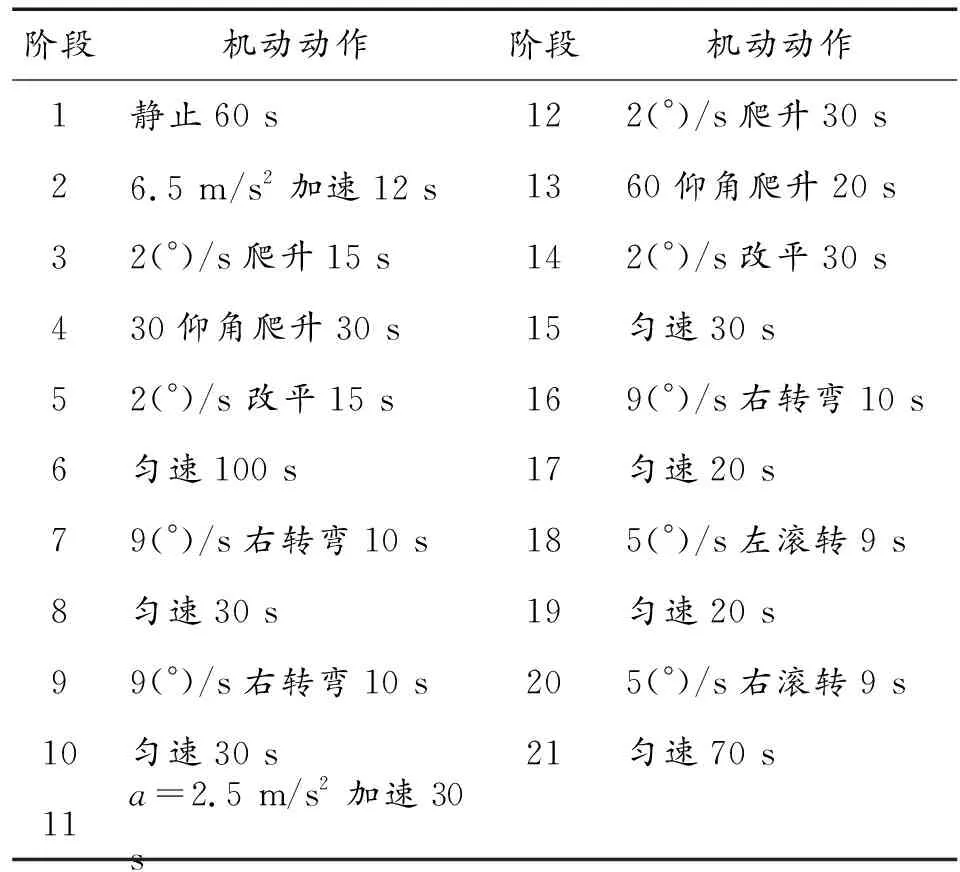
表2 飛機機動動作要求Table 2 Aircraft maneuver requirements

飛行軌跡圖如圖1所示，所設計飛行軌跡需要覆蓋機場上空8 000 m高度，水平方向15 km，機場差分GPS適用于100 km以內區域，能夠覆蓋本文設計飛行區域。

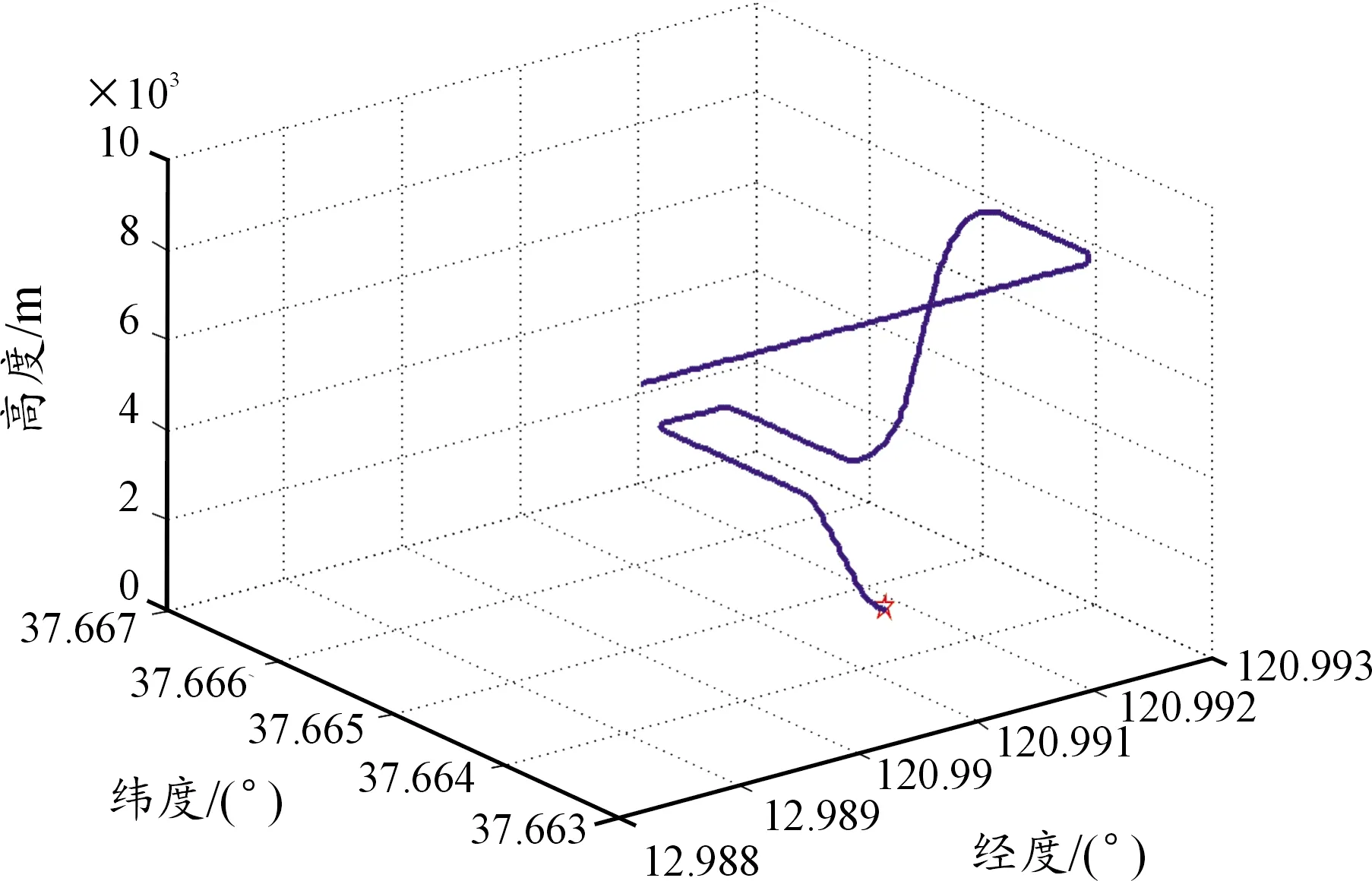
圖1 飛行軌跡圖Fig.1 flight path diagram

5.2 仿真結果分析

慣導起飛階段自標定采用Kalman濾波器，仿真與可觀測性分析仿真條件相同，其中慣性導航解算周期設置為0.04 s,濾波周期設為 1 s,系統各狀態的初值設置為零，Kalman濾波初值設定如下。

初始誤差協方差陣為：

(0)=diag([20″；20″；30′；0.2 m/s；0.2 m/s；0.2 m/s；

1 m；1 m；1 m；0.01(°)/h；0.01(°)/h；0.01(°)/h；

50 μg；50 μg；50 μg；100×10；100×10；

100×10；100×10；100×10；

100×10]×10)

系統噪聲方差陣為：

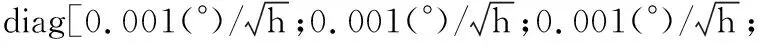
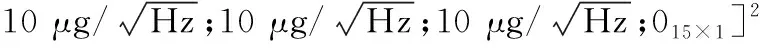
觀測量的匹配方式決定了系統的量測誤差方差陣,有以下3種方式：

1) 以速度誤差為觀測量，有：

=diag[0.2 m/s；0.2 m/s]

2) 以位置誤差為觀測量，有：

=diag[1 m；1 m]

3) 以“速度+位置”誤差為觀測量，有：

=diag[0.2 m/s；0.2 m/s；1 m；1 m]

根據4.1節的仿真參數和5.1節設計的飛行軌跡，結合濾波初值條件，進行仿真，分別以速度、位置、速度+位置誤差為觀測量，利用Kalman濾波實現慣性器件誤差項分離和估計，仿真結果如圖2、圖3所示，其中，紅色虛線、青色實線和紫色點畫線分別代表以“速度+位置”誤差、速度誤差和位置誤差為觀測量時慣性器件的誤差估計曲線。

圖2 機動條件下的陀螺儀漂移與加速度計零偏誤差估計曲線Fig.2 Gyro drift and accelerometer bias error estimation curve under maneuver condition

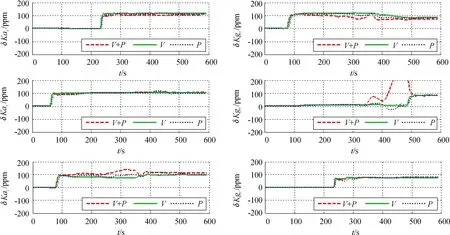
圖3 機動條件下的陀螺儀與加速度計標度因數估計曲線Fig.3 Scale factor estimation curve of gyroscope and accelerometer under maneuver condition

1) 從圖2、圖3中可以看出，以“速度+位置”誤差為觀測量時,、估計值較差；以位置誤差為觀測量時，陀螺儀3個方向估計值均較差；相比之下，以速度誤差為觀測量，除估計效果較差外，慣性器件其他各項誤差均能被較好地標定出來。

2) 根據圖2、圖3結果分析，在參數相同情況下，以速度誤差為觀測量，標定結果精度較高。

3) 此處以對速度誤差為觀測量進行分析，根據圖2、圖3的標定結果，結合表2的飛行機動和表1的可觀測度分析數據可得，靜止時，僅▽、▽有一定的激勵效果，但不能完全激勵出誤差值；大多數誤差項需要機動條件去激勵出來。在加速階段,能夠被較好地激勵出來；在飛機變角度爬升階段, ▽、▽、、能夠被激勵出來；在飛機60°傾角爬升階段,有一定的激勵效果；在飛機改平階段，、▽的激勵效果有進一步的提高；在飛機改平后的勻速飛行階段，、均能被激勵出來；在滾轉階段，能被激勵出；在飛機左右轉彎階段，、可以被激勵出來。可觀測度分析結果與仿真激勵效果相一致。

4) 陀螺儀軸的常值漂移未能較好地激勵出來，原因為天向陀螺漂移可觀測性較差。結合可觀測性分析結論，在飛行軌跡設計階段，可以考慮增加存在角運動的機動動作和時間，從而使上述誤差量能更好地被激勵出來，進而實現機載SINS全參數自標定。

為進一步驗證所提方法的有效性，以速度誤差為觀測量，將常規起飛過程和本文所設計的機動過程仿真結果進行對比分析，常規起飛過程即飛機從地面靜止到空中勻速飛行過程，通常情況下為表2機動動作中的前6個階段，標定結果如表3所示。

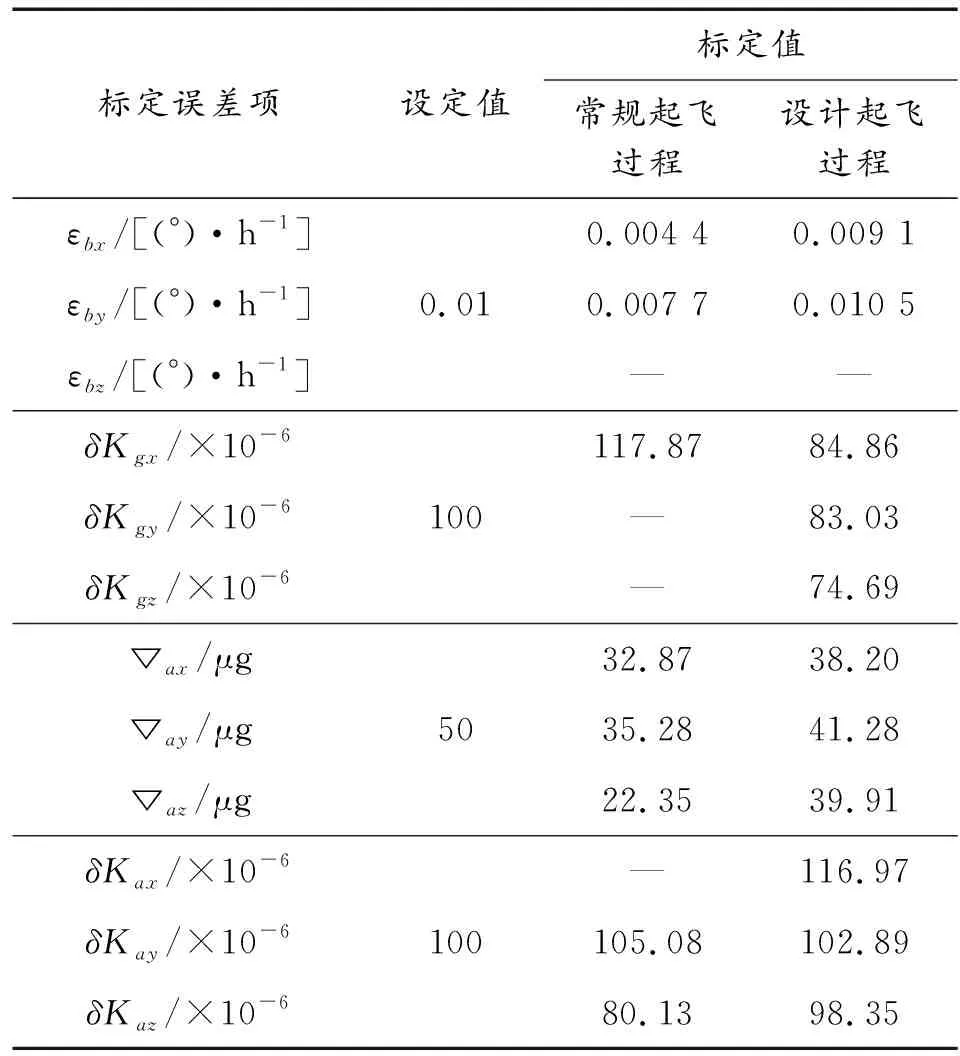
表3 慣導器件誤差標定結果Table 3 Comparison of calibration results of inertial navigation deviceerror

根據表3知，所設計的機動，相較于常規起飛過程，慣導誤差標定精度均有所提高，且部分參數在添加一系列機動后，成功地被激勵出來，進一步證明了本文所提方法的有效性。

根據上述分析知：可觀測度高低能夠直接反映觀測模型對標定參數的估計能力，據此提出機載SINS起飛階段的自標定方法，對比3種觀測量起飛階段自標定，以速度誤差為觀測量能夠實現較好的標定效果，同時，將常規起飛過程和本文所設計的起飛過程的慣導系統自標定進行仿真對比分析，驗證了本文標定方法的有效性。根據機動條件的可觀測性，不同的機動條件可以提高狀態變量的激勵效果，也可以通過適當提高機動時間，提高狀態變量的激勵效果。

6 結論

機載SINS空中自標定能夠滿足慣導免拆卸的需求，能夠提高飛機的日常維護效率。提出一種基于可觀測性分析的機載SINS起飛階段自標定方法，建立了慣導標定模型，采用基于PWCS的奇異值分解方法，對機動方式不同時，系統狀態變量可觀測度進行分析比較，不同的機動條件可以提高狀態變量的激勵效果，設計了一種充分利用機場附近差分GPS和機動條件的飛行軌跡。對3種基于不同觀測量的慣導起飛階段自標定分別進行仿真分析，基于速度誤差觀測量的慣導起飛階段自標定方法精度較高，驗證了本文標定方法和可觀測性分析結論的有效性，具有實際意義。