典型含鋁炸藥深水爆炸氣泡脈動特性研究

段超偉，宋 浦

(西安近代化學研究所, 西安 710065)

1 引言

現今世界，各國現役潛艇在作戰時的下潛深度一般在300～400 m，極限下潛深度甚至能夠達到數千米。隨著水深的增加，靜水壓力隨之升高，水下環境也變得更為復雜，魚雷、水雷等水下兵器在深水高壓環境下起爆后的爆炸氣泡運動特性也會有所變化，深水中氣泡脈動載荷的變化對潛艇的毀傷作用的影響是不可忽視的，因此，開展炸藥深水爆炸氣泡運動特性研究對深水潛艇、反潛艇作戰和深水兵器的研發具有非常重要的意義。

早期國內外研究人員在炸藥深水爆炸氣泡運動特性方面開展了一定的研究。Slifko通過大量的海上實驗對深水爆炸載荷的特性進行了細致的研究，并給出了多種炸藥深水爆炸沖擊波峰值壓力、氣泡脈動峰值壓力與水深、比距離等參數的關系。Cole在其著作《Underwater explosion》中給出了260 m深度內的氣泡脈動周期與水深關系的實驗結果。馬坤等通過增加水面大氣壓強模擬靜水壓力建立了可模擬深水環境的爆炸容器，并獲得了小當量(1～1.25 g)球形裝藥深水(10～110 m)爆炸試驗的氣泡脈動過程，分析了氣泡脈動周期與最大半徑與模擬水深的關系。魯忠寶等采用LS-DYNA建立了典型裝藥在不同深水處爆炸的有限元模型，進行了不同水深壓力下爆炸氣泡運動規律的仿真研究。梁浩哲等對深水條件下50 g TNT球形藥包的爆炸進行了數值模擬計算，得到了水下爆炸的沖擊波峰值壓力衰減過程及氣泡脈動過程。針對深水爆炸的實驗及數值模擬研究多是以TNT等理想炸藥為研究對象，且裝藥量一般較小，極少涉及含鋁炸藥深水爆炸氣泡運動特性的研究。

本文采用數值計算方法，分別對100 g和10 kg兩種裝藥量下的RS211含鋁炸藥深水爆炸氣泡脈動參數進行計算，獲得了水深范圍在100～2 000 m內的含鋁炸藥水下爆炸氣泡脈動過程，通過對比不同深度的海水環境下，氣泡脈動最大半徑、脈動周期、脈動峰值壓力和氣泡能的變化過程，分析深水中靜水壓力對水下爆炸氣泡脈動特性的影響。

2 深水爆炸氣泡脈動數值計算

2.1 氣泡脈動半徑及周期

根據水下爆炸流場變化特性，對氣泡脈動過程和流場特性進行合理簡化，并且考慮流體黏性、蒸汽壓力和張力的影響，得到不可壓縮流體球形氣泡的運動方程：

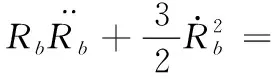
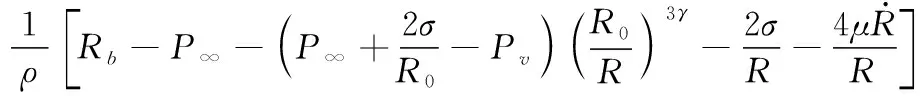
(1)

式中：為氣泡脈動半徑；=1 000 kg/m為水的密度；為炸藥所處水深處的靜水壓力；為氣泡內壓；=2 338 Pa為水蒸汽壓力；=14為氣體多方指數；為液體表面張力；為流體黏性系數。

隨水深的增加，海水溫度逐漸降低，2 000 m深處的海水溫度約2 ℃，海水張力系數和粘性系數均會隨溫度的降低而升高，張力系數在3～30 ℃的變化率在6%左右；粘性系數在5～25 ℃的變化范圍為0.95×10～1.57×10m/s。因此，深水中爆炸需要考慮靜水壓力、流體張力與流體黏性等多方面環境因素的影響，將不同水深對應的流體張力與黏性系數代入氣泡脈動方程的計算中，并通過=+換算炸藥水深處的流體靜壓。

氣泡內壓可由爆轟產物的狀態方程確定，考慮含鋁炸藥的爆轟特性，選取JWL狀態方程來描述RS211炸藥的爆轟過程：

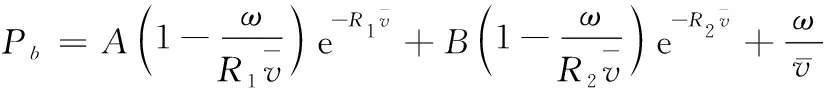
(2)

JWL狀態方程既可用來描述爆炸沖擊載荷的高壓段，也可描述低壓段，能夠比較準確地描述含鋁炸藥爆轟產物的膨脹驅動過程。

RS211炸藥的JWL狀態方程參數如表1所示。

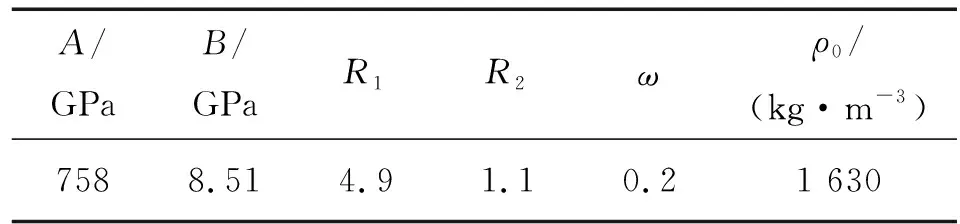
表1 RS211炸藥的JWL狀態方程參數Table 1 JWL state equation parameters of RS211 explosive

聯立式(1)、式(2)求解可以得到氣泡脈動半徑時程曲線，選取氣泡脈動初始時刻到第一次脈動到最小半徑時刻為一個脈動周期，既可得到深水爆炸氣泡脈動最大半徑與脈動周期值。

2.2 氣泡脈動壓力

水下爆炸氣泡的脈動過程會在水中產生較高的脈動壓力，利用合不可壓縮理想流體一維流動的運動方程，可以得出水中氣泡脈動壓力的變化過程為

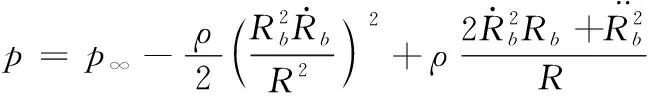
(3)

式中：為距裝藥中心的距離；為裝藥所處水深的靜水壓力。

2.3 氣泡能

Bjarnholt通過大量實驗及理論分析建立了系統的水下爆炸能量輸出特性及其評價方法，獲得了不同炸藥水下爆炸的能量輸出參數，其中定義了氣泡能為氣泡膨脹到半徑最大值時刻對周圍水介質所做的功，具體為：

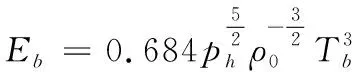
(4)

式中：為水深處的靜水壓力；為水的密度；為氣泡脈動周期。利用式(4)便可計算不同水深下，水下爆炸的氣泡能。

3 氣泡脈動計算模型驗證

聯立式(1)和式(2)可以計算RS211炸藥水中起爆后的氣泡脈動周期，將計算結果與RS211炸藥水下爆炸實驗測量的氣泡脈動周期結果列表分析，如表2。

表2 RS211炸藥水下爆炸氣泡脈動周期計算和實驗結果Table 2 Comparison of calculated value and experimental value of bubble pulsation period of RS211 explosive

由表2可知，RS211炸藥水下爆炸氣泡脈動周期計算結果與實測結果對比的誤差均在3%以內，具有良好的計算精度，因此，該模型可應用于RS211含鋁炸藥水下爆炸氣泡脈動周期的計算。

4 數值計算結果及分析

4.1 數值計算工況

計算時分別選取100 g、10 kg兩種藥量的RS211球形炸藥進行深水爆炸實驗計算，并設置12種計算水深工況，分別為100 m、200 m、300 m、400 m、500 m、600 m、800 m、1 000 m、1 200 m、1 500 m、1 800 m、2 000 m。在計算時根據不同水深選取對應的流體特性參數。

4.2 深水爆炸氣泡脈動最大半徑

圖1為2種裝藥量的不同深度工況下，氣泡脈動最大半徑的變化曲線。從圖1中可以看出，氣泡脈動最大半徑隨著水深的增加而減少，并且100 g和10 kg藥包的變化趨勢一致：在水深小于500 m的范圍內，氣泡脈動最大半徑受水深變化的影響尤為明顯；而當水深超過1 000 m時，氣泡脈動最大半徑隨水深增大的變化趨勢放緩。隨著水深的增加，入水深度對水下爆炸氣泡脈動最大半徑的影響逐漸變小。

圖1 氣泡脈動最大半徑隨深度的變化曲線Fig.1 Curve of the maximum radius of bubble pulsation with depth

Cole針對TNT炸藥水下爆炸提出的氣泡脈動最大半徑的經驗公式為：

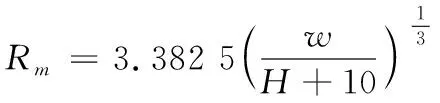
(5)

其中：為裝藥質量，為裝藥所處水深。

由式(5)可知，在深度不變的情況下，氣泡脈動最大半徑與炸藥質量的立方根呈線性關系。為了有效利用計算數據，獲得深水爆炸氣泡脈動最大半徑隨深水增加的衰減關系，將氣泡脈動最大半徑與炸藥當量立方根之比和計算水深之間的關系用曲線擬合，結果如圖2所示。

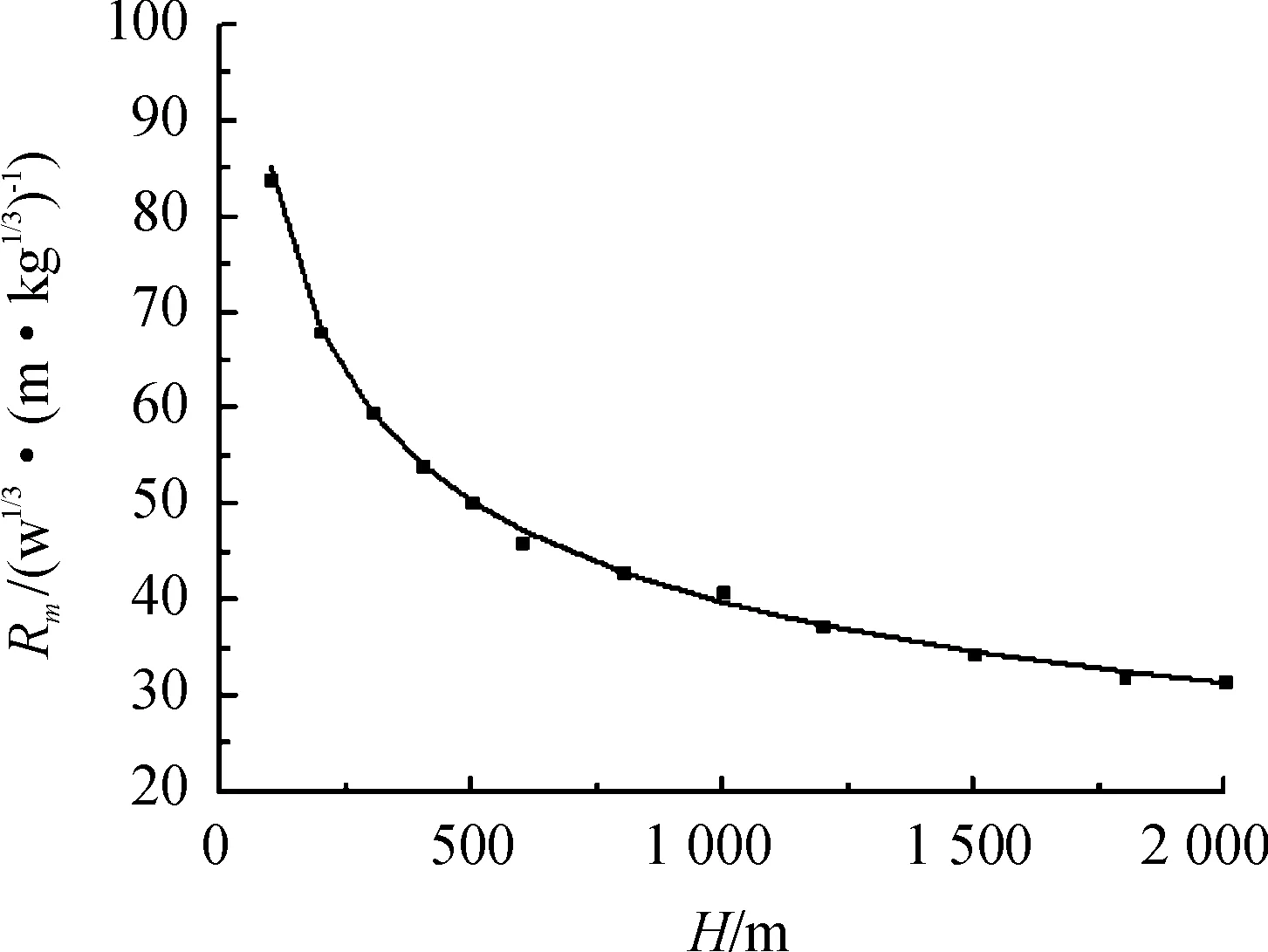
圖2 氣泡脈動最大半徑與炸藥當量立方根之比隨深度的變化曲線Fig.2 The variation curve of the ratio of the maximum radius of the bubble pulse to the cube root of the explosive equivalent with the depth

圖2中大部分數據點偏離擬合曲線較小，擬合曲線的炸藥系數為4.285，氣泡脈動最大半徑隨水深的衰減系數為0.344，與經驗公式(5)的系數1/3吻合較好，說明通過該數值計算模型可以得到氣泡脈動最大半徑隨水深的衰減規律，計算結果擬合得到的氣泡脈動最大半徑的函數表達式為：

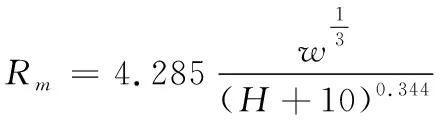
(6)

式中：為氣泡脈動最大半徑(m);為藥量(kg);為水深(m)。

擬合曲線的函數表達式與經驗公式相比，氣泡脈動最大半徑隨水深的衰減系數一致，最大的區別在于炸藥系數，Cole的經驗公式僅適用于TNT炸藥，不適用于RS211含鋁炸藥，因此根據本文計算結果擬合出的炸藥系數為4.285。

4.3 深水爆炸氣泡脈動周期

不同深度水下爆炸氣泡脈動周期變化如圖3所示。氣泡脈動周期和最大氣泡半徑一樣，隨著藥包入水深度的增加而減少，且同樣以500 m深度為分界線，深度小于500 m時，氣泡周期隨水深增加的減小趨勢明顯，深度大于1 000 m時，小當量裝藥量下的氣泡脈動周期隨水深的增加的變化幾乎可以忽略。隨著水深的增加，入水深度對水下爆炸氣泡脈動周期的影響也會逐漸變小。

圖3 氣泡脈動周期隨深度的變化曲線Fig.3 Curve of bubble pulsation period with depth

Cole針對TNT炸藥水下爆炸提出的氣泡脈動周期的經驗公式為：

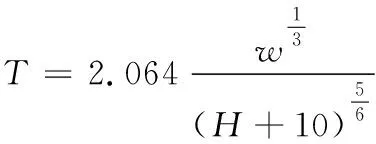
(7)

其中：為裝藥質量，為裝藥所處水深。

由式(7)可知，在深度保持不變的情況下，氣泡脈動周期與炸藥質量的立方根呈線性關系。為了獲得深水爆炸氣泡脈動周期隨深水增加的衰減關系，將氣泡脈動周期與炸藥當量立方根之比和計算水深之間的關系用曲線擬合，結果如圖4所示。

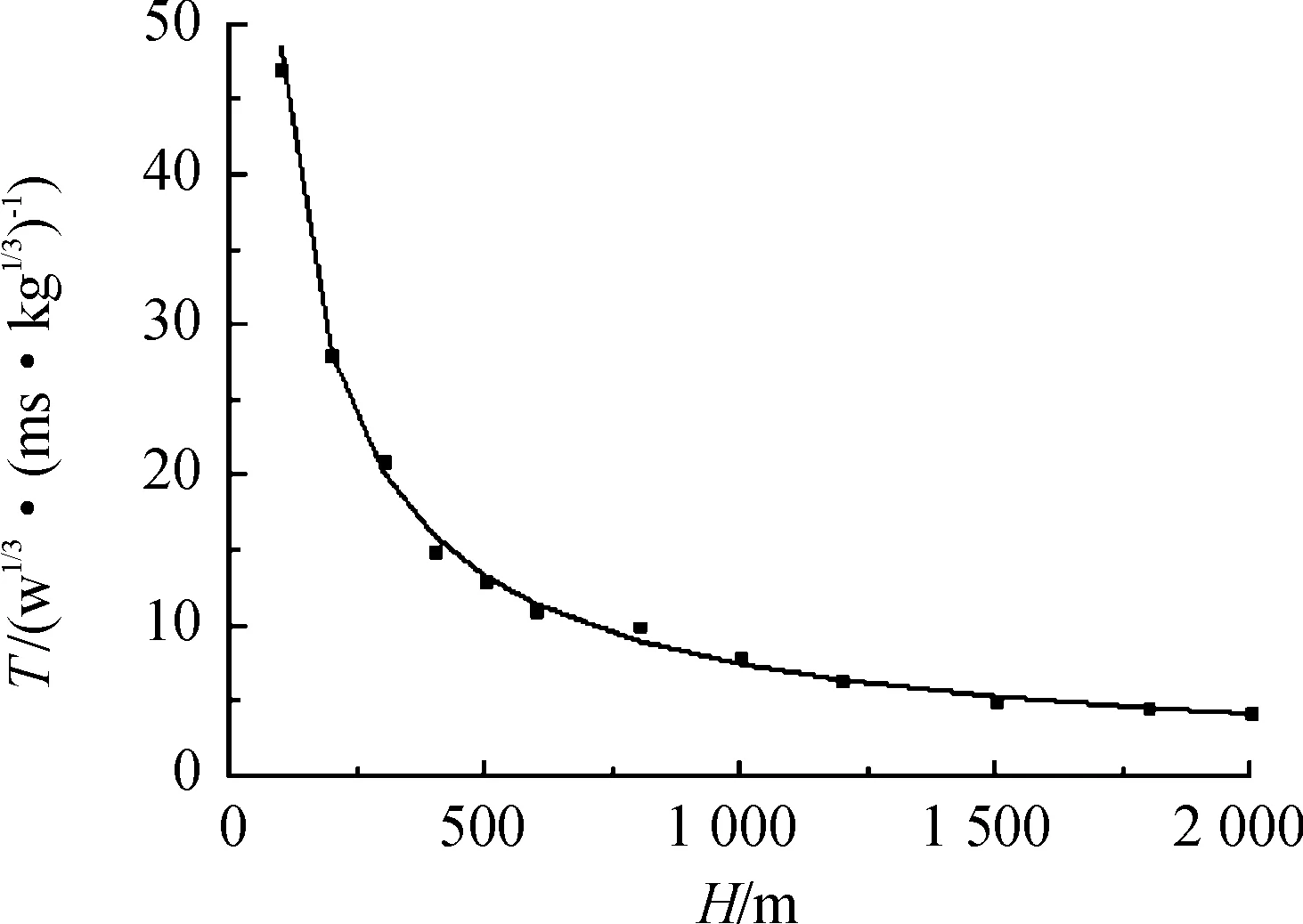
圖4 氣泡脈動周期與炸藥當量立方根之比隨深度的變化關系曲線Fig.4 The variation curve of the ratio of the bubble pulse period to the cube root of explosive equivalent with depth

圖4中大部分數據點在擬合曲線附近，擬合曲線的炸藥系數為2.545，氣泡脈動周期隨水深的衰減系數為0.842，與式(7)的系數5/6吻合較好，說明通過該數值計算模型可以得到氣泡脈動周期隨水深的衰減規律，計算結果擬合得到的氣泡脈動周期的函數表達式為：

(8)

式中：為氣泡脈動周期(s);為藥量(kg);為水深(m)。

擬合曲線的函數表達式與經驗公式中的氣泡脈動周期隨水深的衰減系數一致，因為本文選取的炸藥種類不同，含鋁炸藥RS211水下爆炸氣泡脈動周期計算結果擬合出的炸藥系數為2.545，與經驗公式存在差異。

4.4 深水爆炸氣泡脈動峰值壓力

利用式(3)計算距離裝藥中心為的氣泡脈動壓力，圖5為100 g藥包深水爆炸下，距裝藥中心0.5 m、1 m、1.5 m處氣泡脈動峰值壓力的變化曲線。圖6為10 kg藥包深水爆炸下，距裝藥中心2 m、2.5 m、3 m處氣泡脈動峰值壓力的變化曲線。

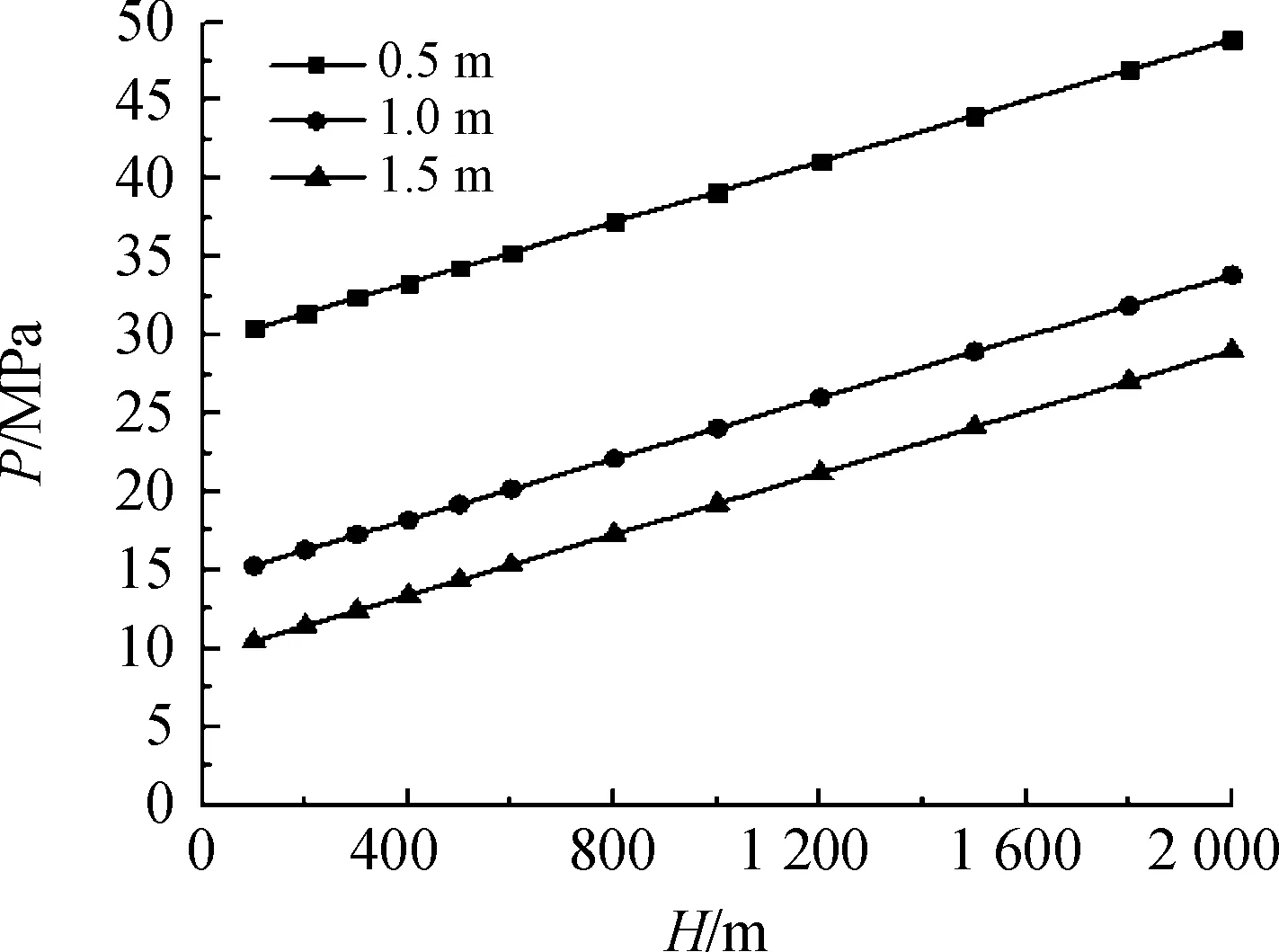
圖5 100 g炸藥深水爆炸氣泡脈動峰值壓力曲線Fig.5 Peak pressure of bubble pulsation of 100 g explosive

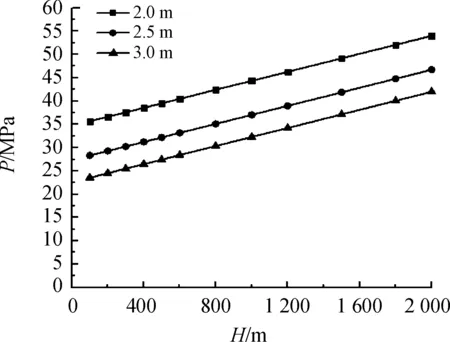
圖6 10 kg炸藥深水爆炸氣泡脈動峰值壓力曲線Fig.6 Peak pressure of bubble pulsation of 10 kg explosive

從圖5、圖6中可以看出，2種裝藥量下的RS211藥包深水中爆炸，各點的氣泡脈動的峰值壓力均與水深成線性關系，且在同一點的脈動峰值壓力的增加量是隨水深增加的靜水壓力的增加量，這說明含鋁炸藥在深水中爆炸的氣泡脈動峰值壓力基本不會受到深水高壓環境的影響，同一水深處，脈動峰值壓力只與裝藥量和壓力點距裝藥中心的距離有關。

4.5 深水爆炸氣泡能

利用式(4)可以計算得到炸藥深水爆炸的氣泡能，計算結果如表3所示，從表中可以看出，在相同水深下，氣泡能與裝藥量成正比關系，大當量藥包的裝藥量與氣泡能均為小當量藥包的100倍，這可能與選取的氣泡脈動計算模型有關，在計算時，將藥包假設為完全爆轟，而炸藥在深水高壓力環境下是否可以完全爆轟，則需要進一步的實驗研究。

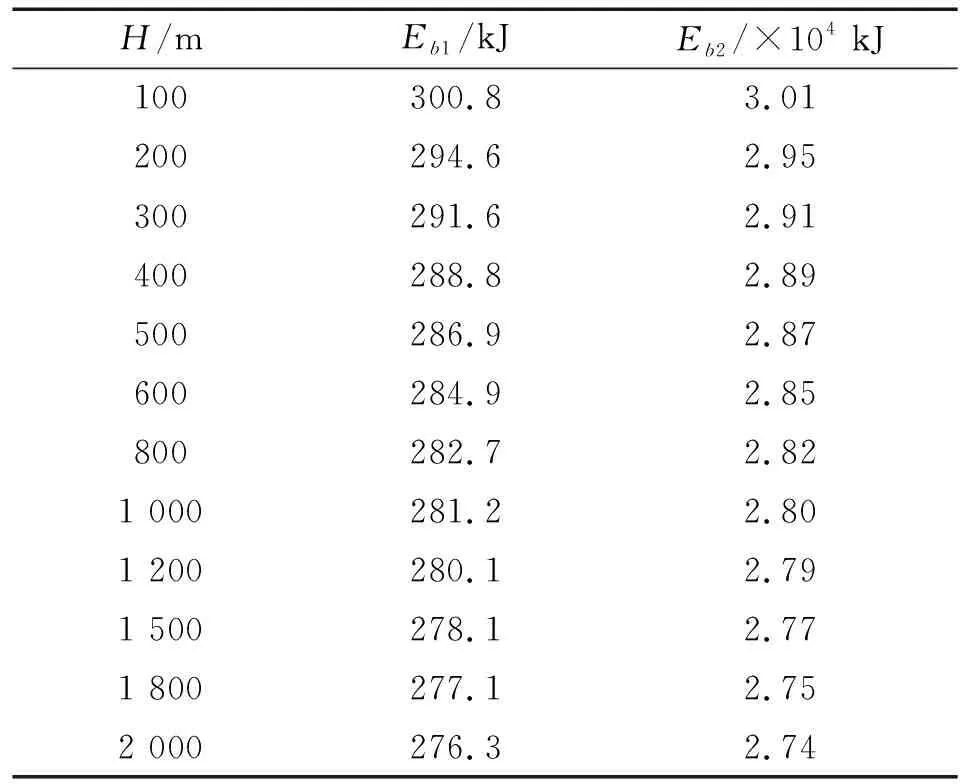
表3 RS211炸藥深水爆炸氣泡能計算結果Table 3 The bubble energy of RS211 explosive deep water explosion

100 g RS211炸藥深水爆炸氣泡能和10 kg RS211炸藥深水爆炸氣泡能隨水深的變化曲線如圖7、圖8所示，從圖中可以看出，2種裝藥量下的氣泡能變化趨勢一致，隨著入水深度的增加，炸藥水下爆炸釋放的氣泡能逐漸減小，在100～600 m的變化較大，而在600 m之下的氣泡能變化趨于緩和，幾乎呈線性減小，反映出與氣泡脈動行為一致的變化特性，說明靜水壓力的變化會影響到炸藥水下爆炸能量的輸出特性。造成上述結果的原因可能是：炸藥入水深度的增加，環境壓力也增大，水的密度增大，水的黏性也隨之增大，爆炸氣泡在脈動過程中會損耗更多的能量，因此氣泡脈動能量隨著水深的增加而減小。

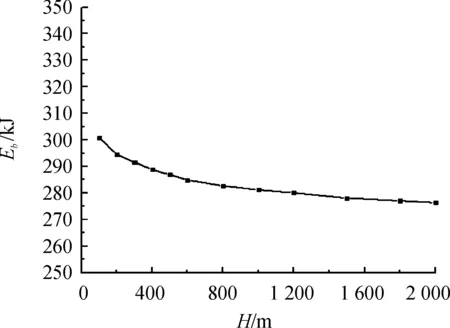
圖7 100 g RS211炸藥深水爆炸氣泡能變化曲線Fig.7 Curve of bubble energy of 100 g RS211 explosive

圖8 10 kg RS211炸藥深水爆炸氣泡能變化曲線Fig.8 Curve of bubble energy of 10 kg RS211 explosive

5 結論

1) 氣泡最大半徑與脈動周期均隨著炸藥入水深度的增加而減小。

2) 氣泡脈動的峰值壓力與水深成線性關系，氣泡脈動峰值壓力基本不受深水高壓環境的影響；同一水深處，脈動峰值壓力的大小只與裝藥量和壓力點距裝藥中心的距離有關。

3) 隨著入水深度的增加，炸藥水下爆炸釋放的氣泡能逐漸減小，在100～600 m的變化較大，而在600 m之下的氣泡能變化趨于緩和，呈線性減小，與氣泡脈動行為一致，說明靜水壓力的變化會影響到炸藥水下爆炸能量的輸出特性。

4) 100 g裝藥量和10 kg裝藥量的含鋁炸藥深水爆炸氣泡脈動參數隨水深的變化趨勢一致。在深水爆炸中，裝藥量不會影響氣泡的脈動特性。但炸藥在深水高壓力環境下是否可以完全爆轟，需要進一步的實驗研究。