基于“高觀點”視角，促進學生主動建構知識

顧新佳

【摘 要】新課程改革背景下，數學知識的學習不斷追求“深入淺出”，呼喚對數學本質的關注，期待知識結構體系的建構，重視數學思維能力的提升。本文結合特級教師周衛東“平行四邊形的面積”一課，分析如何站在一個較高的視角統領學習任務，在教學中力求順應學情、深究本質、建立體系、發散思維，促進學生主動建構知識。

【關鍵詞】高觀點 數學知識 主動建構

近日，筆者觀摩周衛東老師執教的“平行四邊形的面積”一課，對周衛東老師一貫堅守的“高觀點”教學主張有了更深的認識。本節課順應學情、深究本質、站位高遠，幫助學生突破知識本質，促進學生主動建構知識。

一、大問題統整，促進學生主動建構知識

“德國著名數學家、數學教育家克萊因倡導‘高觀點’，即從高等數學的角度來審視初等數學。“高觀點”給初等數學的教學帶來了生機與活力。”受上述觀點的啟發，周衛東老師積極倡導基于“高觀點”視角的數學教學。他認為：“所謂‘高’者，即不一般、優于常態也，‘高觀點’視角下的數學教學，可以從內容的縱深維度遷移到內容的寬窄維度，推及思想的高低維度等。”“高觀點”視角下的數學教學，立于教學的高位，回應數學學科的本質。

教學中，通過大問題統整，可以幫助學生主動建構知識。所謂大問題，就是一種開放性問題或具有多元思考方式的問題，來鼓勵學習者積極參與問題解決中，使學生嘗試尋找有用的知識、思考合適的方案來解決主要問題。數學學習中的大問題觸及數學本質，是課堂教學中的問題之“眼”。

（一）大問題引領，促數學思維萌芽

周衛東老師在執教“平行四邊形的面積”一課時，緊緊扣住“平行四邊形的面積到底該怎么計算”這個大問題統領教學。

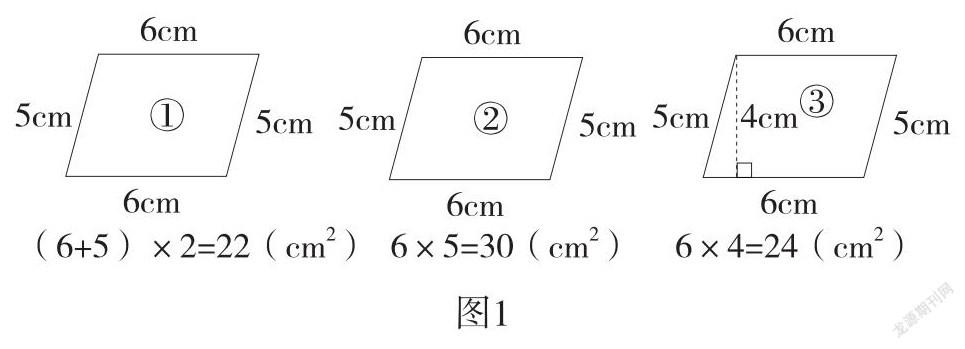
上課伊始，周衛東老師出示學生課前小研究的三種典型算法：

課堂上，當三種算法呈現出來時，學生紛紛舉手，準備表達觀點。這時，周衛東老師提醒學生說：“如果你想要證明哪一種結果是對的，就要說出你的方法。”看似平常的提醒，卻為學生后面沿著大問題的脈絡一步一步接近數學知識的本質奠定了基礎。

學生經過交流，很快得出了結論。方法①是算周長的，不符合條件。而方法②，是課前預習中學生常出現的錯誤之一，為什么這種方法不對呢？學生從長方形的面積計算中得到啟發，認為平行四邊形不是長方形，所以不能用鄰邊相乘來計算。對于方法③，絕大多數學生認為是對的，這多源于課前預習。基于這樣的學習起點，周衛東老師在“平行四邊形的面積到底該怎么算”這個大問題的統領下，拋出了“怎么說明這個平行四邊形的面積是24平方厘米呢”這個問題。此問題一出，學生的研究視角聚焦到平行四邊形面積計算的細節中。而后，學生通過割補、數格子等方法，不但證明了這個平行四邊形的面積是24平方厘米，也印證了方法②的錯誤，并得到初步猜想“平行四邊形的面積可以用底×高來算”。

數學教學中，立于高位去設計教學路徑，用大問題統領教學，是促進學生數學思維萌芽、主動建構知識的關鍵步驟。

（二）大問題推進，促數學思維生長

教學時，引領學生走進平行四邊形面積計算問題本質后，學生的思路瞬間被打開，觀點呼之欲出。學生得到初步猜想“平行四邊形的面積可以用底×高來算”后，周衛東老師適時拋出問題“所有平行四邊形的面積都可以用底×高來計算嗎”。這個問題是引導學生由個體向類別推理的核心問題，課堂上，周衛東老師給學生提供了三個大小、形狀各不同的平行四邊形，讓學生通過割補等方法去印證自己的猜想。

在上述三個平行四邊形面積推導的過程中，學生進一步明確了之前的猜想，并且形成了基本的結論。一個又一個大問題推進的過程，就是學生數學思維不斷調整、整合、進階的過程。

（三）大問題歸納，促數學思維扎根

大問題屬于上位問題，是統整整個知識點乃至知識體系的問題，基于高觀點下的數學課堂，在大問題引領、推進之后，要有大問題歸納總結。在本節課中，雖然學生通過不完全歸納，經歷了“一個”到“一類”的認知過程，但是，周衛東老師并未就此引出平行四邊形面積計算公式，而是給學生布置了關鍵性任務——（1）觀察：轉化前后，兩個圖形有什么聯系？（2）推理：平行四邊形的面積為什么可以用底×高來計算？

教師在引領學生完成這個學習任務的過程中，引導學生學會推理歸納，進一步厘清平行四邊形面積計算的本質問題，即沿著平行四邊形的任意一條高剪開，拼成一個長方形，發現拼成的長方形的長等于平行四邊形的底、長方形的寬等于平行四邊形的高，且面積不變。所以，根據長方形的面積=長×寬，推導出平行四邊形的面積=底×高。

通過大問題的歸納總結，可以幫助學生厘清知識本質，養成從高位視角看待所學知識的素養，從而將學生的思維引向深入。

二、結構化關聯，促進學生主動建構知識

周衛東老師認為：“高觀點視角下的小學數學教學還應該能看到知識內在的結構。學科之所以為學科，不是簡單概念與知識要點的堆砌，其中非常重要的原因就在于學科知識之間存在著不可割裂的內在聯系。”數學常常被稱為“結構的科學”，是一種整體的、系統與意義的結構。知識學習走向結構化，才能更深刻地促進學生對知識的認知與理解。關聯主義學習理論認為，學習是對知識網絡結構中某種關系和節點的重新建構，是一個知識的連接過程。基于高觀點視角的數學教學，更應注重知識間的關聯，將學生的思維引向整體化、結構化的高度，促進學生主動建構知識。

（一）關聯在思維行進中

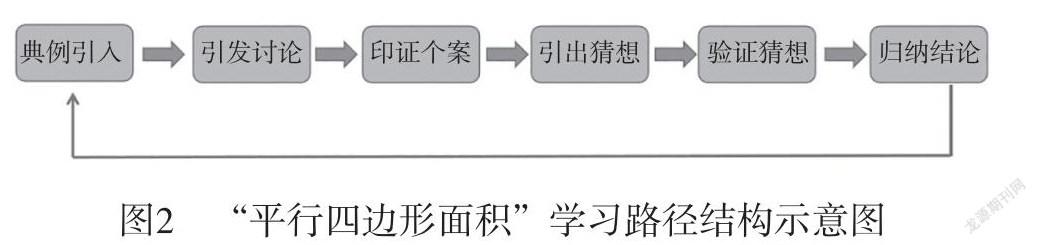
數學學習中，學生的思維行進呈現一個螺旋上升、逐步遞進的過程。因此，在教學時，教師應當在學生的思維行進過程中，做好生生互動的關聯、師生互動的關聯、學生與學材互動的關聯、學生與空間環境等互動的關聯。教師適時地引領和點撥，可以幫助學生掃清思維行進中的障礙，逐步建構知識。周衛東老師在執教“平行四邊形的面積”一課時，注重在學生思維行進中做好結構關聯。

從圖2中可以看出，周衛東老師順應了學生思維發展的脈絡，遵循了學生“學”的邏輯，使各個學習環節環環相扣、相互關聯，串起了整個知識學習的體系，使之結構化、系統化。

（二）關聯在思維困頓處

學生在思維進階的節點上可能會出現困頓。教師在教學中，設計學習任務時要預設到學生思維可能出現的困頓之處，通過引導，幫助學生加深對知識的理解，主動建構完整的知識體系。

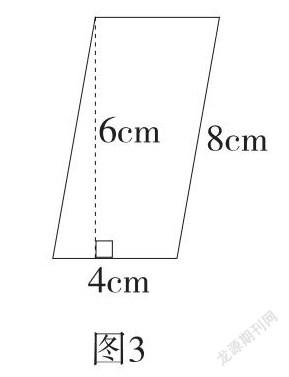
周衛東老師在執教“平行四邊形的面積”一課時，出示了這樣一道題：

師：如圖3，這個平行四邊形的面積怎么算？

生：用4×6來計算，答案是24平方厘米。

師：想一想為什么用“4×6”，而不用“8×6”呢？

生：因為平行四邊形的面積公式是底×高，所以要用“4×6”。

師：8厘米也是底啊，為什么不能用“8×6”來計算呢？

生：因為6厘米不是8厘米上的高，計算時要找到對應的高。

師：原來，計算平行四邊形面積時，要找到對應的底和高來計算。

計算平行四邊形面積時，學生往往只記住“底×高”，而忽視了“對應”這個關鍵要素，導致計算錯誤，形成認知錯位。周衛東老師在學生學習的困頓之處，通過實際問題，巧妙地將“對應”的底和高相乘的核心知識傳遞給學生，通過這樣的學習，真正將知識關聯互通，形成正確的認知結構。

（三）關聯在思維進階時

“高觀點”視角下的數學教學，不僅是引導學生將知識羅列堆砌，而且要將學生的思維引向更高的層次，建構新的知識體系。因此，學習任務的編排設計需要關聯學生思維進階的節點，為學生思維的順利進階提供必要的支持與幫助。周衛東老師在執教“平行四邊形的面積”一課時，立于“高觀點”之下，不僅關注學生當下知識的學習，還關注現在與未來知識之間的聯系。

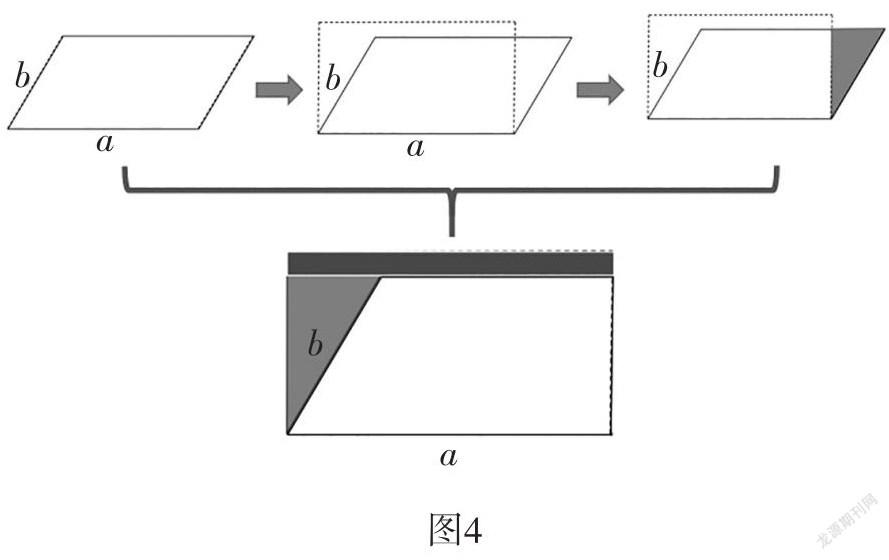
在回溯課前出示的方法②時，周衛東老師通過動畫演示的方法（如圖4），讓學生明白為什么不能用鄰邊相乘的方法來計算平行四邊形的面積。

從動態演示的過程可以看出，把平行四邊形拉直后，形成的長方形的面積比原來的圖形面積多了一塊。學生在動畫演示的過程中，進一步明確了，當平行四邊形的底和周長不變時，隨著高的增大，面積越來越大，一直到轉化為一個長方形時，面積最大。這樣的思維進階過程，通過動態演示，自然而然地印刻在學生的腦海中，學生形成了對平行四邊形面積計算的完整清晰的認知結構。

課行至此，思維進階并未停止，在高觀點視角下，周衛東老師進一步引領學生思考，如果將平行四邊形的鄰邊的角度標出，隨著角的傾斜變化，高也在不斷變化，從而將初中時將要學習的平行四邊形的計算公式向學生滲透，即平行四邊形的面積等于兩組鄰邊的積乘以夾角的正弦值。

學習至此，用周衛東老師的話來說：“此時，在學生的認知結構中，若隱若現留下的，是知識的全貌，是結構的雛形，更是朝向未來知識世界的美好。”什么是好的數學課堂？好的數學課堂就是將學生的思維引向深遠，讓學生帶著疑問走進課堂、帶著收獲和新的疑問走出課堂，形成數學學習螺旋上升的學習場。高觀點視角下的數學教學，通過關聯性的學習任務，將學生的思維引向更扎實、更高階的境界，從而讓學生主動建構知識體系、完善認知結構，培養數學核心素養，提升數學學習力。

三、思想性包攝，促進學生主動建構知識

周衛東老師在《試談高觀點視角下的小學數學教學》一文中指出：“高觀點視角下的小學數學教學應該能看到知識深層的思想方法。學科思想是學科知識中的‘隱性內容’，是學科專家提出的對學科發展和學科學習最具影響力的那些觀念和見解，是知識‘背后’的知識，是學科的精髓與靈魂。”周衛東老師在執教“平行四邊形的面積”一課時，將數學思想的滲透學習貫穿全課。

（一）由“個”到“類”，滲透歸納思想

上課伊始，周衛東老師說過這樣一句話：“周老師更加關注你們說明時使用的數學方法。”在引導學生探究平行四邊形的面積公式時，他先引導學生用“割補法”“數格子法”等方法去印證“一個”平行四邊形的面積可以用“底×高”來計算，進而引導學生進一步印證“任意”平行四邊形的面積都可以用“底×高”來計算。在由“個”到“類”的印證過程中，向學生滲透了不完全歸納的思想。

（二）由“新”到“舊”，滲透轉化思想

周衛東老師在帶領學生復習了之前學習過的平面圖形的面積計算方法，尤其是長方形的面積計算方法后，展示學生課前小研究中呈現的三種典型算法。學生在討論為什么方法③是對的時，想到了通過割補法，將平行四邊形轉化為長方形。將“新知”轉化為“舊知”，從而順利推導出平行四邊形面積的計算公式。且在轉化過程中，立意于高觀點，周衛東老師并未將學生的起點定位于實際操作，而是引導學生通過用“手”比畫、用“腦”想象，既滲透了轉化的思想，又提升了學生的空間想象能力。

（三）由“同”到“異”，滲透對應思想

在學生探索出平行四邊形的面積可以用“底×高”來計算后，周衛東老師通過一道題，引發學生思考：為什么都是平行四邊形的底？為什么不能和給定的高相乘？從而引導學生思考“同”是底，卻“異”在高的不同上，因此，得出結論：計算平行四邊形面積時，必須用對應的底乘對應的高。在這樣辨析的過程中，滲透了對應的數學思想。周衛東老師在《高觀點、低結構、中溫度——一種新的教學視角》一文中指出：“從數學教學角度看，一堂課新往往就新在思維過程上，高往往就高在思想性上，好往往就好在學生參與活動的深度和廣度上。有思想深度的課，給學生留下長久的心靈激蕩和對知識的深度理解，以后即使具體的知識忘了，但數學地思考問題的思想方法卻將長久存在。”

在數學教學中，基于高觀點的視角，可以將學生的思維引向更扎實、更高階的境界，從而讓學生主動建構知識體系、完善認知結構，培養數學核心素養，提升數學學習力。

注：本文系江蘇省教育科學“十三五”規劃青年專項課題“指向主動建構的小學數學學習歷程案開發的研究”（課題批準號：C-c/2020/02/31）研究成果。