基于擴張狀態觀測器補償的Boost變換器無源控制

李史玉，李建國，張雅靜，王久和

（北京信息科技大學自動化學院，北京 100192）

為實現以“碳達峰、碳中和”為目標的能源結構轉型，新能源電動汽車、超級不間斷電源系統、通信基站，以及大型數據中心等分布式電源系統對變換器整體裝置的性能和穩定性提出了更為嚴苛的要求。在器件和拓撲結構一定的情況下，急需從控制策略角度提出改進系統性能的方法。

Boost變換器由于拓撲結構簡單、性能穩定，被廣泛應用于通信電源[1]、光伏系統、儲能系統[2]等領域。傳統Boost變換器通常采用比例積分PI（pro?portional integral）控制方法，由于傳統的PI控制是基于線性模型，大信號擾動工況系統動態性能差，難以保持系統穩定；而Boost變換器是非線性系統，將線性控制策略應用于非線性系統中存在局限性。國內外學者對非線性控制策略進行了大量的研究，并開始應用在電力電子變換器中，以提升系統動態性能。其中，滑模控制SMC（sliding mode control）以結構簡單、魯棒性強得到廣泛應用，但由于其本身控制律的離散特性，容易產生抖動，影響控制精度[3-4]。狀態反饋線性化通過適當變換，將非線性問題轉化成線性問題，但要求系統模型非常精確，設計的控制律較為復雜，不利于工程實現[5]。文獻[6]通過設計電路參數或控制器參數來滿足無源性穩定判據，從而保證系統穩定性，但本質上仍然是線性控制。

無源控制PBC（passivity-based control）作為非線性控制策略的一種，其本質是一種能量控制，可實現系統的全局穩定，動態性能良好，已經應用到許多領域[7]。文獻[8-10]分別通過對Boost變換器、單相PWM電壓源變換器、Cuk變換器進行PBC控制，從而實現輸出的穩定。

在寄生電阻或其他未知擾動的影響下，最終的電壓輸出會存在穩態誤差[11]。如何消除Boost變換器受到未知擾動產生的穩態誤差，是Boost變換器無源控制需要解決的問題[12]。目前，常用的解決方案是在無源控制的基礎上增加外環控制來消除誤差。文獻[13]對于儲能變換器，電流內環采用無源控制，電壓外環采用滑模控制，來補償內環電流精度；文獻[14]在無源控制基礎上，外環引入PI控制器來消除靜態誤差。雙環控制增大了系統結構的復雜程度。擴張狀態觀測器ESO（extended state ob?server）可以在系統信息較少的情況下對擾動進行動態估計與反饋補償[15-16]，從而確保系統穩定，提高系統的魯棒性和抗干擾能力[17-19]。

針對Boost變換器受到未知擾動時存在穩態誤差的問題，本文提出一種基于擴張狀態觀測器的無源控制策略。首先，對Boost變換器建立歐拉-拉格朗日EL（Euler-Lagrange）模型，采用阻尼注入的方法設計了無源控制器，并進行參數整定。然后，基于擴張狀態觀測器來對未知擾動進行觀測和補償，以消除系統穩態誤差。最后，搭建基于擴張狀態觀測器補償的無源控制仿真模型，仿真結果表明，本文所提控制策略可以補償系統因未知擾動造成的穩態誤差，提高系統的動態性能。

1 數學模型與無源控制器

1.1 數學模型與無源性分析

寄生電阻廣泛存在于開關、電感等元件中，含有寄生電阻的Boost變換器電路如圖1所示。其中，us為直流電源輸入電壓；L為電感器電感；VT為開關管；VD為二極管；C為電容器電容；R為負載；iL為流過電感器L的電流；uC為電容器兩端電壓；RL、RVT、RVD分別為電感器、開關管VT、二極管VD的寄生電阻。

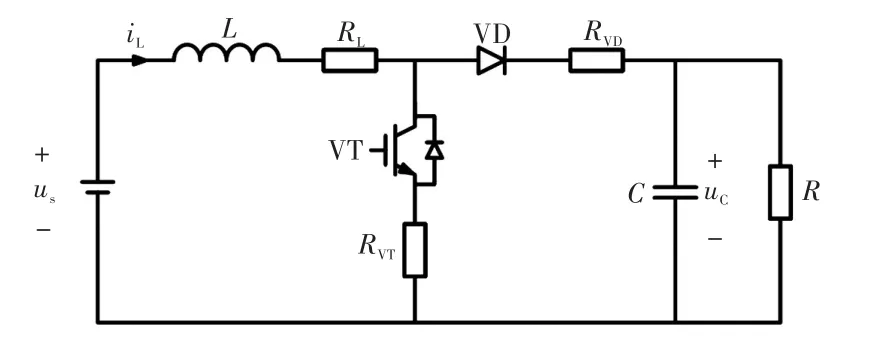
圖1 含有寄生電阻的Boost變換器電路Fig.1 Boost converter circuit with parasitic resistance

1.2 無源控制器設計

1.3 無源控制器參數選取

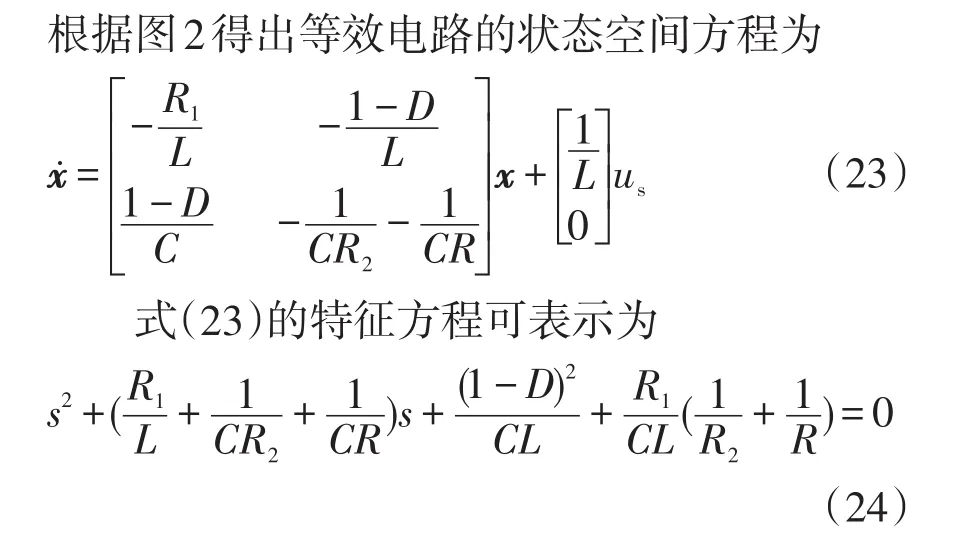
由式（18）可以看出，電感存儲能量與Ra1有關，電容存儲能量與Ra2有關。為了選擇阻尼注入Ra的值，建立圖2所示的Boost變換器等效電路。圖2中，R1為電感器串聯電阻；R2為電容器串聯電阻。

圖2 無源控制下的Boost變換器等效電路Fig.2 Equivalent circuit of Boost converter under PBC

分別取阻尼比ξ為 0.1、0.5、1.0、1.5、2.0，此時閉環系統在單位階躍信號作用下的輸出電壓響應如圖3所示。由圖3可以看出，當0<ξ<1即系統處于欠阻尼狀態時，系統的瞬態響應呈現幅值按指數規律衰減的正弦振蕩曲線；當ξ=1或ξ>1即系統處于臨界阻尼或者過阻尼狀態時，系統的瞬態響應呈現為一條單調上升的指數曲線，沒有振蕩發生，因此無源系統更穩定。此時

圖3 系統的單位階躍響應曲線Fig.3 Unit step response curve of system

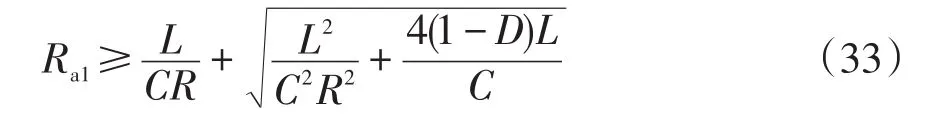
結合L、C參數，本文選擇Ra1=5。

圖4為系統在不同阻尼比時對應的伯德圖，由圖4可以看出，曲線阻尼比從左到右依次增大，對應的相位裕量均大于零，并且逐次增大。

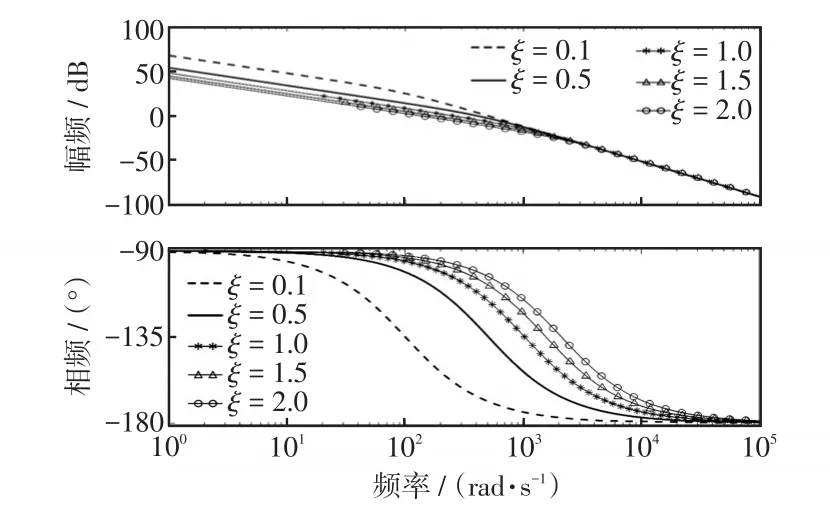
圖4 引入虛擬阻尼Boost變換器的伯德圖Fig.4 Bode diagram of Boost converter with virtual damping

2 擴張狀態觀測器設計與參數選取

2.1 擴張狀態觀測器設計

本文利用ESO對擾動項dis進行估計，將觀測得到的未知擾動在系統輸入端進行補償，進而消除寄生電阻對系統帶來的影響。

將理想占空比減去擾動對應的占空比即在輸入端對擾動進行了補償，得到最終控制量來消除寄生電阻對變換器造成的影響。系統控制框圖如圖5所示，由圖5可知，無源控制器以us、iLav、uCav、和為輸入信號，利用ESO對擾動進行補償，經過簡單的運算后輸出實際占空比，通過PWM發生器，產生PWM波，驅動開關管來達到控制的目的。

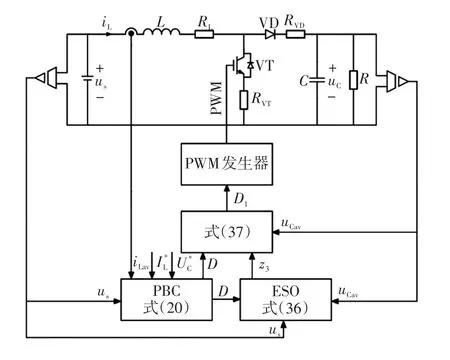
圖5 系統控制框圖Fig.5 Control block diagram of system

2.2 擴張狀態觀測器參數選取

通常，增大β01可以加快系統的響應速度，縮短過渡時間；增大β02可以抑制超調量；增大β03可以加快誤差追蹤速度。對于fal函數中的參數α與δ來說，α一般取值為0～1之間的常數。α減小，跟蹤速度變快，濾波效果變差；δ增大，濾波效果變好，跟蹤速度變慢。依據穩定約束條件和參數整定的原則，選取相關參數如表1所示。

表1 ESO參數Tab.1 ESO parameters

3 仿真結果

本文基于PSIM仿真軟件對所提出的Boost變換器的控制策略進行仿真驗證。電路仿真參數如表2所示。

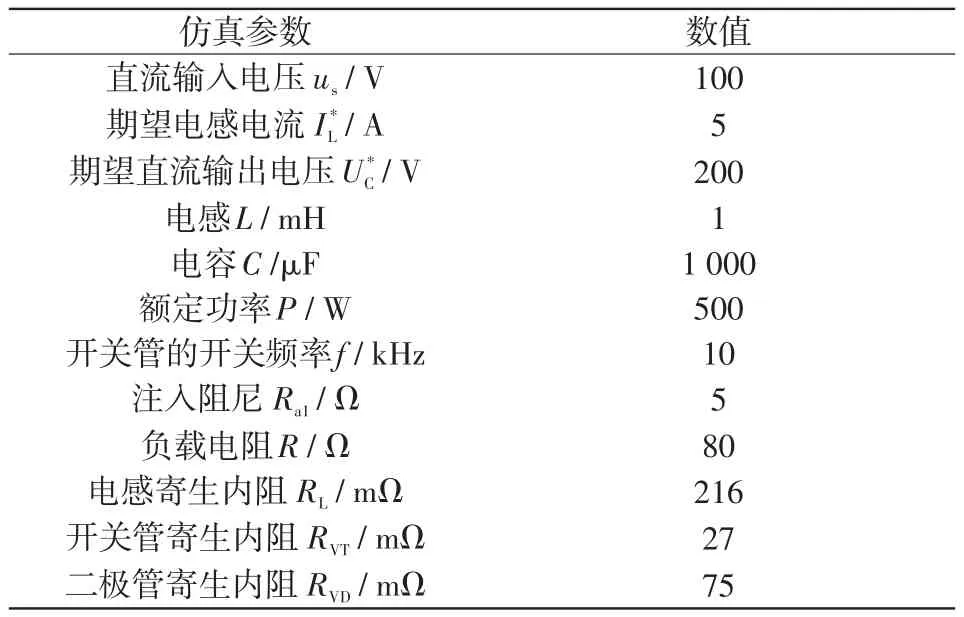
表2 變換器參數Tab.2 Converter parameters

3.1 未知擾動仿真

將系統內部寄生電阻和輸出負載的變化作為未知擾動，圖6為未知擾動下輸出電壓波形。圖6（a）為改變RL后輸出電壓的波形，圖6（b）為其局部放大圖。在1 s時，RL由216 mΩ減小為200 mΩ，由圖6（a）和（b）可以看出，輸出電壓在0.09 s時達到穩態，穩定之后輸出電壓達到期望值200 V，穩態紋波為0.128 V；ESO可以補償由寄生內阻帶來的穩態誤差，改變寄生電阻后，輸出電壓波形沒有明顯變化，仍然可以達到期望值。圖6（c）為改變R后輸出電壓的波形，圖6（d）為其局部放大圖。在1 s時，R由80 Ω增大為100 Ω，此時功率由500 W減小為400 W，保持200 V不變。由圖6（c）和（d）可以看出，輸出電壓在0.09 s達到穩態，在改變輸出負載后，輸出電壓有較小波動，電壓變化幅度為0.122 V；穩定之后又達到期望值200 V，穩態紋波為0.106 V，從而驗證ESO可以有效抑制未知擾動。

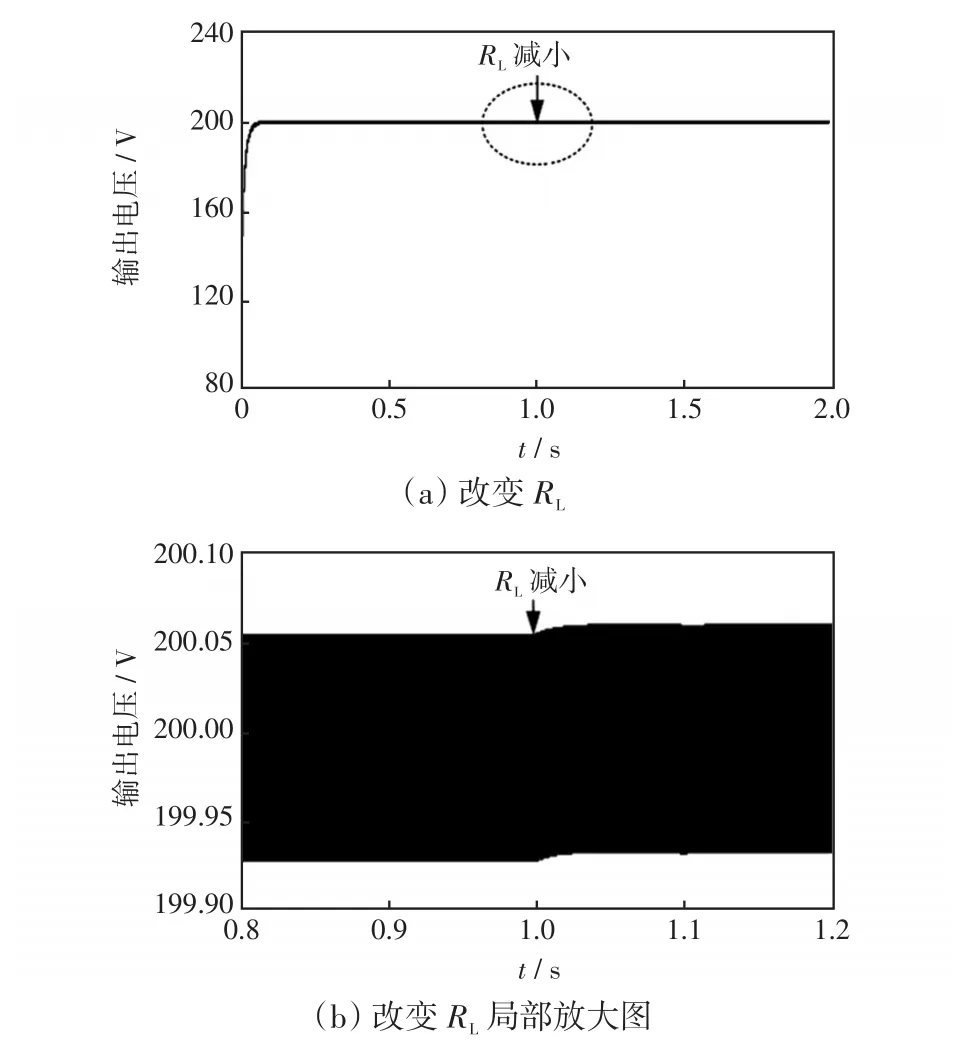
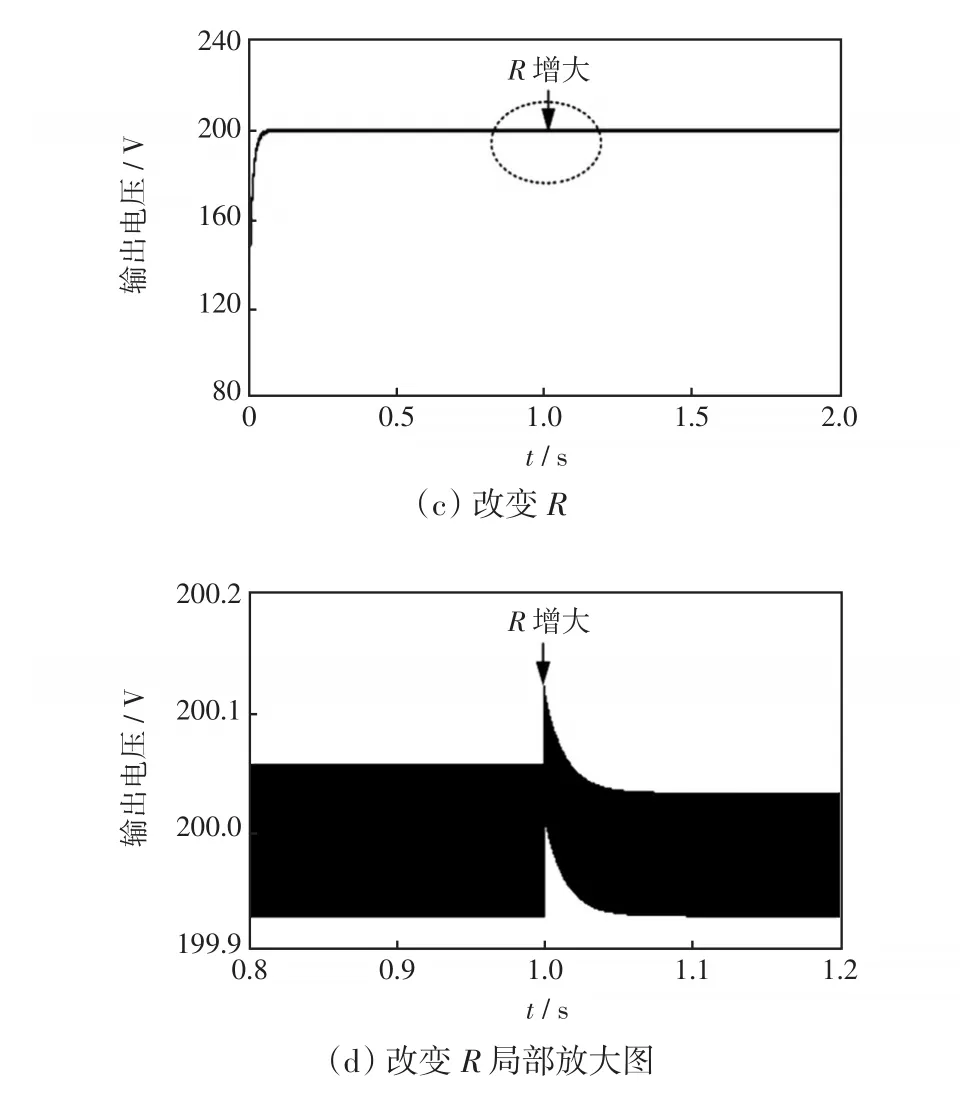
圖6 未知擾動下的輸出電壓Fig.6 Output voltage under unknown disturbance

3.2 動態性能仿真

通過改變系統輸入輸出電壓期望值，可以得出系統對設定值跟蹤的動態性能表現，圖7為系統動態跟蹤性能波形圖。圖7（a）為改變us的輸出電壓波形，圖7（b）為其局部放大圖。在1 s時，輸入電壓由100 V增加到105 V，保持功率500 W不變，I*L由5 A減小為4.762 A，U*C保持200 V。由圖7（a）和（b）可以看出，輸出電壓在0.09 s達到穩態；改變輸入電壓，輸出電壓有較小波動，電壓變化幅度為0.073 V，穩定后達到200 V，穩態紋波為0.126 V。圖7（c）為由200 V減小為160 V的輸出電壓波形，圖7（d）為其局部放大圖。由圖7（c）和（d）可以看出，輸出電壓在0.09 s達到200 V并穩定；當1 s時減小，輸出電壓經0.06 s后恢復穩態達到160 V，穩態紋波為0.080 V。輸出電壓的動態響應速度較快，沒有超調，穩態時也沒有穩態誤差。

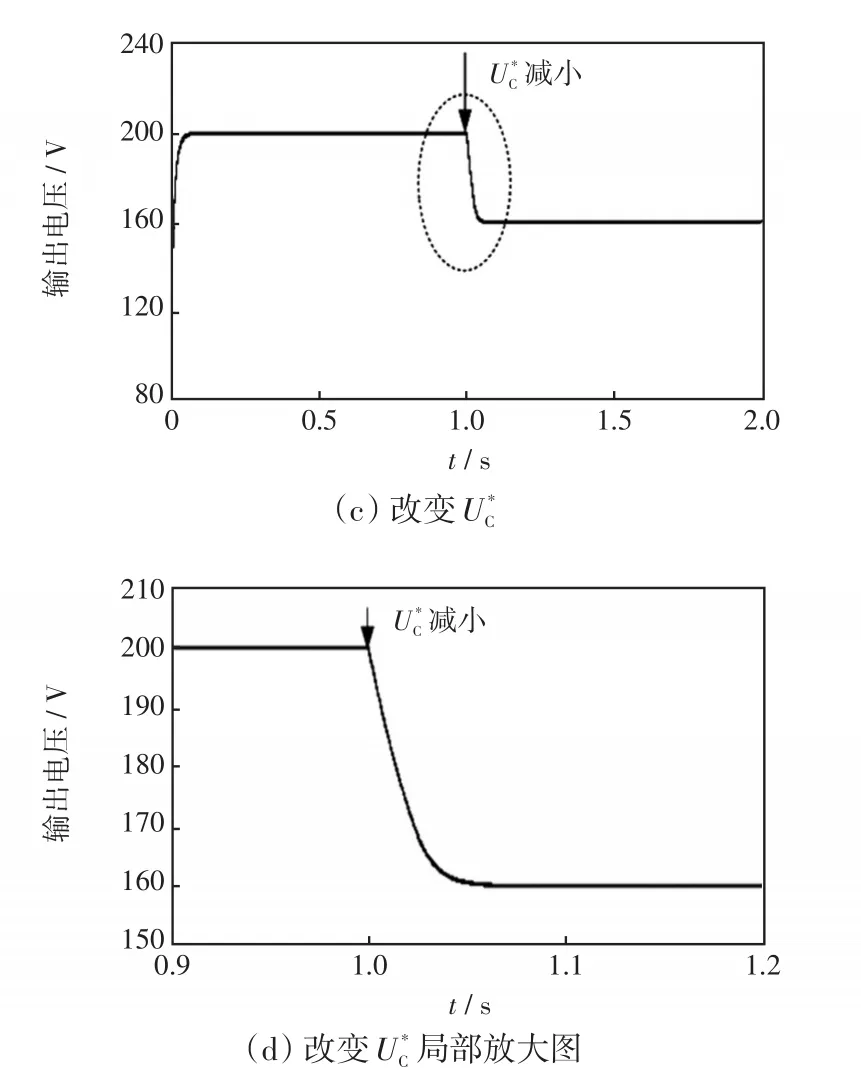
圖7 動態跟蹤性能波形Fig.7 Waveforms of dynamic tracking performance

3.3 多種控制策略仿真

將PBC+ESO控制、PBC控制、PI控制3種控制策略同時進行仿真比較。圖8（a）為3種控制策略下輸出電壓波形，圖8（b）和（c）為其局部放大圖。在1 s時，將由200 V減小到180 V，功率由500 W減小為405 W，由5 A減小至4.05 A。表3為不同控制策略下輸出電壓性能指標。其中，ess1、ess2分別為在改變前、后的穩態誤差；δ為在改變后的超調量；tr1、tr2分別為啟動瞬間和改變瞬間到達穩態的時間。由圖8及表3可以看出，PBC+ESO控制相比于PBC控制有效抑制了由寄生電阻產生的穩態誤差。同時與PI控制相比可獲得更好的動態性能。

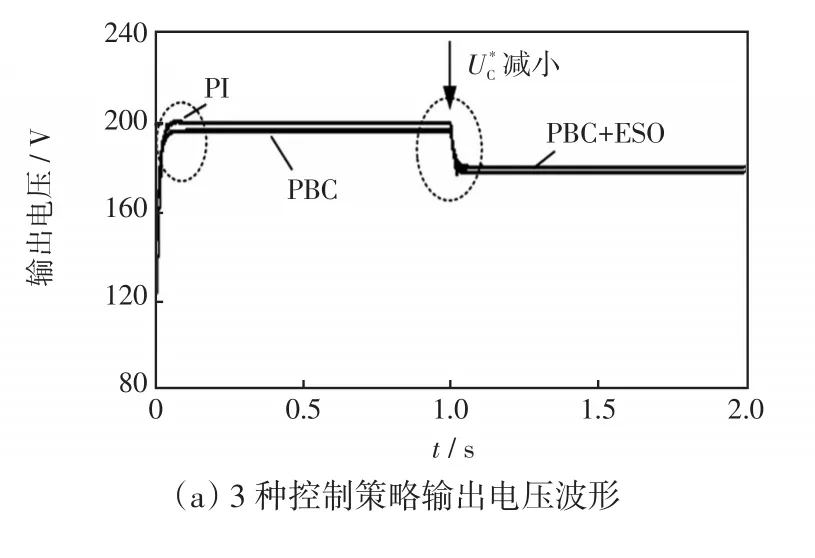
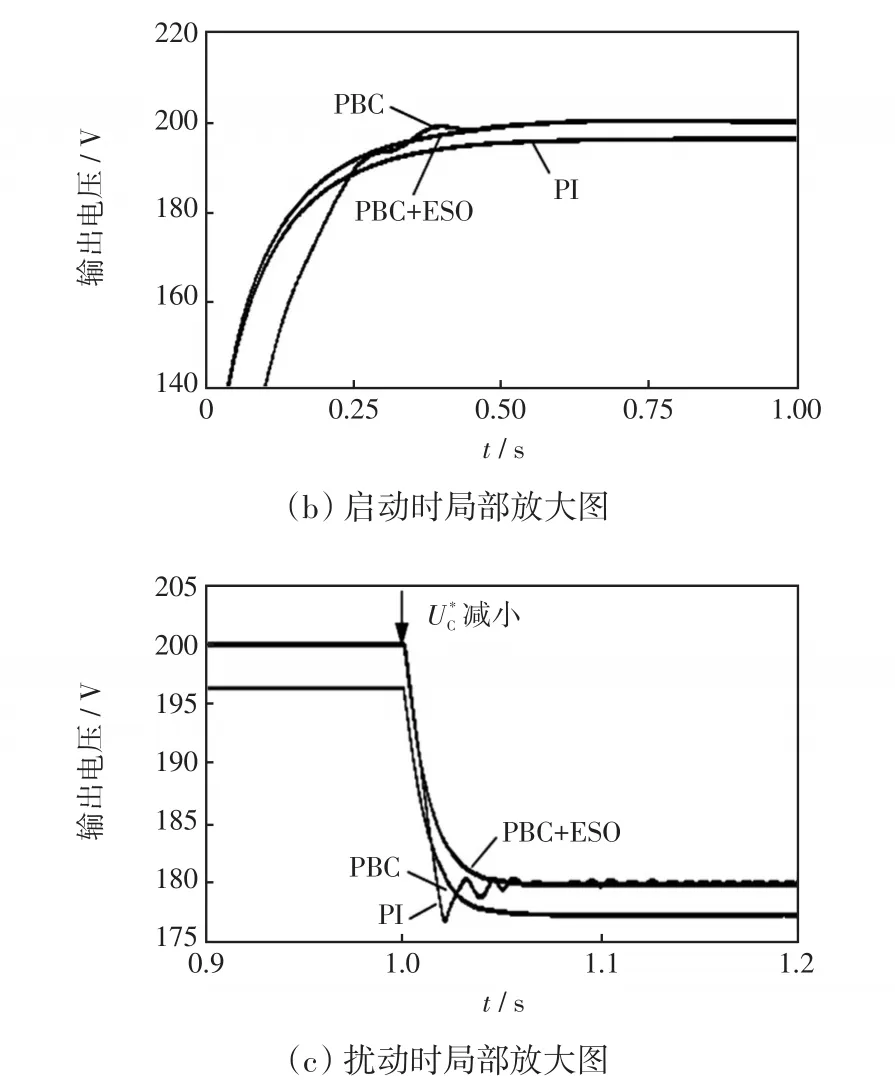
圖8 輸出電壓波形Fig.8 Waveforms of output voltage

表3 輸出電壓性能指標Tab.3 Performance indexes of output voltage

4 結語

本文建立了基于EL模型的Boost無源控制器，并針對系統的未知擾動，設計了擴張狀態觀測器。通過該擴張狀態觀測器，對無源控制在系統內部存在寄生參數或受到外部擾動的情況下出現的穩態誤差進行補償，提高了系統的動態性能和穩態性能。通過仿真結果證明本文所提控制策略可以獲得較好的控制特性。