基于輻射噪聲干涉條紋斜率分布的聲源深度分辨方法研究

安 良 徐若珺 曹紅麗

①(東南大學水聲信號處理教育部重點實驗室 南京 210096)

②(東南大學信息科學與工程學院 南京 210096)

③(東南大學吳健雄學院 南京 210096)

1 引言

水中目標的航行或工作深度是其重要的屬性，也是進行目標類型判別的重要依據。被動聲吶作為水中非合作目標探測的重要手段之一，主要基于各種水聲被動定位方法，利用目標輻射(或發射)的聲信號進行目標深度估計。但是由于海洋環境的復雜性、目標信號先驗信息的缺失以及聲吶設備自身的限制，水中目標深度的準確估計仍是水聲被動定位的難題之一。

相比于聲源深度的估計，對水面目標(深度較小)和水下目標(深度較大)進行雙擇假設判決，可為目標類型判斷提供依據，對于水下威脅目標的探測識別有重要的意義。聲源的深度與簡正波各階模態的分布密切相關，現有方法大多基于簡正波理論，利用聲源深度與簡正波模態之間的對應關系實現聲源深度的二元判決。

匹配場處理被廣泛應用于水聲被動定位，也是研究人員最為關注的深度判別方法。楊坤德等人[1]提出基于環境擾動的線性匹配場處理方法，通過增加環境擾動約束提高方法在隨機誤差下的穩健性，但方法在目標方位與干擾方向相似時失效。王奇等人[2]提出基于最小二乘算法短垂線陣匹配場處理技術的目標深度辨別方法，用最小二乘得到各階模態系數估計值重構短垂線陣測量場向量，提高了短垂線陣匹配場處理性能，但其性能在聲場采樣不充分時下降。Yang[3]提出基于數據的窄帶信號移動源深度辨別方法，利用垂直陣接收數據提取深度函數以降低環境依賴性，但方法穩健性較低。Lin等人[4]提出基于單水聽器匹配場的目標源深度辨別方法，利用頻差波束形成器通過降頻減小實際與模型的不匹配性，但其性能在環境變化時下降。畢雪潔等人[5]提出以垂直復聲強無功分量為匹配量的目標深度匹配的二元分類方法，但方法對線譜頻率穩定性要求較高。張朝金等人[6]利用半經驗關系建立聯合匹配定位方法，實現爆炸聲源深度精確反演，但其在估計遠距離目標時性能下降。

基于簡正波分解的模式閃爍指數也常用于水下目標深度判別的依據。Premus等人[7,8]利用子空間投影法估計聲源模態譜的差異，提出利用水平線陣進行目標深度辨別的模式閃爍指數，但方法對水平孔徑有一定要求。近年來，Warping變換受到了眾多學者的關注。Li等人[9]利用Warping變換提取簡正波自相關與互相關指數解決波浪運動帶來的源深度變化問題，并提出模式相關閃爍指數的概念。劉志韜等人[10]提出基于簡正波相關項特征頻率間比例關系的聲源分辨方法，用Warping變換分離簡正波相關項，但是方法性能在負躍層情況時降低。

近年來對干涉條紋的研究蓬勃發展，其核心思想是利用波導不變量、干涉條紋、聲源徑向運動速度和距離之間的關系[11]，在聲場干涉結構中提取波導不變量，從而利用波導不變量的數值判別聲源深度，但是這種方法需要在聲源和接收器相對距離已知的條件下[12-14]。也有學者探究未知相對位置條件下波導不變量的提取：劉志韜等人[15]利用目標時延軌跡計算波導不變量，但方法要求聲源相對于水聽器近似勻速運動；蘇冰等人[16]提出一種波導不變量β譜分離算法估計聲源距離和波導不變量，但是方法只適用于波導不變量值隨頻率變化緩慢的情況。

本文提出了一種利用輻射噪聲干涉條紋分布進行聲源深度二元判決的方法。在存在負躍層的淺海波導中，利用Radon變換從干涉圖像中提取干涉條紋斜率的分布，可以在未知聲源距離的情況下判別聲源深度。相比傳統波導不變量方法和匹配場法，不需要聲源距離與海洋聲學環境參數的先驗信息。

2 二元深度判別的基本原理

2.1 干涉條紋特征差異的物理機理

根據波導不變量理論[17]，聲場干涉條紋的波導不變量可用各簡正波相干項βmn加和描述。

根據文獻[19]，當接收點與聲源間距離足夠大時，條紋的斜率近似于波導不變量。根據式(3)計算統計量svarmn，可得ω∈[ω1, ω2]頻帶內βmn(ω)的分布情況。波導不變量為各階簡正波相干項βmn(ω)的疊加，按式(4)定義統計量γMN，可表征一定頻率范圍內波導不變量的分布情況，進而反映干涉條紋斜率的分布情況，其中M,N約束了參與相干疊加的簡正波的階數范圍。若γMN較小，干涉條紋斜率分布均一；若γMN較大，干涉條紋斜率分布不均。

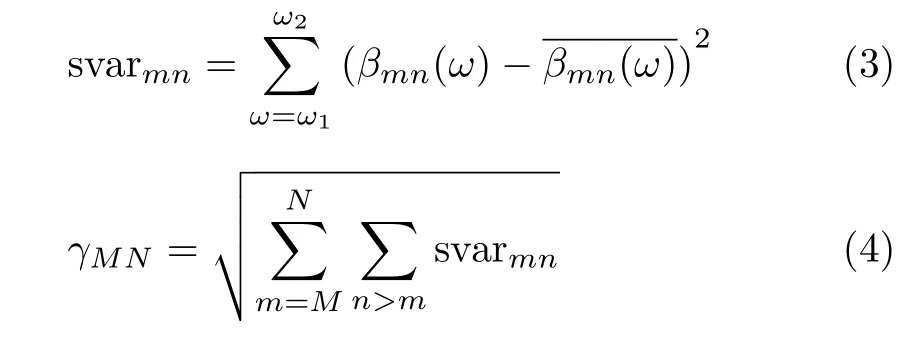
表1給出了在水深100 m，海水聲速1500 m/s，海水密度1.024 g/cm3，海底聲速1749 m/s，海底密度1.96 g/cm3的Pekeris波導條件下，信號頻率為250～350 Hz、頻率分辨率為1 Hz時聲源與接收器距離為5.0～6.6 km的各階簡正波相干項βmn(ω)的統計量svarmn。將表1數據代入式(4)計算得γ14=189.91, γ59=1818.57。低階簡正波間相干的得到的統計量γ較小，而較高階簡正波間的統計量γ較大，所以低階簡正波相干形成的干涉結構斜率分布均一，較高階簡正波相干形成的干涉結構斜率分布不均。

表1 頻率250～350 Hz各階簡正波相干項波導不變量的標準差svarmn

考慮有負躍層的典型淺海波導環境，聲速剖面如圖1所示，其中負躍層深度從15 m到35 m，對應聲速分別為1515.5 m/s和1485.5 m/s，海面聲速1520 m/s，近海底處水中聲速1482.25 m/s，海底聲速1759 m/s。

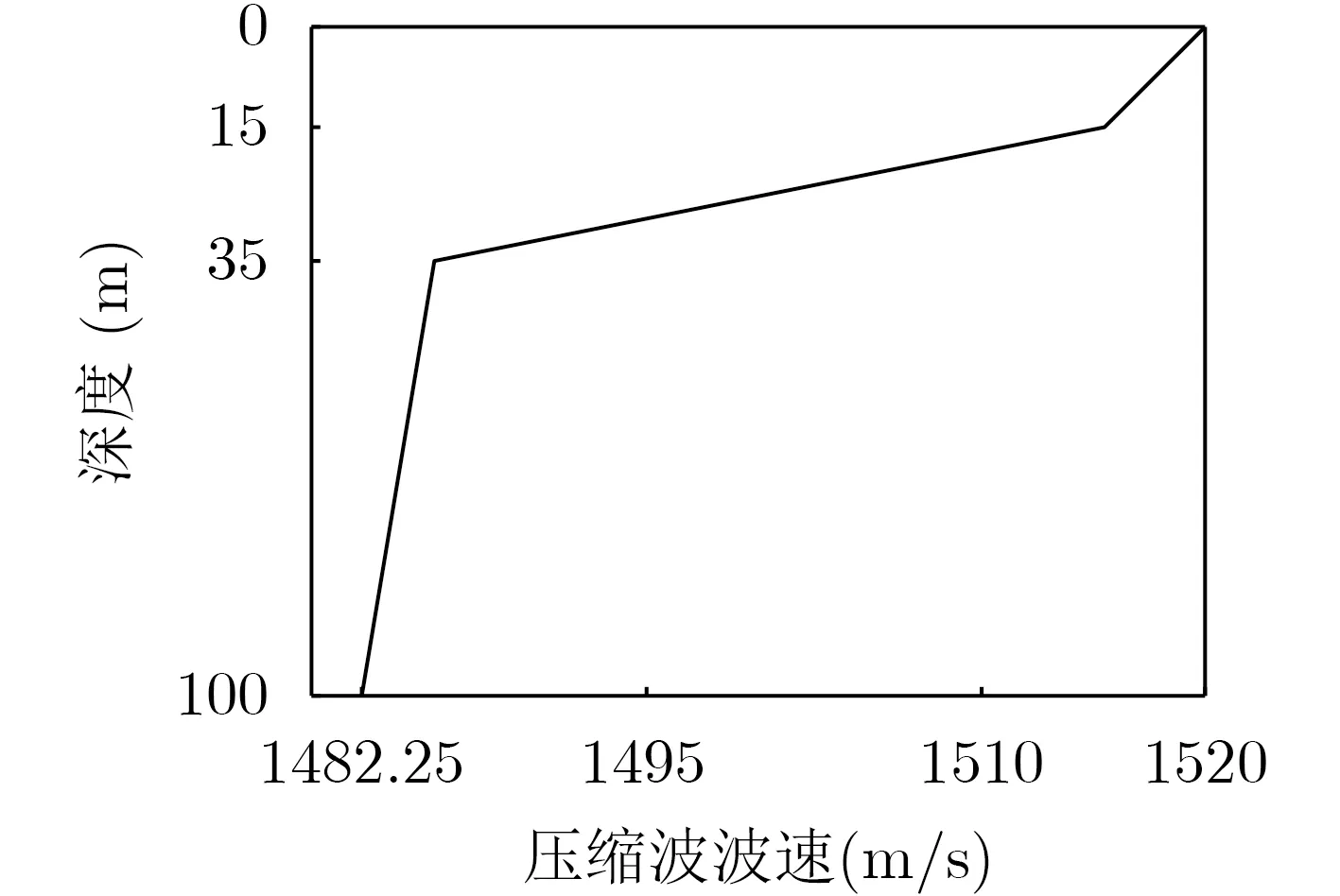
圖1 典型淺海聲速剖面

圖2給出了頻率為300 Hz，深度分別為10 m和35 m的聲源激發的前10階簡正波幅度值。可見，深度10 m的聲源(水面聲源)激發的低階簡正波幅度小，激發的較高階簡正波幅度大。深度35 m的聲源(水下聲源)低階簡正波與較高階簡正波都有激發。

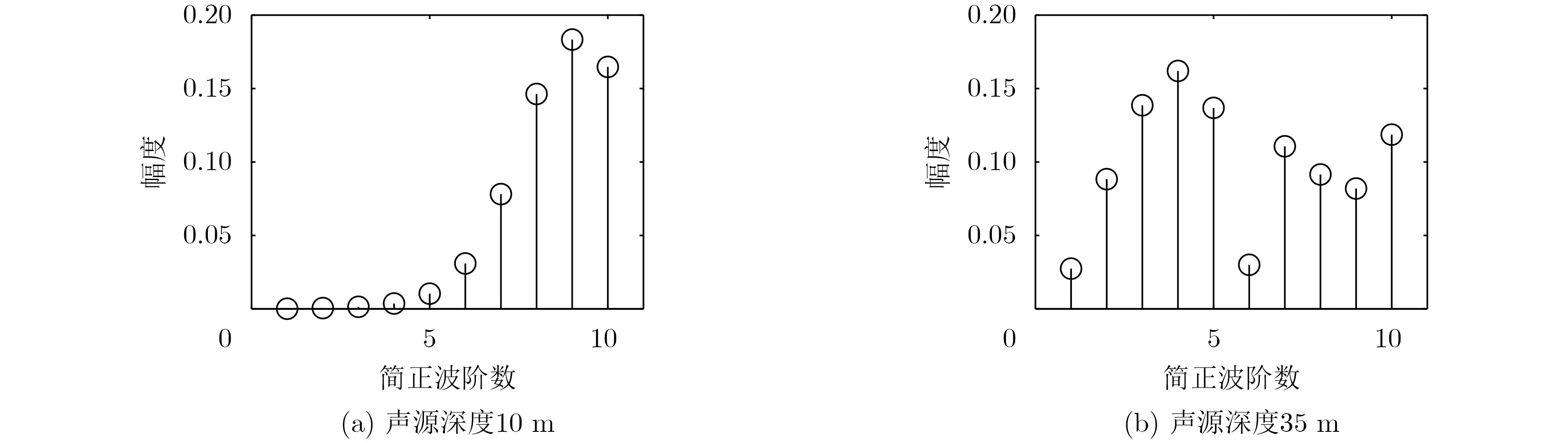
圖2 頻率300 Hz前10階簡正波幅度

根據前述干涉條紋斜率分布規律的分析，水面聲源較高階的簡正波占主導，所以干涉條紋斜率分布不均，水下聲源雖然同時激發了低階與較高階的簡正波，但經過遠距離傳播后較高階的簡正波衰減較大，低階簡正波能量占比較大[16]，所以干涉條紋斜率分布均一。

2.2 干涉條紋特征提取的理論解釋

由2.1節可知，聲源深度的差異性會引起干涉條紋斜率分布的差異性，接下來我們試圖量化這種差異性。Radon變換是一種投影方法，可以檢測圖像中的直線，定義為[20]

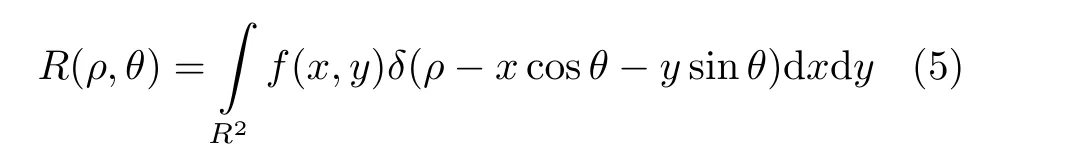
其中，f(x, y)是被積函數，x, y和ρ, θ分別為原視空間坐標和Radon空間坐標，δ(·)函數為狄利克雷函數，R(ρ, θ)為Radon變化后原函數在(ρ, θ)處的投影值。給定2維函數f(x, y)定義如下，其中ak, bk, ck為常數。

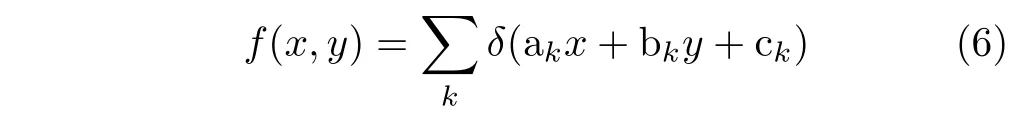
將式(6)代入式(5)，設x取值[x1,x2]，y取值[y1,y2]，Radon變換表達式可寫成

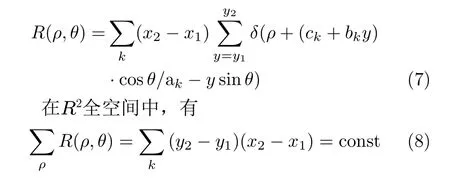
設式(7)中k = 1，當tanθ ≠ b1/a1時，對于方程 δ(ρ+(c1+b1y)cosθ /a1-y sinθ) = 1，任意ρ都有y使得方程成立；tanθ = b1/a1時，當且僅當ρ = -c1cosθ/b1時方程成立。則可設

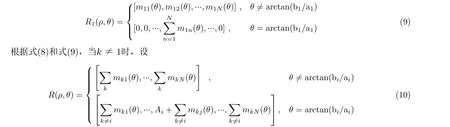
結合式(12)，當bi/ai均相同時，即空間中存在有限多相同斜率的直線，序列z(θ)有單個或較少峰值；當bi/ai不同時，即空間中存在有限多不同斜率的直線，序列z(θ)有較多峰值。定義Radon變換角度為0～180°，步長為0.1°，由式(12)計算z(θ)，結果如圖3所示，圖3(a)、圖3(c)是Radon變換前圖像，圖像像素為300×300，其中圖像的寬度方向對應圖中x坐標，高度方向對應圖中y坐標；圖3(b)、圖3(d)是z(θ)曲線，其橫坐標為Radon變換角度，縱坐標為歸一化后的z(θ)值。圖3(b)、圖3(d)可知，空間中直線斜率分布均一時，z(θ)為單峰或較少峰值；空間中直線斜率分布不均時，z(θ)為多峰值。由此，干涉條紋斜率的分布情況可由Radon變換后列方差向量的峰值個數表征，列方差向量z(θ)計算方法由式(12)給出。

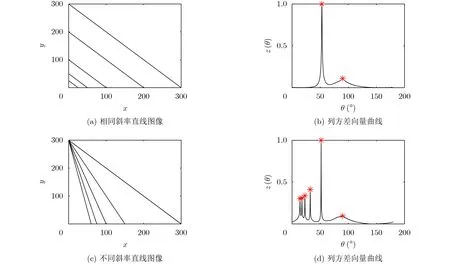
圖3 Radon變換后列方差向量曲線

分析可知，列方差向量曲線的峰值個數與干涉條紋斜率的分布有關，其取決于參與干涉的簡正波階數，而參與干涉的簡正波階數與負躍層的聲速梯度和聲源深度密切相關。因此，可以考慮將列方差向量曲線的峰值個數作為聲源深度判別的依據。

2.3 聲源深度判別方法

結合2.1節、2.2節，若輻射噪聲干涉條紋呈現多種斜率，Radon變換后列方差向量為多個峰值；若輻射噪聲干涉條紋呈現單一斜率，Radon變換后列方差存在較少峰值。考慮與圖1相同的水文環境，選取信號分析的頻率范圍為200～500 Hz，頻率分辨率為1 Hz，假設在分析信號頻帶內聲源信號為白噪聲，接收器深度為5 m，聲源深度分別為10 m(水面聲源)和35 m(水下聲源)，聲源與接收器距離為5.0～6.6 km，距離采樣間隔為1 m，利用Kraken模型仿真得到輻射噪聲干涉條紋如圖4所示。

圖4給出了不同深度聲源輻射噪聲干涉條紋，其條紋斜率分布的均一性不同。利用Radon變換處理條紋圖像，將變換后矩陣按式(12)求得列方差向量，得向量的峰值個數如圖5所示，水面、水下目標的峰值個數分別為4個和2個，水面目標的峰值個數多于水下目標。

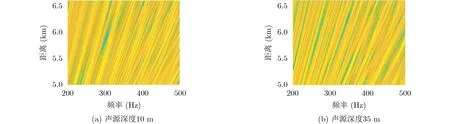
圖4 不同深度聲源輻射噪聲的干涉條紋圖像

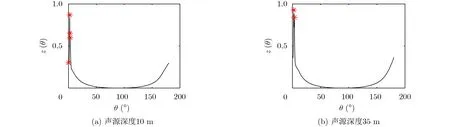
圖5 Radon變換后列方差向量曲線

由前文分析可知，峰值個數與負躍層聲速梯度的大小有密切聯系，本文選取另兩種有負躍層的典型淺海波導環境[21]，通過仿真分析負躍層梯度大小對峰值個數的影響。負躍層深度從15 m到35 m。兩種環境中，15 m處聲速分別為1510.5 m/s和1520.5 m/s，負躍層梯度分別為1 s-1和2 s-1，海面聲速分別為1515 m/s和1525 m/s，近海底處聲速分別為1487.25 m/s和1477.25 m/s，海底聲速為1759 m/s。

圖6和圖7給出了負躍層梯度分別為-1 s-1和-2 s-1時聲源信號的干涉條紋與Radon變換后的列方差向量曲線。在負躍層梯度不同時，水面水下目標噪聲干涉條紋Radon變換后的列方差向量曲線峰值個數有微小變化，如梯度為-1 s-1時，水面和水下聲源對應的峰值個數分別為3個和2個；梯度為-1.5 s-1時，水面和水下聲源對應的峰值個數分別為4個和2個；梯度為-2 s-1時，水面和水下聲源對應的峰值個數分別為4個和2個。聲速剖面負躍層梯度的大小對分辨門限的影響較小。在本文后續的研究，門限值默認選取為3，即當列方差向量曲線峰值個數不小于3個時，判別對應的聲源為水面聲源，反之判別為水下聲源。

圖6 負躍層梯度為-1 s-1時輻射噪聲干涉條紋圖像及列方差向量曲線

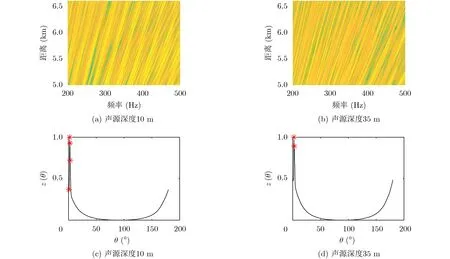
圖7 負躍層梯度為-2 s-1時輻射噪聲干涉條紋圖像及列方差向量曲線

在實際海洋信道中，接收的目標信號中不可避免地會疊加環境噪聲。由于海洋環境噪聲級在低頻段變化緩慢[22]，本文為了便于干涉特性分析，假設環境噪聲在信號分析頻帶范圍內也為白噪聲，其余參數與圖4和圖5中參數一致。圖8、圖9和圖10分別給出了信噪比為0 dB, 5 dB和10 dB時，含有環境噪聲的聲源信號干涉條紋與Radon變換后的列方差向量曲線。如圖，由于環境噪聲的影響，水面水下目標輻射噪聲干涉條紋Radon變換后的列方差向量曲線峰值個數差異性減小：信噪比為0 dB時，水面和水下聲源對應的峰值個數分別為2個和2個；信噪比為5 dB時，水面和水下聲源對應的峰值個數分別為3個和2個；但在信噪比為10 dB時，水面和水下聲源對應的峰值個數分別為4個和2個，對辨別結果影響較小。本文后續的仿真，暫不考慮環境噪聲的影響。

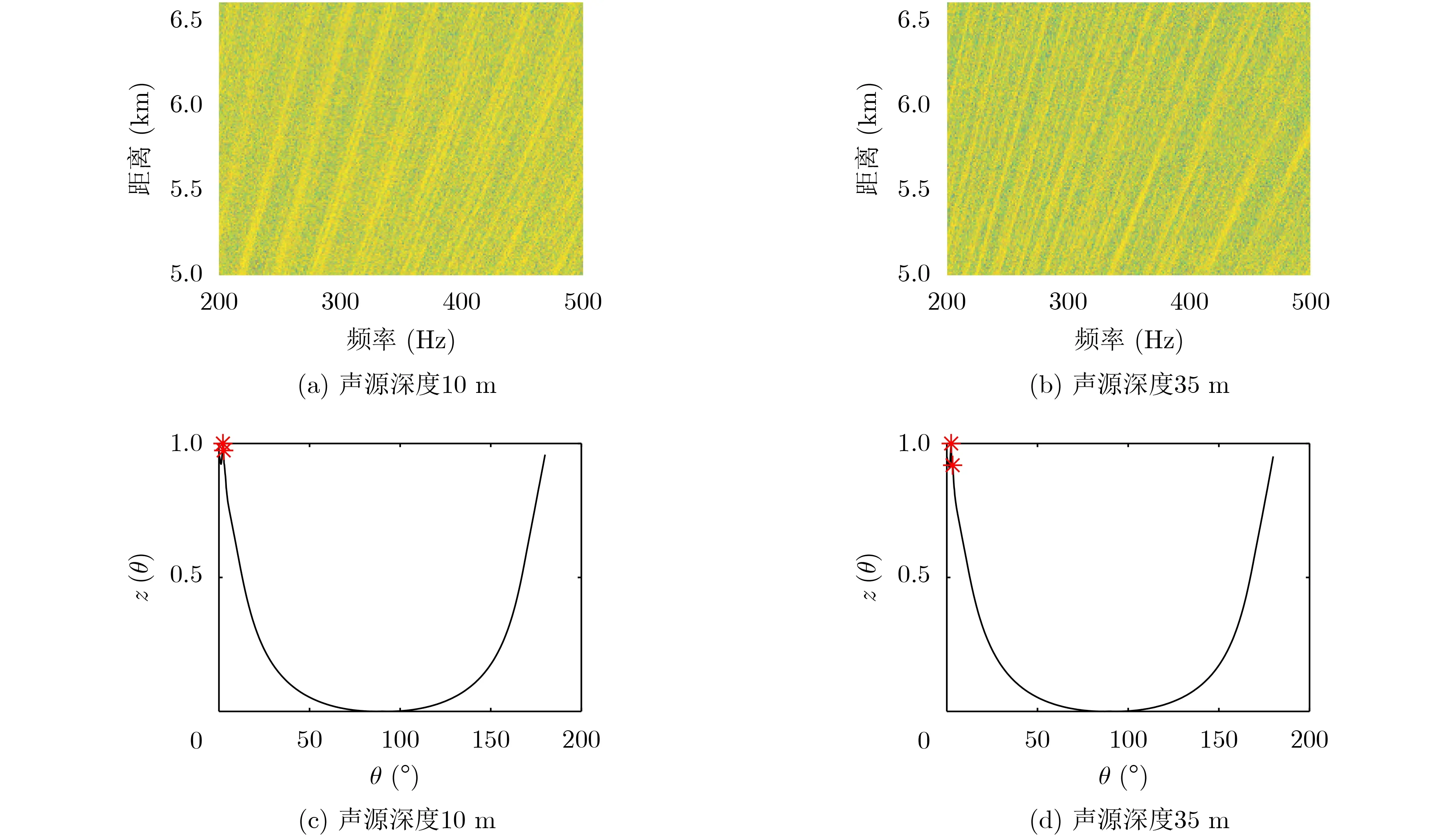
圖8 信噪比為0 dB時輻射噪聲干涉條紋圖像及列方差向量曲線

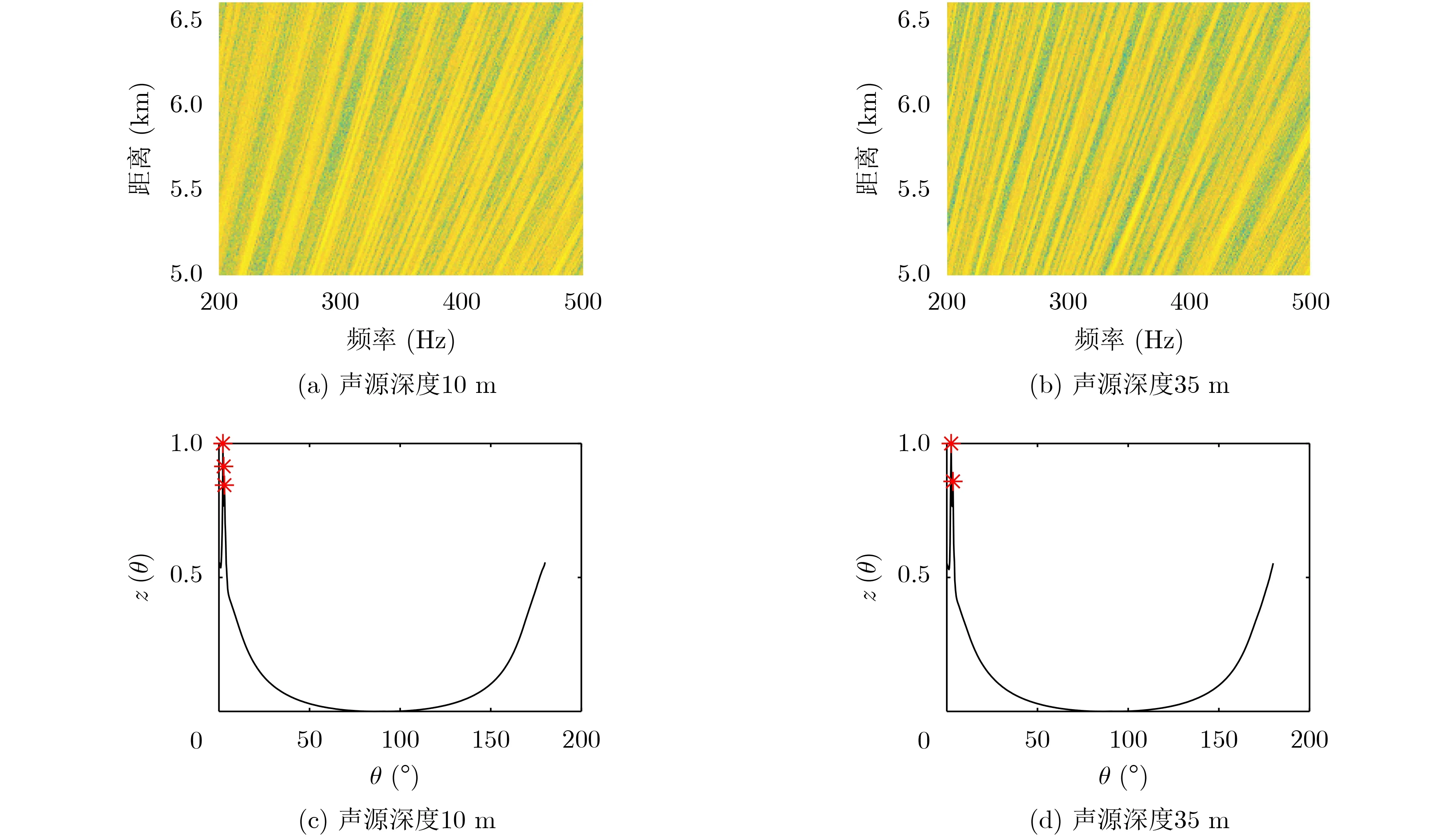
圖9 信噪比為5 dB時輻射噪聲干涉條紋圖像及列方差向量曲線

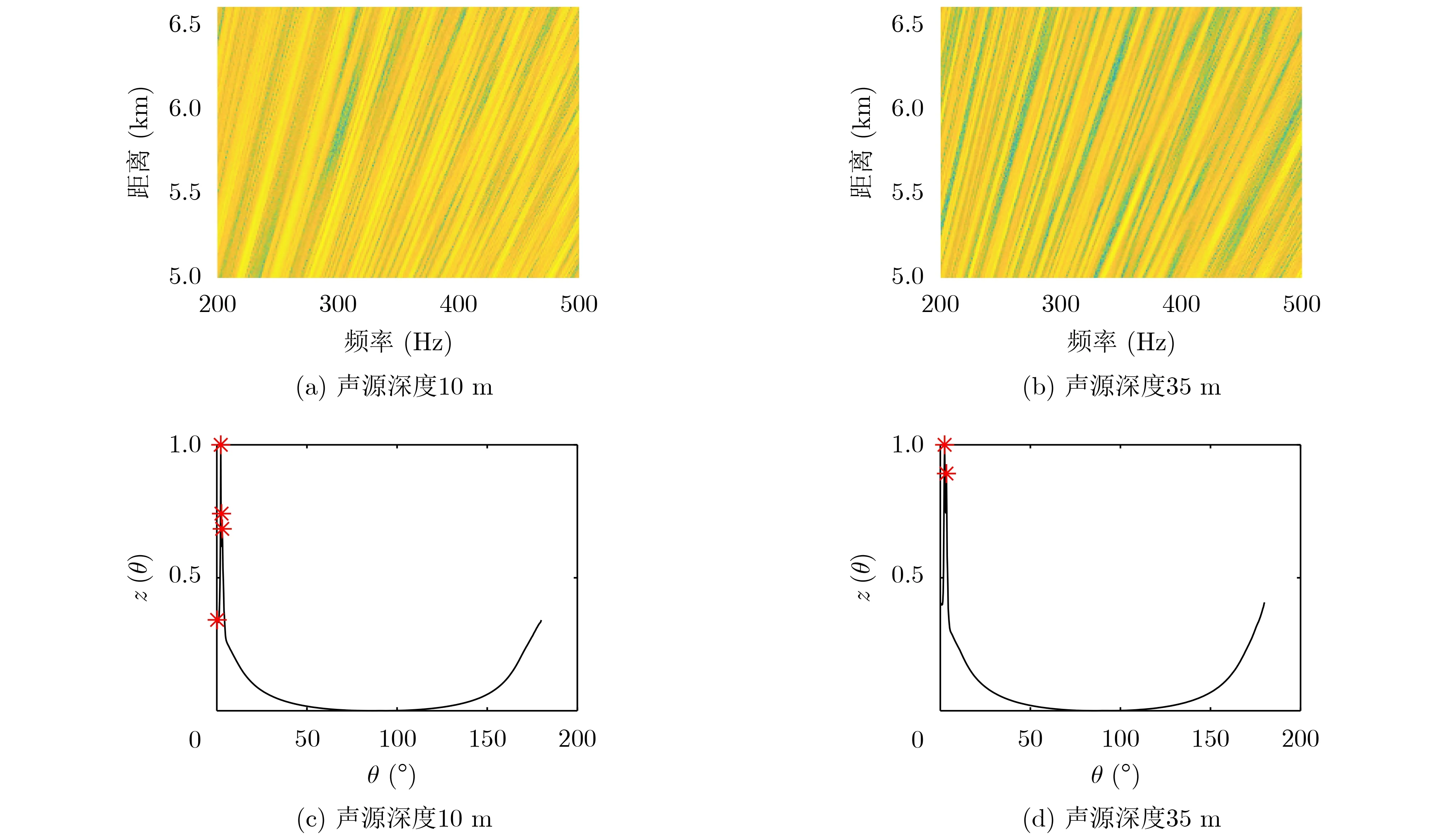
圖10 信噪比為10 dB時輻射噪聲干涉條紋圖像及列方差向量曲線

以上分析可得水面水下目標判決的依據為：在分辨聲源深度時，若目標的干涉條紋Radon變換矩陣的列方差向量峰值個數大于等于門限值時，判定聲源為水面目標；若目標的干涉條紋Radon變換矩陣的列方差向量峰值個數小于門限值，判定聲源為水下目標。根據前文的分析，在典型負躍層淺海環境中，門限值選取為3。

3 深度判別性能仿真分析

仍采用圖1所示環境參數進行分析，選取信號頻率范圍200～500 Hz，頻率分辨率1 Hz，距離范圍5.0～6.6 km，距離采樣間隔1 m，接收器深度選取13 m, 30 m, 35 m, 40 m和45 m，根據式(12)計算干涉條紋Radon變換矩陣的列方差向量并得到其峰值個數，仿真在這些接收器深度下的不同深度目標的分辨結果。定義深度15 m以上的聲源為水面目標，深度為15 m及以下的聲源為水下目標。圖11給出了深度為5～80 m、深度間隔為1 m共76個不同深度的目標在5種不同深度的接收器下列方差向量的峰值個數，共380個仿真結果，其中縱坐標表示列方差向量的峰值個數為特定值時的水面或水下目標個數占水面或水下目標總數的比例。通過圖11可知，水面目標的峰值個數較大，主要分布在3～4區間；水下目標的峰值個數較小，主要分布在1～2區間。方法具有一定可分性。

設定水面水下目標分辨門限值為3，得到5個不同深度接收器對不同深度聲源的深度判別結果，若深度判別結果中判定為水面目標的接收器個數大于2個，認定目標為水面目標；反之，認定目標為水下目標，最終辨別結果如表2所示。

為了分析接收陣深度分布對方法性能的影響，現在與圖12相同的水文環境下仿真不同接收深度覆蓋范圍的情況。圖12給出了深度為5～80 m、深度間隔為1 m的76個目標在5個不同深度的接收器下，干涉條紋Radon變換矩陣的列方差向量峰值個數的總體分布，選取信號頻率范圍200～500 Hz，頻率分辨率1 Hz，距離范圍為5.0～6.6 km，距離采樣間隔為1 m，橫縱坐標的含義與圖11相同，共760個仿真結果。圖12(a)的接收深度主要覆蓋范圍在負躍層以上，其深度分別為15 m, 18 m, 20 m,22 m和25 m；圖12(b)的接收深度主要覆蓋范圍在負躍層以下，其深度分別為30 m, 35 m, 40 m,45 m和50 m。由圖12可得，方法在不同接收陣深度分布下仍能保持對水面、水下目標的分辨能力，但分辨能力在接收深度無法覆蓋整體水層時下降。設定水面水下目標分辨門限值為3，最終目標辨別結果見表3和表4，計算方法與表2相同。

表2 目標深度分辨結果

表3 接收深度覆蓋范圍為負躍層以上的目標深度分辨結果

表4 接收深度覆蓋范圍為負躍層以下的目標深度分辨結果

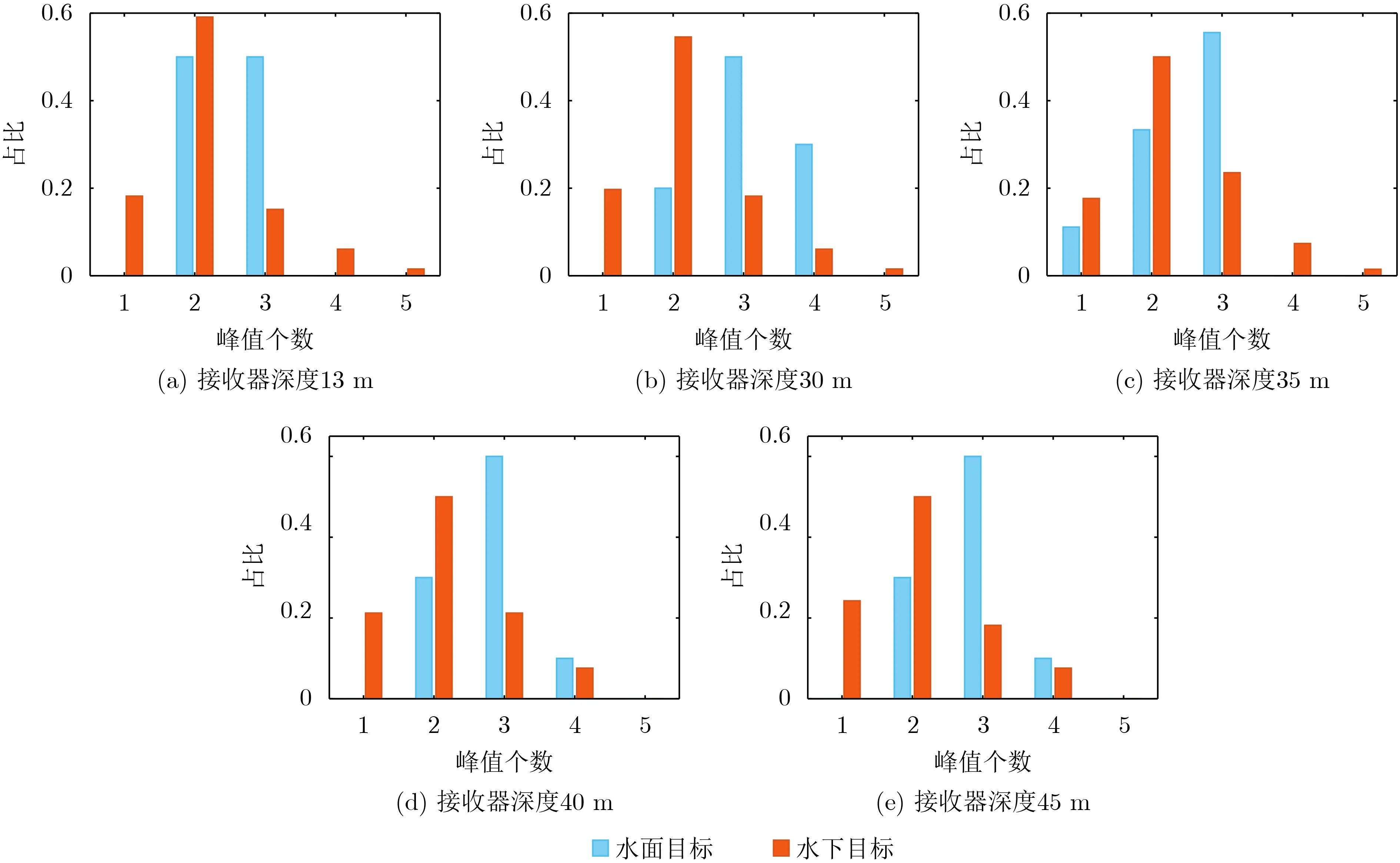
圖11 不同接收器深度的峰值個數計數結果

圖12 不同接收深度覆蓋范圍的峰值個數分布

為了驗證方法對目標距離、信號頻帶的敏感性，現在與圖11相同的水文環境下仿真不同頻率范圍和距離范圍的情況。圖13給出了深度為5～80 m、深度間隔為1 m的76個目標在5個不同深度的接收器下，干涉條紋Radon變換矩陣的列方差向量峰值個數的總體分布，信號的頻率分辨率為1 Hz，橫縱坐標的含義與圖9相同，共760個仿真結果。圖13(a)的信號頻率為100～400 Hz，距離范圍為5～6.6 km，接收器深度分別為13 m, 18 m, 25 m,40 m和50 m；圖13(b)的信號頻率范圍為200～500 Hz，距離范圍為9～10.6 km，接收器深度分別為13 m, 20 m, 30 m, 40 m和45 m。由圖13可得，方法在不同頻率、距離范圍內仍能保持對水面、水下目標的分辨能力。設定水面水下目標分辨門限值為3，最終目標辨別結果如表5和表6所示，計算方法與表2相同。

表5 100～400 Hz頻帶范圍的目標深度分辨結果

表6 9.0～10.6 km距離范圍的目標深度分辨結果

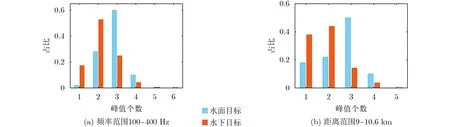
圖13 不同頻帶、距離范圍的峰值個數分布

仿真分析結果可知：在未知海洋聲學環境參數的先驗信息和聲源距離時，方法對于水面水下目標有一定可分性，對目標距離、信號頻帶敏感性低，利用多個深度水聽器進行綜合判決且接收陣深度能覆蓋整體水層的情況下準確率較高，有一定實用意義。

4 海試數據深度判別性能分析

利用2017年3月南海拖曳線列陣的試驗數據對方法進行了驗證，聲速剖面如圖14所示。試驗海域水深為105 m，聲源深度為20 m和8 m，數據處理的頻率范圍為200～300 Hz。在利用功率譜分析得到干涉條紋圖像后，對圖像進行低通濾波，并利用Radon變換檢測濾波后的干涉條紋，最后計算干涉條紋圖像Radon變換矩陣的列方差向量并判斷其峰值個數，信號的具體處理流程見圖15。

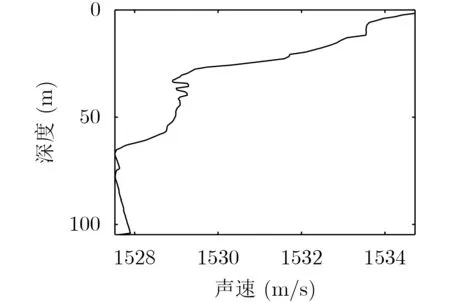
圖14 南海聲速剖面

選取不同聲源深度、不同時間接收的4段輻射噪聲信號，按圖15所示流程處理后，得到輻射噪聲信號的干涉條紋圖像以及Radon變換矩陣的列方差向量，如圖16和圖17所示。圖17(a)、圖17(b)中，聲源深度為8 m的兩組信號中所得峰值個數分別為5個和4個，判定為水面目標；圖17(c)、圖17(d)中，聲源深度為20 m的兩組信號中所得峰值個數均為2個，判定為水下目標，與實際情況相符。與簡正波分解、波導不變量、匹配場處理等傳統被動定位方法相比，本文方法雖不能提供準確的聲源深度估計值，但在存在負躍層的淺海波導條件下，可給出聲源深度的二元判決，對目標類型的判別具有重要的支撐作用。該方法對聲源距離和海洋環境聲學參數等先驗信息的依賴程度低，且無需求解簡正波方差，計算量小，易于實現。

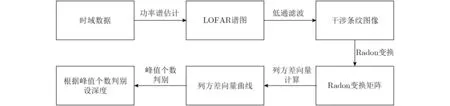
圖15 深度判別處理流程圖

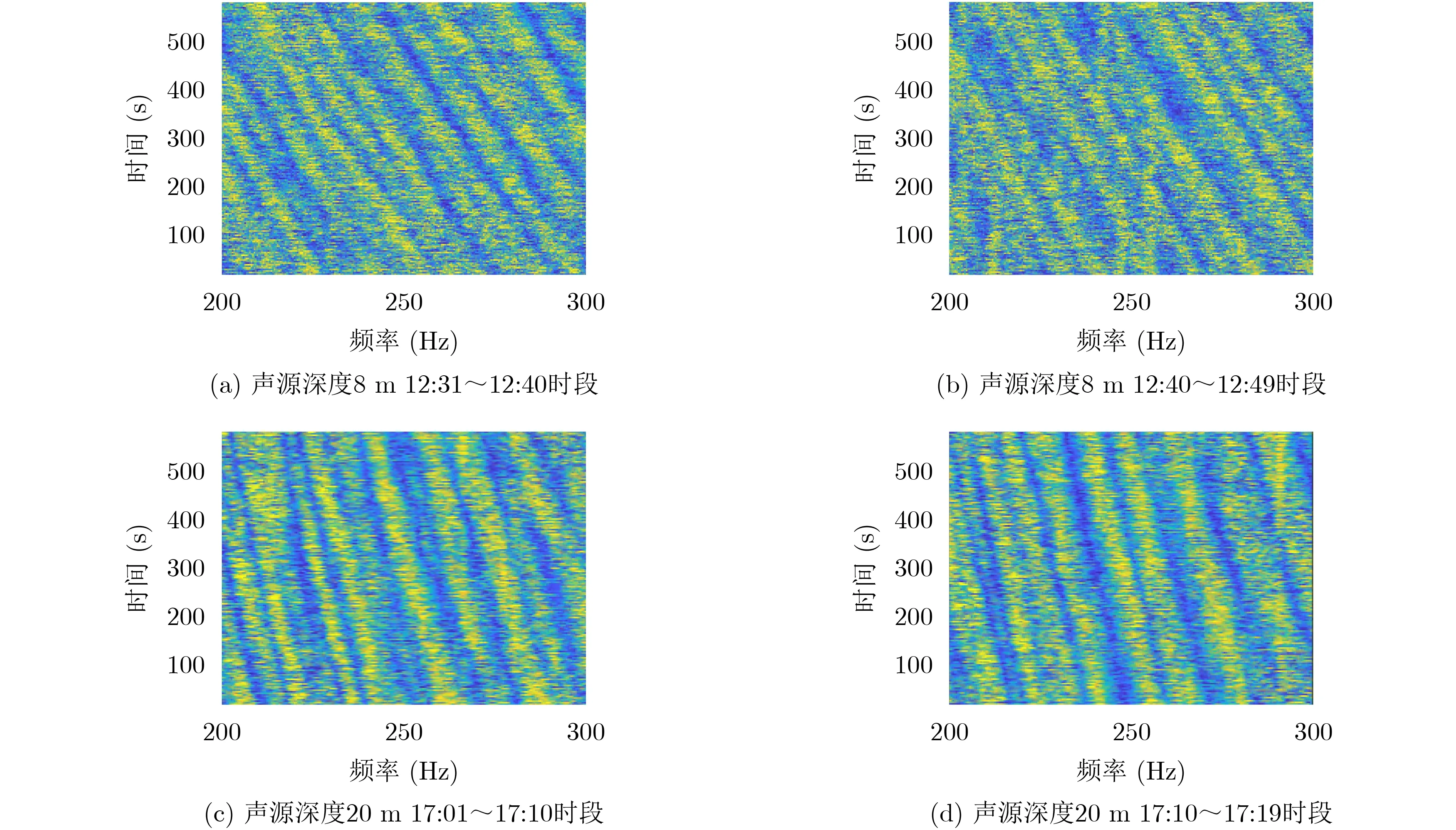
圖16 實際數據的干涉條紋圖像

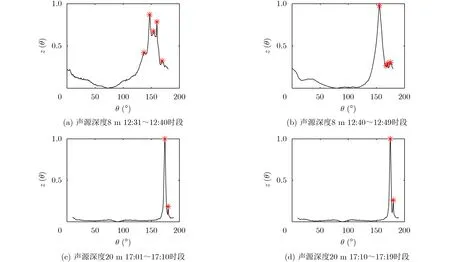
圖17 實際數據的列方差向量曲線

5 結束語

輻射噪聲干涉條紋的分布情況與水聲環境和聲源深度有較強相關關系。在夏季負躍層存在的水文環境中，水面聲源激發的信號中高階簡正波占主導，水下聲源激發的信號中低階簡正波占主導，這種差異性帶來條紋斜率分布的差異性，可以根據干涉條紋斜率分布情況估計聲源的深度區間。本文利用Radon變換對聲場干涉條紋進行處理，得到以峰值個數為表征的干涉條紋斜率分布情況量化指標，進而分辨聲源深度區間。海試數據處理結果表明，水面聲源干涉條紋Radon變換后列方差向量的峰值個數較多，而水下聲源干涉條紋Radon變換后列方差向量的峰值個數較少。相比于傳統的匹配場、匹配簡正波處理以及波導不變量方法，該方法不依賴聲源距離和聲速剖面的先驗信息，既適用于陣列處理后的目標波束信號，也可用于單水聽器接收信號，為水下目標分辨提供新思路。