立足基礎求創新　關注本質重發展

錢小強　錢德春

【摘 要】數學壓軸題的命制要立意先行，聚焦目標的指向性;源于教材，著眼問題的發展性;立足基礎，注重試題的創新性;關注本質，追求試題的關聯性;簡約精致，彰顯試題的人文性.

【關鍵詞】命題立意;立足基礎;關注本質;簡約精致;注重發展

筆者有幸參加了所在地區2021年秋季學期期末八年級數學試卷的命制工作.試卷的壓軸題從教材一道經典問題出發，通過精心設計、反復推敲、細心打磨，最終呈現的試題既考查學生的基礎知識與基本技能，也考查學生的探究意識與創新能力.問題所蘊涵的“變與不變”“數形結合”等思想方法引領學生關注數學本質，尋求問題解決的一般規律與方法，有利于發展學生的數學思維能力.試題簡約精煉，體現了對學生的人文關懷.本文基于試題命制與打磨過程的闡述，談談“立足基礎求創新、關注本質重發展”的初中數學命題思考.1 真題及簡答

如圖1，在平面直角坐標系xOy中，點A，B的坐標分別為（-4，0）、（0，3），連接AB，點P是線段AB上的一個動點（與點A，B不重合），過點P作PC⊥x軸，垂足為C，將線段BC繞點B逆時針旋轉至BD，使∠CBD=∠ABO.連接OD，設點P的橫坐標為m.圖1備用圖

（1）求直線AB的函數表達式;

（2）當m為何值時，△BPC≌△BOD;

（3）在點P運動的過程中，

①在y軸上是否存在一點E，使得∠BED的大小始終不發生變化？若存在，請求出點E的坐標;若不存在，請說明理由;

②直接寫出OD長度的取值范圍.

本題取材于教材原題，以平面直角坐標系為載體，通過對圖形運動中的變與不變規律的探究，考查了全等三角形、勾股定理、直角坐標系及一次函數等知識靈活運用能力、分析問題與解決問題能力，以及對“數形結合”“變中不變”等數學思想方法的感悟.簡答如下：

（1）y=34x+3.

（2）當m=-125時，△BPC≌△BOD.

理由：當m=-125時，yP=65，所以AC=85，CP=65，由勾股定理得：AP=2，AB=5，所以BP=AB-AP=3，所以BO=BP，因為∠CBD=∠ABO，所以∠PBC=∠OBD，從而有△BPC≌△BOD.

（3）①存在.如圖2，在y軸上取點E（0，-2），連接DE.易證△EBD≌△ABC，所以∠BED=∠BAC，由于∠BAC的大小不變，所以∠BED的大小也不變.

②因為點P運動的過程中，∠BED大小始終不變，所以點D在射線ED上運動.

當點P與點A重合時，點C與點A重合，點D與點E重合，此時D（0，-2），OD=2;圖2 圖3

當點P與點B重合時（如圖3），點C與點O重合，此時點D運動至點D1處，過點D1作D1H⊥OB，易得△BAC≌△BED1，所以∠BD1E=∠BCA=90°，D1E=CA=4，求得D1H=125，從而BH=95，OH=65，進而OD1=655>2.

當OD⊥ED1時，OD的長度最小，因為BO=BD1，易證∠OD1H=∠OD1D，所以OD=OH=65.點D從點E運動至點D1的過程中，OD的長度先變小后變大，所以65≤OD<655.2 命題歷程

2.1 命題立意

由于考查內容為蘇科版八年級上冊的全等三角形、軸對稱圖形、勾股定理、直角坐標系及一次函數，故將命題立意確定為：從教材經典問題出發，以平面直角坐標系為背景，考查相關基礎知識、基本方法的靈活運用以及通過幾何推理與代數運算解決問題的能力，體現“數形結合”與“變中不變”等數學思想方法.

2.2 問題原型

（蘇科版八年級上冊第67頁“2.5等腰三角形的軸對稱性”習題第10題）已知：如圖4，△ABC和△CDE都是等邊三角形，且點A，C，E在一條直線上.AD與BE相等嗎？證明你的結論.

這是一道經典問題，由已知條件易得∠ACD=∠BCE，從而證得△ACD≌△BCE，得AD=BE.問題解決運用了等邊三角形性質、全等三角形判定等知識與方法.從圖形變換的角度看，全等的兩個三角形可看作是繞點C旋轉60°而得.

那么筆者思考：能否從該問題出發，通過改變圖形結構、添加問題背景及設置附加條件，命制既考查相關章節的核心知識，又能滲透數學思想方法，還能反映數學本質的數學問題呢？

2.3 試題命制

明確了命題立意、找到了命題素材，接下來就是試題命制層面的工作.試題命制經歷了“化靜為動、數形結合，明晰主次、以動帶動，適當鋪墊、合理優化，刪繁就簡、簡中求道”的不斷取舍與整合、優化與完善的過程.

2.3.1 化靜為動，數形結合

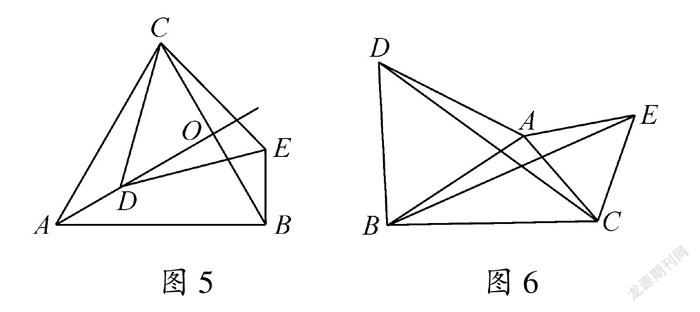
教材問題中的兩個等邊三角形的公共頂點C與另兩個頂點A，E在同一直線上.當點A，C，E不在一條直線上時，如圖5，根據“SAS”仍有△ACD≌△BCE，故AD=BE、∠CAD=∠CBE仍然成立.事實上，人教版八年級上冊“第十三章軸對稱”復習題第12題：“如圖6，△ABD，△AEC都是等腰三角形.求證BE=DC.”正是研究的三點不共線情形.圖5無論點D怎么變化，若∠CAD大小不變，∠CBE的大小也不變，若點D沿著射線AD運動時亦如此.基于這樣的思考，將圖形中的元素動起來，再尋求變化中的不變，便于利用直角坐標系與直角三角形線段關系代數化解決.要保證∠CAD大小不變，令AD⊥BC，將圖形位置特殊化.于是，試題初稿出籠. 圖7

一稿 如圖7，在平面直角坐標系xOy中，△ABC和△CDE都是等邊三角形，AC=4，點B，C在y軸上，點D為x軸上點A右側的一個動點.

（1）試探索：在點D運動的過程中，∠CBE的大小發生變化嗎？請說明理由;

（2）連接OE，求OE長度的最小值.

這里的問題（1）是問題（2）的鋪墊，由前面的分析可知：無論點D如何運動，由于∠CBE=∠CAD，而∠CAD=30°保持不變，所以∠CBE也不變.事實上，由等邊三角形ABC易得∠CAO=30°，故點E在y軸右側且與射線BO所夾的角為30°的射線上運動.由“點到直線垂線段最短”知：在點E的運動過程中，點A，C，O等定點到動點E的距離均存在最小值.這里選擇最特殊也是最簡單的原點O進行探究.顯然，當OE⊥BE時，OE長度最小.

2.3.2 明晰主次，以動帶動

直角坐標系的作用在于通過坐標與線段長度的相互轉化，將圖形問題代數化或將數量關系圖形化，從而有利于問題解決.但觀察“一稿”發現：直角坐標系對問題解決沒有發揮作用，有“為坐標系而坐標系”之嫌.若再給出圖形中某些運動的元素，從而導致其他元素隨之運動，這種主變量與因變量關系可以讓直角坐標系成為理想的探究工具.

由于在AC上一定存在點P，使得△CPD≌△COE，此時PD⊥x軸（或PD∥y軸）.若添加該條件，則由線段AC，OC確定從而點P的位置也唯一確定，只要滿足CP=CO即可，可這樣的話問題的探究價值就打了折扣.遂改變思路：保持PD⊥x軸不變，將點P設為主動點，由點P在AC上運動導致點D在AO上運動，這時點D成了從動點，再給出等邊三角形CDE的條件.為引導問題代數化思考，條件中給出動點P的橫坐標為m.這既使圖形“動”了起來，讓直角坐標系有了用武之地，又減少了問題的干擾元素、增加了問題的思維含量.這種變化具有生成性，更加順暢自然.至此二稿形成.

二稿 如圖8，在平面直角坐標系xOy中，△ABC是等邊三角形，點A在x軸上，點B，C在y軸上，AC=4，點P為線段AC上一個動點（與點A、C不重合），橫坐標為m.過點P作PD⊥x軸，垂足為D，以線段CD為邊向右下方作等邊△CDE，連接OE，BE.

（1）當m為何值時，△CPD≌△COE;

（2）在點P運動的過程中，

①∠CBE的大小是否發生變化？若不變，請求出∠CBE的度數;若變化，請說明理由;

②若點E剛好落在x軸上，求此時m的值;

（3）求OE長度的最小值.

2.3.3 適當鋪墊，合理優化

深入思考后發現：二稿的問題（1）中△CPD≌△COE的條件是CP=CO=2，此時點P恰為AC中點，過于特殊化，沒有體現“任意與變化”的意圖，使幾何推理與代數運算的命題立意落空，故從3個方面進一步優化.

優化一：變特殊圖形為一般圖形.將兩個等邊三角形改為兩個頂角相等的等腰三角形，其中AC=5，OC=3.這樣，要求出m值必須先用m的代數式表示PD的長，進而轉化為求點P的縱坐標.

優化二：在“求點P的橫、縱坐標關系”上思考.這種關系可由三角形相似得到，也可根據一次函數關系求得.但由于八年級學生沒有研究相似圖形，故設置“求AC所在直線的函數表達式”的問題，一方面便于點P的縱坐標的表示，為后續問題的解決搭建腳手架;另一方面符合考查“一次函數”知識的內容目標.

優化三：將重復問題適當合并.由于問題（2）②與問題（3）都屬于點E在運動過程中的兩個特殊位置，故將兩個問題合并為“求OE長度的取值范圍”這樣一個問題.

通過優化，“三稿”呼之即出.

三稿 如圖9，在平面直角坐標系xOy中，△ABC是等腰三角形，AC=BC，點A在x軸上，點B，C在y軸上，A（-4，0）、C（0，3），點P為線段AC上一動點（與點A、C不重合），過點P作PD⊥x軸，垂足為D，以線段CD為邊向右下方作等腰△CDE，且滿足∠DCE=∠ACB，CD=CE，連接OE、BE，設點P的橫坐標為m.

（1）求經過點A，C的直線的函數表達式;

（2）當m為何值時，△CPD≌△COE;

（3）點P在運動的過程中，

①∠CBE的大小是否發生變化？請說明理由;

②求OE長度的取值范圍.

2.3.4 刪繁就簡，簡中求道

反復研究發現，三稿中仍有4處值得推敲：一是圖形無效線段多，解決問題時用到的∠DCE=∠ACB、CA=CB、CD=CE與線段AB，DE無關;二是直接呈現點B的坐標導致問題（3）①思維含量降低，沒有達到壓軸題的預期難度;三是條件的語言不夠精煉.如“△ABC是等腰三角形”與“AC=BC”重復，“點A在x軸上，點C在y軸上”與“A（-4，0）、C（0，3）”重復;四是“求OE長度的取值范圍”過程復雜，可以通過“幾何直觀”加“適當運算”得到，不必讓學生因書寫而花費太多時間.綜合以上因素，最終決定刪繁就簡：一是精簡圖形結構.去掉圖9中的線段AB，DE，BE，讓圖形變得簡潔;二是精細呈現方式.將問題（3）①改為讓學生探究圖9中點B的存在性，在圖形運動中探究不變關系;三是精煉數學語言.將“△ABC是等腰三角形，AC=BC，點A在x軸上，點B、C在y軸上，A（-4，0）、C（0，3）”這段文字壓縮為“點A、C的坐標分別為（-4，0）、（0，3），連接AC”;四是精減解答要求.將“求OE長度的取值范圍”精減為“直接寫出OE長度的取值范圍”，并適當調整圖形的字母，最終形成第四稿（見真題）.

顯然，第四稿刪除了雜亂且與考查內容無關的信息和繁瑣的解題過程要求，圖形結構更簡潔、語言表達更簡約、問題設置更合理、解題過程更順暢.3 命題感悟

試題命制的曲折過程讓筆者充分感受到命題的艱辛與困苦，也享受命題成功的愉悅與愜意，同時還深切感悟到：數學壓軸題的命制要立意先行，聚焦目標的指向性;源于教材，著眼問題的發展性;立足基礎，注重試題的創新性;關注本質，追求試題的關聯性;簡約精致，彰顯試題的人文性.

3.1 立意先行，聚焦目標的指向性

試題的命制經常經歷“立意—形散—神聚”的過程.命題立意是試題之魂，決定了試題的意境與層次.該試題在命制之初就明確了命題立意.從考查目標上說，就是立足基礎、著眼發展、關注能力、指向素養，如考查數學探究的能力與思想方法的感悟;從命題方式上說，就是源于教材、有效關聯、力求創新、適當綜合，如考查三角形全等與相似、直角三角形相關性質、直角坐標系的綜合與聯系.

3.2 源于教材，著眼問題的發展性

許多優秀試題都源自于教材.教材與試題的依據都是課程標準，二者可謂“同源同宗”.數學命題要“重視教材例習題的的作用，引導學生回歸課本和知識本源，從數學教材中探‘源’——問題的源頭與原型，充分挖掘教材例題的價值;從數學本質上尋‘宗’——揭示問題與教材、問題與問題之間的內在聯系”[2].如果善于從教材中尋找命題靈感，通過改變問題背景、改變條件或結論、變換設問方式，關聯其他問題等手段，就能命制出“神形兼備”與“神形皆變”的試題.另外，一道好的試題不僅應該有試場效應，還應該具有深遠的發展價值、有繼續研究與思考的空間.

該題就是從課本習題入手，通過改變圖形的位置，增加平面直角坐標系的背景，并將靜態問題動態化處理，利用運動變化中不變的圖形關系設計層次分明的問題，既考查學生對三角形全等、勾股定理和一次函數等基礎知識的掌握，也考查了學生動態探究的能力以及對“數形結合”“變中不變”等數學思想方法的感悟.

從發展角度來看，一是利用教材問題的發展性.教材中的例習題及相關素材都是精心選擇與設計的，既是教材的資源與母體，也是命題的素材與原型，深入研究教材的編寫意圖，挖掘教材資源的內涵，可以讓教材在教學與命題中走得更遠.以教材這道題為例，通過命題者的精心設計，發展成了一道試卷的壓軸題.二是試題本身也具有發展性.最終呈現在試卷上的試題只是諸多設想中的一部分.例如：本題還可以求探索以下問題：（1）動點D到點A，B距離之和的最小值;（2）是否存在點P，使點C，P，B，D在同一圓上……

所以，深入研究并利用教材資源的發展性編制試題，是提升試題命制能力的靈丹妙藥.

3.3 立足基礎，注重試題的創新性

作為學習評價的重要載體與依據，數學命題要在“立足基礎”與“適度創新”之間平衡.一方面，要立足基礎，拒絕怪題、偏題，引導教師重視數學的基礎知識、基本技能、基本思想、基本活動經驗的教學，避免陷入題海戰，減輕學生過重的作業負擔.另一方面，要適度創新，激發學生探究欲望，促進學生在掌握通性解法的基礎上發展創新思維、強化創新意識，防止走進機械模仿和套路化的“死胡同”.

該題體現了立足基礎與適度創新有機結合的特點.試題立足基礎，將全等三角形的性質與判定、勾股定理、直角坐標系、一次函數等基礎知識融于一題，體現了對方程與代數化、坐標與長度的相互轉化等基本方法的考查.同時試題又有所創新.如第（3）問“在y軸上是否存在一點E，使得∠BED的大小始終不發生變化？”這種對存在性問題設問方式新穎獨特，激發了學生的探究欲望，是試題的創新所在、活力所在、精彩所在.

3.4 關注本質，追求試題的關聯性

數學教學與命題“要推動學生的學習認知從感性走向知性和理性，即從表面的模糊的認識走向事物聯系和事物本質的把握和判斷，從外部的操作感知走向內部的理解認知”[1].如果命題是建筑，那么立意只能是“畫在圖紙上的大廈”;如果命題是烹飪，即使有足夠的食材，也不一定變為色香味俱佳的美食.命題還需要實際操作，包括素材選擇、結構謀劃、邏輯推敲、語言組織等.在這個過程中，最重要的是從看似雜亂無章、紛繁雜亂的問題中尋找靈感，發現相互間的內在聯系，從而抓住問題的本質.命題者要善于挖掘“不相干”信息之間的內涵與聯系，以這種聯系為紐帶將“散亂”的信息加以整合、結構化，從而產生“意外”的驚喜與收獲.

本題經歷了素材選取與變化、問題發展與變式、結構重組與優化的過程：從“雙等邊三角形”的素材選取到“雙等腰三角形”的合理變化;從對運動中某些“特殊位置的數量關系”的探究與思考到對“整個運動過程中動點路徑”的尋找與計算;從“三角形全等存在性”的探索與確認到“角大小不變性”的猜想與驗證，將圖形運動、圖形全等、圖形與坐標等關鍵要素聯系在一起，從而命制出本真而又靈動的試題.

由此可見：對問題內在聯系的洞察、對數學本質的把握、對試題本真的追求是命制高質量試題的關鍵.

3.5 簡約精致，彰顯試題的人文性

“簡約而不簡單”是一種命題能力、一種命題境界，更是一種命題情懷.比如，命題中刪除圖形中不必要的線條，使圖形結構更加簡潔;刪除重復、冗長的文字，使語言表達更精煉，都體現了“簡約精煉”的命題特色.同時，給出的備用圖方便學生對圖形不同位置的探究;最后一問改為直接寫結果，適度降低答題要求，便于學生利用幾何直觀得到結論，避免繁瑣的書寫過程，這些都彰顯了命題者對學生的人文關懷.

參考文獻

[1]羅建宇.從融合到創新：基于GeoGebra的數學深度教學[J].數學通報，2020（02）：23.

[2]錢德春.回歸遷移優化發展——對一道幾何填空題探究歷程的啟示與思考[J].中學數學雜志（初中），2016（02）：41-44.

作者簡介 錢小強（1981—），男，江蘇泰州人，副校長，中學高級教師;市學科帶頭人，獲省初中數學青年教師基本功比賽一等獎、省教學成果二等獎、市初中數學優秀課一等獎，三次參加泰州市中考命題;主要研究初中數學教學與命題.

錢德春（1963—），男，江蘇泰州人，中學高級教師;江蘇省中學數學專業委員會理事，省初中數學名師共同體導師，泰州學院特聘教授，中國人民大學《復印報刊資料·初中數學教與學》編委，《義務教育數學課程標準（2022年版）》教學要求編寫組成員;主要從事初中數學教學、命題與教師專業發展等研究.