聚焦數學閱讀 演繹別樣精彩

戚立輝

(江蘇省興化中學，225700)

《普通高中數學課程標準》指出:“高中數學課程體現社會發展的需求、數學學科的特征和學生的認知規律,發展學生數學學科核心素養．……強調數學與生活以及其他學科的聯系,提升學生應用數學解決實際問題的能力,同時注重數學文化的滲透．”并要求“不斷引導學生感悟數學的科學價值、應用價值、文化價值和審美價值．”這使得高考數學試題由單純地對數學文化的考查演變為對在各種情境下數學閱讀的考查.本文結合幾道高考試題,對此進行思考．

一、數學閱讀與建筑情境相結合

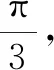
(1)求四棱錐的總曲率;

(2)若多面體滿足:頂點數-棱數+面數=2,證明:這類多面體的總曲率是常數.

解(1)由題可知:四棱錐的總曲率等于四棱錐各頂點的曲率之和.可以從整個多面體的角度考慮,所有頂點相關的面角就是多面體的所有多邊形表面的內角的集合.易知四棱錐共有5個頂點,5個面,其中4個為三角形,1個為四邊形.所以四棱錐的表面內角和由4個為三角形,1個為四邊形組成,則其總曲率為2π×5-(4π+2π)=4π.

(2)設頂點數、棱數、面數分別為n，l，m,所以有n-l+m=2.設第i個面的棱數為xi,所以x1+x2+…+xm=2l.因而總曲率為2πn-π[(x1-2)+(x2-2)+…+(xm-2)]=2πn-π(2l-2m)=2π(n-l+m)=4π.故這類多面體的總曲率是常數.

評注本題考查立體幾何的新定義問題,能夠正確讀懂“曲率”的概念是解決問題的關鍵.同時也讓學生在解決數學問題之余體會現代建筑之美,感悟數學的審美價值.

例2攢尖是古代中國建筑中屋頂的一種結構形式，宋代稱為撮尖,清代稱