考慮摩擦效應的工業純鈦TA2熱壓縮變形本構方程及熱加工圖

王曉溪，張翔，董興兵，劉穎，唐虓，徐巖

考慮摩擦效應的工業純鈦TA2熱壓縮變形本構方程及熱加工圖

王曉溪1，張翔2，董興兵1，劉穎1，唐虓1，徐巖1

（1.徐州工程學院 機電工程學院，江蘇 徐州 221018；2.江蘇徐工工程機械研究院有限公司，江蘇 徐州 221004）

研究工業純鈦TA2在變形溫度為800～950 ℃、應變速率為0.001～1 s?1、壓下量為50%條件下的熱壓縮變形行為，構建材料高溫本構方程及熱加工圖。利用Gleeble–3500熱模擬試驗機進行熱壓縮試驗，對實測流變曲線進行摩擦修正，通過線性回歸擬合等方法建立本構方程，基于動態材料模型構建工業純鈦TA2熱加工圖，確定材料最佳熱變形區域。工業純鈦TA2熱變形激活能為473.491 kJ/mol應力指數為3.876 6；最佳熱變形參數為變形溫度850～950 ℃、應變速率0.02～0.35 s?1。工業純鈦TA2摩擦修正后的流變應力值均低于實測值，流動應力隨變形溫度的升高和應變速率的減小而降低。所建立的Arrhenius本構模型可較為準確地描述工業純鈦高溫流變行為。工業純鈦TA2在中高溫中等應變速率條件下加工性能良好，該區域材料發生了動態再結晶組織轉變。

摩擦修正；工業純鈦TA2；熱變形；本構方程；熱加工圖

工業純鈦（commercially pure titannium，CP–Ti）具有比強度高、質量輕、耐熱性好以及耐腐蝕性能優良等突出優點，是重要的結構金屬和生物醫用材料，近年來在航空航天、生物醫學、海洋船舶和石油化工等領域得到了廣泛的應用[1-2]。純鈦為密排六方結構，室溫變形時可開動滑移系較少，制備加工較為困難，屬于難變形材料，因此生產中多采用熱加工的方法實現成形。

材料熱變形行為是一個高溫、動態、瞬時的復雜過程，具有多因素、強耦合、非線性和非穩態等特點[3]。材料的本構方程用于表征熱變形過程中材料流變應力與應變量、變形溫度和應變速率等熱力學參數間的函數關系，可為金屬熱變形工藝設計和數值模擬研究提供理論基礎[4-5]。熱加工圖可以直觀地反映材料在不同條件下的變形機制，并預測材料最佳變形區域，是制定及優化熱加工工藝的重要理論依據[6]。實際熱壓縮變形過程中，試樣兩端面與熱模擬機壓頭之間不可避免地存在著接觸摩擦，這會導致其應力狀態發生改變，產生不均勻變形，甚至會出現嚴重鼓肚，從而使實測流變曲線偏離真實值，給本構方程構建帶來較大計算誤差[7-9]。因此，有必要對原始試驗數據進行摩擦修正，以獲得更為準確的流變曲線。

文中以工業純鈦TA2為研究對象，基于熱壓縮模擬試驗研究其在不同條件下的熱變形行為。在對實測流變曲線進行摩擦修正的基礎上，求解材料常數及變形激活能，構建工業純鈦TA2高溫本構方程，并基于動態材料模型構建熱加工圖，確定材料最佳的熱變形區域，以期為工業純鈦熱變形工藝參數優化提供理論參考。

1 熱壓縮模擬試驗

選用的材料為寶雞某有色金屬公司提供的退火態TA2鈦棒，其主要化學成分如表1所示。

表1 工業純鈦TA2化學成分

Tab.1 Chemical composition of commercially pure titanium TA2 wt.%

試驗在Gleeble 3500熱模擬試驗機上進行，熱壓縮試樣尺寸為10 mm′15 mm。為減小摩擦，試驗前在試樣上下兩端面涂覆高溫潤滑劑并粘貼鉭片。熱壓縮試驗在真空環境下進行，試樣首先以5 ℃/s的升溫速率加熱至指定溫度（800、850、900、950 ℃），并保溫5 min使其受熱均勻，隨后在不同應變速率下（0.001、0.01、0.1、1 s?1）進行單軸壓縮變形，壓下量為50%（對應真應變≈0.7）。變形結束后，對試樣進行水淬以保留高溫組織。利用MDS400型倒置金相顯微鏡觀察工業純鈦TA2熱壓縮變形組織，觀察面為試樣中心縱剖面。

2 流變應力的摩擦修正

圖1為工業純鈦TA2熱壓縮試樣變形前后實物。為消除摩擦效應對流變應力的影響，采用一種簡單有效的方法對熱壓縮過程中材料的流變應力進行摩擦修正[10]，相關計算見式（1）。

式中：D、h分別為熱壓縮變形過程中試樣的瞬時直徑和瞬時高度；Fi為瞬時載荷；m為摩擦因子，與試樣外形尺寸之間存在定量關系。

圖2為摩擦修正前后工業純鈦TA2真應力與真應變關系曲線。由圖2可知，熱壓縮變形過程中，摩擦效應對材料流變應力具有顯著影響，各條件下摩擦修正后的流變應力值均小于實測應力值，且隨著應變量的增加，流變應力實測值與摩擦修正值之間差值逐漸增大。工業純鈦TA2熱壓縮過程受形變、回復、再結晶與相變等多種機制交互作用的影響[11]，變形溫度和應變速率對流變應力的影響十分顯著。初始變形時，流變應力隨應變的增加迅速升高，加工硬化現象十分明顯。當應變增加到一定數值時，材料內部軟化作用占據主導，流變應力增幅逐漸變緩并達到峰值，之后基本保持不變或略微下降，變形進入穩態階段，軟化和硬化之間達到了動態平衡。觀察圖2還可以發現，當應變速率恒定時，流變應力隨溫度的增加而降低；當變形溫度恒定時，流變應力隨應變速率的增加而升高。

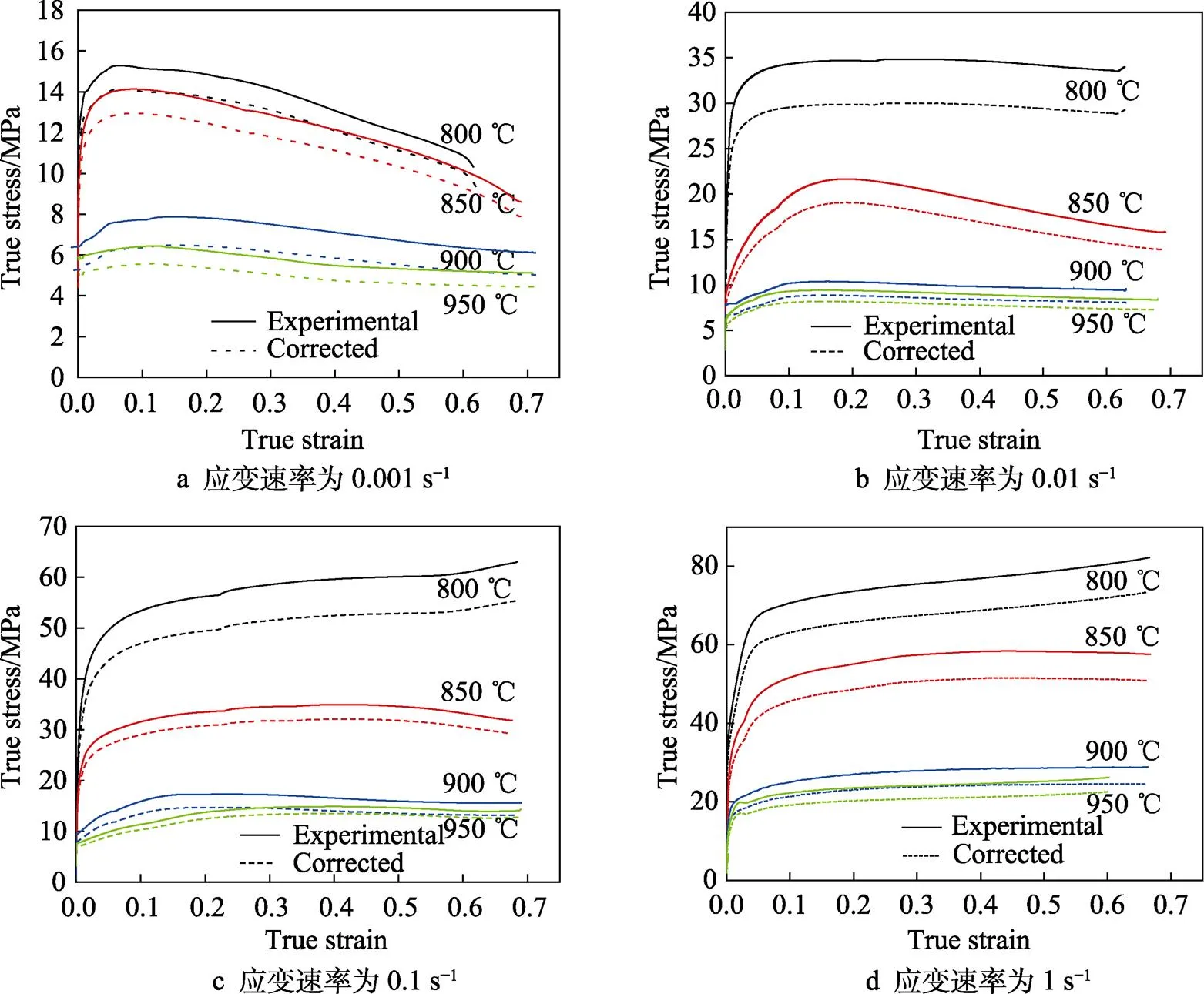
圖2 摩擦修正前后工業純鈦TA2真應力–應變曲線

3 高溫本構方程的建立

金屬高溫變形行為是一個受熱激活控制的過程，受應變量、變形溫度和應變速率等參數的影響。文中基于熱壓縮模擬試驗，建立了變形溫度和應變速率與材料熱變形行為的Arrhenius模型[12-13]，通常采用以下3種形式，分別見式（2）—（4）。

式中：、1、2、、、均為與溫度無關的材料常數，且、、之間滿足=/；為流變應力；為變形激活能；為氣體常數，通常取8.314 J/(mol·K)；為熱力學溫度。其中，式（2）為雙曲正弦函數關系方程，對所有的應力狀態均適用，式（3）為指數函數關系方程，適用于高應力水平（>1.2），式（4）為冪函數關系方程，適用于低應力水平（<0.8）。

當一定時，為常數。對式（3）—（4）兩邊取自然對數，得：

對式（2）兩邊分別取對數，可得：

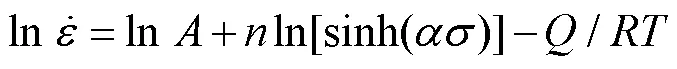
由式（7）可得：

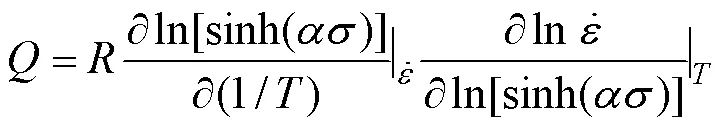
將不同變形溫度下工業純鈦TA2的峰值應力、應變速率以及求得的代入式（7），繪制出各參數間的關系圖，并進行線性回歸，如圖3c和圖4所示。對圖3c和圖4中各直線斜率取平均值，由式（8）計算求得熱變形激活能473.491 kJ/mol。

Zener等[14]提出用溫度補償變形速率因子參數來表示應變速率和變形溫度之間的關系，如式（9）所示。

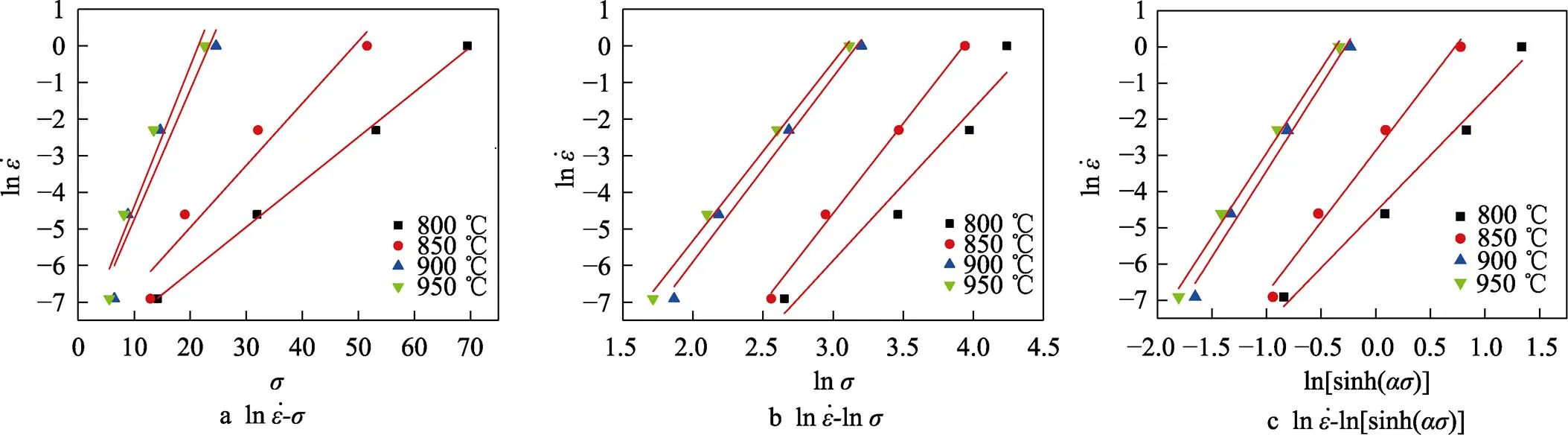
圖3 工業純鈦TA2應變速率與流變應力相關性

圖4 工業純鈦TA2變形溫度與流變應力相關性

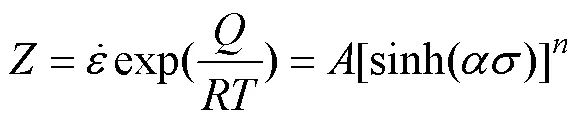
對式（9）兩邊取對數，可得：

將不同變形溫度下工業純鈦TA2熱變形激活能和應變速率值代入式（9），得到不同變形條件下的值。進一步將不同條件下的流變應力代入式（10），通過線性擬合得到如圖5所示的ln–ln[sinh()]關系。計算圖5的直線斜率和截距，求得=3.876 6，=7.970 27′1020。

圖5 工業純鈦TA2的Z參數與流變應力相關性

將上述所求的材料常數和熱變形激活能值代入式（2），求出工業純鈦TA2高溫熱變形本構方程，見式（11）。

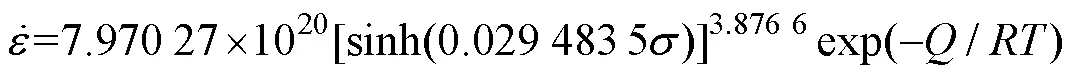
式（11）適用于描述變形溫度為800～950 ℃、應變速率為0.001～1 s?1、壓縮變形量為50%時工業純鈦TA2的流變應力行為。

根據雙曲正弦函數的定義及式（9），可進一步用式（12）表示流變應力[15]。

為驗證文中所建立本構模型的可靠性，由式（9）計算出不同變形溫度和應變速率下的Z參數，代入式（12）求得不同條件下的流變應力預測值，并將其與流變應力修正值（實驗值）進行對比，結果如圖6所示。從圖6可以看出，預測值與實驗值吻合度較高，相關度R和平均絕對相對誤差EAARE分別為0.967 68和4.39%，表明本試驗條件下基于Arrhenius模型所建立的工業純鈦TA2熱變形流變應力本構方程是合理的。

4 工業純鈦TA2熱加工圖

文中基于動態材料模型（dynamic material modeling，DMM）構建工業純鈦TA2熱加工圖。DMM模型[16]將材料的熱變形過程視為一個封閉的能量耗散系統，認為由外界輸入工件的總能量可分為2個部分：一部分為材料因塑性變形所消耗的黏塑性熱量，稱為耗散量；另一部分為材料因微觀組織變化而消耗的能量，稱為耗散協量。

實際熱變形過程，通常采用耗散協量與理想線性耗散能量max的比值來表示功率耗散特性，其計算見式（13）。

式中：為功率耗散因子；為應變速率敏感因子。功率耗散因子值越大，則組織耗散功率越大，但并不表明材料越容易加工和變形，還需要結合失穩判據來判斷分析。

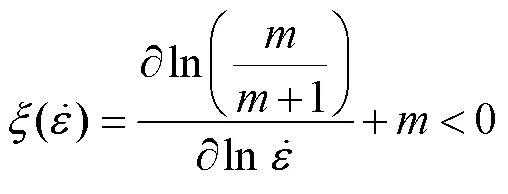
根據式（13）和式（14）可計算出工業純鈦TA2在不同變形條件下的功率耗散因子和失穩因子。在對熱壓縮試驗數據進行3次樣條函數插值的基礎上，繪制出材料的功率耗散圖和失穩圖，并將二者疊加得到工業純鈦TA2熱加工圖，如圖7所示。

對圖7進行分析可知，可將工業純鈦TA2熱加工圖分為4個不同的區域：（1）流變失穩區，該區域被失穩區覆蓋，對應圖7中灰色陰影區域，主要集中在低溫高應變速率范圍（800～850 ℃、0.05～1 s?1），材料功率耗散因子較小，不利于工業純鈦的加工成形，實際生產中應盡量避免；（2）不穩定變形區，該區域對應的工藝條件為低溫低應變速率（800～ 825 ℃、0.001～0.03 s?1），盡管此處功率耗散因子較大，但由于工藝參數范圍較窄，部分等值線靠近流變失穩區，十分不穩定，當變形溫度和應變速率稍微發生變化時，材料便可能發生失穩[18-19]，因此，不能作為工業純鈦TA2的最佳變形區；（3）最佳變形區，該區域功率耗散因子約為0.37，主要對應中高溫中等應變速率變形區（850～950 ℃、0.02～0.35 s?1），結合圖8所示的熱變形組織可知，該條件下材料熱激活作用增強[20]，且具有足夠的時間發生組織轉變，材料流變軟化特征明顯，變形過程中存在明顯的動態再結晶現象（見圖8a），是工業純鈦TA2較為理想的熱變形區域，這一結論也與圖2所示該條件下材料高溫流變曲線變化特征相吻合；（4）其他變形區，該區域為除上述區域外的其他部分，主要對應中高溫低應變速率范圍，該區域材料功率耗散因子較小（<0.32），但未出現明顯的失穩現象（見圖8b）。

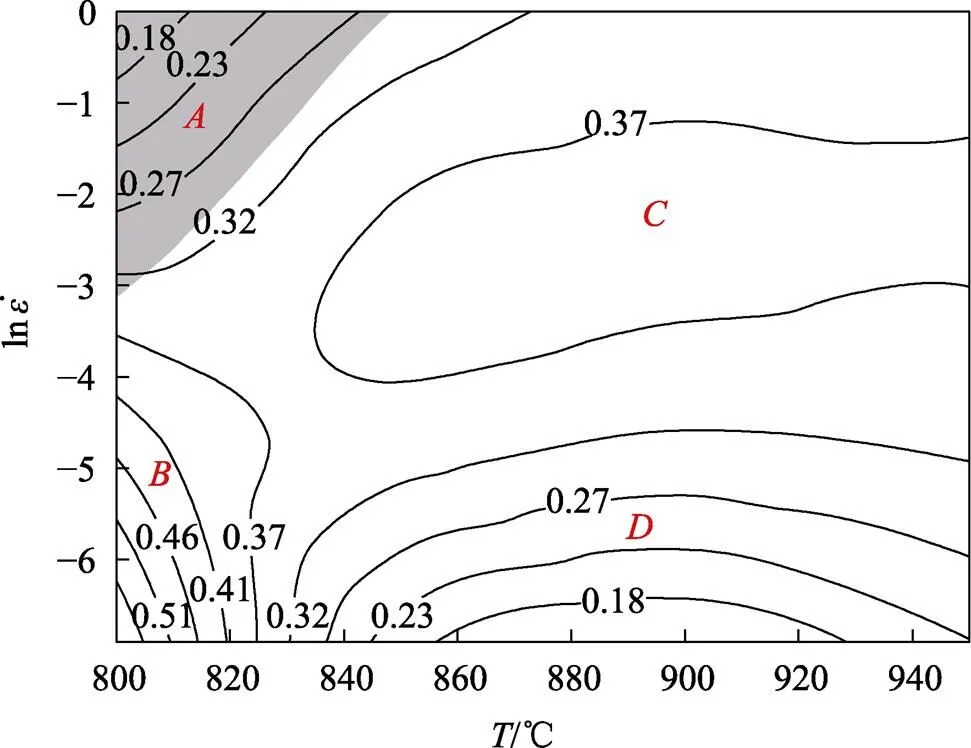
圖7 工業純鈦TA2熱加工圖（e≈0.7）

圖8 不同條件下工業純鈦TA2熱變形組織

5 結論

1）摩擦效應對工業純鈦TA2高溫流變應力具有顯著影響，各條件下摩擦修正后的流變應力值均小于實測值，且隨著應變的增加，兩者之間的差值逐漸增大。當應變速率恒定時，流變應力隨溫度的增加而降低；當變形溫度恒定時，流變應力隨應變速率的增加而升高。

3）工業純鈦TA2最佳熱變形區間為變形溫度850～950 ℃，應變速率0.02～0.35 s?1，該工藝條件下材料發生了動態再結晶組織轉變。

[1] 趙永慶, 葛鵬, 辛社偉. 近五年鈦合金材料研發進展[J]. 中國材料進展, 2020, 39(S1): 527-534.

ZHAO Yong-qing, GE Peng, XIN She-wei. Progresses of R&D on Ti-Alloy Materials in Recent 5 Years[J]. Materials China, 2020, 39(S1): 527-534.

[2] YANG He, FAN Xiao-guang, SUN Zhi-chao, et al. Recent Developments in Plastic Forming Technology of Titanium Alloys[J]. Science China Technological Sciences, 2011, 54(2): 490-501.

[3] MORAKABATI M, HAJARI A. Hot Working Behavior of Near Alpha Titanium Alloy Analyzed by Mechanical Testing and Processing Map[J]. Transaction of Nonferrous Metals Society of China, 2020, 30: 1560-1573.

[4] 李立鴻, 鐘敏, 吳淵, 等. 基于熱壓縮的Cu-15Ni-8Sn合金動態再結晶行為研究[J]. 精密成形工程, 2021, 13(2): 91-95.

LI Li-hong, ZHONG Min, WU Yuan, et al. Dynamic Recrystallization Behavior of Cu-15Ni-8Sn Alloy Based on Hot-Compression Test[J]. Journal of Netshape Forming Engineering, 2021, 13(2): 91-95.

[5] 吳文祥, 韓逸, 鐘皓, 等. 2026鋁合金熱壓縮變形流變應力行為[J]. 中國有色金屬學報, 2009, 19(8): 1403-1408.

WU Wen-xiang, HAN Yi, ZHONG Hao, et al. Flow Stress Behavior of 2026 Aluminium Alloy under Hot Compression Deformation[J]. The Chinese Journal of Nonferrous Metals, 2009, 19(8): 1403-1408.

[6] 李軍, 史慶南, 于輝, 等. 純鈦TA1熱變形行為及加工圖[J]. 鋼鐵釩鈦, 2016, 37(2): 37-43.

LI Jun, SHI Qing-nan, YU Hui, et al. Hot Deformation Behaviors and Processing Map of Pure Titanium TA1[J]. Iron Steel Vanadium Titanium, 2016, 37(2): 37-43.

[7] 王天祥, 魯世強, 王克魯, 等. 考慮摩擦和溫升效應的Ti60合金流變曲線修正[J]. 稀有金屬材料與工程, 2021, 50(2): 537-543.

WANG Tian-xiang, LU Shi-qiang, WANG Ke-lu, et al. Correction of Flow Curve of Ti60 Alloy Considering Effects of Friction and Heating[J]. Rare Metal Materials and Engineering, 2021, 50(2): 537-543.

[8] 段園培, 黃仲佳, 余小魯, 等. 基于摩擦修正的TB6合金流變應力行為研究及本構模型建立[J]. 稀有金屬, 2014, 38(2): 202-209.

DUAN Yuan-pei, HUANG Zhong-jia, YU Xiao-lu, et al. Flow Stress Behavior and Constitutive Model of As-Cast TB6 Titanium Alloy Based on Friction Correction[J]. Chinese Journal of Rare Metals, 2014, 38(2): 202-209.

[9] 王曉溪, 董蔚霞, 何敏. 基于摩擦修正的6061鋁合金熱壓縮變形行為及有限元模擬[J]. 徐州工程學院學報: 自然科學版, 2016, 31(1): 68-76.

WANG Xiao-xi, DONG Wei-xia, HE Min. Hot Deformation Behavior and FEM Simulation of 6061 Aluminum Alloy during Hot Compression Based on Friction Correction[J]. Journal of Xuzhou Institute of Technology: Natural Sciences Edition, 2016, 31(1): 68-76.

[10] EBRAHIMI R, NAJA ZADEH A. A New Method for Evaluation of Friction in Bulk Metal Forming[J]. Journal of Materials Processing Technology, 2004, 152: 136-143.

[11] LI K, YANG P. Interaction Among Deformation, Recrystallization and Phase Transformation of TA2 Pure Titanium during Hot Compression[J]. Transaction of Nonferrous Metals Society of China, 2016, 26: 1863-1870.

[12] 張紅鋼, 何勇, 劉雪峰, 等. Ni-Ti形狀記憶合金熱壓縮變形行為及本構關系[J]. 金屬學報, 2007, 43(9): 930-936.

ZHANG Hong-gang, HE Yong, LIU Xue-feng, et al. Hot Deformation Behavior and Constitutive Relationship of Ni-Ti Shape Memory Alloy during Compression at Elevated Temperatures[J]. Acta Metallurgica Sinica, 2007, 43(9): 930-936.

[13] 蘇娟華, 韓亞瑋, 任風章, 等. 工業純鈦TA1熱壓縮變形行為及本構方程[J]. 材料熱處理學報, 2014, 35(5): 196-200.

SU Juan-hua, HAN Ya-wei, REN Feng-zhang, et al. Hot Temperature Compression Deformation Behavior and Constitutive Equation of TA1 Titanium[J]. Transactions of Materials and Heat Treatment, 2014, 35(5): 196-200.

[14] ZENER C, HOLLOMON J H. Effect of Strain-Rate upon the Plastic Flow of Steel[J]. Journal of Applied Physics, 1944, 15(1): 22-32.

[15] 柴希陽, 高志玉, 潘濤, 等. 工業純鈦TA2熱變形過程的流變行為本構方程[J]. 工程科學學報, 2018, 40(2): 226-232.

CHAI Xi-yang, GAO Zhi-yu, PAN Tao, et al. Constitutive Equation for Flow Behavior of Commercially Pure Titanium TA2 during Hot Deformation[J]. Chinese Journal of Engineering, 2018, 40(2): 226-232.

[16] VENUGOPAL S, VENUGOPAL P, MANNAN S L. Optimization of Cold and Warm Workability of Commercially Pure Titanium Using Dynamic Materials Model (DMM) Instability Maps[J]. Journal of Materials Processing Technology, 2008, 202: 201-215.

[17] PRASAD Y V R K, GEGEL H L, DORAIVELU S M, et al. Modeling of Dynamic Material Behavior in Hot Deformation: Forging of Ti-6242[J]. Metallurgical Transactions A, 1984, 15(10): 1883-1892.

[18] 尚筱迪. 工業純鈦TA2熱壓縮變形行為及微觀組織演變[D]. 西安: 西安建筑科技大學, 2019: 58-59.

SHANG Xiao-di. Hot Deformation Behavior and Microstructure Evolution of TA2[D]. Xi'an: Xi'an University of Architecture and Technology, 2019: 58-59.

[19] LI F, WANG Y, LUO Y, et al. Evaluation on the Hot Workability of As-Extruded TA2 Pure Titanium Using Processing Map[J]. Advances in Mechanical Engineering, 2016, 8(4): 1-8.

[20] 李昌民, 黃亮, 趙明杰, 等. Ti-6Cr-5Mo-5V-4Al合金熱加工性能研究[J]. 精密成形工程, 2022, 14(4): 20-27.

LI Chang-min, HUANG Liang, ZHAO Ming-jie, et al. Hot Workability of Ti-6Cr-5Mo-5V-4Al Alloy[J]. Journal of Netshape Forming Engineering, 2022, 14(4): 20-27.

Investigation on Constitutive Equation and Hot Processing Map of Commercially Pure Titanium TA2 during Hot Compression Deformation Considering the Friction Effect

WANG Xiao-xi1, ZHANG Xiang2, DONG Xing-bing1, LIU Ying1, TANG Xiao1, XU Yan1

(1. School of Mechanical & Electrical Engineering, Xuzhou University of Technology, Jiangsu Xuzhou, 221018, China; 2. Xuzhou Construction Machinery Group Co., Ltd., Jiangsu Xuzhou 221004, China)

Hot compression deformation behavior of commercially pure titanium TA2 under the conditions of the deformation temperature of 800-950 ℃, the strain rate of 0.001-1 s?1and the reduction of 50% was investigated to establish the high temperature constitutive equation and hot processing map of TA2. Hot compression tests of commercially pure titanium TA2 were performed with Gleeble-3500 thermal simulator under different deformation conditions. The friction correction were carried out for measured flow curves, the constitutive equation of TA2 was established by linear regression fitting, and the hot processing map of TA2 was constructed based on the dynamic material model to determine the optimal processing parameters. The results showed that the thermal deformation activation energyof TA2 was 473.491 kJ/mol and the stress indexwas 3.876 6. The optimum thermal deformation parameters were the temperatures of 850-950 ℃ and the strain rate of 0.02-0.35 s?1. The flow stress decreases with increase of the deformation temperature and decrease of the strain rate. The friction-corrected flow stress is less than the measured value under the experimental conditions, and the Arrhenius-type hyperbolic sine equation can be used to more accurately describe the hot deformation behavior of commercially pure titanium at high temperature. The commercially pure titanium TA2 exhibits good workability under the conditions of medium-high temperature and medium strain rate, in which the dynamic recrystallization occurs during the hot deformation process.

friction correction; commercially pure titanium TA2; hot deformation; constitutive equation; hot processing map

10.3969/j.issn.1674-6457.2022.06.010

TG146.2

A

1674-6457(2022)06-0071-07

2021–08–22

國家自然科學基金青年科學基金（51905462）；江蘇省自然科學基金面上項目（BK20201150）；江蘇省高等學校自然科學研究重大項目（21KJA460007）；江蘇省“六大人才高峰”高層次人才選拔培養資助項目（GDZB–127）；江蘇省“333高層次人才工程”培養資助項目（2022–3–12–182）

王曉溪（1985—），女，博士，副教授，主要研究方向為輕質金屬材料先進塑性成形工藝及組織性能調控技術。

責任編輯：蔣紅晨