基于超參數優化和雙重注意力機制的超短期風電功率預測

康田雨，覃智君

(廣西大學電氣工程學院，南寧530004)

0 引言

可再生能源發電是當代能源革命的重要組成部分，在近十年間獲得了國際社會的廣泛關注。風力發電作為其中最具代表性的發電方式，因其清潔、易獲取、分布廣等優點獲得了迅猛發展[1 - 2]。但由于風能的強波動性、強間歇性和弱周期性的特點，風電并網給電力系統的安全穩定運行帶來了嚴峻的考驗。超短期風電功率預測精度的提高對于電網制訂合理的經濟調度和機組組合計劃起著至關重要的作用，也有助于減少系統棄風量，提高經濟性。所以，提升風電功率預測準確度對確保電力系統運行的安全性、穩定性和經濟性具有重大意義[3]。

國內外對于風電功率預測問題的研究方法可以分為基于物理建模的方法和基于數據統計的方法兩類[4 - 11]。前者不需要歷史數據，以風電場地形、地表粗糙度、氣象條件和風機分布位置等為基礎信息, 通過求解流體力學、熱力學高維方程組進行功率預測[4 - 6]。該類方法建模復雜、求解難度高、計算量大，一般多應用于新建風場[7 - 9]。后者利用歷史功率和天氣數據樣本挖掘潛在規律，建立歷史數據和預測目標間的映射關系，應用較為廣泛。數據統計方法可細分為傳統統計方法和基于數據驅動的機器學習算法。近年來，人工神經網絡(artificial neural network，ANN)、支持向量機(support vector machine，SVM)、極限學習機(extreme learning machine，ELM)等機器學習算法快速發展，在預測領域的優越性突顯出來，逐步取代了移動平均法、自回歸移動平均法等傳統統計方法[10 - 11]。

早期機器學習算法難以處理時序數據相關性和動態特性，無法適應大規模訓練數據[12]。長短時記憶網絡(long short term memory, LSTM)是在循環神經網絡(recurrent neural network，RNN)[13]的基礎上發展而來的，擁有一定的長時記憶能力，可以解決RNN的梯度消失問題[14]。所以LSTM模型在負荷預測和風電功率預測領域得到了廣泛的應用。常規LSTM模型只能挖掘正向時序信息，有學者提出了雙向LSTM(bidirectional LSTM，BiLSTM)結構，它可以進行雙向時序關系的挖掘。文獻[15]使用LSTM網絡對風電場功率進行超短期預測，取得了比ANN和SVM更精確的效果。文獻[16]研究表明BiLSTM針對時間序列數據的預測效果優于單向LSTM。鑒于卷積神經網絡(convolutional neural network，CNN)在圖像處理領域上表現出的強特征提取能力，研究人員開始把CNN和LSTM組合使用。文獻[17 - 18]使用CNN自動提取歷史數據高維特征，使用LSTM網絡對多變量時間序列進行建模，比使用單一網絡具有更高的預測精度。

但CNN和LSTM的組合模型在風電功率預測的應用上仍存在以下不足：1)面對極端天氣時數據中的隱藏特征比良好天氣時更重要，功率波動時峰值隱藏的特征比平穩運行時更重要，而普通CNN結構無法辨別這些高維特征的差異性，導致重要特征有可能被忽略；2)LSTM和BiLSTM的時序信息挖掘能力，都是面對較短序列輸入時展現出的優勢，只適合處理時序數據中的局部相關性，當面對風電功率數據這種多維長序列時，存在容易忽略序列結構信息、難以解決長時依賴等問題[19 - 20]。

注意力機制[21]可以很好地解決上述問題，它本質上是一種加權機制，根據輸入數據對結果產生的影響賦予不同的概率權重，使重要特征不會因時間步長的延長而被忽略。本文提出基于雙重注意力機制的CNN-BiLSTM的風電功率預測模型，將注意力機制分別引入CNN和BiLSTM中，組成特征注意力模塊和時間注意力模塊。特征注意力模塊通過對CNN輸出結果進行加權分配實現對原始數據中重要特征的挖掘，并加強其影響。時間注意力模塊根據BiLSTM的隱藏層狀態中各時間節點對預測結果的影響提取重要的歷史信息，加強了對中長步長中相互依賴關系的學習。

本文主要開展的研究工作如下：1)將雙重注意力機制引入CNN-BiLSTM模型，以有效解決重要高維特征提取和時間序列長時依賴問題；2)使用貝葉斯優化對整個模型的超參數進行尋優，提高模型最優學習能力，避免人工調參依賴經驗、耗時耗力以及穩定性差等不足；3)分別用單步預測結果和多步預測結果對模型性能進行驗證，其中多步預測區別于常見的2步、3步預測，使用24步預測實現4 h前的超短期預測。

1 深度學習模型原理

1.1 CNN網絡

CNN模型[22]是當前深度學習中最流行的模型之一，利用卷積運算實現對原始數據更高維的表示，可以有效提取原始數據中的內部特征[23]。

CNN結構圖如圖1所示，標準的CNN由卷積層、池化層、全連接層組成。CNN結構計算公式如式(1)—(3)所示。

(1)

P=δ(C)+bp

(2)

H=φ(P×ws+bs)

(3)

式中：C和P分別為卷積層和池化層的輸出狀態；H為CNN結構輸出的特征向量；wc和ws分別為卷積層和全連接層的權重矩陣；bc、bp和bs分別為卷積層、池化層和全連接層的偏置向量；?為卷積運算；f(·)為卷積層激活函數，本文選取ReLU函數；δ(·)為池化方法，本文選取最大池化；φ(·)為全連接層激活函數，本文選取Sigmoid函數。

1.2 LSTM網絡

LSTM在RNN的基礎上增加了3個邏輯門控單元：遺忘門、輸入門、輸出門。LSTM可以保存數據狀態，實現在多個時間步長上穩定學習，有效建模序列的時間依賴關系[24 - 25]。LSTM網絡結構如圖2所示。

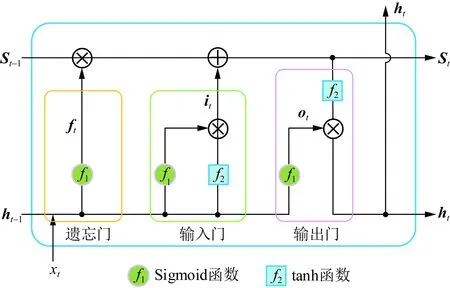
圖2 LSTM結構圖Fig.2 Structure of LSTM

輸入門負責選擇需要被保留的當前時刻t的狀態，遺忘門負責選擇需要被忘記的上一時刻t-1的狀態，輸出門負責選擇需要輸出給隱藏狀態ht的當前時刻狀態。LSTM網絡計算如式(4)—(8)所示。

it=Sigmoid(wixt+uiht-1+bi)

(4)

ft=Sigmoid(wfxt+ufht-1+bf)

(5)

ot=Sigmoid(woxt+uoht-1+bo)

(6)

St=tanh(wgxt+ught-1+bg)⊙it+St-1⊙ft

(7)

ht=tanh(St)⊙ot

(8)

式中：it、ft、ot、St和ht分別為輸入門、遺忘門、輸出門、記憶單元和輸出單元的狀態矩陣；wi、wf、wo、wg為不同邏輯單元對應本時刻輸入xt的權重矩陣，下標i、f、o、g分別表示輸入門、遺忘門、輸出門和記憶單元；ui、uf、uo、ug分別為不同邏輯單元對應上一時刻輸出ht-1的權重矩陣；bi、bf、bo、bg分別為不同邏輯單元的偏置向量；⊙表示矩陣中對應位置元素相乘。

1.3 BiLSTM網絡

BiLSTM[26]網絡本質上是一個雙層LSTM網絡，由正向LSTM層和反向LSTM層組合而成。在正向LSTM層中，輸入序列以順序形式輸入網絡進行訓練，挖掘數據的順序依賴關系。在反向LSTM層中，輸入序列以逆序形式輸入網絡進行訓練，挖掘數據的逆序依賴關系。這種結構可以對輸入數據進行雙向時序特征提取，進一步提高時序特征提取的全局性和完整性。BiLSTM的網絡結構如圖3所示。

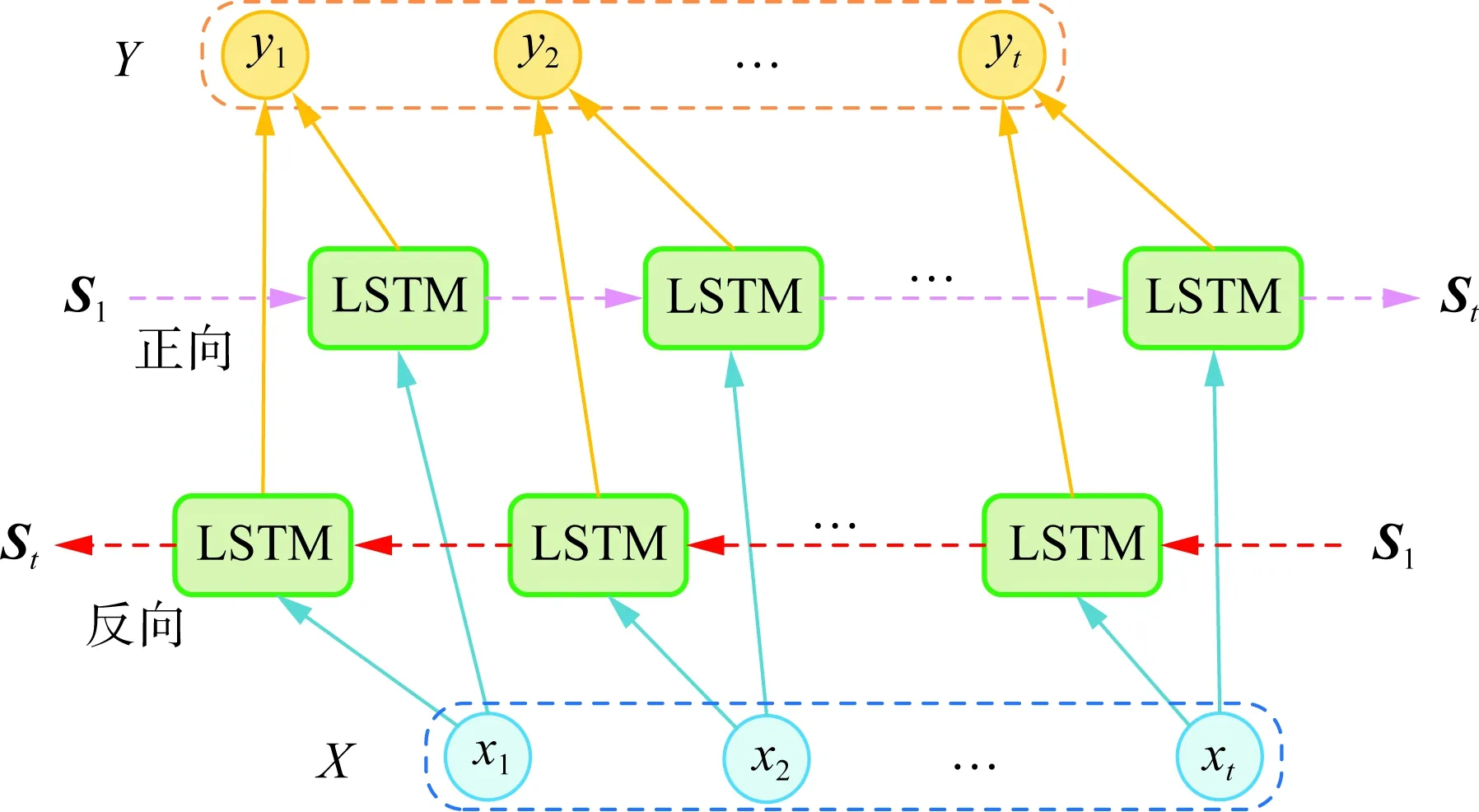
圖3 BiLSTM結構圖Fig.3 Structure of BiLSTM

1.4 注意力機制

注意力機制模型[27]的核心思想是通過合理分配不同輸入信息的注意力，為神經網絡中的隱藏層狀態賦予不同的權重，突出重要信息對結果的影響，提高模型預測準確率。注意力機制的權重分配計算可用式(9)—(10)表示。

et=uatanh(waht+ba)

(9)

(10)

式中：ht為t時刻神經網絡隱藏層狀態向量；et為注意力概率分布值；at為注意力得分；ua和wa為注意力權重向量；ba為注意力偏置向量。

2 基于雙重注意力機制的CNN-BiLSTM風電功率預測模型

風電功率數據中不僅包含歷史風電功率信息而且包含與之對應的歷史天氣信息，可將具有n個時段m種天氣特征的風電功率數據表示為1個n×(m+1)的矩陣X=[x1,x2,…,xn]T， 其中x=[p,c1,c2,…,cm]，p為功率數值，c為天氣數據。作為典型的多維時間序列數據，風電功率數據內部蘊含著歷史功率與未來功率的映射關系、歷史天氣與歷史功率的映射關系、歷史天氣與未來功率的映射關系以及各天氣特征的歷史與未來的映射關系。

針對這些復雜映射關系，本文提出一種基于雙重注意力機制的CNN-BiLSTM風電功率預測模型，具體結構如圖4所示。此模型采用encoder-decoder框架，特征注意力模塊作為編碼器，時間注意力模塊作為解碼器。特征注意力模塊由CNN網絡和注意力機制組合而成，CNN網絡憑借卷積操作和池化操作能夠充分挖掘數據中的高維特征，注意力機制對高維特征的權重進行訓練，確保關鍵特征發揮重要影響。時間注意力模塊由BiLSTM網絡和注意力機制組合而成。BiLSTM網絡能更好地學習時間序列數據中的周期特征和趨勢特征。注意力機制通過對隱藏狀態權重的訓練，自主選擇重要的歷史序列狀態信息，克服了BiLSTM網絡面對較長時間序列輸入時容易出現的信息丟失和梯度消失問題，突出了時序狀態對預測結果的影響。

圖4 模型結構圖Fig.4 Structure of model

2.1 特征注意力模塊

特征注意力模塊由CNN網絡和注意力機制組合而成。輸入數據經卷積層使其維度增加，然后經池化層壓縮參數量，再由全連接層將特征轉換為一維結構，最后經注意力機制分配權重完成重要特征的提取。此模塊采用雙層CNN結構，即由兩個卷積層和兩個池化層交替組成，將卷積層均設計為一維卷積結構。其結構可用式(11)—(17)表示。

C1=conv(X)

(11)

P1=pool(C1)

(12)

C2=conv(P1)

(13)

P2=pool(C2)

(14)

Hc=FC(P2)

(15)

af=Attention(Hc)

(16)

cf=afHc

(17)

式中：conv(·)表示卷積層計算，具體公式見式(1)；pool(·)表示池化層計算，具體公式見式(2)；FC(·)表示全連接層計算，具體公式見式(3)；Attention(·)表示注意力機制計算，具體公式見式(9)—(10)；af為特征權重向量；cf為特征注意力模塊輸出向量。

2.2 時間注意力模塊

輸入數據經特征注意力模塊編碼后得到隱藏狀態cf， 在encoder-decoder框架中稱其為中間語義。時間注意力模塊作為整個模型的解碼器，對中間語義cf進行解碼操作：將蘊含關鍵特征信息的cf通過BiLSTM雙向學習，捕獲序列內部時間變化規律；注意力機制根據歷史節點與結果的關聯程度，賦予BiLSTM輸出的隱藏狀態不同權重；最后經輸出層得到預測結果。其結構可用式(18)—(23)表示。

(18)

(19)

(20)

as,t=Attention(HB,t)

(21)

(22)

yt=Sigmoid(wrrt+br)

(23)

3 基于貝葉斯優化的預測模型超參數尋優

深度學習模型的超參數優化問題可以看作一個黑盒函數，我們只知道其輸入和輸出，不清楚其數學性質。深度學習模型的超參數優化問題與其他全局優化問題相比，其最大的特點是每一次函數評估都需要調用神經網絡訓練，每一次訓練短則十幾分鐘，長則幾個小時，所以訓練成本非常高。目前廣泛應用的群智能算法，例如粒子群算法、麻雀算法等，需要對優化函數進行初始化操作，并不斷更新初始化矩陣，這就意味著需要大量調用神經網絡進行訓練，極大地增加了尋優模型的訓練成本。因此，群優化算法并不適合深度學習模型的超參數尋優。貝葉斯優化(Bayesian optimization，BO)[28]使用貝葉斯定理可以充分利用之前函數的評估信息，根據目標函數的后驗分布，選擇下一個最有潛力的采樣點。BO可以實現通過較少的評估找到函數的全局最優解，對黑盒函數同樣可以達到很好的效果，適合深度學習模型的超參數尋優問題[29 - 30]。

貝葉斯優化算法通過概率代理模型對超參數的先驗概率進行觀測，從而獲得后驗概率分布。然后使用采集函數根據后驗概率分布得到下一個較優的超參數評估點。該算法的核心內容參見文獻[29]。預測模型的超參數優化流程如圖5所示。

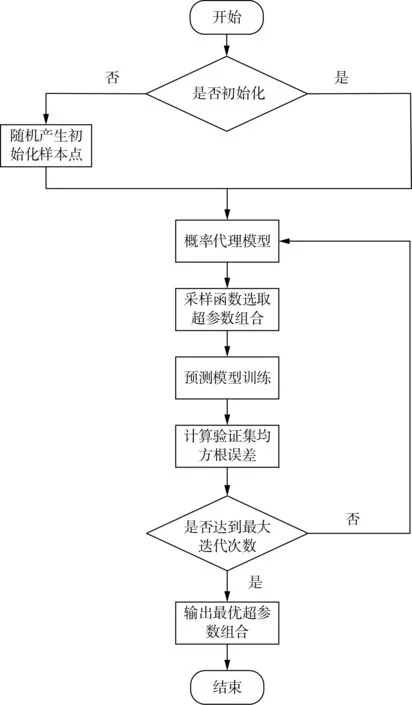
圖5 貝葉斯超參數優化流程圖Fig.5 Bayesian hyperparameter optimization flowchart

4 時間序列數據填充算法

由于新能源消納策略不夠完善，風電場實際運行時會接受電網調度產生棄風，這種人為不可預見因素的引入破壞了風電功率序列的規律性。本文采用文獻[31]所提時序數據填充方法，使用生成對抗網絡(generative adversarial network，GAN)對棄風數據進行填充。

生成對抗網絡主要由生成器和判別器組成，生成器致力于將一個服從高斯分布的隨機向量映射成一組逼真的新樣本，而判別器致力于判別輸入樣本的真假，二者構成一個零和博弈問題。文獻[31]所提方法采用WGAN結構，在搭建生成器和判別器的過程中使用一種針對時間序列的填充神經單元GRUI，能夠有效處理缺失時序數據，獲得其本質特征與缺失規律。將有缺失的時間序列數據和隨機向量輸入生成器，合成一份新樣本數據送入判別器判斷。當訓練到判別器輸出的準確率保持在50%時，說明生成器學習到了原始時間序列的規律，可以生成以假亂真的樣本。

將問題描述為最小化原始數據x與新生成樣本G(z)的差異，如式(24)所示。

(24)

式中：M為缺失標識矩陣；z為隨機向量；G(·)表示生成器；D(·)表示判別器；λ為超參數。

缺失值填充方式如式(25)所示。

ximpute=x·M+(1-M)·G(z*)

(25)

式中：z*為最優輸入向量。

5 算例分析

5.1 數據預處理

本文采用中國西北地區某風電場實際發電數據和天氣數據，選取2014年全年實測數據，包括風電功率、風速、風向、溫度，時間分辨率為10 min，風電場裝機容量為49.5 MW。此數據集全年丟失或無效記錄數據489條，數據完整率為99.07%，數據質量符合研究要求。

針對原始數據集中的完全棄風數據，采用第4節所述基于生成對抗網絡的時間序列數據填充方法進行填充，模擬風場不接受調度的情況下最有可能的發電情況，可以有效保護風電數據的完整性和規律性。

為了方便神經網絡的訓練，通常需要將數據進行歸一化處理，功率、風速、溫度數據采用式(26)的max-min歸一化方法將數據歸一化至[0,1]區間。風向則采用三角函數歸一化方法，即取風向的sin值和cos值共同表征風向信息[32]。

(26)

式中：x為實際值向量；xmax和xmin為x的最大值和最小值；x′為歸一化向量。

5.2 誤差指標

本文選取歸一化均方根誤差(normalized root mean square error, NRMSE)和確定系數(R-squared, R2)作為評估預測結果精度的指標，計算公式分別見式(27)和式(28)。NRMSE可以衡量預測的整體誤差，其值越小預測結果越準確。R2可以表示兩條曲線的相似程度，其值越近1則預測效果越好。預測領域常用的誤差指標還有平均百分比誤差(mean absolute percentage error，MAPE)，但是風電功率預測與其他預測不同點在于風電功率的實際值存在功率為零的時刻，根據式(29)所示的MAPE計算公式，會出現分母為零的情況，故MAPE不適合作為風電功率預測的誤差評價指標。

(27)

(28)

(29)

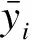
5.3 單步預測結果分析

本文將數據集的60%設置為訓練集，20%設置為驗證集，20%設置為測試集。采用時間步長為10步的單步預測方式，即輸入t-10至t時刻的歷史多維數據，預測t+1時刻的功率值。本小節首先進行了輸入歷史數據的單步預測實驗，然后進行了歷史數據結合數值天氣預報(numerical weather prediction，NWP)信息的單步預測實驗，從這兩個角度對本文所提方法進行驗證。為了驗證每一層注意力機制和BO方法的有效性，將本文所提模型與BiLSTM、CNN-BiLSTM、加入時間注意力的CNN-BiLSTM-Attention以及未經BO超參數優化的CNN-BiLSTM-dual-Attention模型進行對比試驗。每次實驗均在訓練集上訓練模型，在驗證集上調整模型超參數，固定超參數后，在測試集上驗證結果。預測結果經反歸一化后計算NRMSE和R2的值，實驗結果如表1—2、圖6—7所示。

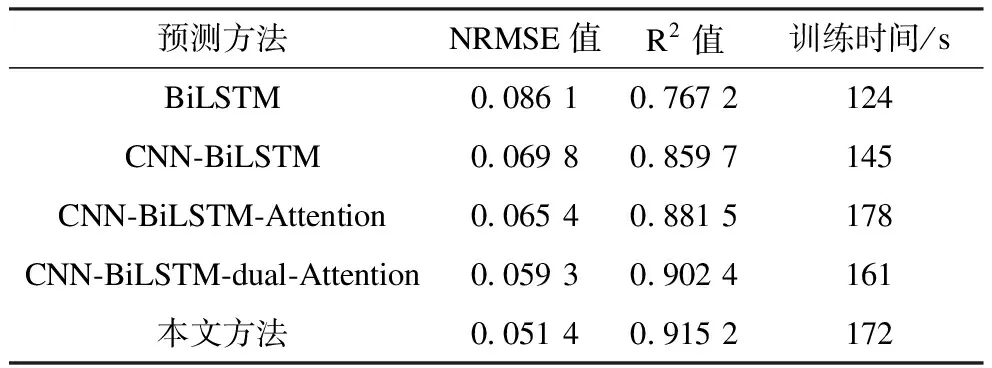
表1 未結合NWP的各模型單步預測結果對比Tab.1 Single-step predication results of different models without NWP

表2 結合NWP的各模型單步預測結果對比Tab.2 Single-step predication results of different models with NWP

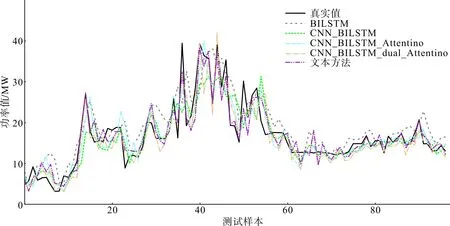
圖6 未結合NWP的各模型單步預測結果對比Fig.6 Single-step predication results comparison of different models without NWP

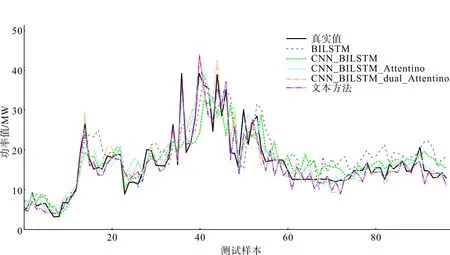
圖7 結合NWP的各模型單步預測結果對比Fig.7 Single-step predication results comparison of different models with NWP

本文所提基于BO超參數優化和雙重注意力機制的CNN-BiLSTM模型比其他模型具有更高的預測精度。從表1的對比結果可以發現：相比普通的BiLSTM模型，具有特征提取功能的CNN-BilSTM預測模型的NRMSE值下降了0.016 9，R2值提升了0.092 5，這是由于CNN層能夠對復雜的多維風電功率數據實現有效的特征提取；加入時間注意力后的CNN-BiLSTM-Attention模型的NRMSE值下降了0.004 4，R2值提升了0.021 8，可見時間注意力機制能夠有效提取到重要的時間節點信息；具有雙重注意力機制的CNN-BiLSTM-dual-Attention模型比僅具有時間注意力的模型的NRMSE值下降了0.006 1，R2值提升了0.020 9，這是由于注意力機制對CNN提取的高維特征進行篩選，突出了重要特征的影響；本文所使用的基于BO超參數優化和雙重注意力機制的CNN-BiLSTM模型預測結果的NRMSE值下降了0.007 9，R2值提升了0.012 8，說明BO超參數優化可以尋找到一組最優的超參數，得到更好的預測效果。

從圖6中可以更直觀地發現：基準模型BiLSTM的預測結果(BiLSTM曲線)整體表現最差；其他模型的預測結果在風電功率平穩的區間表現較為接近， CNN-BilSTM模型預測結果(CNN-BilSTM曲線)和只具有時間注意力模塊的預測模型結果(CNN-BilSTM-Attention曲線)在原始數據波動幅值較大的區間的預測結果偏差較大，而且對于極值的預測存在不同程度的滯后現象；基于雙重注意力機制的CNN-BilSTM模型(CNN-BilSTM-dual- Attention曲線)對波動區間的預測效果更好，可以有效預測波動區間的極值，并且改善了滯后現象。這是由于所提模型的特征注意力模塊和時間注意力模塊解決了高維特征篩選問題和時間序列的長時依賴問題，這兩個模塊的配合使用可以有效預測下一個時間節點的趨勢和波動幅度，有利于提高整體預測的精度。基于BO超參數優化和雙重注意力機制的CNN- BilSTM模型(本文方法曲線)比未經超參數優化的模型(CNN-BilSTM-dual-Attention曲線)表現出了更好的效果，說明BO算法可以找到一組優秀的超參數。

從表1、表2和圖7中可以發現：所有測試模型在結合NWP信息后均比未結合NWP信息時表現更好，說明所有模型均可以有效利用NWP信息。本文提出的基于BO超參數優化和雙重注意力機制的CNN-BiLSTM模型在結合NWP的單步實驗中的表現仍然是最優秀的，其NRMSE值為0.044 2，比未結合NWP的模型下降了0.007 2，R2值達到0.938 6，比未結合NWP的模型提升了0.023 4。

本文所提的基于BO超參數優化和雙重注意力機制的CNN-BilSTM預測模型可以捕捉風電功率序列的波動性，對極值的預測更加準確，其單步預測效果比其他算法的預測精度更高。

5.4 多步預測結果分析

在用單步預測驗證本文所提算法的有效性后，本節從實際應用角度出發，結合NWP信息進行4 h前的超短期風電功率預測。將未來4 h的NWP數據(包含風速、風向、溫度)與歷史風電數據共同輸入模型，輸入時間步長設為24，使用BO算法重新選擇適應多步預測的超參數，預測未來4 h(24個預測點)的風電功率。將本文模型與CNN-BiLSTM模型進行對比實驗，實驗結果如表3和圖8所示。

表3 結合NWP的各模型多步預測結果對比Tab.3 Multi-step predication results comparison of different models with NWP

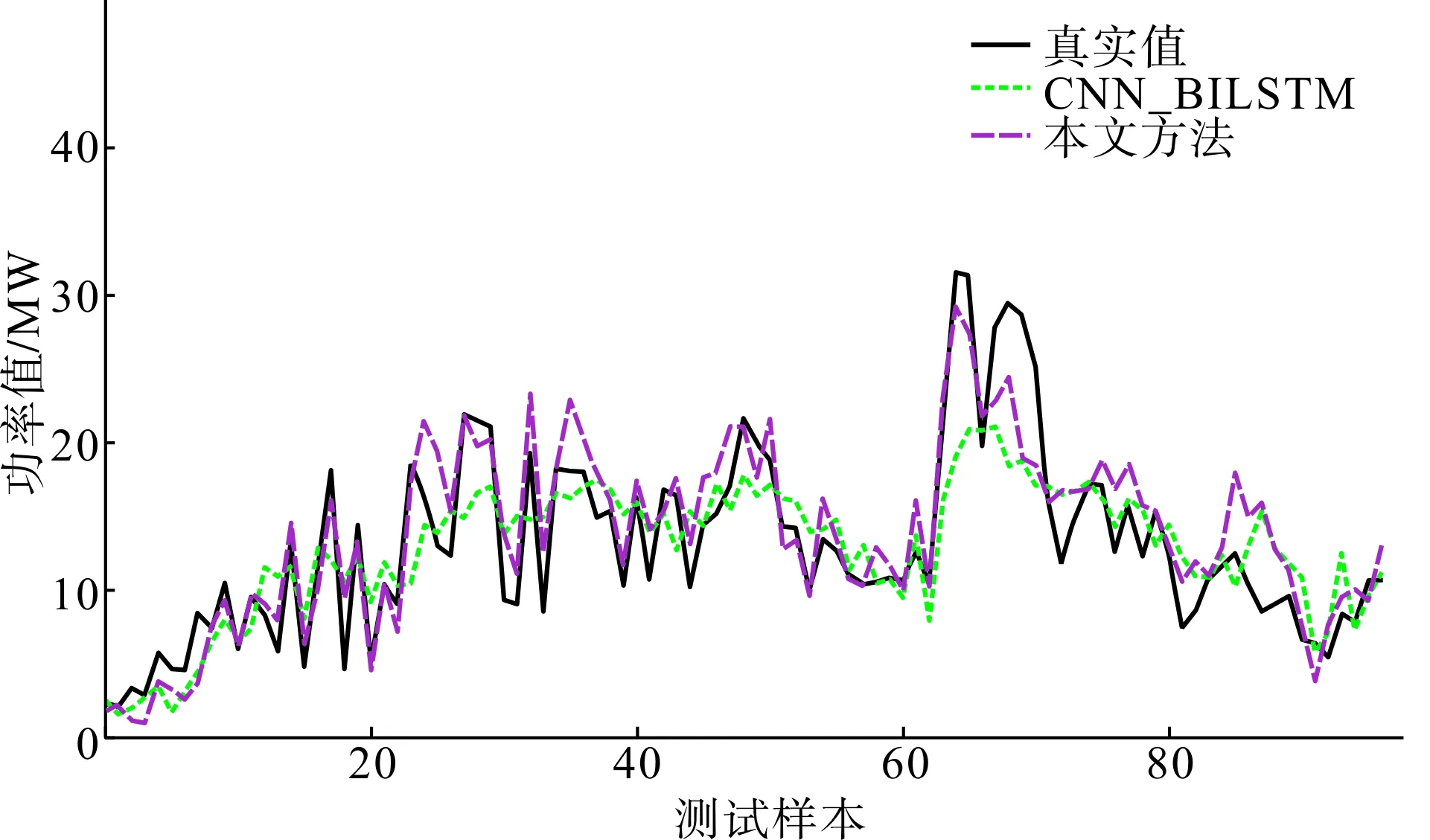
圖8 結合NWP的各模型多步預測結果對比Fig.8 Multi-step predication results comparison of different models with NWP

本文所提的基于BO超參數優化和雙重注意力機制的CNN-BiLSTM模型的多步預測結果比CNN-BilSTM模型精度更高。從表3中可以發現本文模型比CNN-BilSTM模型預測結果的NRMSE下降了0.025 7，R2提升了0.118 3；從圖8中可看出，CNN-BiLSTM模型(CNN-BilSTM曲線)對風電功率峰谷值預測能力較差，本文所提預測模型結果(本文方法曲線)對預測時段的風電功率波動情況預測效果更好。這是由于時間注意力模塊在步長較長的預測模型中很好地加強了BiLSTM的長時記憶能力，并能更夠篩選出更重要的時間節點進行預測。這個多步預測實驗說明：在結合NWP信息的超短期風電功率預測方面，本文所提模型同樣有效。

5.5 超參數優化結果分析

使用Python的Bayesian Optimization庫實現對第2節所提基于雙重注意力機制的CNN-BiLSTM預測模型的超參數尋優，并與常用的群智能尋優算法性能進行比較。

在驗證集上對單步預測模型進行超參數尋優，以最小化預測結果的NRMSE為優化目標，針對學習率、迭代次數、卷積核大小和數量、BiLSTM神經元數量、全連接層節點數等超參數，分別使用BO、粒子群優化(particle swarm optimization，PSO)[33]、麻雀算法(sparrow search algorithm，SSA)[34]、平衡器優化(equilibrium optimizer，EO)[35]進行尋優實驗，結果如表4所示。

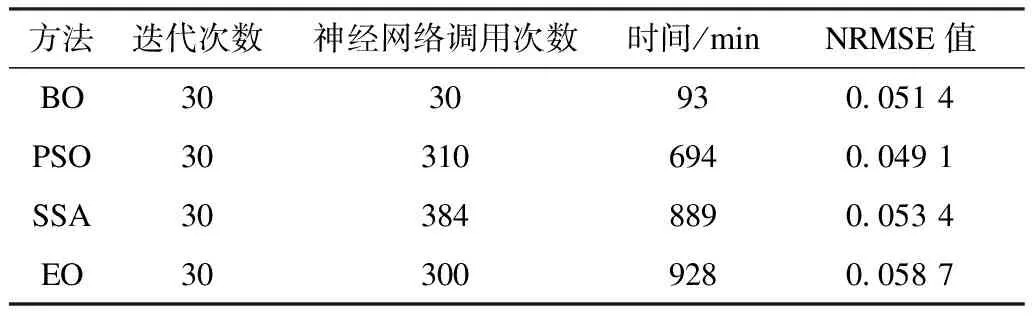
表4 超參數尋優結果Tab.4 Results of hyperparameter optimizations

表4的實驗結果表明使用貝葉斯優化算法對深度學習模型進行超參數優化具有訓練成本小、收斂速度快的特點。在4種優化方法中誤差最小的是PSO算法，BO算法精度位列第二。BO算法的誤差僅比PSO算法高出了0.23%，但耗時卻比PSO算法降低了86.6%。BO算法的精度在與常見的群智能優化算法保持在同一水準的情況下，極大地縮短了運算時間。

6 結語

為解決一般模型無法有效提取多維風電歷史數據的重要特征以及時間序列的長時依賴問題，以提高風電功率超短期預測的精度，本文提出了一種基于超參數優化和雙重注意力機制的CNN-BiLSTM風電功率超短期預測模型，模型使用CNN與注意力機制結合的特征注意力模塊提取多維風電歷史數據重要特征，再通過BiLSTM與注意力機制結合的時間注意力模塊對特征向量進行動態時序建模，最后通過BO優化方法選擇模型的最優超參數，以發揮模型的最佳性能。

通過算例分析發現本文模型很好地解決了多維數據重要特征的自動提取和時間序列的長時依賴問題，也解決了人工調參耗時長、效果不穩定的問題，驗證了所提模型的有效性和穩定性，與其他方法相比本文所提模型具有更高的預測精度。

后續工作將研究不同模型在風電功率處于不同波動狀態和不同出力水平下的預測效果，從而通過組合預測實現更高的預測精度。