電力現貨市場出清價格預測誤差風險分析

趙越，劉思捷，白楊，高海翔，龔超，蔡秋娜，王子石，龔昭宇

(1.廣東電網有限責任公司電力調度控制中心，廣州510060；2. 廣東電網有限責任公司市場安全經濟運行與市場化調度重點實驗室，廣州510230；3. 北京清能互聯科技有限公司，北京100084)

0 引言

放松管制、引入競爭已成為電力市場建設的重要任務，目前國內8個現貨試點均已進入結算試運行階段[1 - 2]，形成具有時間及空間特性的現貨市場出清價格。準確的出清價格預測對系統運營商及市場主體具有重要意義[3]，系統運營商需要通過預測價格對市場風險進行預警及預控，發電廠、售電公司則需要通過預測價格評估交易風險、制定競價策略。

現有的現貨價格預測方法主要可分為數據驅動和模擬出清兩類[4]。數據驅動即挖掘出清價格與自身及其他相關因素規律，并使用統計學習、人工智能等方法建立并擬合回歸模型。文獻[5]將外生變量引入自回歸模型，使傳統時間序列模型可考慮其他相關因素影響；文獻[6]使用隨機森林模型預測現貨出清價格，并形成一套科學的輸入特征篩選和模型調參方法；文獻[7]分析了高比例風電下影響電價的主要因素，使用長短期記憶網絡(long short term memory，LSTM)算法構建電價預測模型。數據驅動方法在風電[8]、氣象[9]及負荷預測[10 - 11]等領域也應用廣泛，具有較強的通用性。然而，不同于上述領域，現貨出清價格具有明確的計算模型(安全約束經濟調度，security constrained economic dispatch，SCED)，模擬出清法即通過模擬該計算模型間接得到出清價格。文獻[12]通過預測負荷、發電、邊界條件等信息，基于SCED模型和多參數規劃得到節點電價和線路阻塞的概率預測結果。

無論是對預測方法本身的改進還是評價能否實際應用，均需要基于對預測誤差的評估。現有文獻中的價格點預測評估指標與其他預測領域相同，都是基于時段平均與絕對值的準則，如絕對值誤差(absolute error, AE)、平均絕對值誤差(mean absolute error, MAE)[13]、平均絕對值百分比誤差(mean absolute percentage error, MAPE)[14]、均方根誤差(root mean square error, RMSE)[15]等，認為預測效果可以隨上述指標的減小而改善。

然而傳統指標應用于價格預測誤差分析，存在以下不足：1)系統運營商、發電商、售電商等主體預測價格用途不同，傳統指標沒有基于特定用途分析誤差影響；2)不同主體在各時段交易電量不同，采用平均準則無法衡量不同時段預測誤差帶來的經濟風險；3)若出現傳統指標在模型間各有優劣的情況，將導致預測模型難以選擇。

相比傳統評估指標，風險評估指標可以考慮在工程應用中由誤差導致的實際后果。如文獻[16]提出了風電功率預測誤差的風險評估指標，其認為風電功率預測正誤差與負誤差對系統可靠性影響不同，誤差絕對值與經濟性影響也不同，故采用預測事件概率與事件發生損失的積分作為模型評價指標。文獻[17]提出使用負荷預測誤差對系統機組組合成本的影響作為負荷預測模型評價依據。文獻[18]分析了電價預測誤差對市場參與者的經濟影響。但目前仍未有在電價預測領域統一建模、針對不同決策主體分別考量其風險的分析方法。

綜上，本文提出價格預測誤差風險評估指標，該指標考慮了市場主體因價格預測誤差產生的不同經濟后果，針對主體各時段交易電量賦予不同權重，可以準確反映風險成本。本文所提指標綜合衡量不同決策主體因預測誤差帶來風險，可以給予各類市場主體可靠的模型評估及選擇參考。

1 預測誤差評估指標分析

本節對預測領域常用的誤差分析指標進行梳理和對比，并對其進行總結并分析其不足后，歸納出一般化的指標設計原則。在此基礎上，提出一般化誤差評估指標模型。

1.1 常用預測誤差評估指標

為具體說明，本文例舉4種常見的點預測誤差評估指標，具體如下。

(1)

然而現實預測任務大多數需要評估多時段的預測結果，絕對值誤差指標不具備數據降維能力，因此不適用于多時段場景。

2)平均絕對值誤差(EMAE)。通過在EAE基礎上取誤差序列的平均值，可得到EMAE指標。

(2)

式中T為時段數。EMAE適用于多時段場景，因具有計算簡單、含義明確等特點已在預測任務中廣泛使用。但其衡量標準基于待預測量真值，難以直接對比模型在不同任務中的預測效果。

3)平均絕對值百分比誤差(EMAPE)。通過對每一個誤差值除以其真值并記百分比，可得到EMAPE。

(3)

相比絕對值指標，EMAPE對誤差比例有更直觀認識，可以衡量一個模型在不同任務中的預測效果。但當真值序列接近0時該指標存在數值問題[19]。

4)均方根誤差(ERMSE)。ERMSE引入非線性變換計算序列相似度。

(4)

相比其他使用1范數損失處理正負誤差的指標，在ERMSE中，2范數損失通過平方運算放大了預測值與真值之間的距離，且具有可微、可導的性質。

此外針對不同預測場景，一些學者也使用了季節性平均絕對標準誤差(seasonal mean absolute scaled error, SMASE)、均方差標準誤差(root mean square scaled error, RMSSE)等作為模型評估依據[20]。

1.2 預測誤差評估指標設計原則

圖1展示了在兩時段預測任務中預測誤差與4種常見指標的關系。本節以此為例總結在設計誤差評估指標時，除唯一性與單調性以外，仍需要考慮的幾個因素。

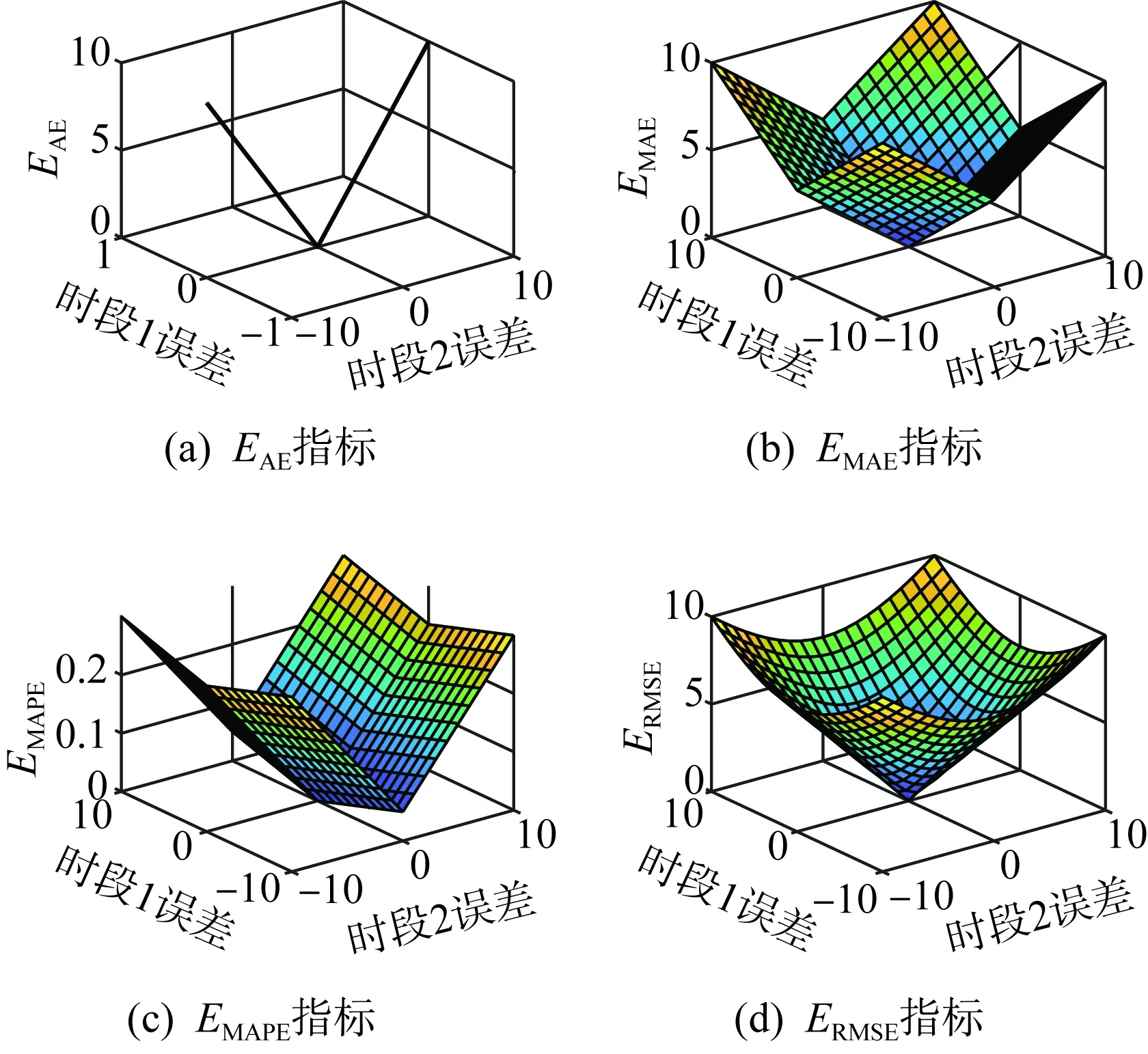
圖1 常見誤差評估指標幾何表示Fig.1 Geometric representation of common error assessment indicators

2)多樣本權重：在多樣本任務中，衡量樣本集內各子樣本量化到指標中的標準是否一致。EMAE、ERMSE即假設子樣本無差異，EMAPE根據樣本真值設置權重，一些綜合評價指標也會根據日類型(工作日、節假日)設置權重，以凸顯任務偏好。若多樣本權重不同，圖1曲面在x軸與y軸投影具有不同形狀，如圖1(c)EMAPE。

3)誤差值非線性程度：反映指標值隨誤差值改變而改變的程度。若存在常數C，使dφ/de=C， 則稱誤差值為線性的。ERMSE通過對誤差序列平方和開根引入一定非線性，可使指標對單個誤差較大值更為敏感，在圖1(d)中誤差與指標值的關系也從線性條件下的平面變為曲面。

1.3 一般化誤差評估指標模型

綜合1.2節評估指標設計原則，提出針對時間序列點預測的一般化誤差評估指標如式(5)所示。

(5)

式中：kt為t時刻正負誤差權重，其取值如式(6)所示；et為t時刻預測誤差；wt為t時刻的樣本權重；m為誤差非線性系數；α(·)為指標激活函數。

(6)

式中：kt+、kt-分別為t時刻的正誤差權重值、負誤差權重值。

樣本權重主要衡量不同時段預測誤差的影響，如對需求側用戶可以使用預測用電量作為權重系數，在用電量低的時段，預測偏差對決策及成本影響較小，因此誤差權重較低；在用電量高的時段，較小的預測偏差即可能對其購電決策及最終成本帶來較大影響。非線性系數主要影響較大預測誤差的敏感程度，若單位預測偏差對市場主體錯誤決策導致的收益損失呈線性關系，則該項取1；若小范圍的誤差對決策影響不大，而較大誤差會導致更大損失，此時即可取2以上的非線性系數。激活函數用以控制指標的值域取值大致范圍，一般有開根、除以序列數等操作。

設計指標時可根據具體應用場景將一般化誤差評估指標中的參數/激活函數設置為固定值/確定函數。可以看出1.1節所列幾種常用指標均為一般指標參數及激活函數取值不同時的簡化形式。下一節將討論針對現貨出清價格預測任務，各決策主體應如何根據自身需求選取指標參數。

2 現貨出清價格預測誤差風險評估指標

從不同主體預測電價的動機不同、傳統指標難以有效反映購電成本兩方面舉例說明風險評估指標存在的必要性，并分別從運營商和不同市場主體的預測電價使用場景及決策思路闡述指標設計思路并給出指標數學模型，最后總結上述風險指標的共性特點。

2.1 風險評估指標的必要性

現貨市場交易會產生日前電價與實時電價，日前電價用以結算日前交易競價空間內未被中長期合約覆蓋的電量，實時電價則用以結算實際用電量與日前中標電量的偏差部分。對系統運營商而言，預測出清價格可以作為事前風險評估體系的一部分，用以判斷系統是否存在高峰價格風險及分析潛在的市場力被動用的可能性，在該場景下不需要關心價格在正常范圍內存在的預測誤差；對發電商而言，預測現貨出清價格可以作為其對中長期合約的價格錨定，也可作為日前申報時的決策依據，而就評價預測模型而言，發電商更關心預測誤差對其實際收益產生的影響；而對售電商，在采用用戶側報量不報價及統一結算點電價結算的模式下[21]，售電商博弈空間在通過預測日前與實時價格高低確定其申報策略，因此更關心日前及實時預測結果是否會改變其申報傾向；用戶則更在意預測誤差是否會改變其用電計劃進而是否影響購電總成本。

另一方面，在市場主體充分博弈的市場中，現貨價格難以準確預測，各類預測模型由于數學機理不同可能產生不同的誤差分布，此時依據傳統指標評估結果選出的“最佳模型”未必對所有決策主體都是最佳的。文獻[18]采用某工業用戶購電成本與MAPE誤差評估指標的關系形象說明該問題：如圖2所示，虛線表示將該用戶42天內的電價預測誤差MAPE值由高到低排列，柱形表示用戶當天實際購電成本比理想購電成本高出的比例。可以發現更低的MAPE指標并不一定能帶來購電成本的降低。

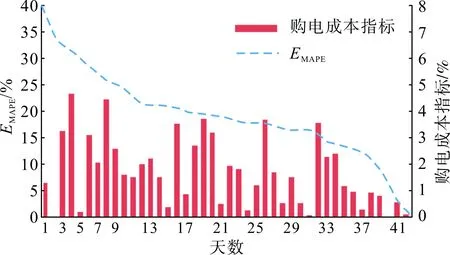
圖2 購電成本與MAPE值關系示意Fig.2 Relationship of electricity cost and MAPE value

因此，對于價格預測不同的使用場景，更應該關注預測誤差對市場風險、主體利益的影響，從而設計更符合決策主體需求的誤差評估指標，而本文認為的風險指某事件發生導致結果偏離預期的程度。

2.2 系統運營商指標設計

考慮系統運營商預測出清價格作為其事前風險評估體系的一部分[22]，需要重點關注以下3種情況：1)交易電量大；2)結算價格高；3)預測誤差大。交易電量大意味著相同數值的價格預測誤差對系統總成本的影響更大，因此指標應更關注預測模型在交易電量大時段的準確性；結算價格高是指事前風險預警體系中的一項重要內容為高價預警，而同樣的預測誤差發生在高價時段的負面影響顯然就高過低價時段，因此指標對高價時段的敏感度應低于低價時段；預測誤差大是指相比于多個時段的小誤差，一個時段的大誤差更容易對主體釋放錯誤的市場信號，因此在誤差之和相等的情況下，指標應更關注少量單個誤差值更大的情況。

考慮上述因素，在設計運營商誤差評估指標時，通過以下方法將上述3點因素計入指標：1)在樣本權重中加入市場化交易電量，提高高交易電量時段樣本的權重；2)在樣本權重中計入價格真值，提高高價時段樣本的權重；3)對各時段誤差值引入2階非線性系數，提高高誤差時段誤差值對指標的影響。所設計系統運營商指標φISO如式(7)所示。

(7)

wex,t=λ(pt)·λ(dt)

(8)

式中：wex,t為t時刻的運營商樣本權重；dt為t時段內市場化交易電量；函數λ(x)表示對x在樣本集X內進行min-max歸一化。

(9)

此外，開根號無實際物理涵義，一般是存在取平方操作時為避免指標數值過大的配套數值處理方法，本文設計指標沿用該處理方法。

2.3 發電商指標設計

若不考慮發電商在現貨市場中的投標策略及其對出清價格的影響，僅從事后角度評價電價預測誤差對發電商收益的影響，可發現單位預測誤差的收益影響與發電商在該時段的結算電量有關，故在評價發電商使用的電價預測模型時，可引入以預測價格結算的電量作為樣本權重，使指標值反映模型因預測不準對發電商預期收益造成的偏差。發電商誤差風險指標如式(10)所示。

(10)

式中：k為正負誤差權重，取k+=k-=1；樣本權重wgen,t設置為以該價格結算的電量，如預測日前電價時使用日前中標電量，預測實時電價時使用實時偏差電量。

該指標適用于以報量報價方式直接參與電能量市場并采用分時結算機制的發電機組，若機組暫未直接參與市場或以自調度方式參與市場，則其沒有預測現貨出清價格并參與博弈的需求。

2.4 售電商指標設計

在國內現貨試點實踐中，考慮到需求側相對成熟性及抗風險能力較弱，多采用報量不報價、用戶統一結算電價的方式(廣東、山西和山東均采用該方式)，此時售電商在參與現貨市場博弈時主要根據日前與實時價差改變申報策略，如預測實時電價高于日前電價，則在日前多申報電量，在實時市場售出套利。

因此，可將售電商的這種博弈特性引入對預測模型的性能評價指標中，在評估日前電價預測模型時可采用實時價格作為標尺設置樣本權重，僅將預測誤差可能導致售電商申報方向錯誤從而產生虧損的部分計入指標，定義售電商誤差風險指標為：

(11)

式中：k為正負誤差權重，取k+=k-=1；樣本權重wseller,t取值如式(12)所示。

(12)

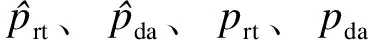
售電商指標φseller主要關注預測誤差是否會改變其利用日前與實時電價價差套利的申報策略，若預測誤差對其申報策略不會產生影響，則售電商對該誤差關注度較低；若會產生影響，則將其反映至風險指標中。

2.5 需求側用戶指標設計

考慮在需求側報量不報價及統一結算點電價結算的模式下，需求側用戶作為價格接受者，日前申報決策模型為：

(13)

式中：b為所有時刻負荷申報量集合；bt為t時刻負荷申報量；ζ為相關約束條件。該模型目的為通過改變申報量使預期購電成本最低。用戶實際購電成本為。

(14)

若能獲得完全準確的電價預測結果，可獲得用戶理想購電成本：

(15)

進而，將理想購電成本與實際購電成本的差值稱為價格預測誤差成本。

cerror=cactual-cideal

(16)

注意到誤差成本本身即可作為預測模型評估指標，但具有建模復雜、需要求解優化等缺點，本文對該指標進行一定簡化，在事后評估階段采用實際負荷申報量替代式(15)中的準確電價申報量，使需求側用戶誤差風險指標可以近似價格預測誤差成本。

(17)

式中wbid,t為t時刻的實際負荷申報量。需求側用戶指標φuser反映預測誤差對用戶實際購電成本產生的影響，一定程度上能反映數值誤差背后的經濟特性，相比傳統指標更具現實意義。

此外，按照2.1節所述存在常規價格預測誤差指標的減小不一定使主體收益提高(如圖2所示)的情況，發電商或售電商均可使用價格預測誤差成本作為模型評估指標，考慮到發電商及售電商決策模型相對復雜，本文直接闡述其指標設計思路和使用場景。

2.6 誤差風險評估指標特點

在現貨市場環境下出清電價具有較高不確定性，準確預測十分困難，而不同電價預測方法由于模型及數據層面的局限性，總會存在不同的誤差分布特性，預測指標的價值在于將上述高維的誤差分布映射至一維，從而使用戶能對比不同模型性能、選取最佳模型進行使用。然而，傳統預測指標僅考慮了誤差值的部分“數值特性”，沒有考慮不同用戶的實際用途差異及對應的“經濟特性”，使用傳統預測指標可能無法有效選取最佳模型。基于該問題，本文對誤差數值特性及其背后意義進行歸納總結，并分別針對系統運營商、發電商、售電商和需求側用戶在預測現貨出清價格時的不同目的，設計了不同的誤差分析指標，所提指標相比傳統指標具有如下優勢。

1)針對各主體不同交易行為設計指標數學模型，運營商、發電商、售電商等主體可根據預測價格用途的不同選取指標參數；

2)指標根據各時段交易電量設計不同權重，可以準確考量交易電量較高時段更大的經濟風險，同時使指標能考慮誤差的經濟特性；

3)指標確定后評價結果具有唯一性，不會出現多個傳統指標共同評估時可能出現的結果矛盾。

3 算例分析

本節中，3.1節說明算例概況、電價預測模型及預測結果，3.2節分析傳統評估指標評估結果及其不足，3.3—3.4節分別從指標數值一致性、對各主體不同需求的可定制性和對用戶實際決策收益的提高3個方面論述本文所設計指標的有效性。

3.1 算例說明

本文以廣東現貨市場2020年8月連續結算試運行電價數據為基礎，預測統一結算點日前價格，其余使用到的電價采用真實值，并以某電廠、某售電公司中標電量作為評價依據，最后建立工業用戶購電決策模型，驗證本文所提風險評估指標的有效性。本文算例中，電價預測部分基于Python及Tensorflow實現，優化問題部分基于Yalmip建模并調用Cplex求解。采用某電廠所接220 kV母線作為發電側結算節點，統一結算點作為用戶側結算節點，結算周期為1 h，統一結算點電價曲線見附錄圖A1。可以看到日前電價序列呈現一定的日、周周期性，價格整體水平與實時電價較為契合，但部分時段實時電價會出現日前電價沒有的價格尖峰。

算例將對比4種常見的電價點預測方法(M1—M4)的誤差指標，具體如下。

1)M1：相似日法[23]。周二—周五使用前一日價格作為預測值，周六—次周一使用上周同日價格作為預測值。

2)M2：SARIMA時間序列預測模型，對各時刻單獨建模，共24個模型，模型參數由AIC準則[24]確定。

3)M3：ANN神經網絡，使用前兩日48個時刻價格作為輸入，預測日24個時刻價格作為輸出。網絡有50節點隱藏層，采用ReLu激活函數和sgd優化器，迭代200次。

4)M4：LSTM神經網絡，使用前23個時刻和該時刻前7天對應時刻電價作為輸入，該時刻電價作為輸出。網絡由200節點LSTM層和1層全連接層構成，采用ReLu激活函數和adam優化器，迭代100次。

采用8月1日—8月30日數據作為訓練集，8月31日數據作為測試集，各方法預測結果對比如圖3所示。可以看到由于日前價格較平穩的周期特性，M1預測曲線形狀與真值較為相似，但存在凌晨至下午整體偏高、傍晚整體偏低的情況。由于訓練數據量過少，基于數據驅動的M2—M4相較M1并未體現直觀優勢，M2、M4均未準確預測清晨至清晨的價格低谷，M3給出了過低的預測值(甚至低于最低限價，但本算例僅考慮模型輸出值，不做二次處理)，M4僅在價格尖峰時段預測精度較高。

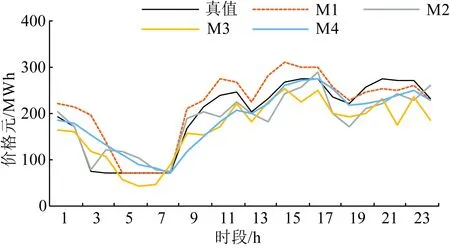
圖3 日前價格點預測結果對比Fig.3 Comparison of point forecasting results of day-ahead price

3.2 傳統評估指標結果分析

各傳統評估指標對3.1節算例的預測誤差指標如表1所示，各指標排序如圖4所示。由表1可知，在最常用的3種指標中，MAE評估的最佳模型為M4，其指標值為26.38；MAPE和RMSE評估的最佳模型為M2，其指標值分別為17.53與32.87。從圖4中可以看到，在5個指標中，有3個認為M2方法預測最小，但有2個認為M2排序第三；有2個認為M4方法預測誤差最小，其余指標中M4排序第二或第三。

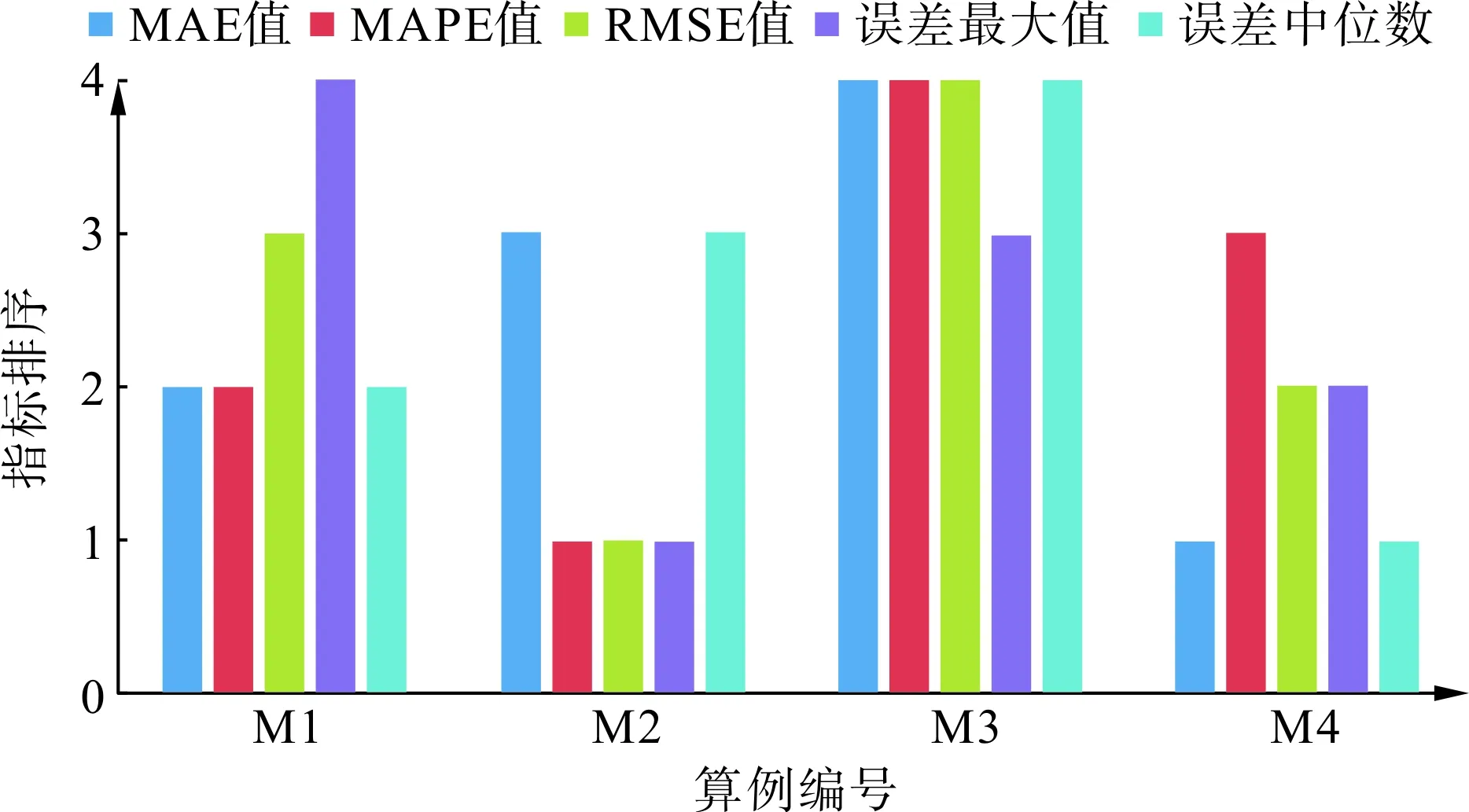
圖4 傳統誤差評估指標排序Fig.4 Rank of traditional error indexes

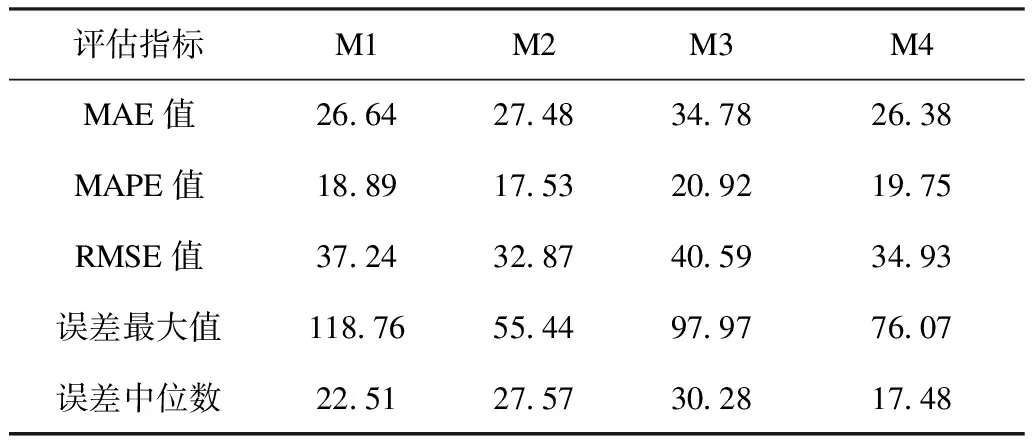
表1 傳統誤差評估指標結果Tab.1 Comparison of traditional error indexes

可以看到，采用傳統指標分析預測誤差，出現了各指標出現歧義，導致難以選取最佳預測模型的情況。若根據投票原則選取M2為最佳模型，會發現其在系統運營商、發電商使用場景中都產生了更大的風險偏差(見3.3節)，可見采用傳統指標可能引發錯誤的模型選取結果。

3.3 風險評估指標結果分析

本節分別應對系統運營商、發電商、售電商的預測價格使用場景，計算各場景的風險評估指標。

1)場景1：系統運營商視角如式(7)—(9)所示，設置dt為預測日日前競價空間；

2)場景2：發電商視角如式(10)所示，wgen,t取機組日前中標電量；

3)場景3：售電商視角如式(11)—(12)所示，不計實時電價預測誤差。

4)場景1—2使用的競價空間、合約分解系數如圖5所示。

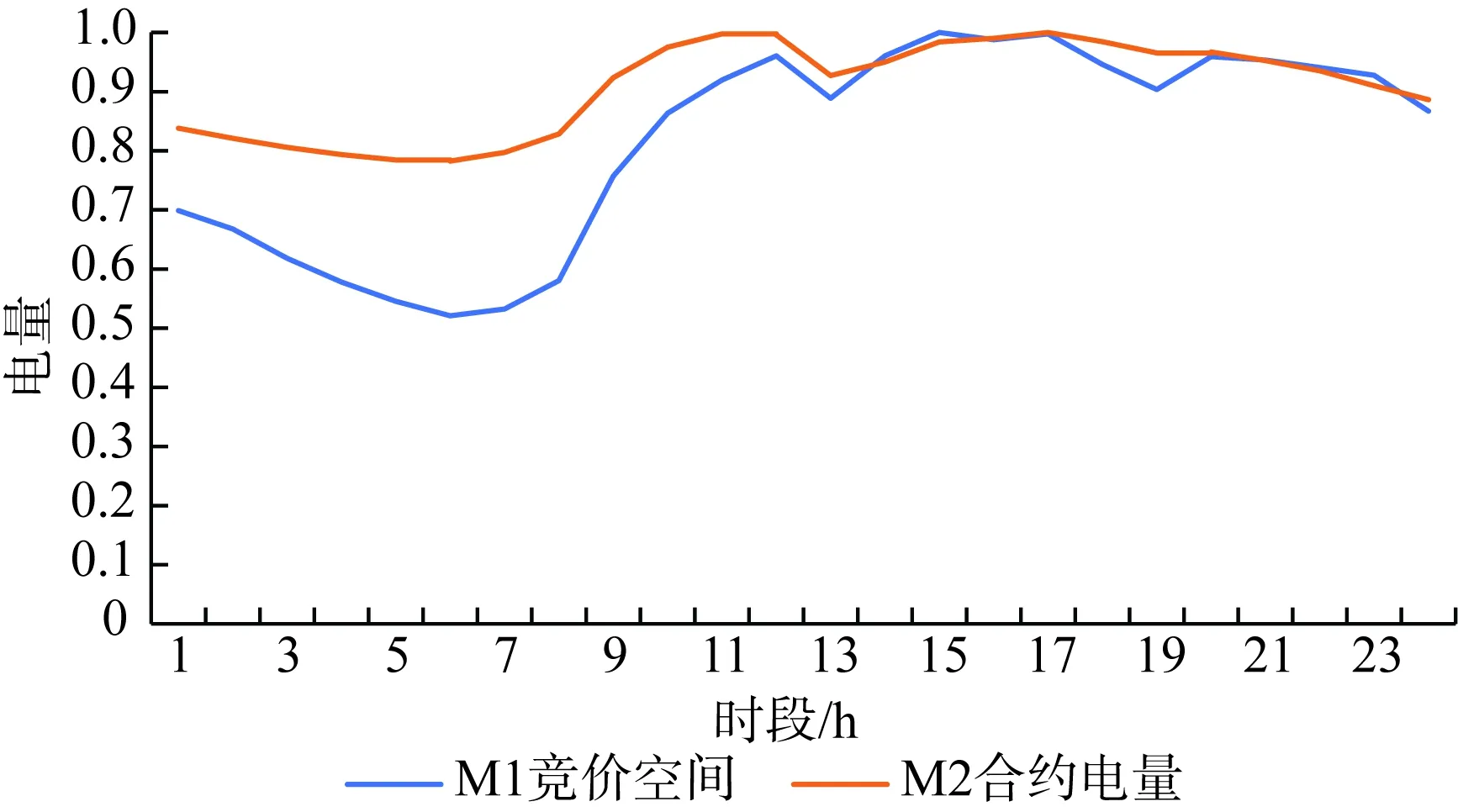
圖5 M1—M2電量分解曲線(歸一化后)Fig.5 Power decomposition curve of M1—M2(normalization)

各場景風險評估指標如表2所示，各指標排序如圖6所示。可以發現根據使用場景的不同，風險評估指標給出了不同的模型推薦：場景1下系統運營商關注誤差交易電量更大且對高誤差給予更多懲罰，采用相似日法的M1預測模型各時段均存在一定誤差，但由于相似日與預測日電價波動趨勢相近，最大誤差較小，基于此風險指標評價M1模型為最優模型；場景2下發電商關心日前價格預測誤差對自身預期收益的影響，根據圖5可知該發電商在9—14時段合約電量最高，該時段內的預測誤差風險也最高，而M4模型在該時段內的預測誤差較小，基于此風險指標判斷M4模型對預期收益影響最小，為6.04萬元，比排序第2的M1少400元，因此該場景下M4模型為最優模型；場景3下售電商考慮通過策略性報量盈利，此時M1方法雖然在傳統指標下預測精度不佳，但其準確地反映了日前價格與實時價格的高低趨勢，在該角度下優于其他3種預測模型。

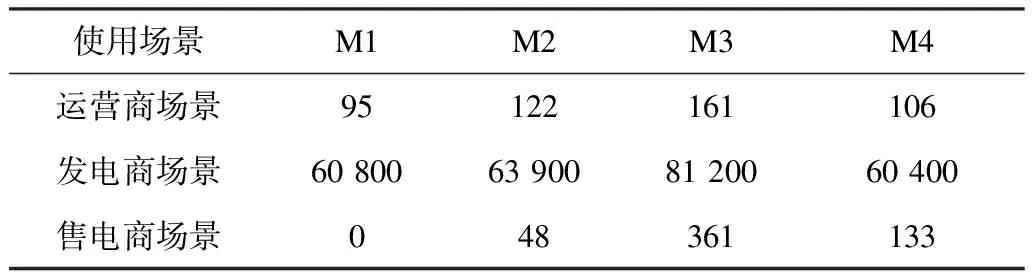
表2 風險評估指標結果Tab.2 Risk assessment indexes of different scenarios元

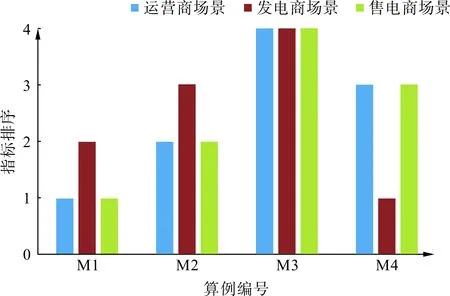
圖6 風險評估指標排序Fig.6 Rank of risk assessment indexes

上述仿真表明，風險評估指標針對每一種場景具有唯一的判斷結果，不會出現指標間存在歧義導致難以選取最優模型的情況。此外，風險評估指標能根據運營商及不同市場主體的決策特性及風險偏好，在各預測模型中選出最有利于其提升收益、降低風險的模型，該模型可能并不是傳統指標認為的預測誤差最小的模型。

3.4 工業用戶實際決策分析

為進一步說明本文所提指標能幫助市場主體獲取更高收益，本節考慮某工業用戶使用預測電價進行用電計劃安排，對比傳統指標及風險評估指標選出最佳模型的收益情況。假設某自來水廠需要按照用水需求向城市供水，自來水廠擁有蓄水池，也可以使用電動水泵抽取地下水，其優化空間為在電價較低時使用水泵蓄水，電價較高時從蓄水池放水。自來水廠決策模型為制定使購電成本最少的水泵運行計劃，同時滿足用水需求和蓄水池水位約束，具體如式(18)所示。

(18)

式中：ui,t為水泵i在t時刻的開關狀態，ui,t∈{0,1}；I為水泵數量；Pmax,i為水泵i最大運行功率；ht為蓄水池t時刻水位；Dw,t為t時刻用水需求；A為蓄水池表面積；Qmax,i為水泵i每小時抽水量；hini、hmin、hmax分別為初始水位、水位下限、水位上限。具體參數取值及水量需求數據取自文獻[25]。該優化問題為MILP問題，本文使用Cplex求解。

分別使用8月31日日前電價真值及模型M1—M4預測值，求解自來水廠水泵運行計劃，如附錄圖A2所示。將水泵運行計劃帶入日前電價真值得到使用不同預測模型的真實購電成本，如式(19)所示。

(19)

之后使用式(17)計算風險評估指標，設置權重為水泵運行功率。購電成本與風險指標值的數值如表3所示，不同預測模型的排序如圖7所示。可以看到采用電價真值作為決策模型輸入，理論購電成本是為2 775.15元，是所有算例中最低的，此時風險指標值為0，也是所有算例最低的。若采用預測電價替代真實電價作為決策模型參數，自來水廠制定的用電計劃將偏離最優點，導致購電成本提高。在4種模型中，使用M1產生的購電成本最低，較理論成本偏高2.32%，風險評估指標也給出了同樣的判斷結果，若采用傳統指標投票原則選出的誤差最小模型M2，其購電成本將較理論成本高4.16%。從圖7排序對比中可以看到，風險指標排序與實際購電成本排序完全相同，說明該風險評估指標能輔助用戶選擇更合適的電價預測模型。

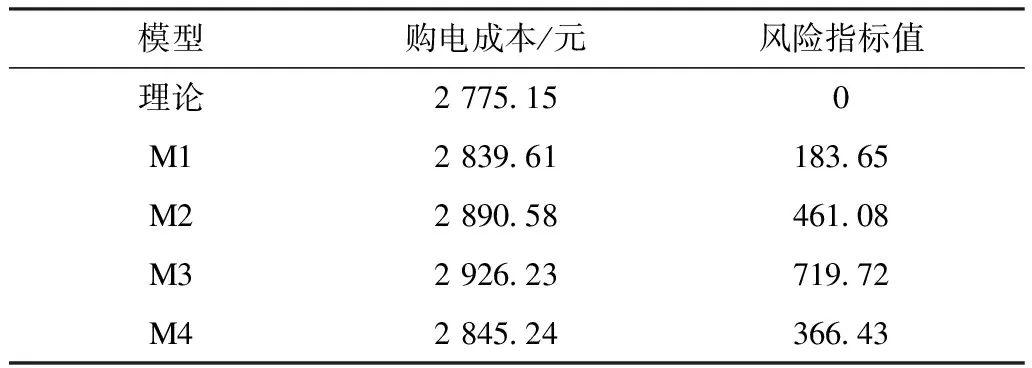
表3 各模型購電成本及風險指標Tab.3 Costs and risk assessment indexs of different models

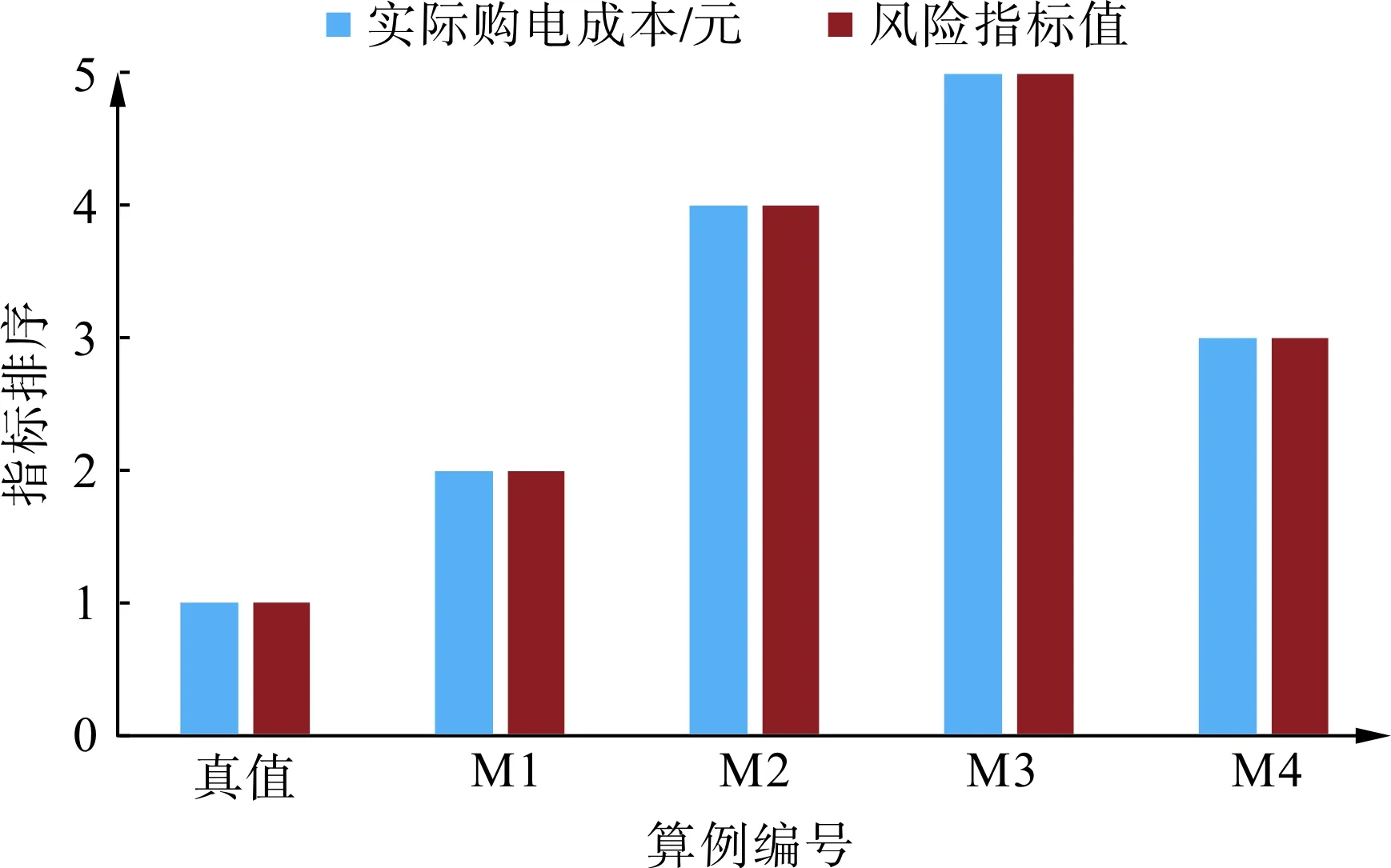
圖7 購電成本風險評估指標排序Fig.7 Rank of assessment index and cost of electric power purchase

5 結論

在價格波動頻繁、市場供需及參與者行為不確定性較高的現貨市場中，準確的價格預測難度較大，不同預測模型由于數據或模型層面的局限性必然存在一定誤差。傳統預測模型誤差評估指標可能出現多個指標排序結果不一致導致難以準確評價模型優劣，本文提出的風險評估指標可以根據預測主體的實際需求設置指標，具有反映主體誤差風險成本、判斷結果唯一等優點。在實際應用中，系統運營商可以將本文所提指標運用于事前風險評估體系中，通過選取更適合的價格預測模型降低由于預測不準導致的市場風險。除此之外，市場主體也可參考本文風險指標原則設計符合自身利益的評價指標，從而選取更適合的價格預測模型為參與市場博弈提供保障。算例結果表明工業用戶使用本文所提方法后，購電成本下降1.76%～2.97%。