纖維增強復材C 形圓臺殼件固化變形的預測方法

陶裕梅,鄭子君,邵家儒

（重慶理工大學 機械工程學院,重慶 400054）

復合材料因其較高的比強度，在航空、車輛、船舶領域的應用越來越廣泛。熱壓罐工藝是纖維增強復合材料的一種常見成形工藝，溫度、壓力場均勻可控，可同時處理多個模具，具有成形質量好、效率高的優勢。

纖維增強復合材料的固化是非常復雜的物理化學過程，由于材料化學收縮、熱變形、模具坯料相互作用等因素，脫模后工件必定會產生和模具形狀的偏差，即固化變形。預估固化變形的趨勢和大小，對優化工藝設計、提高制造質量有著重要的意義。在實驗研究方面，肖光明等在大量C 形和L 形工件的固化實驗的基礎上，建立了變形量的響應面[1]。王雪明等對大量曲面構件曲率與成型缺陷的統計分析發現，分層等拐角缺陷與曲率半徑成負相關[2]。王乾等通過實驗研究了纖維含量、富樹脂厚度對V 型零件成形回彈的影響，并建立了回彈預測有限元模型[3]。李桂洋等通過實驗驗證了經過優化成形溫度和壓力等工藝參數可提高制件內部質量和承載能力[4]。胡海曉通過預埋光纖布拉格光柵（fiber Bragg grating，FBG）傳感器，選取層板、L 型和C 型試樣，追蹤固化過程中的固化度和模量變化[5]。數值模擬方面，鄒堯等考慮了化學收縮和熱應變對長桁類復合材料零件固化變形的影響，并提出型面補償方法，將成形誤差降低到4%以內[6]。朱海華等采用熱結構耦合分析的方式模擬了固化過程，研究熱導率各向異性對溫度分布的影響[7]。董豐路等考慮了熱載荷下復合材料桿件的固化變形，提出桿件截面設計應具有對稱性以避免過度彎曲[8]。Bellini 等采用線彈性模型計算了不同鋪層順序下，熱變形導致的層合板翹曲[9]。Johnston 等指出固化過程中樹脂力學性質與固化度和溫度有關，提出了CHILE 本構模型[10]。梁群等采用CHILE 模型計算了大尺寸殼體的變形梁，并估算得出殘余應力可達兆帕級[11]。Ersoy 等根據固化變形時間相關性不明顯的現象，提出了屬性躍變的path-dependent 模型[12]，Ding 等在此基礎上進行了改進[13]。黃尚洪等結合了熱化學模型和黏彈性本構關系對固化過程進行模擬，并與光纖光柵傳感器的檢測結果進行了對比驗證[14]。有學者還對比了樹脂固化模擬中，線彈性、黏彈性、CHILE 模型和path-dependent 模型等本構模型的適用性，表明黏彈性模型的計算結果最好，但相應的參數測定和建模難度增加[13,15-16]。Jiao 等對近年來固化變形機理、模擬方案和控制方法上的認識進行了總結[17]。

研究表明，導致固化變形的應力大部分是在玻璃化后降溫階段產生的熱應力[18]。在變形預測的理論研究方面，常采用熱彈性力學模型來推導典型形狀的熱致固化變形量理論解。由于層合平板和C 形圓殼的幾何簡單，工程中常見的L 形和U 形等工件可以視為兩者的組合。Kim 等[19]和Abouhamzeh等[20]分別推導了層合板在固化后的翹曲變形。Radford 等提出了C 形圓殼的熱回彈角度預測公式[21-22]。Radford 等得到的公式基于彈性本構且只考慮殘余正應力，Wisnom 等[23]和Ersoy 等引入了剪切應力和材料相變的影響[12]。Ding 采用廣義平面應變模型，進一步考慮了面外應力的影響[24]。上述理論研究文獻考慮了常見定截面L 形、U 形和C 形零件，預測效果良好，但實際生產中截面漸變的工件更常見，以小型固定翼飛機為例，機翼前緣圓弧、機頭罩、機身后部覆蓋件等均可以看作是截面漸變的C 形工件。這類工件的固化變形主要借助有限元軟件進行數值分析，并往往需要開發自定義材料庫，實現較為繁瑣。

C 形圓臺殼件可以認為是C 形圓殼件的推廣，其沿母線方向上，截面半徑線性改變，常可作為寬度漸變結構的覆蓋件，使用范圍比后者更廣。在設計初期若能對此類工件的固化變形量有合理估計，對通用航空領域提高制造精度、縮短工藝開發周期有著重要的意義。本工作研究纖維增強復合材料C 形圓臺殼件的固化變形規律，以得到能快速預測此類零件變形量的方法。

1 C 形圓臺殼固化變形量理論分析

1.1 理論公式推導

圖1 為纖維增強復合材料的典型熱壓罐固化工藝曲線。由圖1 可見，在固化度X低于凝膠點固化度Xc之前，復合材料的樹脂基體處于黏流態，不能形成明顯的殘余應力；在凝膠點和玻璃化點之間，材料處于橡膠態，彈性模量較小，但能夠因化學收縮和熱膨脹在內部產生一定的應力；隨著固化進行，材料彈性模量逐漸增大，當玻璃溫度Tg高于工藝溫度時，材料完全玻璃化，模量達到最大，在此階段構件內部能夠產生明顯的應力。因此導致固化變形的應力大部分是在玻璃化后降溫階段產生的熱應力[18]。

圖1 固化溫度工藝曲線以及固化參數隨時間的變化Fig.1 Curing temperature process curves and changes of curing parameters over time

基于上述論斷，對于C 形圓殼（圖2（a）），Radford等提出了經典的熱回彈角度預測公式[21]：

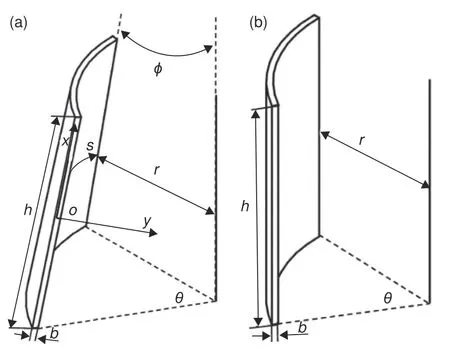
圖2 兩種C 形構件模型示意圖（a）圓殼模型；（b）圓臺殼模型Fig.2 Schematic diagrams of two C-shaped component models（a）round shell model；（b）round pedestal shell model

式中：ατ、αn分別是C 形圓殼模型環向和法向的熱膨脹系數；θ為圓心角（見圖2（a））。

文獻[22]認為，固化反應導致的化學收縮也服從相同的機制，于是式（1）可以改寫為：

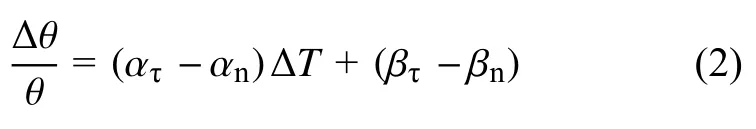
式中：βτ、βn分別是C 形圓殼模型環向和法向的化學收縮應變。

由于式(1) 和式(2) 高度的簡潔性，至今仍然是估算C 形圓殼角度變形最重要的“拇指法則”。

本工作推導式（1）、（2）的更一般情形，即半徑隨母線長度變化時的情形。此時模型可稱為C 形圓臺殼，如圖2(b) 所示。建立正交坐標系，x、y、s軸分別沿著母線、厚度和水平截面內弧長方向。參考文獻[20，22]，對C 形圓臺殼件的固化變形做如下假設：（1）變形主要源于降溫階段的熱變形，此階段工件變形是線彈性的；（2）殼體是沿各方向均勻鋪層的復合材料，宏觀上是橫觀各向同性（transversely isotropic）的；（3）頂底半徑差和厚度相對于圓臺半高處半徑而言是小量，變形量相對于原始尺寸是小量；（4）工件變形前后均為C 形圓臺殼，且各材料點在xy截面內的應變狀態相同；（5）忽略剪切變形的影響。

顯然，此類工件的幾何形狀可以用5 個參數描述，即半高處半徑γ、半頂角?、母線長度h、厚度b以及圓心角θ。根據假設4，描述固化變形只需給出這5 個參數的相對變化，這里采用虛功原理推導。

由假設4，工件厚向和母線方向的應變分別為：

又在xy平面上歸一化坐標為(x,y)的環向纖維(其中x,y∈(?0.5,0.5))，原始長度為：

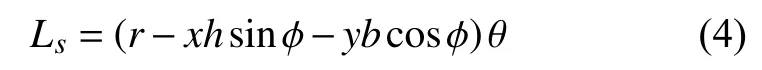
利用全微分公式，可得變形后的環向應變為：

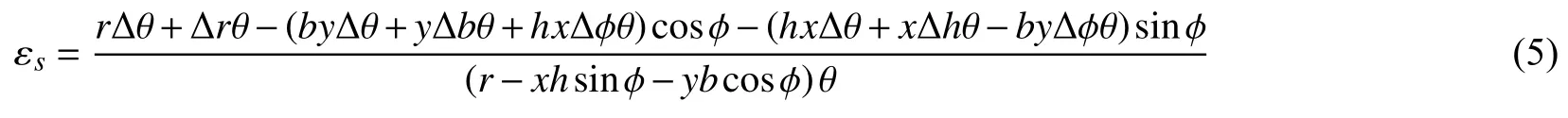
本問題中總應變由熱變形以及應力造成，在忽略泊松比的影響時有：

式中：Eτ、En分別是橫觀各向同性材料中橫向和法向的楊氏模量。由式(6) 可以解得正應力分量 σx、σy、σx。另一方面，虛應變分量δεx、δεy、δεs可通過在式（3）、（5）中用虛增量δb、δh、δr、δθ、δ?代替參數增量?b、?h、?r、?θ、??得到：

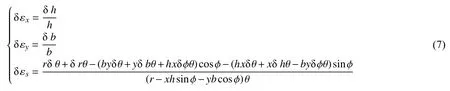
由假設5 不考慮切應變分量。于是內力虛功為：

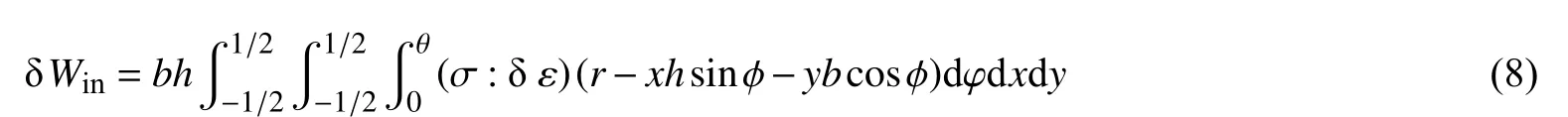
由式(5)可見式(8)被積函數的分母中出現了變量x,y，不利于積分。根據假設3，hsin? ?r,b?r，在計算環向應力 σs時，可以將式(5)的分母部分替換為其一階近似：

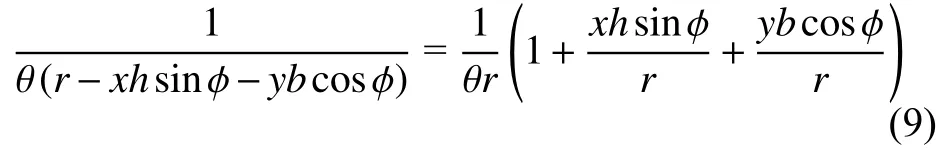
此時式(8)的被積函數已是x,y的多項式，積分得到簡化。可以算得：

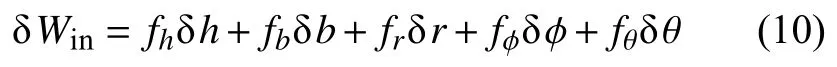
其中：

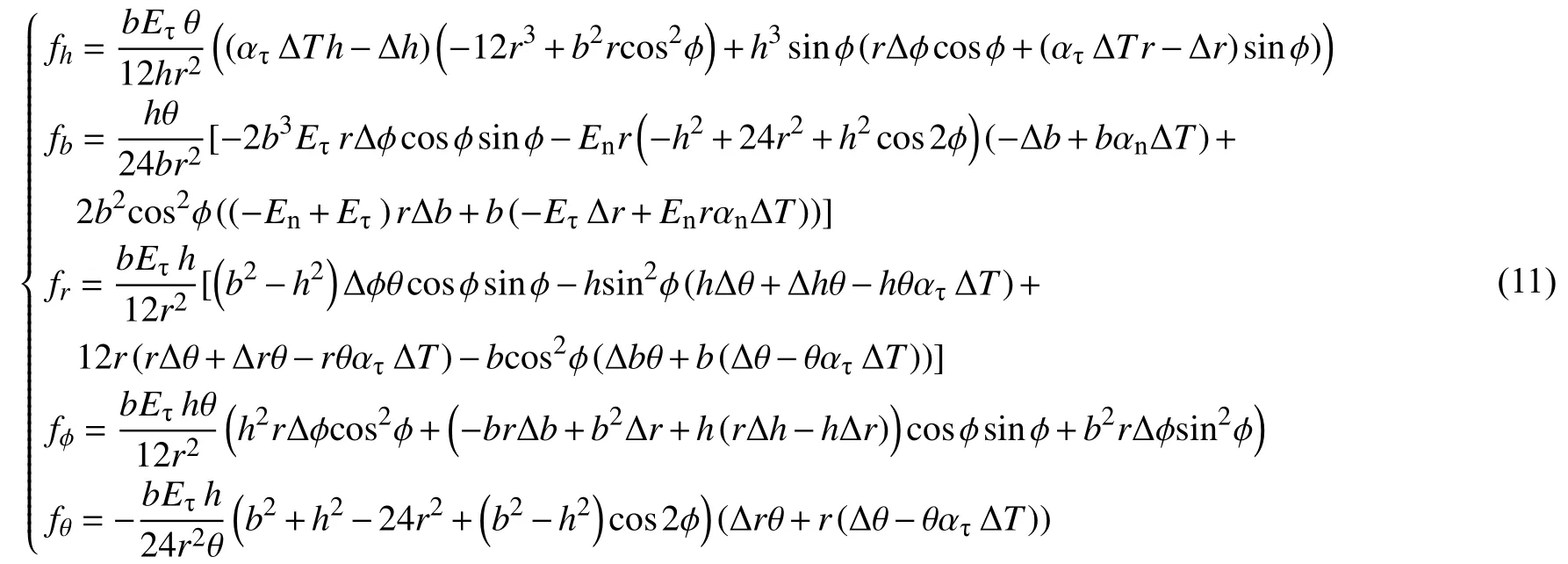
根據虛功原理，內力虛功δWin等于外力虛功δWex。本問題中只考慮熱應變導致的變形，因此外力虛功為零。對比式(10)中各虛增量的系數，可以得到式(11)中的5 個式子均為零。求解該代數方程組即得：

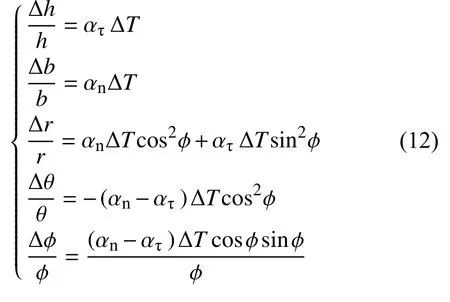
可以看到式(12)的結果并不包含材料的彈性參數。特別指出：雖然在式(6)中假設了泊松比為零，但這僅僅是本工作為了式(11)的簡潔性而進行的簡化。如果在式(6)中考慮泊松比，式(11)將非常復雜，但是最終得到的結果仍然是式(12)，即固化變形量也不包含彈性參數的影響。

當?=0時，工件退化為了C 形圓殼件，此時的式(12)指出半頂角不再改變，母線、半徑和厚度的相對變化量分別為對應方向的熱應變值，而圓弧角度回彈量即為式(1)。因此C 形圓殼件的固化預測式可以視作本工作公式的特殊情形。當需要進一步考慮化學收縮應變的影響時，也可模仿式(2)修改預測公式：

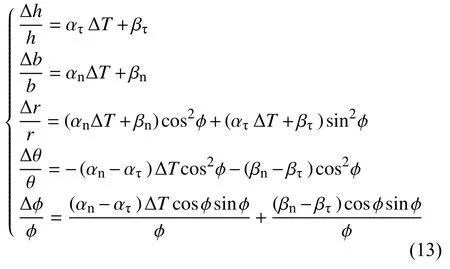
在纖維增強復合材料固化過程的升溫階段，樹脂處于黏流態或橡膠態，模量較小，不易形成較大的殘余應力，對固化變形的影響很小；而在保溫—降溫階段，化學應變和熱應變均是收縮的，且法向由于缺乏纖維的支持，變形量大于橫向，即整體上有βτ<βn<0,ατ?T<αn?T<0。代入式(13)可知，固化后C 形圓臺殼工件的母線縮短、厚度變小、半徑變小、半頂角減小、而圓心角增大。

1.2 模擬正交實驗驗證

由式(12)、(13) 可知，C 形圓臺殼的固化變形量與多個幾何參數有關。為驗證本理論計算的合理性，采用有限元方法對C 形圓臺殼件的熱致固化變形進行正交模擬實驗（圖3）。注意到模型尺寸的等比例放縮不會影響結果，可固定殼厚為1 mm，從而只需考慮4 個變量：圓臺半高處半徑r、半頂角?、母線長度h以及圓心角θ。采用四變量三水平正交實驗設計，參數取值如表1。復合材料類型為玻璃纖維增強樹脂，采用的正交織物材料可視為橫觀各向同性的，其等效材料參數如表2[25]。根據此類復合材料的典型工藝曲線（圖1），取整個固化降溫階段的總溫差為107 ℃。

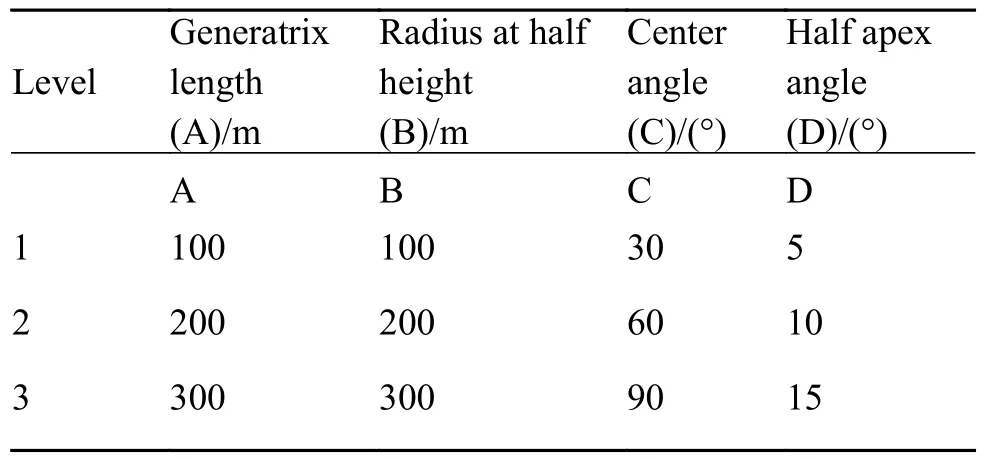
表1 正交實驗變量及對應水平選擇Table 1 Orthogonal test variables and corresponding level selections

表2 玻璃纖維增強樹脂基復合材料（Hexcel7781/LY5052/ HY5052,Vf=0.49）的等效力學性能Table 2 Equivalent mechanical properties of glass fiber reinforced resin-based composite material（Hexcel7781/LY5052/HY5052,Vf=0.49）

圖3 C 形圓臺殼的1/2 有限元模型Fig.3 Symmetrical finite element model of C-shaped circular pedestal shell

根據對稱性，建立圓臺殼的1/2 對稱模型，并采用六面體實體單元，結構化網格剖分。在對稱面上額外施加簡支撐。旋轉單元坐標系使之與圖2(b)中的xys坐標系重合。對結構施加均勻溫度載荷，進行考慮幾何非線性的彈性計算。

計算完成后取6 個關鍵點（圖3），折算有限元模擬的工件幾何參數改變量，計算結果與預測公式(12)對比，結果如圖4 所示。可以看出，在不同幾何參數組合和相當大的參數范圍內，理論解和數值解基本吻合，由圖4 還可以看到，有限元計算的變形量總是略大于本工作計算結果，這是因為本工作對工件變形后仍為圓臺面的假定增加了結構的剛性。由于半頂角的增量 ??的絕對值較小，且由多個幾何參數間接計算得到，與有限元模擬的差距最大。從正交實驗還可以看出，當圓心角和半徑較大（因素C、B 取水平3）時，對變形模式的假設與真實情況偏差越大，誤差更加明顯。

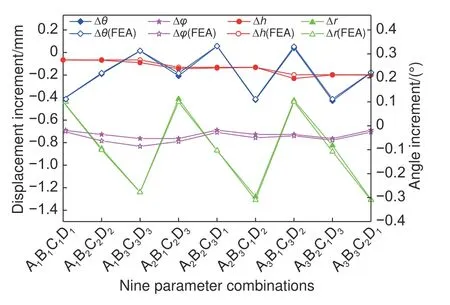
圖4 C 形圓臺殼件幾何參數變量的公式預測結果與有限元對比Fig.4 Comparison of formula prediction results of geometric parameter variables of C-shaped circular truncated shell and finite element

總體而言，本工作提出的理論解與有限元模擬結果吻合良好，表明了其在預測C 形圓臺殼件熱致固化變形時的正確性和適用性。

2 基于path-dependent 模型的固化模擬方案

前述討論考慮了熱壓罐固化工藝中已固化的復合材料由于降溫階段的溫差導致變形（圖1）。這是因為鋪層較厚時，玻璃化前的材料模量較低，其化學收縮和熱應變不會形成較大的應力；然而文獻表明，當鋪層較薄時，工件在玻璃化前受到模具的約束較強，也能夠形成明顯的應力，從而影響固化變形[12]。若要進一步考慮玻璃化前橡膠態階段的化學-熱變形的影響，可以基于path-dependent 本構模型進行有限元模擬[13-15]。如圖5 所示，該模型常忽略材料在黏流態的彈性模量，而認為在橡膠態和玻璃態時的切線彈性模量分別為常數；當前溫度T低于玻璃化溫度Tg時，材料立即玻璃化，切線模量發生突變，但應力仍連續變化，該本構關系的增量表達式為：

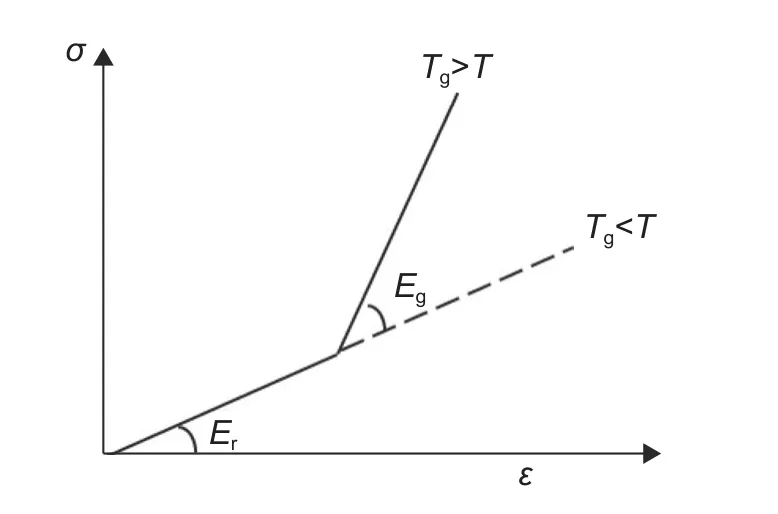
圖5 path-dependent 本構模型示意圖Fig.5 Schematic diagram of path-dependent constitutive model

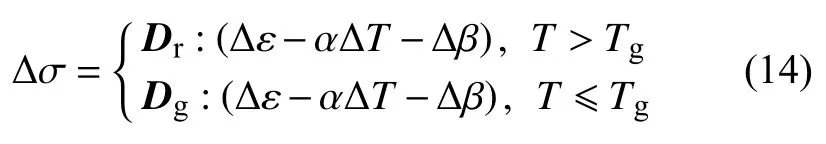
式中：Dr,Dg分別為橡膠態和玻璃態下復合材料的四階彈性張量。

通常基于有限元軟件二次開發自定義材料的方式來實現上述本構模型[12-13]，增大了建模分析的難度。這里通過將固化度場與力學場解耦，使用帶初應力的熱彈性分析來等效實現path-dependent 模型。

當復合材料鋪層較少時，可以忽略溫度梯度，假設整個工件內的溫度分布均勻。這在傳熱學上稱為集總熱容法，其適用條件為畢渥數Bi滿足：

式中：hf是對流換熱系數；λ是固體的導熱系數；δ0是固體中心到表面的特征長度，這里取復合材料厚度的一半。例如按熱壓罐內對流換熱系數h=85.2 W/(m2?K)[26]，玻纖復合材料的平均導熱系數0.6 W/(m?K)估算[27]，則當鋪層厚度低于1.4 mm時，采用上述假設是合理的。

由于固化度的變化率只是當前固化度X和溫度T的函數[28]：

可知工件各處固化的程度相同。根據DiBenedetto 公式[27]，玻璃化溫度只與固化度有關：

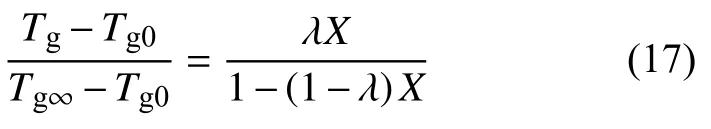
式中：Tg0,Tg∞分別是尚未固化和完全固化后的玻璃化溫度，與 λ一樣是材料常數。由式(17) 易知，工件各處將同時玻璃化，因此有限元模擬時可以根據復合材料所處的狀態分步處理，流程如下：

首先，在給定工藝溫度曲線T(t)后，利用式(16)、(17)求解固化度和玻璃化溫度曲線，找到凝膠點(XC=X0)和玻璃化點(T=Tg)，如圖1 所示；

其次，將工件一面固定在模具上，施加從凝膠點到玻璃化點之間由于升溫和固化導致的本征應變，并在自由面施加熱壓罐內壓力，使用橡膠態的彈性參數計算變形和應力（表1 和表2）；

再次，以初始應力和初始缺陷的形式繼承橡膠態階段的應力和變形，進一步施加從玻璃化點到工藝結束由于降溫和固化導致的本征應變，改用玻璃態的彈性參數計算變形和應力；

最后，移除模具的約束，使用玻璃態的彈性參數計算回彈量和殘余應力。

上述模擬方案避免了引入自定義材料二次開發，更加容易實施，并且當忽略固化度和溫度在工件內的空間梯度時，與常用的path-dependent 本構模型[12-13,15]是完全等效的。

為驗證本工作提出的簡化模擬方案的可行性以及計算效率上的優勢，建立文獻[12-13]中C 形模型的固化變形分析，并與實驗測量的結果進行對比（圖6）。結果表明，本工作提出的簡化方案的回彈角與文獻和實驗測量值吻合良好。其中厚度為3 mm 的C 形圓殼的計算時間與文獻[13]對比如表3 所示。由于本工作的簡化實現方案避免了使用非線性自定義材料，在網格數同為2400，時間步數同為218 步的情況下，相比原始path-dependent方案減少時間代價約80%。

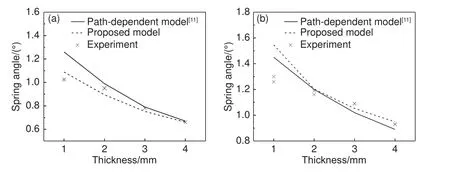
圖6 C 型構件回彈預測結果與實驗、文獻對比（a）（90）n（n=4、8、12、16）；（b）（90/0）ns（n=1、2、3、4）Fig.6 Comparison of spring-in prediction results of C-shaped model with experiments and literatures（a）（90）n（n=4,8,12,16）;（b）（90/0）ns（n=1,2,3,4）

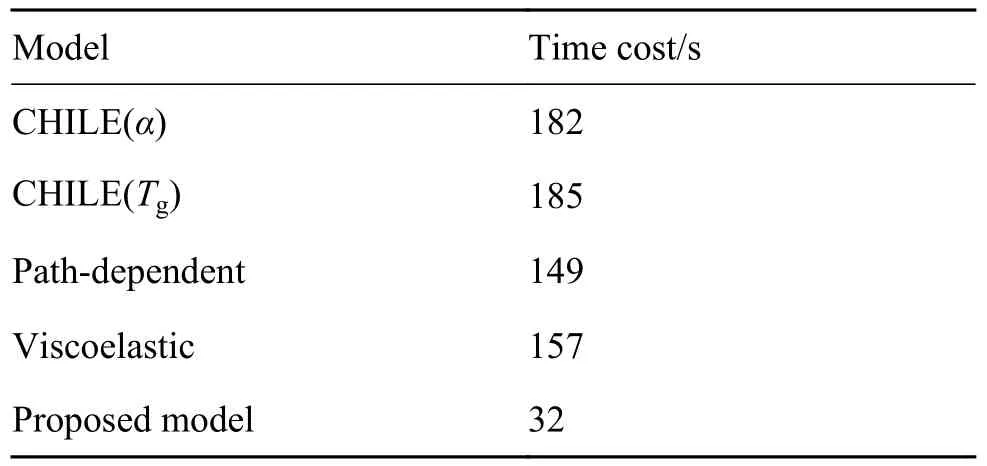
表3 3 mm 厚C 形模型的不同本構模型運行時間對比Table 3 Comparison of time costs of different constitutive laws for C-section with 3 mm thickness

3 工程案例與實驗

某小型固定翼飛機的機頭罩安裝后存在明顯的縫隙，為驗證本工作提出的公式和有限元模擬方案的可行性，對機頭罩進行成型預測及裝配約束的變形分析。圖7 為機頭罩模型，模型長775 mm，截面近似為C 形圓槽，截面尺寸沿長度方向逐漸變化，前端槽寬900 mm，后端寬1125 mm，可以近似為C 形圓臺殼模型。零件采用玻璃纖維環氧織物復合材料LY5052/7781，性能參數如表2，單層正交織物預浸料厚0.25 mm，鋪層方案為[45?/0?/?45?/90/40?]，其中0°纖維方向為垂直于機頭罩橫軸線方向。成形時熱壓罐內壓力為0.7 MPa，溫度工藝曲線如圖1 所示。在常溫下脫模完畢后，將零件對稱軸緊靠在模具上，此時零件側沿與模具間有明顯的間隙。取側沿上的三點（如圖8 所示），采用游標卡尺測量了水平位移量。再分別通過熱彈性有限元模型、本工作簡化的path-dependent 模型以及本工作理論預測公式對機頭罩的固化變形量進行估算，并與實際測量結果進行對比。

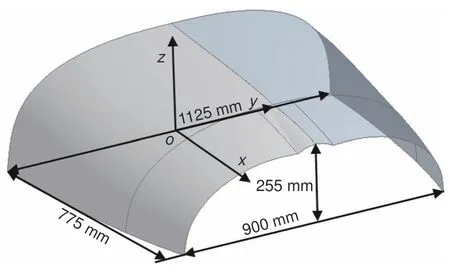
圖7 某小型固定翼飛機機頭罩幾何模型Fig.7 Geometric model of nose cover of a small fixed-wing aircraft

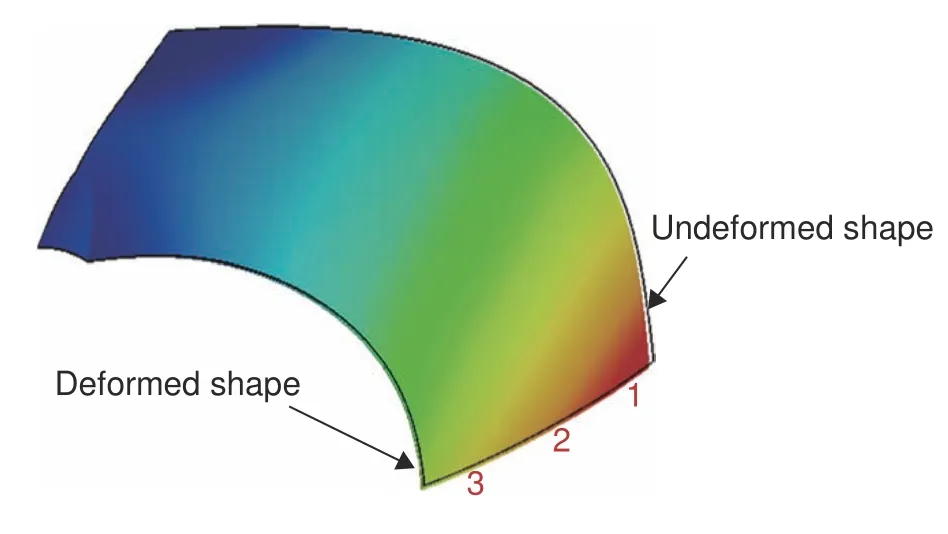
圖8 機頭罩1/2 模型固化變形云圖及實驗測量點Fig.8 Curing deformation contour and experimental measurement points of symmetrical model of nose cover

由于結構的對稱性，有限元分析時只取右半部分。根據固化溫度工藝曲線，求解玻璃化轉變溫度Tg以及固化度X隨時間的變化如圖1 所示。取XC=0.5[28]，可算得橡膠階段和玻璃階段的固化溫差分別為?Tr=?10oC,?Tg=?97oC。基于熱彈性模型的有限元模擬采用玻璃態彈性參數，將橡膠態和玻璃態下的溫度應變和化學收縮之和作為本征應變施加；基于path-dependent 本構模型的有限元模擬方案則如前所述。為了移除剛體位移，回彈階段在對稱軸的兩端施加簡支撐。

采用理論解公式進行預測時，由于機頭罩模型的截面并非標準的C 形圓弧，將模型用兩個頂角相同、并排相切的圓臺殼來擬合，擬合參數如表4。再采用式（12）或式（13）分別計算兩段圓殼的變形量，拼接后得到整體的變形。最后用模具形狀疊加上變形量得到零件的最終形狀。

表4 機頭罩簡化幾何模型參數Table 4 Simplified geometric model parameters of nose cover

4 結果分析與討論

在各預測變形模型中提取側沿的最終形狀，并將側沿在xy平面上的坐標與實驗結果進行對比，結果如圖9 所示。由圖9 可以看到，各種模型預測的機頭罩變形形式相近，都表明輪廓將內移，變形量沿x正方向逐漸減小的特點，理論解模型、熱彈性模型和path-dependent 模型預測的機頭罩半跨長平均縮小量分別是8.1 mm、7.6 mm、6.1 mm，均與實測值7.7 mm 基本接近。總體而言，基于pathdependent 模型的有限元解考慮了相變導致的力學性質改變，實現復雜度相對較高，但只在測量點1 明顯優于其他解。基于熱彈性模型的有限元解未考慮橡膠態與玻璃態的力學性質差異，高估了固化時的殘余應力，變形量更大。理論解式(13)與熱彈性模型基于相同的假設，因此兩者的結果非常相近，在模型前端的差異主要是因為工件并非標準的圓臺殼。而理論解式(12)沒有考慮橡膠態階段化學收縮對固化變形的影響，這在鋪層較少的情況下將明顯低估變形量[12]。

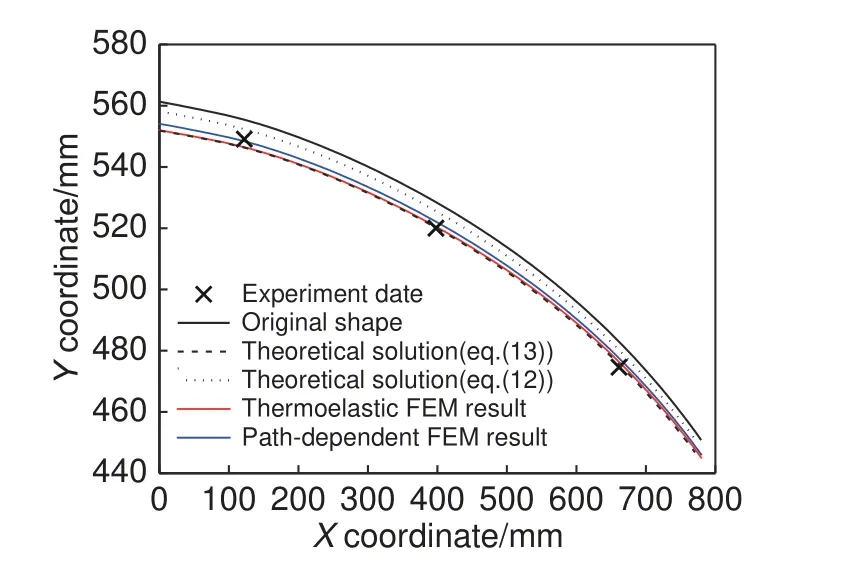
圖9 不同變形輪廓與實驗測量結果的對比Fig.9 Comparison of different deformation profiles with experimental measurement results

殼罩類零件起到保護內部控制系統和電器裝置，維持飛機整體的空氣動力學外形的作用，其外觀形狀非常重要。為進一步研究固化變形對殼罩裝配后形狀的影響，模擬裝配過程，提取用pathdependent 模型算出的已有固化變形的零件，將其對稱軸與側沿固定在原設計位置處，此時的零件形狀與原設計曲線對比如圖10 所示。

由圖10 可以看出，在此種約束下機頭罩模型的構型與設計曲面有一定的偏差。圖中標記處為鉚釘布置位置，可見AB 段在設計曲面下方，而BC 段在設計曲面上方。實際裝配完成后的照片如圖11 所示。考慮到與機頭罩鉚接的發動機罩是較矮的穹頂形，固化變形較小，其輪廓可以作為原始設計的參照。可以看到機頭罩的AB 段確實略低于發動機罩，而BC 段明顯更高，兩者間有明顯的縫隙。這從側面驗證了本工作有限元模擬方案的正確性，也說明復合材料的固化變形對裝配后的飛機外觀有著明顯的影響。

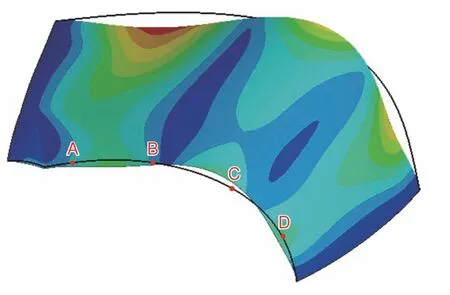
圖10 機頭罩1/2 模型裝配對稱軸與側沿后的變形云圖Fig.10 Deformation contour of half of nose cover model after assembling symmetry axis and side edges

圖11 某小型固定翼飛機機頭罩安裝后照片Fig.11 Photo of a small fixed-wing aircraft after the installation of the hood

5 結論

（1）采用虛功原理推導出C 形圓臺殼熱致固化變形的理論預測公式。公式表明：固化后C 形圓臺殼工件的母線變短、厚度變小、半徑變小、半頂角減小、圓心角增大。

（2）為驗證提出公式在各幾何模型參數組合下的適用性，選擇4 個關鍵變量進行三水平的正交實驗，并建立相應的有限元模型進行對比，兩種方法的計算結果一致性較好，表明公式可以用于初步估計復合材料的固化變形量。

（3）對于鋪層厚度較小的復合材料，提出基于path-dependent 模型的簡化模擬方案，相比原始path-dependent 模型實現更簡單，計算時間可減少約80%。以近似C 形圓臺殼的某飛機機頭罩為例，分別采用本工作公式、熱彈性有限元模型、簡化的path-dependent 模型進行固化變形模擬，均與實測變形量基本吻合。

（4）采用有限元方法模擬了零件固化變形對裝配后最終形狀的影響，模擬結果能夠解釋實際制造中發現的裝配縫隙，這可能對飛機的氣動特性造成影響，因此分析復合材料固化變形是非常必要的。