濕-熱-機耦合梯度多孔材料梁的非線性力學行為
李清祿,王思瑤,張靖華
(蘭州理工大學 理學院,蘭州 730050)
多孔材料是一種兼具功能和結構雙重屬性的工程材料,其綜合性能優異,可應用于航空、航天、航海等諸多領域[1-2]。為適應航空、航天、航海等在輕量化、多功能、高強度等方面的需要,制造了集功能梯度材料和多孔材料兩者特點于一身的新型工程材料——梯度多孔材料。梯度多孔材料是一類輕質材料,其材料性能的變化是連續的,即這些性能隨結構一個或多個方向的位置變化而變化,以達到所需的目的。梯度多孔材料結構由于其獨特的優點,在航空、航天、海洋等領域得到廣泛的應用。近二十年來,由于梯度多孔材料的應用,使得人們對這些材料力學行為進行了大量的研究[3-5]。飛機起飛后進入大氣層,跟大氣層的摩擦溫度會急劇增加,另外會遇到雷雨等極端濕度環境,其濕-熱環境下的力學行為是科技工作者關注的問題。從工程實際考慮,機械結構的很多連接部分在力學角度都簡化為鉸接,因此研究簡支梁的力學行為更符合工程實際問題。
多孔梯度材料的研究主要集中在材料的制備方面。楊保軍等[6]對梯度多孔金屬材料制備工藝和研究應用概況做了詳細報道。李元偉等[7]介紹納米多孔金屬材料的幾種制備方法,指出其應用及其力學性能的研究現狀。郭亞周等[8]研究閉孔泡沫金屬的單軸壓縮性能,基于 LS-DYNA 軟件分析閉孔泡沫金屬壓縮力學性能。劉培生等[9-11]運用自行提出的“八面體模型”,比較全面地研究網狀泡沫金屬的系列力學性能,包括拉伸強度、彈性模量、雙向拉伸、多向拉壓、疲勞指標及其彎曲、扭轉、剪切等方面。梁結構是工程中常見的結構之一,因此有必要對梯度多孔梁在機械或其他環境下的力學行為進行研究。
Magnucki 等[12]利用總勢能的穩態原理,計算軸向受壓多孔梁的臨界屈曲荷載,并給出了兩種孔隙率分布多孔材料。Jasion 等[13]對三層泡沫夾芯梁進行分析、數值和實驗研究,比較不同方法得到的臨界屈曲荷載值。Chen 等[14]采用Ritz 方法研究功能梯度多孔Timoshenko 梁的屈曲和靜態彎曲行為。李麗等[15]基于多孔介質理論,分析大撓度彈性梁在微觀不可壓飽和情況下的擬靜態響應解,但在研究中沒有考慮梁的軸線伸長。Navvab 等[16]對二維梯度多孔錐形Euler-Bernoulli 梁的屈曲行為進行詳盡的分析。
工程中存在一種隨結構的變形而方向發生變化的隨從力。例如,航空航天的火箭和噴氣式飛機均引起隨從力,這種非保守的隨從力將引起機翼的顫振。另外機箱儲油罐內液體的壓力也屬于這類力。因此研究這類載荷下的力學行為具有現實的工程背景。李清祿等[17]研究熱環境下非對稱FGM 梁受到隨從載荷的非線性力學響應,指出均勻和非均勻升溫對梁彎曲和屈曲行為有較大的影響。正如文獻[18]指出,梯度材料的力學性能是制約其應用的一個重要因素,梯度多孔結構力學行為的研究是目前國內外研究的熱點問題之一,但大都集中在綜述和制備方面。從文獻的調研來看,關于梯度多孔梁在外載荷下的力學行為的研究不多,而隨從載荷下的力學行為的文獻報道十分鮮見。
本研究精確考慮梁的軸線伸長,研究濕-熱-機(特指航空飛機上受到的隨從載荷)梯度多孔材料簡支梁的非線性力學行為,假設材料性質只沿材料厚度變化,考慮兩種孔隙率分布的梯度多孔梁,建立濕-熱-機多變量耦合梯度多孔材料簡支梁的大變形數學模型,采用打靶法將多變量耦合的控制微分方程進行數值求解,獲得簡支多孔梁的在濕/熱環境下彎曲或屈曲的平衡路徑曲線和平衡構形圖,分析對稱和非對稱模型下梁的非線性力學行為的不同。
1 梯度多孔材料梁
考慮處于濕熱環境中的梯度多孔材料梁,其長、寬、高分別為l×b×h。軸線方向為x軸,厚度方向為z軸,坐標原點置于梁左側且xoz位于幾何中面上。溫度T和濕度C沿厚度方向穩態分布,且梁上作用沿軸線均勻分布的隨從載荷q如圖1 所示。

圖1 梯度多孔簡支梁的變形示意圖Fig.1 Deformation diagram of gradient porous simply supported beam
1.1 梯度多孔材料
圖2 所示為兩種非均勻孔隙率分布或FG 孔隙率分布模型,分別是由Beam-Ⅰ和Beam-Ⅱ定義的模型。

圖2 兩種孔隙分布模式(a)對稱模型;(b)非對稱模型Fig.2 Two patterns of porosity distributions(a)symmetric model;(b)asymmetric model
假設多孔材料的力學性能沿厚度方向連續變化,材料屬性即楊氏模量E(z)、熱膨脹系數α(z)和濕膨脹系數β(z),如下式所示[14]:
Beam-Ⅰ為關于幾何中面對稱模型

Beam-Ⅱ為關于幾何中面不對稱模型

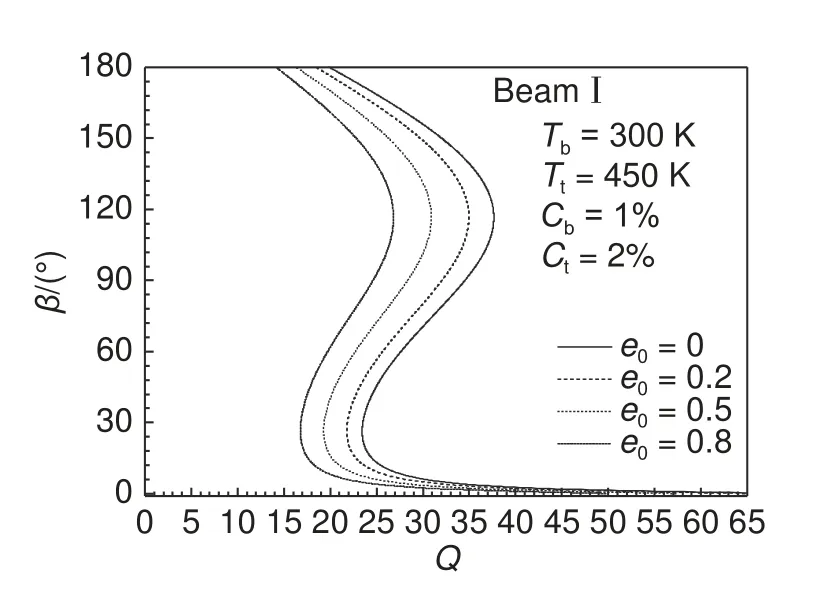
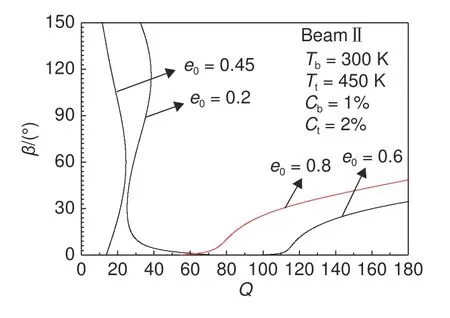
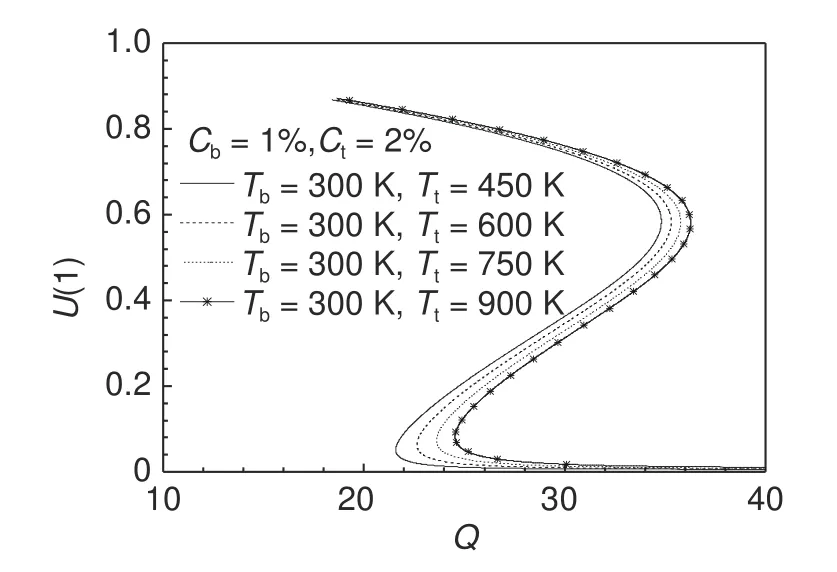
式中:e0為材料的孔隙率系數,e0=1?E2/E1(0 記上表面的溫度和濕度記為Tt和Ct,下表面的溫度和濕度記為Tb和Cb,Tr=Tt/Tb,Cr=Ct/Cb;且梁兩側溫度和濕度都均勻分布。 對于線性濕熱上升,溫度和濕度特性可寫為: 當多孔材料處于正弦濕熱上升時,溫度和濕度呈非線性變化: 取基礎溫度T0=300 K,濕度C0=0%(質量分數/%,下同)。 文獻[19]指出:對多孔材料,取非均勻線性變化的溫度和濕度場就能描述工程中濕熱帶來的影響。因此,本工作考慮只沿厚度方向呈線性變化的情況。 式中:彈性應變;溫度應變為εT=α(z)·(T?T0);濕度應變為εC=β(z)·(C?C0)。θ為梁變形后撓曲線的切線與x軸正向夾角;η為軸線伸長率。 結合文獻[17],[20] 可給出無量綱形式的非線性控制微分方程如下: 式中:S為梁軸線弧長;U和W分別為軸線上的點在x,z方向的位移;PH和PV代表橫截面內沿x,z方向的內力分量;M為彎矩。 上述方程的無量綱變換如下: 熱軸力和熱彎矩為: 濕軸力和濕彎矩為: 式中:τ=12δ2α1Tb,τ′=12δ2β1Cb。 對Beam Ⅰ模型: 對Beam Ⅱ模型: 相應的量綱一邊界條件為: 式中:β為梁的左端轉角。這樣,梯度多孔簡支梁在濕-熱-機(隨從載荷) 下的非線性力學問題就歸結為方程(12)~(14) 在邊界條件(26) 和(27)下的兩點邊值問題。 方程(12)~(14)是多變量相互耦合的強非線性方程組,只能通過數值方法求其數值解。常用的數值方法有插值法、利茲法、微分求積法等。而打靶法在求兩點邊值微分方程中具有不可比擬的優勢,計算結果不依賴于前面幾種方法需要依賴網格的劃分,計算耗時少且精度高,本研究采用打靶法進行數值模擬。其原理可參考文獻[21]的描述。 對鋼做成的開孔泡沫金屬梁,其E0=200 GPa,α1=1.2×10?5/K?1,β1=5×10?4。為了分析濕-熱條件下的多孔材料梁的力學行為與非濕-熱環境下有何不同,只考慮隨從載荷的情況下(T=0,C=0),繪制出了圖3 和圖4。 圖3 不同孔隙率下β-Q 的關系曲線(Beam Ⅰ)Fig.3 β vs Q for different porosity e0(Beam Ⅰ) 圖4 不同孔隙率下β-Q 的關系曲線(Beam Ⅱ)Fig.4 β vs Q for different porosity e0(Beam Ⅱ) 圖3 和圖4 給出了左端轉角隨載荷Q的變化情況。顯然,Beam I 模型下梯度多孔梁會發生屈曲失穩,而Beam II 模型梁則不會出現屈曲,而是在外力影響下產生彎曲變形。同時,圖3 中反映出孔隙率越大,梁發生失穩時的臨界載荷越小,其臨界載荷隨孔隙率變化的關系曲線單獨在圖5 中給出,可以看出,臨界載荷隨孔隙率的變化是線性遞減的,特別地,e0=0時,梯度多孔梁退化成了均勻材料梁,其相應發生屈曲的臨界載荷Qcr=18.97。這個結果和文獻[22]中的解析解完全吻合,說明打靶法在該問題中的適用性,以及計算結果的可靠性。另外,圖3 和圖4 表明:梁屈曲和彎曲之后,同一個載荷會對應兩個屈曲和彎曲構形圖,這個問題工程上需要引起重視。 圖5 e0-Q 的關系曲線(Beam Ⅰ)Fig.5 Realationship curves of e0-Q(Beam Ⅰ) 給定非均勻溫度和非均勻濕度條件下,圖6 和圖7 分別為Beam Ⅰ和Beam Ⅱ模型梁在不同孔隙率系數下的非線性力學行為。顯然Beam Ⅰ和Beam Ⅱ下,多孔梯度梁的力學行為存在顯著的差異。首先從圖6 和圖3 比較來看,濕-熱環境下多孔梁和非濕-熱環境下的多孔梁力學行為是不同的,濕-熱環境下梁也不會表現出屈曲,而是彎曲行為。剛開始隨隨從載荷的增加,梁的變形幾乎為零,說明機械載荷作用的初始,梁具有很大的抗彎曲變形的能力。之后,隨著變形的增加,需要的機械載荷減小,然后隨變形增加所需隨從載荷又增加,大約在β=125°,隨從載荷出現極值,之后載荷再次減小。說明非濕-熱條件下,梁發生屈曲后,屈曲構形對應著兩種平衡路徑,而濕-熱環境中,梁的彎曲構形是三種平衡路徑。其他載荷(保守載荷)下對應著單構形是不同的力學現象。 圖6 濕-熱條件下Beam Ⅰ梁在不同孔隙率下β-Q 的關系曲線Fig.6 β vs Q of Beam Ⅰfor different porosity under wet-heat condition 圖7 濕-熱條件下 Beam Ⅱ 梁在不同孔隙率下β-Q 的關系曲線Fig.7 β vs Q of Beam Ⅱ for different porosity under wet-heat condition 圖7 中反映出,Beam Ⅱ模型下的非線性力學行為和Beam Ⅰ下的巨大差異。數值計算表明:e0<0.48時BeamⅡ模型下的力學行為和BeamⅠ模型下的力學行為相似,即一個隨從載荷對應三個彎曲構形;當e0接近0.45時,逐漸過渡到一個隨從載荷對應兩個彎曲構形的趨勢;當e0=0.48時的這一時刻,梁發生彎曲時的左端轉角隨載荷的增加非線性單調增加。另外,將圖7 和圖4 比較發現,同樣是Beam Ⅱ梁,如果沒有濕-熱條件的影響,各種e0下的力學行為曲線具有相似的變化規律。而濕-熱環境下,e0>0.48時彎曲又是單構形的,即一個載荷只對應一個轉角。因此,e0=0.48是一個閥值,在這個值前后Beam Ⅱ梁的力學行為會出現突變。 圖8 為Beam Ⅰ梁的孔隙率一定(e0=0.2),給定濕度Cb=1%,Ct=2%情況下,不同非均勻溫度場中的非線性力學響應。圖8 中可見不同非均勻升溫下的多孔梁彎曲變形規律相似,且同一個外載荷仍然對應著三個彎曲構形,隨著非均勻升溫的增加,在三個構形內梁的變形交替增大或減小。從數據分析可知,不同濕度下的第一和第三彎曲構形幾乎相同,而第二構形(指中間的構形)是顯著不同,這和圖8 給出的情況是一致的。 圖8 不同非均勻升溫下,梯度多孔Beam Ⅰ梁的U ?Q關系曲線Fig.8 U -Q curves of graded porous Beam Ⅰ under different non-uniform temperature rises 為了進一步說明圖8 中刻畫出的力學響應,圖9 給出了溫度一定(Td=300 K,Tt=600 K),Q=20,非均勻濕度下,Beam I 梁的彎曲構形圖。比如實線代表?C=1時的三種構形,即相同載荷、相同濕熱條件下有β=1.8°、42.8°、173.2°三種彎曲狀態(這里稱為第一、第二和第三彎曲構形)。由圖9 可見,不同濕度下,第一和第三彎曲構形幾乎重合,而第二彎曲構形差異較大,隨著濕度的增加,梁的變形減小。圖9 的彎曲構形圖和圖8 的平衡路徑曲線是相一致的。 圖9 不同濕度下梯度多孔Beam Ⅰ梁的彎曲構形圖Fig.9 Bending configuration of gradient porous Beam Ⅰ under different humidities (1)非濕熱環境下,Beam Ⅰ梁發生屈曲行為,且臨界載荷隨材料孔隙率線性單獨遞減;而BeamⅡ梁不發生屈曲。 (2)非均勻濕熱條件下,Beam Ⅰ梁和BeamⅡ梁都是發生彎曲變形;其中變形過程中,BeamⅠ梁的三個變形時刻會對應同一個隨從載荷;當孔隙率系數e0>0.48時,Beam Ⅱ梁的彎曲行為是隨載荷非線性增加的。 (3)給定濕度條件,隨著非均勻升溫的增加,BeamⅠ梁的變形先增加后減小然后再次增大。整個變形過程會對應兩個極值載荷。 (4)非對稱孔隙率分布和均勻孔隙率分布下的濕-熱-機力學行為存在顯著差異,尤其對非對稱孔隙率分布梁來講,e0=0.48是一個閾值,該值之前的力學行為和對稱分布類似,即一個載荷對應三個彎曲構形時刻,而超過這個值之后,同一載荷只對應一個彎曲構形。1.2 溫度場和濕度場


2 控制微分方程






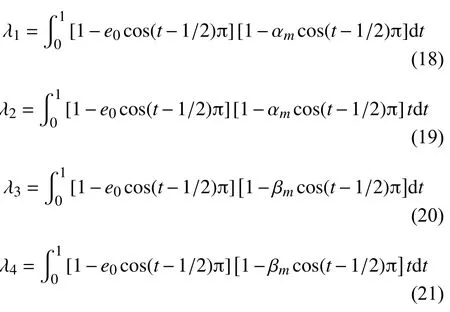
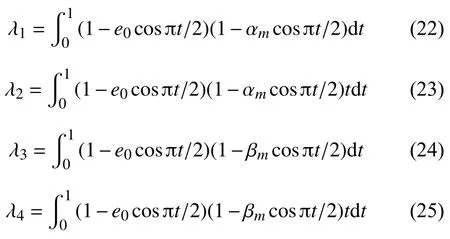

3 數值結果及討論




4 結論

