展示基本圖形魅力 提升學生數(shù)學素養(yǎng)

沈偉明

【摘要】相似三角形是初中幾何中重要知識點，相似三角形基本圖形的掌握是此知識點的基本要素，以基本圖形為研究對象，并將其作為提升學生數(shù)學素養(yǎng)的載體，符合學生的認知特點，能收到良好的效果。

【關鍵詞】 基本圖形;數(shù)學素養(yǎng);三角形教學

《數(shù)學課程標準》在“圖形與幾何”方面的學習要求是讓學生能從較復雜的圖形中分解出基本圖形，并能分析其中的基本元素及其關系。“圖形與幾何”的教學從某種意義上講就是使學生認識基本圖形的性質(zhì)，引導學生運用基本圖形的方法去分析問題和解決問題，提升學生的數(shù)學素養(yǎng)。因此平面基本圖形的認識、儲備、運用在相似三角形的教學中顯得十分重要。

一、初中學生認知特點

認知心理學認為：人的思維不僅要借助概念，也要借助表象來進行。表象就是人們頭腦中出現(xiàn)的事物的形象。初中學生以形象思維為主，形象思維的對象就是表象。如果在學習過程中，讓學生重點加工基本圖形，那么這些基本圖形就可以在學生的大腦中形成比較清晰的表象，從而為解決更復雜的圖形打好堅實的基礎。面向初中學生，以基本圖形為研究對象，并將其作為提升學生數(shù)學素養(yǎng)的載體，符合初中學生認知特點。

二、基本圖形與基本圖形分析法

在幾何內(nèi)容中，圖形是重要的表達形式。基本圖形一般是指在教材中描述圖形定義、公理、定理的圖形，如平行線、直角三角形、平行四邊形、正方形等。另一類是指一些具有代表性的例題或習題中常見的圖形，將同種類型的問題進行合理歸納、梳理，進而形成的一個個基本的圖形。利用基本圖形分析問題，是幾何學習的有效途徑。熟悉基本圖形的特征、特性，可在描圖、畫圖的過程中培養(yǎng)學生的直觀想象素養(yǎng)，在分析問題的過程中培養(yǎng)學生的數(shù)學抽象素養(yǎng)，在解決問題的過程中培養(yǎng)學生的邏輯推理素養(yǎng)。相似三角形中出現(xiàn)了大量的基本圖形：平行線型、相交線型、母子型、一線三等角型等，通過對這些基本圖形為主線開展例題教學和問題解決，能有效提高學生用數(shù)學的眼光提出問題、探索問題、解決問題的能力。

三、基本圖形模型

相似三角形是蘇科版《義務教育教科書數(shù)學》九年級下冊第六章《圖形的相似》的內(nèi)容，常見的基本圖形主要包括以下幾種類型：

（一）平行線型

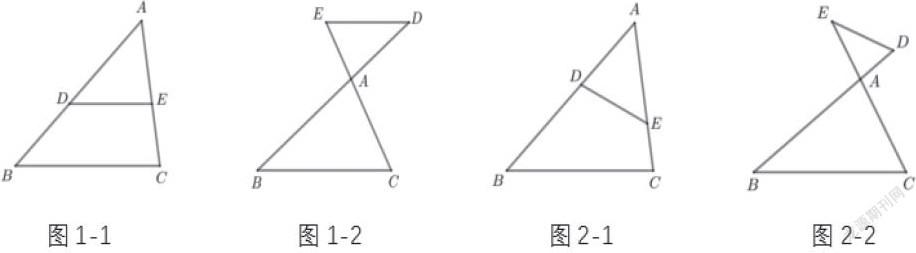
如圖1-1、1-2，若DE∥BC，則?ABC～?ADE，這種基本圖形很像英文字母A、X，因此我們稱它們?yōu)椤癆型圖” “X型圖”。特點：兩個相似三角形有兩邊在同一直線上，第三邊相互平行。

（二）相交線型

如圖2-1、2-2，若∠AED=∠B，則?ABC～?AED，這種基本圖形我們稱它們?yōu)椤靶盇型圖” “斜X型圖”。特點：兩個相似三角形有兩邊在同一直線上，有一個公共角或對頂角。

（三）一線三等角型

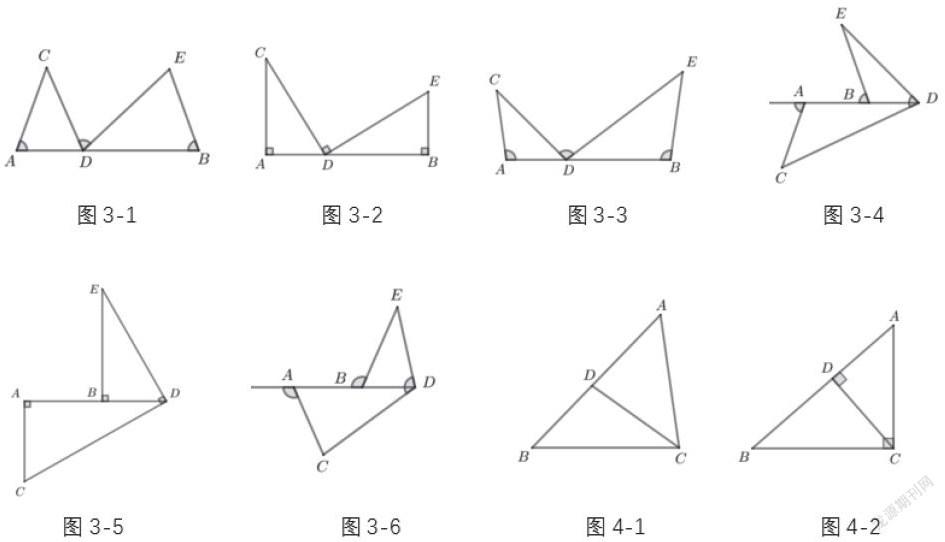
如圖3-1，若∠CAD=∠DBE=∠CDE，則?CAD～?DBE，這是常見的相似模型，我們稱之為“一線三角型”，指的是三個等角在同一條直線上構成的相似模型。這個角可以銳角，也可是直角或鈍角，兩個相似的三角形可在同側也可以異側，如圖3-2、3-3、3-4、3-5、3-6。

（四）母子型

將圖2-1中DE向下平移到點E與點C重合，如圖4-1，則?ABC～?ACD，這種相似基本圖形稱之為“母子型”。特別地，如圖4-2令∠ACB=90°，CD是斜邊AB上的高時，則?ABC～?ACD～?CBD。“母子型”相似模型也稱之為共邊共角型，其最為顯著的特征為：圖形中含有一個公共角和一條公共邊，大小三角形錯疊相依。

四、運用基本圖形解題

（一）直接利用問題中基本圖形解題

這類題型簡明，條件不多，教師只需引導學生找出問題圖形中的基本圖形，再根據(jù)相似三角形性質(zhì)解題即可。如圖5，?ABC中，AB=AC=6，BC=5，D是BC邊上點，以點D為頂點，作∠EDF=∠B，射線DE、DF分別交AB、AC于點E、F，當BE=2，點F為AC中點時，求BD的長。

分析：本題是常見的“一線三角型”，根據(jù)∠EDF=∠B=∠C，可得?EBD～?DCF，得=，令BD=x，DC=5-x，則有=，解得x=2或x=3。

（二）分離基本圖形解題

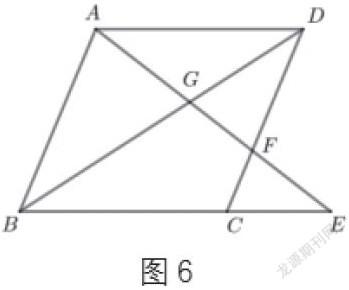
任何一個復雜的幾何圖形都是由若干個基本圖形組合而成的，面對復雜圖形要引導學生觀察、想象、比較、分析問題圖形，精準恰當?shù)貜膯栴}圖形中分離出基本圖形并厘清圖形關系，再利用基本圖形性質(zhì)，問題就能迎刃而解。如圖6，平行四邊ABCD中，點E是BC延長線上一點，AE交BD于點G，交CD于點F，則圖中共有多少對相似三角形？

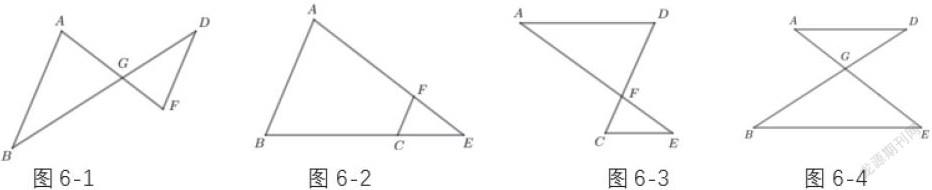
分析 根據(jù)AB∥CD，可分離出圖6-1和圖6-2，得?ABG～?FDG，?ABE～?FCE，根據(jù)AD∥BC，可分離出圖6-3和圖6-4，得?ADF～?ECF，?ADG?EBG，根據(jù)相似傳遞性得?ADF～?EBA，?ABD～?CBD，共六對。

（三）添加輔助線構成基本圖形解題

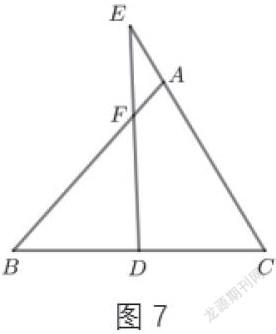
這類題型具有一定的隱蔽性，教學過程中要引導學生認真閱讀分析題目信息和圖形特點，嘗試先找到基本圖形的一部分，通過學生的聯(lián)想、幾何直觀，再添加輔助線把圖形補全，構成完整的基本圖形。如圖7，?ABC中，D是BC邊中點，E是CA延長線上的點，ED交AB于點F，EF：FD=2：3，求AF：FB的值。

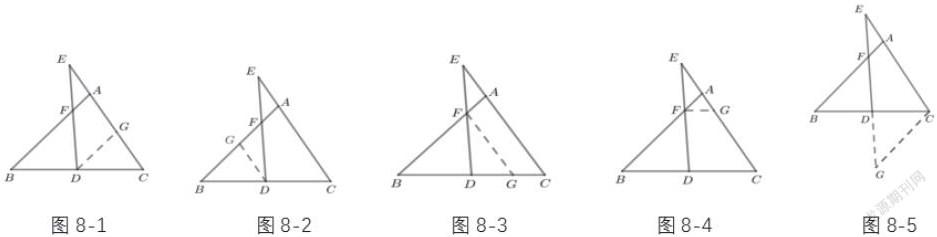
分析：聯(lián)想已學相似三角形基本圖形，通過合作交流，學生們分別找出了幾種不同的解法。法一：過點D作DG∥AB交CE于點G，則有?EFA～?EDG，?CDG～?CBA。法二：過點D作DG∥AC交AB于點G，則有?EFA～?DFG，?BDG～?BCA。法三：過F點作FG∥EC交BC于點G，則有?BFG～?BAC，?DFG～?DEC。法四：過點F作FG∥BC交CE于點G，則有?EFG～?EDC，?AFG～?ABC。法五：過點C作CG∥AB交ED延長線于點G，則有?EFA～?EGC，?CDG～?BDF。

五、反思感悟

（一）熟悉基本圖形，發(fā)展學生空間觀念

《數(shù)學課程標準》要求通過圖形的運動，觀察、想象、分析圖形和思考問題，提高學生研究圖形性質(zhì)的興趣，發(fā)展學生的空間觀念。運用基本圖形教學時，教師遵循學生認知規(guī)律，分別從“直接應用基本圖形”“從復雜圖形中分離出基本圖形”“構造基本圖形”三個層次，培養(yǎng)和發(fā)展學生的空間觀念，達到發(fā)展學生思維、促進學生技能提高的目的。

（二）掌握基本圖形，建立學生幾何直觀

《數(shù)學課程標準》指出“幾何直觀是指利用圖形描述和分析問題，借助幾何直觀可以把復雜的數(shù)學問題變得簡明、形象，有助于探索解決問題的思路，預測結果。幾何直觀可以幫助學生直觀地理解數(shù)學，在整個數(shù)學學習過程中都發(fā)揮著重要作用”。它表明，在整個數(shù)學教學中都應該重視幾何直觀，培養(yǎng)幾何直觀能力應該貫穿義務教育數(shù)學課程的始終。在教學中要有意識地強化對基本圖形的運用，不斷地運用這些基本圖形去發(fā)現(xiàn)、描述問題，理解、記憶結果，借助對基本圖形的分析與學習，學會用圖形思考、想象問題是研究數(shù)學，也是學習數(shù)學的基本能力。這種幾何直觀能力能使我們更好地感知數(shù)學、領悟數(shù)學。

（三）運用基本圖形 形成學生模型思想

模型思想是數(shù)學課程標準提出的核心理念之一，數(shù)學教育家羅增儒教授提倡在學習數(shù)學的過程中，要善于對新問題展開聯(lián)想，辨別它是否屬于某個已經(jīng)掌握的類型，如果不直接屬于，那么能否進行一些變化，使之屬于某個類型。數(shù)學模型的形式是多樣的，有方程、不等式、函數(shù)等代數(shù)模型，也有幾何中融合著特殊位置關系和特殊數(shù)量關系的基本圖形，還有統(tǒng)計與概率中數(shù)據(jù)模型和概率模型。在相似三角形教學中將常見幾何圖形抽象為為平行線型，相交線弄，一線三角形等最具代表性的基本圖形，形成數(shù)學模型，使之成為學生解決幾何問題的重要工具， 在圖形與幾何的教學中，將模型思想滲透到教學之中，發(fā)展了學生的創(chuàng)新意識有應用意識，提升了學生分析問題和解決問題的能力。

結語

教師要多引導學生積累常見的基本圖形知識以及構建基本圖形的方法，注重對基本圖形的分析和挖掘，提高學生發(fā)現(xiàn)問題、分析問題和解決問題的能力，促進學生數(shù)學核心素養(yǎng)的提升。

參考文獻：

[1]中華人民共和國教育部.義務教育數(shù)學課程標準.北京：北京師范大學出版社，2011.

[2]彭靖東.解析基本圖形 樹立模型意識.中學數(shù)學研究，2020.

[3]張宣.以基本圖形學習為主線的單元教學設計.上海中學數(shù)學，2020（6）.

[4]鄧紫琳.感悟基本圖形，提升初中學生數(shù)學解題能力.數(shù)學教學通訊，2020.