開放性教學在初中數學課堂構建中的有效應用

王金東

【摘要】隨著新課改在近年來的日趨深入，傳統課堂教學“單向灌輸”已逐漸不適合新課改需要，需要向開放性的“理解、溝通和創新”方向轉變。面對新課程理念中的課堂教學要求，如何在初中數學課堂構建中滲透開放式教學是當前課改中的一個關注熱點。基于此，本文主要探討開放性教學在初中數學課堂構建中的有效應用，在初中課堂教學中希望能實現將書本知識轉化為學生自己的學識和主見，甚至是數學思想，使開放式教學真正走入初中數學課堂，實現課堂師生間的良好溝通互動，一方面提升學生的數學學習興趣，另一方面也提升學生的數學創新能力，實現初中數學課堂教學的“雙贏”。

【關鍵詞】開放性教學;初中數學;課堂構建;有效應用

近年來，不少教學工作者在積極探索數學學科課程教學的改革模式，針對初中數學課堂教學，傳統模式通常注重知識點的講解，各種解題思路、解題技巧的傳授，這利于初中學生學科知識的儲備。然而，眾所周知的是，知識儲備型人才已經越來越不能滿足創新型人才培育需求。而數學學科自身的固有特點，比如概念的抽象性、思維的多變性等，導致數學課堂中每一個概念、每一個知識點的學習均需要明白其緣由和過程，而傳統課堂上通常注重理論、知識點的講解，并未對數學知識點的產生過程作出深入探討和挖掘。這種傳統教學模式可產生一些問題，如可能導致學生對抽象數學概念難以真正理解，表現為對知識點的認知處于“只知其然不知其所以然”，這種教學導致學生在以后科學研究中，需要應用數學思維解決問題的時候不知如何應用。基于“理解、溝通和創新”方向的開放式教學可以幫助學生理解抽象知識，了解知識點產生過程，對知識點應用延伸做出思考，也有助于學生將數學知識點學習從知識傳承向思想傳承的轉變。開放性教學在初中數學課堂構建中的有效應用，可以成為提高初中學生綜合素質，提高初中學生解決實際問題能力的有益補充。

一、注重開放性情景引入，激發學生探究興趣

導課在任何學科課堂教學中均可起到承上啟下的關鍵作用，有效的課堂新教學內容導入能吸引學生眼球，讓學生注意力快速集中到課堂教學內容中。開放性情景導課的方法較多，如問題導入法、溫故而知新導入法、歷史故事導入法、生活實例導入法、懸念設置導入法等，但應用頻率最高、應用效果最好的還是問題導入法。大多數初中生對于各式各樣的未知問題均充滿著好奇心。好奇是人類知識獲取的根源，獲取知識首先必須具有好奇心，故以趣味性問題來吸引學生眼球，來激發學生的求知好奇心，可激發學生探究興趣，使學生快速將注意力集中到課堂教學上。如在教學正方形時可設置如下情景問題：

已知一個30 km正方形區域內常年存在手機信號弱狀態，擬在該區域內安裝信號轉發裝置，若這個轉發裝置發射直徑為30 km，那么請問在什么位置安裝裝置才能使信號能完全覆蓋這個信號弱的正方形區域。

對于這個問題需要讓學生思考兩個方面的問題：其一，教師提出這個問題的實質是什么？學生們能否通過圖示的形式將這個問題轉化為數學問題？其二，學生們能否根據題目要求，思考問題解決方案？其實這個探究性情景引入的實質就是一個圓覆蓋正方形問題，由于題目并未限制信號轉發裝置的安裝數量，因此，教師其實可以引導學生從不同角度思考解決問題的方案，只要最終思考的安裝方案符合題目要求即可。當然教師也必須給學生留夠足夠時間和空間，在學生獨立思考之后，隨機邀請學生進行展示和說理。這個問題解決方案較多，可以采取以下方案：

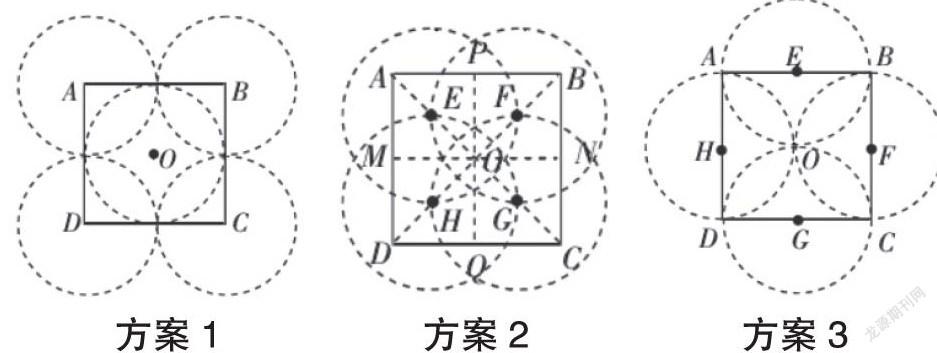
方案1（圖1）：因為轉發裝置的發射直徑大于正方形區域邊長，故可以在正方形四個頂點上各安裝1個發射裝置，再在正方形中心安裝1個發射裝置即可滿足題目要求。

方案2（圖2）：若E、F、G、H分別為AO、BO、CO、DO的中點（O為正方形中心），以點E為例，由于AE、OE均<15，故在點E處安裝1個轉發裝置就可覆蓋到頂點A和O處，同理，點F、G、H也滿足上述要求，故可在E、F、G、H處各安裝1個轉發裝置就可滿足題目要求。

方案3（圖3）：可以考慮將轉發裝置安裝在正方形邊的中點，這也可以覆蓋到所在邊的端點，由于OE、OF、OG、OH均=15，故正方形邊的中點E、F、G、H處各安裝1個轉發裝置就可滿足題目要求。

對于這個情景導入，需要給學生留足展示和說理環節，促使學生自主探究，較好地培養了學生的發散思維。同時在學生自主探究，教師也應及時做好巡視。其實對于方案1、方案2，學生們都能夠根據已學知識和經驗時輕松解決問題，但對于方案3，教師應及時通過“安裝點的位置能否選擇在四邊形邊上”等方式引導學生思考，促使學生發現解決問題的方法。

二、注重開放性問題設置，活躍學生學習思維

在數學課堂的開放性問題教學主要是指在教學內容、教學活動及師生之間關系的開放，旨在引導學生發揮主觀能動性和創造性，激發學生的潛在能力，培養學生興趣，提高課堂效率。開放性問題設置是開放性數學課堂中不可缺少的內容，一個好的開放性數學問題可使課堂教學效果事半功倍。開放性初中數學課堂中需充分利用這一教學方法，活躍學生學習思維。數學教學中，教師可適時地設置一些開放性問題，以此來拓寬學生思維空間，調動學生學習主動性，進一步提升學生創新思維能力。

例如，在教學“勾股定理”這一初中數學重要內容時，教師可在學生們勾股定理所含基本知識內容有了認識后，為學生設計了這樣一個開放性問題：若一個直角三角形的兩條邊邊長分別為6厘米和8厘米，請求第三條邊的長度？

對于這樣一個問題，學生們在掌握“勾股定理”基本知識內容后，很快就能進入思考中，可能很快就能有自己的答案，可能大部分學生均認為第三條邊的長度為 10 厘米。其實上面這個題目中有一個“陷阱”，即題目中并未說明這兩個邊是否均是直角邊的邊長，即其中一個8厘米的邊可能為斜邊長，這是容易讓學生們忽略了題中“陷阱”。這需要教師在隨后引導中反思這個審題中的錯誤，并主動改正錯誤和進一步思考，同時也可讓學生對勾股定理的知識有了更全面的把握，并加深了對這勾股定理知識的理解。這樣一個簡單的開放性數學課堂問題，教師以這樣一個開放性的數學問題，可有效開闊學生的思維空間，較好培養學生的思維能力，促進了學生深入思考。973188D1-B031-49E7-BD6A-418E3E380053

三、注重設置開放性活動，促進師生有效互動

課堂教學是一個師生互動過程，小組合作教學利于培養學生的協作精神，這種開放性教學活動對學生發展有很好的推動作用。在數學課堂教學中，教師可組織一些開放性數學活動，讓學生發揮主體作用，促進學生進行自主探究學習。

例如，在教學初中數學“平行四邊形”教學時，“平行四邊形的性質”是教學重點，為讓學生能深入理解這個重點知識，教師可在課堂中組織小合作的開放性教學活動，讓學生自己去探究平行四邊形性質。

在小組合作學校中，有的學生可通過觀察具體圖形提出關于“平行四邊形性質”的大膽猜想：兩條對邊長度是相等的。對于這個問題學生們需要一起去驗證。有的學生也有可能想到數學作為一門嚴謹的學科，直接測量的方法是不嚴謹的，因為測量是有誤差的，因此需要利用一些嚴謹數學理論來驗證分析。此時學生們很快就有一些想法，如何將平行四邊形的一條對角線連接，然后證明這兩個三角形是否全等，若全等，那么兩條對邊長度就是相等的。學生們可在互相交流討論和共同合作的過程中，一起探究“平行四邊形的性質”這個內容，可深化了對該知識的掌握。數學課堂教學中，根據教學內容組織開放性的教學活動，可讓學生共同探究學習，利于學生對數學知識有更深的認識和理解。

四、注重設置開放性練習，提升課堂教學效率

練習是課堂教學中的重要環節，能夠幫助學生鞏固本堂課所學知識。初中數學教學中應充分開發、利用練習這一教學環節，發揮數學練習在課堂教學中的價值。初中數學課堂教學中，教師需注重一些開放性的數學練習，以此來激發學生的練習欲望。如教師可以將出題權交給學生，讓學生扮演教師，既可做到課堂練習，也可做到互相評價。此種開放性的教師方式，不僅可以調動學生的練習積極性，也可提升課堂教學效率。

例如，在課堂教學“合并同類項”這一初中數學內容時，教師可從學生角度出發，大膽變革課堂練習模式，讓同桌之間互相合作，針對“合并同類項”這個每人出一份試卷，并讓對方來做，在雙方做完后再收回，互相評分。

相信再此種教學開放性的習題教學模式中，學生們能積極主動參與到中，能根據課上“合并同類項”這一教學內容開始出題，并且很快各自完成出題任務，并由同桌進行練習。學生在解答手中的同桌題目時候也能表現得認真，在相互進行解題情況評價時也可認真仔細，可以從對方的解答結果中尋找到自己的學習點，這樣的開放性練習，可再無形中學到更多知識。在這一開放性練習的課堂教學案例中，教師創新練習形式，學生互相出題并互相評價，這樣課堂教學形式可讓學生互相學習，不僅能夠使學生更好的地鞏固課堂知識，還能鍛煉學生的學習能力，可讓學生從中學到更多。

總之，學生是學習的主人，教師要學會放手，注重發揮學生的主體作用。開放性教學在初中數學課堂構建中的有效應用，希望能實現將書本知識轉化為學生自己的學識和主見，甚至是數學思想，使開放式教學真正走入初中數學課堂，實現課堂師生間的良好溝通互動，一方面提升學生數學的學習興趣，另一方面也提升學生數學的創新能力，實現初中數學課堂教學的“雙贏”。

參考文獻：

[1]周華娟.開放性教學，構建實效初中數學課堂[J].數學大世界（上旬），2021（02）：57.

[2]張冬艷.初中數學教學中開放性問題的有效應用[J].數學大世界（上旬），2021（02）：94.

[3]逯艷.豐富初中數學課堂，創新初中數學教學方法[J].新課程，2021（02）：88.

[4]江勤娟.淺談初中數學開放性作業的常見類型[J].科幻畫報，2020（11）：237.973188D1-B031-49E7-BD6A-418E3E380053