嘗試德智融合，落實立德樹人

劉雙雙

【摘要】巧妙融合學科德育，激發學生的興趣與愛國情感、思維碰撞、專注與思考、合作討論、歸納總結等過程，實現學科育人的目標，有效提升學生的思維品質.

【關鍵詞】學科德育;思維品質;函數概念

赫爾巴特曾言：“我拒不承認任何沒有教育性的教學”[1]，“教學如果沒有進行德育教育，只是一種沒有目的的手段”.[2]筆者對此進行了探索，現以滬教版八年級第一學期第十八章第一節“函數的概念”的教學為例，重點探究函數概念得出的過程中，如何滲透學科德育，提升學生學習數學的興趣、自信心、專注與思考、合作意識、歸納總結、激發學生的愛國情感等思維品質.

1 問題的提出

“立德樹人”作為教育的根本任務要得到落實必然要依靠教學，而教學主要依托課程來實現，這一“課程”不僅僅指專門的德育課程，還應包括各學科的合力.也就是說，德育教學要集各學科的合力，學科德育，如何有效地融合于智育、美育等過程之中呢？筆者擬以“函數的概念”教學過程為例，談幾點感悟.

2 “函數的概念”的價值分析

函數是數學中重要的基本概念之一，它是從現實世界中抽象出來的，是從數量關系的角度刻畫事物運動變化規律的工具;函數知識滲透在中學數學的許多內容之中，它又與物理、化學、語文等學科的知識密切相關.同時，函數是一個重要的數學思想，運用函數的思想和方法，可以加深對一些代數問題的理解.

初二的學生的思維發展還不成熟，看問題往往是局部的、靜止的、割裂的，還不能用辯證思維來理解函數概念.因此本文運用生活實例，用運動變化的觀點看待事物，理解變化過程中的兩個變量之間相互依賴的含義，在具體情境中領悟函數概念的意義.通過觀察、歸納、概括，參與變量的發現和函數概念的形成過程，提高分析問題和解決問題的能力，理解函數的概念.在探索實際問題中的數量關系，培養對學習的興趣和積極參與數學活動的熱情.在解決問題的過程中體會數學的應用價值并感受成功的喜悅，建立自信心，在小組討論過程中，培養合作意識和探究的樂趣.[3]

3 教學過程

巧妙設計教學過程，有效滲透學科德育，提升學生思維品質

3.1 學科融合，巧妙引入，激發興趣

回顧筆者的引出環節，是利用七年級下人教版語文教材學過《孫權勸學》，里面有一句話“士別三日，即更刮目相看. ——《資治通鑒》”

師 同學們，這句話是什么意思？誰能來翻譯一下？

生 讀書人（君子）分別幾天，就應該重新另眼看待了.

師 這句話后來又引申為什么意思？

生 世間萬物都是變化發展的，應該用運動、變化的觀點來看待事物.

首先，在數學課堂內看到語文教材中句子，就激發了學生的極大的學習興趣，學生在思考這句話與本節課到底有什么關系？興趣是最好的老師，當學生產生了興趣，激發了好奇心，才能會非常迫切地想認真學習本節課的知識.通過讓學生翻譯這句話，讓學生明白每天都認真學習，你的知識儲備量是會發生變化的，從而激發學生學習的內驅力.接著讓學生翻譯這句話引申的意思，讓學生明白世間萬物都是變化發展的，應該用運動、變化的觀點來看待事物，從而引出學習本節課的必要性.這樣的引入，其實也潛移默化地告訴學生，學科之間的知識都是融會貫通的，引導學生關注學科之間的相互滲透，探究生活中各類事物之間可能包含的各種學科知識，這樣才能較好地培養學生的靈活的思維方式，使學生能夠積極參與對日常生活和自然現象、社會現象的探究，培養學生終身學習科學文化知識的思維品質[4].

3.2 創設情境，觀察概括，激發學生愛國情感

情境1 長征五號發射升空過程

教師 同學們，2020年7月23日，中國發生了一件激動人心的事情，長征五號遙四運載火箭成功地將火星探測器“天問一號”發射升空，我們祖國的航天事業越來越強大.我們來看一下長征五號遙四運載火箭的發射過程.

問題1 在發射過程中，長征五號有什么發生了變化？什么沒有發生變化？（動態播放視頻，并隨意按暫停鍵）

通過觀察，得出長征五號的形狀沒有發生變化，長征五號的高度和發射時間發生了變化.

問題2 我們來認識一下長征五號

在這段發射視頻中，長征五號的助推器直徑、火箭芯級直徑、箭體長度、起飛質量、起飛推力、近地軌道運載能力、地球同步轉移軌道運載能力、飛行高度、飛行時間等來具體表達事物的某些特征（屬性）稱之為“量”，同時我們用“數”來表示量的大小.數和度量單位合在一起，叫做“數量”.

在這段視頻中，長征五號的助推器直徑、火箭芯級直徑、箭體長度、起飛質量、起飛推力、近地軌道運載能力、地球同步轉移軌道運載能力這些保持數值不變的量叫做常量（或常數）

這段視頻中的飛行高度、飛行時間是發生變化的，在問題研究的過程中，可以取不同數值的量，叫做變量.

同時告知學生常量和變量是相對某個變化過程的，不是絕對的.

問題3 在這個變化過程中，飛行高度h和飛行時間t有什么關系？

當飛行的時間越久，飛行的高度越高，變量h是隨著變量t的變化而變化的.

問題4 在這個變化過程中，當飛行時間t確定一個值時，飛行高度h的值可以確定嗎？有幾個高度值和時間t對應？

當飛行時間t確定一個值，飛行高度h的值可以確定，并且高度值唯一確定.

給出表格進一步感受一下問題3、問題4得出的結論.

設計意圖 通過對長征五號飛行時，飛行高度和飛行時間的直觀感受，分析直觀數據，可以初步感受到變化的量、不變的量和兩個變量之間的關系，初步得出結論，兩個變量之間是變量h是隨著變量t的變化而變化的，當飛行時間t取定一個值時，飛行高度h的值唯一確定.并且通過這個例子，讓學生了解“天問一號”遙四運載火箭的基本構成，感受發射過程中祖國人民的激動與自豪，感受到祖國的日益強大，讓學生在情感上產生共鳴，了解到數學的應用價值，從而激發學生的愛國熱情及為將來投身祖國航天事業做鋪墊.

情境2 汽車加油過程4

圖5

問題5 在汽車加油過程中，有哪些量？哪些是變量？哪些是常量？（播放視頻隨意按暫停鍵）

單價是常量.在視頻播放過程中，油量x和總價y是變化的.

問題6 在加油的過程中，總價y和油量x之間有什么關系？

當加油量越多時，所花費的總價就越高，變量y是隨著變量x的變化而變化的.

問題7 在這個變化過程中，加油量x取了一個值時，總價y的值可以確定嗎？有幾個y的值和確定的x的值對應？

當變量x取一個確定的值時，變量y的值也隨之唯一確定.

問題8 通過表格中的數據及剛才的視頻中的數據，可以用一個等式來表示總價y和油量x的關系嗎？

y=6.51x

通過表格和等式進一步感受變量y與變量x之間的關系，即變量y是隨著變量x的變化而變化的，當變量x取一個確定的值時，變量y的值也隨之唯一確定.

設計意圖 通過加油時的總價和加油量的直觀數據，可以清楚地感受到變化的量、不變的量和兩個變量之間的關系，變量y是隨著變量x的變化而變化的.并且通過視頻暫停和表格，可以感受當變量x取一個確定的值時，變量y的值也隨之唯一確定.再次通過身邊實例，讓學生感受數學與我們的生活息息相關，激發學生學習數學的興趣，同時通過播放視頻，讓學生直觀地感受兩個變量之間的關系，同時通過與上個問題情境相對比，感受兩個問題的相同點與不同點？培養學生對比、歸納的數學思維品質.

情境3 上海一天溫度的變化過程

0

教師：這是上海近24小時的溫度變化情況（聯網搜索上海近24小時的整點溫度）

問題9 這幅圖下面水平這條線上的數字表示什么？左邊豎直這條線的數字又表示什么？

下面水平這條線上的數字表示時間t，豎直這條線的數字表示溫度T.

問題10 在這24小時內，溫度T是否隨時時間t的變化而變化？當時間t取定一個值時，溫度T的值是否確定？是唯一確定的嗎？

在這24小時內，當時間t發生變化時，溫度T也隨之發生變化.當時間t確定時，溫度T也隨之唯一確定.

設計意圖 學生能夠理解每天的溫度是隨著時間的變化而變化的，當時間t取定一個值時，溫度T的值唯一確定.這個實際問題用圖像來表示變量之間的關系，可以把這幅圖像看作一個坐標系，橫軸表示時間，縱軸表示溫度，縱坐標的值隨著橫坐標的值的變化而變化，通過鼠標移動，感受溫度T與時間t的關系. 通過身邊實例，讓學生感受數學與我們的生活息息相關，激發學生學習數學的興趣，在情感上產生共鳴，同時通過百度實時搜索，讓學生直觀地感受兩個變量之間的關系，同時通過與前兩個問題情境相對比，感受兩個問題的相同點與不同點？培養學生對比、歸納的數學思維品質.

3.3 探究屬性，歸納總結，提升思維品質

問題1 在這幾個問題情境中，有什么共同的特征？

學生通過上述表格，歸納總結出如下知識：

在某個變化的過程中有兩個變量，設為x和y，

1

那么變量y叫做變量x的函數，x叫做自變量.

引入課題——函數的概念

設計意圖 通過三個生活實例，學生發現變化過程中兩個變量之間的關系，讓學生試著歸納總結出這幾個問題的共同特征，從而告訴他們這就是函數，學生在歸納出函數的概念的過程中，不僅增強了自信心，同時通過思考、梳理、轉化成數學語言的過程，高效地提升了數學的思維品質，同時也掌握了概念的形成過程.

3.4 追溯歷史，以古鑒今，提升學生自信心

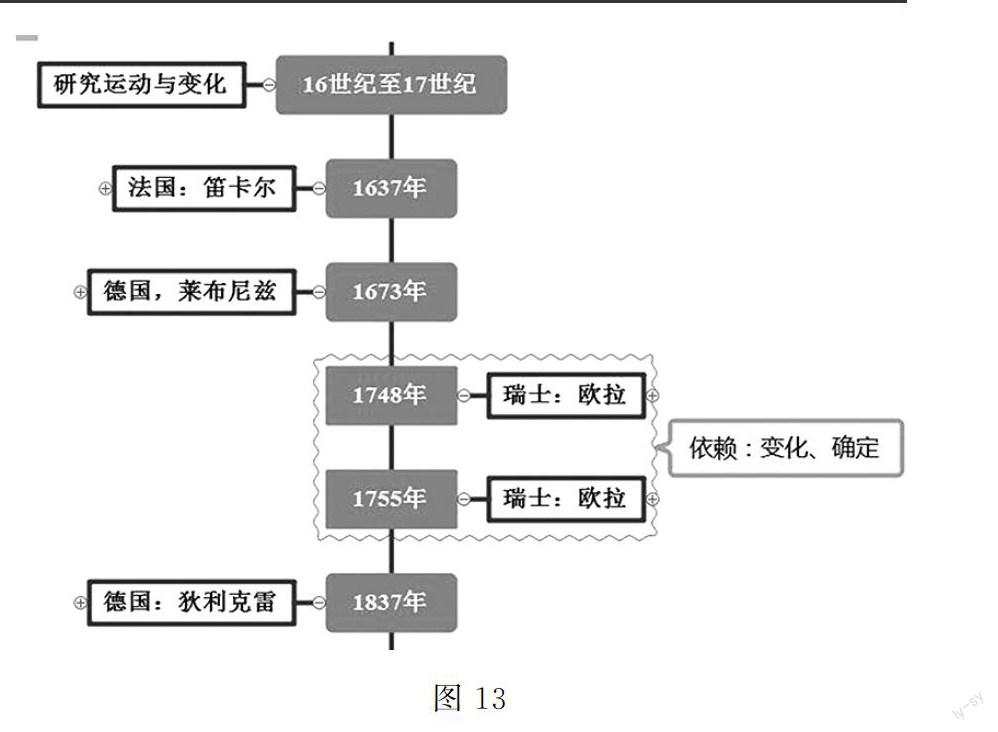
教師 我們通過下面的視頻來了解一下為什么把兩個變量確定的依賴關系叫做函數.

（播放視頻：函數數學史）

2

3

設計意圖 這個視頻讓學生了解了函數的發展歷史，為什么把兩個變量確定的依賴關系叫做函數，并且最后利用寄信來解釋函數的依賴關系，從而更深刻地理解函數.同時也讓學生了解到我們也可以像數學家一樣，得出數學概念，極大地增強了學生學習數學的興趣和信心.

3.5 敢于探究，明確數學的嚴謹性、相對性

問題1 長征五號遙四運載火箭在把“天問一號”發射到既定軌道后，可以無休止地飛行嗎？

它把“天問一號”發射到既定軌道后，殘骸便會慢慢隕落，飛行時間大概2167s.

問題2 汽車加油過程中，可以無休止地加油嗎？

汽車加油所加的油量要0≤x≤油箱容積

完善函數的概念，我們在研究問題時，要在自變量有意義的范圍內去研究，得出函數的定義域的概念.

在某個變化的過程中有兩個變量，設為x和y，

在自變量允許的取值范圍內——即定義域內，

4

那么變量y叫做變量x的函數，x叫做自變量.

問題3 三個情境中，哪個變量是哪個變量的函數？誰是自變量？

問題4 在加油的過程中，有時加油會說加150元或者200元的油，此時哪個變量是哪個變量的函數？誰又是自變量？

問題5 為什么要學習函數？

掌握了函數這個工具，就可以從數學的角度去研究變化過程中的數量關系.

設計意圖這個過程是讓學生明白，數學的嚴謹性，函數關系是相對的，是在自變量允許的取值范圍內才成立，不是在任何范圍都成立的.哪個變量是哪個變量的函數、誰是自變量也是相對于研究問題的角度而定的，不是完全確定不變的.最后讓學生發現學習函數的重要性和必要性.

問題6 函數有哪些表示方法？

通過前面三個問題情境，情境1和情境2通過列表來表示兩個變量之間確定的依賴關系，這種表示方法叫做列表法.

情境2中還用數學式子y=6.51x，這種用數學式子來表示兩個變量之間確定的依賴關系，這種表示方法叫做解析法.

情境3中用圖像來描述兩個變量之間確定的依賴關系，這種表示方法叫做圖像法.

設計意圖 知道從數學角度如何描述函數，同時告知學生，有的函數不能用函數解析式來表示，例如情境3，但有的問題既可以用表格法，又可以用解析法來表示，例如情境2，在我們以后的學習中，會經常三種表示方法一起用.體會數形結合的思想.

3.5 學以致用，合作討論，培養合作意識和探究樂趣

（1）找規律：下圖是由火柴拼成的，請根據規律填表.

（2）如果 n 是一個變量，那么 2n+1 也是一個變量.試問：變量 2n+1 是不是變量 n 的函數？

設計意圖 找規律問題也蘊含函數關系，如果用運動變化的觀點來看待問題，我們之前學的很多知識，兩個變量之間都具有函數關系.能夠將學習的知識有效的應用，這也是數學學習的另一個重要的目的，通過將所學知識內化為自己的知識，并應用到數學問題中，學生通過思考、分析、探究，最終解決問題，這個思維過程對學生是十分必要的.

（1）電影《我和我的家鄉》每張電影票的售價為45元，若設每場電影票售出x張，票房收入為y元，y是不是x的函數？

（2）若某電影院1號放映廳10月1日《我和我的家鄉》放映的場次和每場觀看的人數有如下關系：

每場電影的“觀看人數”是不是“放映場次”的函數？

設計意圖 通過此例引導學生關注祖國的發展變化.讓學生感受祖國的變化之大，發展之快，為祖國的日益美好而自豪，激發學生的愛國之情.并且通過最近熱門的生活實例更容易調動學生的學習熱情，明確，數學源于生活，并用于生活，讓學生知道這些知識，便可以解決很多生活中的問題，激發學生學習的興趣.同時也同時體會用解析法、表格法來表示函數關系，進一步感受數學結合的思想.學生對問題（2）的理解有些難度，所以由設計小組討論，通過思維碰撞，相互討論，培養合作意識和探究精神.

下圖是某日的氣溫變化圖，試問：時間t 是不是溫度T 的函數？

8

設計意圖 讓學生理解當自變量取一個確定的值時，另一個變量的值隨之唯一確定.給出反例，加深對函數概念的理解.進一步理解函數概念的嚴謹性及相對性.

3.6 歸納總結，思維升華，提升自信心

（1）本節課你學了哪些知識？什么是函數？

函數：一種關系 、兩個變量 、三種表示法

（2）為什么學函數？

函數——從數學的角度去研究事物在動態變化中的數量關系

設計意圖 通過本課的學習，讓學生自己進行歸納總結本節課所學的知識及思想方法，進行思維的升華，整節課的教學老師只是起到了一個啟發的作用，都是學生自主思考、討論、歸納總結得出相關概念、結論，解決相關問題，有效地提升了學生學習數學的自信心.

4 一般規律

（1）解讀教材，了解學情，以學定教.如果想有效落實學科德育，需要深刻解讀教材，了解教學內容在數學教材中的地位及延續性，了解學情，以學定教.

（2）巧用素材，提高數學思維品質.在教學過程的設計中，挖掘身邊有教育意義的素材，正確地建立數學模型，融入教學，巧妙地滲透學科德育，在教學過程中，讓學生進行思考、討論、歸納總結等思維過程，提升學生學習數學的興趣、自信心、專注與思考、合作意識、歸納總結、激發學生的愛國情感等思維品質.

（3）多讀書，多學習，進行學科融合教學.作為教師，需要多讀書、多學習，了解各學科之間的知識的關聯性，在教學過程中有效地進行知識融合，使學生在探究生活中各類事物時，能想到各種學科知識，這樣才能較好地培養學生的靈活的思維方式，使學生能夠積極參與對日常生活和自然現象、社會現象的探究，培養學生終身學習科學文化知識的思維品質.

（4）了解數學史，增強學生自信心.在教學中，老師能夠了解本節課的數學史，融入到教學中，通過探索學習，學生發現自己也能夠像數學家一樣得出一些結論和概念，會極大地增強學生學習數學的自信心，同時，也可以更深刻地理解本節課的知識.

5 問題探討與反思

函數概念較為抽象，學生的印象中，只有能寫出函數解析式的數量關系，才是函數關系，所以對于學以致用2（2）中，經過小組激烈地討論，還是有很多同學得出每場電影的“觀看人數”不是“放映場次”的函數，所以對于這種不能用解析式來表示的函數關系或者“多對一”的函數關系還需要讓學生再有機會去感受、體會，從而更深刻地理解函數概念.不過這種思維的碰撞，同樣是學習數學的重要過程，只有經歷過這樣的思考、質疑、探索、討論，才能不斷推進數學的發展.

參考文獻：

[1]赫爾巴特.赫爾巴特文集：教育學卷一[M].李其龍，譯.杭州：浙江教育出版社，2002：54.

[2]張煥庭.西方資產階級教育論著選[M].北京：人民教育出版社，1964：121.

[3徐曉燕，費小芳.基于核心概念及其思想方法的概念教學研究—“函數”的思考與實踐.上海中學數學，2017（4）.

[4]孔令博.走出課堂的界限，整合課程的資源—初中各學科的資源整合的探索與嘗試.新課程？中學，2017（4）.

[5]滕洋.學科德育的“必要性”及其價值期待.中小學德育，2019（11）.