STEM教育理念下的初中數學“綜合與實踐”課教學路徑探析

吳治新

[摘? 要] 文章以“反比例函數”為例，闡釋了STEM理念下初中數學“綜合與實踐”課的教學路徑，即創設情境，引出問題;合作探究，建構模型;協作解釋，深化認識;反饋評價，積累經驗.

[關鍵詞] STEM教育;綜合;實踐;反比例函數

STEM教育指的是一種跨科學、技術、工程和數學等多學科融合的學習方式，其強調問題解決過程中的學科融合，通過探究式和項目式的學習方法，培養學生的應用意識和創新能力. 初中數學“綜合與實踐”課具有自主性、實踐性、綜合性和開放性，這與STEM教育理念具有很大的契合度[1]. 筆者以“反比例函數”為例，闡釋了STEM理念下初中數學“綜合與實踐”課的教學路徑，期望能夠達到拋磚引玉的效果.

創設情境，引出問題

STEM教育理念強調要讓學生通過具體情境抽象出數學問題. 因此，教師在創設教學情境時，要從現實生活出發，以學生已有的生活經驗和知識儲備為基礎，并綜合運用多學科之間的聯系切入問題，這是STEM教育的重要特點.

師：如圖1所示，一根勻質木桿，長度為100 cm，用細繩綁在木桿的中點O并將其吊起. 在距離中點O的左側25 cm處掛一個重9.8 N的物體，在中點O右側用一個彈簧秤向下拉，使木桿處于水平狀態. 如果改變彈簧秤與木桿中點O的距離L（單位：cm），觀察彈簧秤的示數F（單位：N）有什么變化，并完成下表：

（教師為各小組提供實驗器材，學生分組合作，動手實踐. 有的學生負責測量在水平狀態下彈簧秤與中點O的距離，有的學生負責拉彈簧秤并讀出彈簧秤的示數，有的學生負責記錄數據并完成表格）

教學中，教師以物理學科的“杠桿原理”為背景創設具體情境，以小組合作的方式展開動手實踐活動，體現了數學學科與科學、技術等學科的聯系，調動了學生學習積極性，使學生在最短時間內進入積極的學習狀態之中.

合作探究，建構模型

模型思想是一種重要的數學思想，其能夠幫助學生感受數學與現實世界的密切聯系，也能為學生的后續學習和長遠發展奠定基礎. STEM教育理念下，教師在引導學生構建數學模型的過程中，要將科學、技術、工程等學科的思想方法與數學學科有機結合起來，綜合運用多學科之間的聯系解決問題，從而體現STEM教育的跨學科性[2].

師：現在，我們以L為橫坐標，以F為縱坐標建立直角坐標系. 請大家在直角坐標系中描出以表格中的數對為坐標的點，并將這些點用平滑的曲線連接起來.

（學生描點、連線）

師：在畫圖過程中，我們應該注意哪些問題呢？

生1：在連點成線的過程中，應該用平滑的曲線，而不能用折線連接.

生2：所畫曲線應該在第一象限內，不能與坐標軸相交，因為F和L 的取值都是大于0的.

師：（教師用多媒體展示學生所畫圖像）這條曲線是反比例函數圖像的一支嗎？

生：3：是的.

師：你能說說你的依據嗎？

生3：結合物理學科中學習的“杠桿原理”，即F·L=F·L. 根據本題的題意，我們可以得到這樣的式子：25×9.8=F·L，進而得出：F=，而且L>0，所以這個圖像是反比例函數圖像的一支.

師：那么，（50，4.9）這個點是否在這條曲線上？說出你的理由.

生1：（50，4.9）這個點在曲線上，因為50×4.9=245，滿足F=.

教學中，教師引導學生以物理學科中的“杠桿原理”得出F=，從而建構起反比例函數圖像的模型，在這個過程中，進一步密切了數學與物理的內在聯系，培養了學生的數學建模意識和能力，有利于學生以數學的視角分析和解決具體問題.

協作解釋，深化認識

STEM教育注重學生的學習體驗，在教學中，教師可設計具有探究性的問題，組織學生自主思考、協作解釋、動手實踐，這樣不但使學生掌握了結論性知識，還使學生體驗、感悟了知識產生的過程，由此發展了學生的思考力與探究力.

【活動一】

師：以上題為例，假如我們改變重物懸掛的位置，然后重復上面的操作過程，這時我們所得到的曲線是否仍然是反比例函數的一支？（為了更加快捷地得到精準的函數圖像，教師可以指導學生運用手持圖形計算器HP39gs繪制函數圖像）

（學生以小組為單位進行探究，自由改變重物懸掛的位置，并用圖形計數器繪制圖像）

生1：改變重物懸掛位置，所得到的曲線仍然是反比例函數圖像的一支. 因為根據杠桿原理，F與L的積仍然是一個固定值.

師：點（50，4.9）還在新的函數圖像上嗎？

生1：不在. 因為50×4.9=245，而由于重物懸掛位置改變了，所以重物的質量與重物到中點O的距離之積也發生了改變（不等于245），所以點（50，4.9）不在新的函數圖像上.

教學中，通過改變重物懸掛位置，提升了實驗結果的多樣性和代表性，這有利于學生從實驗結果的變與不變中把握反比例函數的本質屬性. 除此之外，教師將信息技術融入數學學科的學習當中，通過采用圖形計算器HP39gs可以更加迅捷地繪制出精準、直觀的反比例函數圖像，體現了數學教學的跨學科性.

【活動二】

師：在繪制的所有的反比例函數中，是否存在兩個圖像相交的情形呢？你如何論證自己的觀點.

生1：從圖形計算器HP39gs繪制的圖形來看，并不存在兩個相交的圖像.

師：我們怎樣論證自己的猜想呢？

生1：盡管我們繪制了很多反比例函數圖像，但是仍然不能從正面說明這一問題，畢竟反比例函數是永遠也畫不完的.

生2：我們采用反證法證明就會簡單很多. 我的思路是這樣的：假設有兩個不同的反比例函數y=和 y=，k≠ k′，假設這兩個函數圖像相交于一點P（a，b），我們把（a，b）分別代入y=和 y=之中，就能夠得到k=ab，k′=ab，由此得出k=k′，這就與前面的條件k≠ k′相矛盾了，因此，不存在兩個相交的函數圖像.

STEM教育注重小組團隊之間的協作. 當學生在探究問題過程中陷入困境時，教師不必急于將答案和盤托出，而是要給予學生充分的合作交流的時間和空間，讓學生在相互交流中取長補短，最終順利解決問題.

【活動三】

師：反比例函數在現實生活中應用廣泛，請同學們結合自己的生活經驗，找出生活中蘊含反比例函數關系的例子.

（學生獨立思考3分鐘，然后展開討論）

生1：生活經驗告訴我們，當我們使用剪刀的時候，物體放在剪刀的不同位置，我們所用的力也是不同的，這是運用了反比例函數的原理.

生2：臺燈燈光亮度的調節也是反比例函數原理在生活中具體運用的表現. 在電壓一定的前提下，臺燈功率P是電阻R的反比例函數，電阻越小，臺燈的輸出功率越大，燈光就越亮;反過來，電阻越大，臺燈的輸出功率越小，燈光就越暗.

生3：在路程一定的前提下，物體運動速度與所需時間成反比例關系.

……

STEM教育強調學以致用，讓學生將學到的知識運用到具體的生活當中. 學生結合自己的生活經驗，列舉出反比例函數原理在現實生活中的運用，在這個過程中，構建了數學與生活的聯系，提升了數學應用意識.

反饋評價，積累經驗

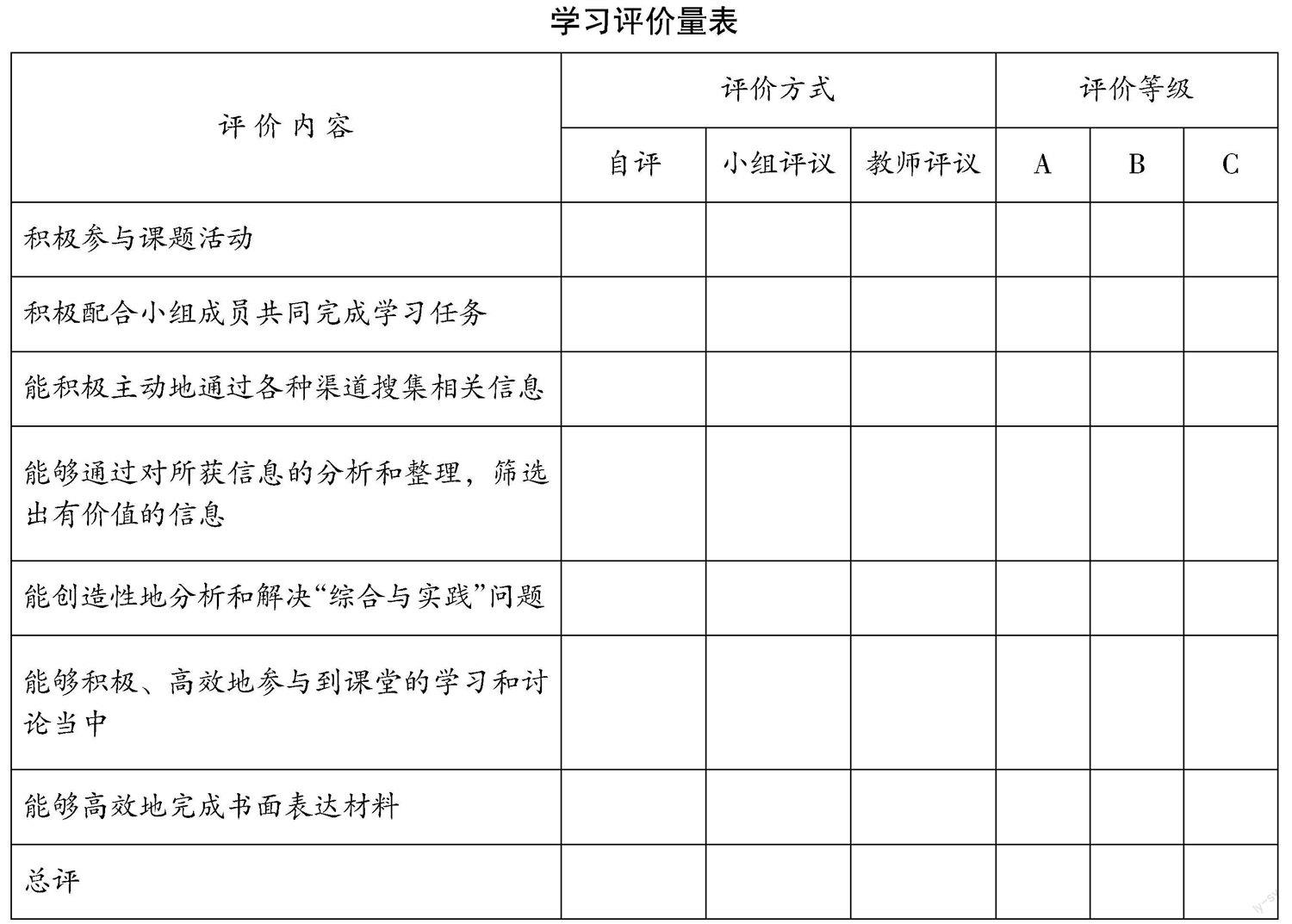
反饋評價是教學活動的重要環節. 但是，課堂評價并不僅僅是對學生的課堂表現進行鑒定，它更重要的是作為一種賞識、導向和激勵的手段，為教師的“教”和學生的“學”提供方向，注入動力. 在反饋評價環節，教師可把自評和互評相結合，把過程性評價和總結性評價相結合，審視和反思自己在學習中的成敗得失，以為今后的學習提供參考.

學生、小組長和教師按照學生表現實際情況填寫學習評價量表，在這個過程中，不僅有利于教師反思自己的教學過程，也有利于學生重新審視自己的學習過程，從而為今后“綜合與實踐”課題學習積累經驗.

總之，將STEM教育理念融入“綜合與實踐”課程當中，有利于更好地體現數學與其他相關學科的聯系，有利于學生以數學的視角分析和解決問題，有利于學生將數學知識運用到生活實踐當中，更好地體現數學學習的實用價值.

參考文獻：

[1]黃雄. 基于STEM教育理念的初中數學“綜合與實踐”課程教學研究[J]. 福建教育，2021（19）：27-29.

[2]崔競. 基于STEM理念的初中數學建模教學實踐[J]. 數學之友，2021（03）：20-22.