融合實例頻率加權正則化和神經網絡的概率矩陣分解模型

韋凱欣，宋 燕

（1上海理工大學 理學院，上海 200093；2上海理工大學 光電信息與計算機工程學院，上海 200093）

0 引 言

近年來，隨著計算機技術的全面發展，信息呈現爆炸式增長。面對這些海量數據，如何通過數據挖掘相關理論和技術手段挖掘出潛在的、有效的以及可被解釋和理解的信息，一直以來都是亟待解決的問題。矩陣分解（Matrix Factorization，MF）模型，特別是概率矩陣分解（Probabilistic Matrix Factorization，PMF）模型由于其在大規模稀疏數據集上的良好性能而被廣泛應用。通過將原始的高維數據矩陣映射到低維的潛在因子空間，來挖掘隱藏的有用信息。然而，由于天然的技術手段不足或者后期存儲設備故障等原因，數據缺失難以避免，這就造成了原始數據矩陣的高維稀疏現象。當面對大規模、不均衡稀疏數據時，PMF模型往往會出現過擬合和迭代訓練時間復雜度高等問題。

在大規模、不均衡稀疏矩陣上進行矩陣分解，本質上是一個不適定問題，難以找到唯一的或者全局最優解。正則化通常是解決上述問題，提高模型泛化能力的有效方法之一。然而，目前大部分矩陣分解的方法都采用了一般的正則化方法，如L正則化。但是，這些正則化方法通常是針對沒有缺失項的完整數據集的，高維稀疏數據集在稀疏度和數據均衡度方面都存在很大的差異，直接使用這些傳統的正則化方法取得的效果可能事倍功半。如何設計出適用于不完整數據集的正則化方案，更加準確地刻畫原始矩陣，已然成為亟待解決的重要課題。

另外，時間復雜度也是判斷一個模型性能好壞的標準之一。目前，大部分模型的求解方法，都依賴于迭代求解，如梯度下降法（Gradient Descent，GD）。其主要思想是沿著參數當前位置的負梯度方向進行迭代更新，逐步達到最優解。然而，這種訓練方法，往往需要付出巨大的時間代價，而且隨著數據集的不斷擴大，這種時間消耗更是難以忍受。不同于這些傳統的訓練方法，基于神經網絡的方法通常僅需一次迭代，可以大大提升模型的訓練效率。因此，本文將神經網絡引入到模型的訓練過程當中。

綜上所述，本文提出一種融合實例頻率加權正則化和神經網絡的概率矩陣分解模型，在提高模型預測精度的同時大大提升模型訓練效率。本文的主要貢獻如下：

（1）基于傳統的PMF模型，建立一種新的融合數據不均衡分布信息和神經網絡的概率矩陣分解模型，即IR-NNPMF模型。

（2）基于稀疏矩陣行列之間數據不均衡分布的信息，通過引入實例頻率加權的正則化方案，有效地緩解模型過擬合問題。

（3）引入神經網絡進行模型的參數訓練，整個訓練過程當中，只需要進行一次迭代，大大提高了模型的訓練效率。

（4）在4個真實的工業應用數據集上的實驗結果證明，本文提出的IR-NNPMF模型可以有效緩解模型的過擬合問題，在提升預測精度的同時減少模型的訓練時間。

1 相關工作

1.1 概率矩陣分解模型

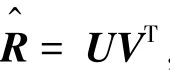
為了對模型進行學習，首先，假設已經觀測到的原始矩陣服從以下高斯分布：

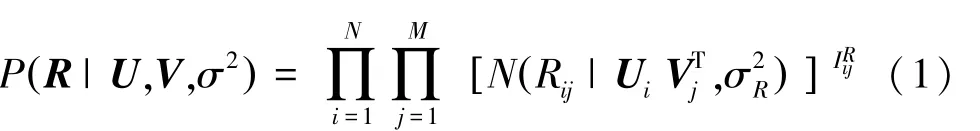
其中，(，)是均值為，方差為的高斯分布的概率密度函數；R表示位于矩陣中第行和第列的元素；U 表示位于矩陣中第行的行向量；V 表示位于矩陣中第行的行向量；I是指示函數，如果R有數據，則為1，否則為0。

為了防止過擬合，假設2個低秩矩陣的潛在因子向量服從零均值的高斯先驗分布：

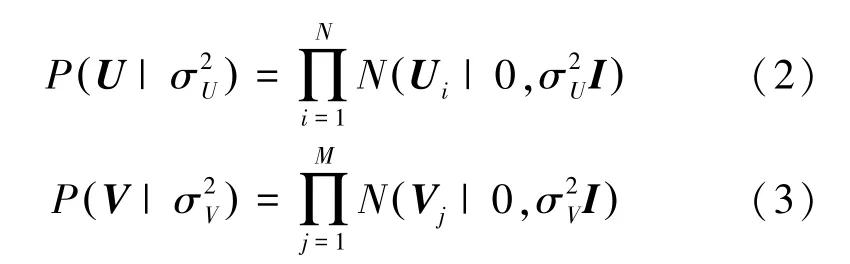
根據貝葉斯公式，可得潛在因子向量的后驗log函數：

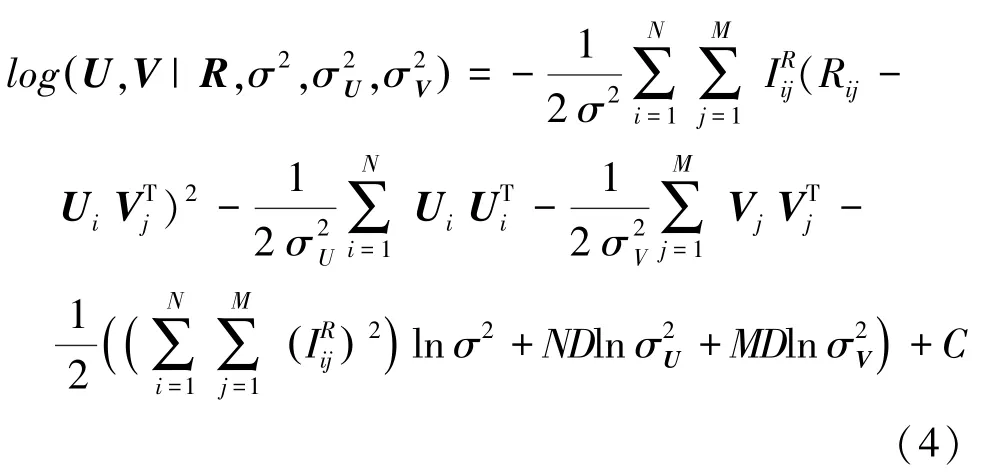
其中，是不依賴于任何參數的常量。

最大化函數等價于最小化式（5）中的目標函數，即：

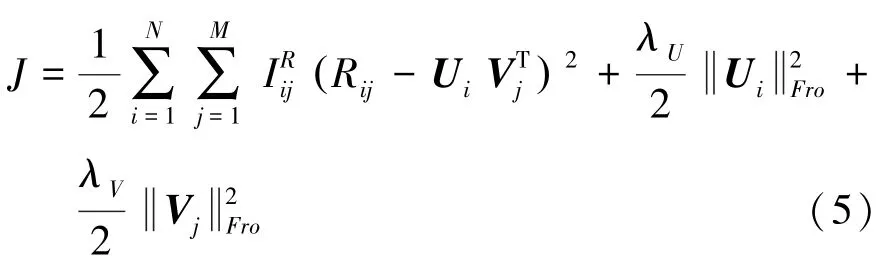
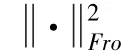
1.2 實例頻率加權正則化方案

不均衡高維稀疏數據集上的不適定問題往往嚴重依賴于最初的假設。加入正則化是解決這類問題的有效方法之一，例如正則化。式（5）的正則化方案為：

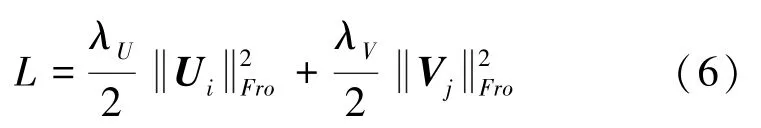
然而，這些傳統的正則化方法通常適用于完整的數據矩陣。面對高維稀疏的數據矩陣，就需要根據每行或每列不同的已知實例數，為其分配不同的正則化系數。因此，將式（6）改進為式（7）：

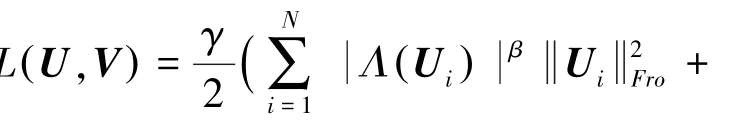
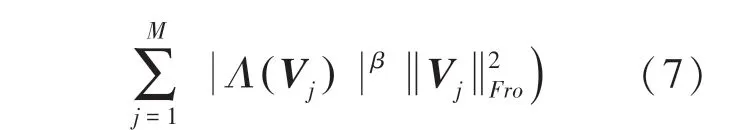
其中，(U)表示行向量U 中的已知實例的個數；(V)表示行向量V 中已知實例的個數；(x)＝表示底數為，指數為的冪函數，用來實現對正則化效果的細粒度控制。

1.3 自編碼神經網絡

自編碼神經網絡模型作為一種無監督模型，通過重構輸入信號，提取出比原始無標注數據更好的特征表述，從而取得更好的模型效果。最簡單的自編碼神經網絡包括3層：輸入層、隱藏層（也稱編碼層）和輸出層（也稱解碼層）。具體的自編碼神經網絡結構圖如圖1所示。

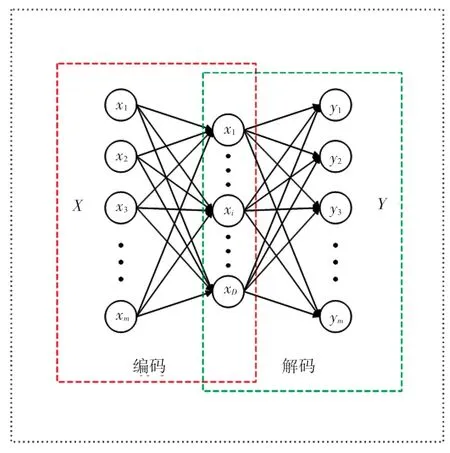
圖1 自編碼神經網絡模型Fig.1 Autoencoder Neural Network model

假設輸入層有個樣本，，…，x，隱藏層有個神經元，對應的輸出層為，，…，y。 首先，通過隱藏層將原始輸入數據映射到更低維度的空間，從而提取出重要特征。此處需用到的數學公式為：

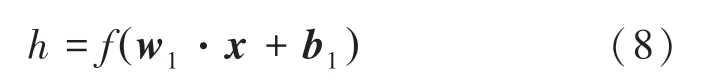
其中，是權重參數矩陣；是偏置參數向量；是激活函數，例如()1(1exp())。

其次，再通過輸出層重構這些重要特征。相應的數學公式可表示為：

其中，是權重參數矩陣；是偏置參數向量；同樣是激活函數。為了能更好地表述原始數據，輸出層通常與輸入層的維度一致。

最后，構建從輸入層到輸出層的代價函數，并最小化代價函數得到最優特征表述。由此推得的數學公式為：

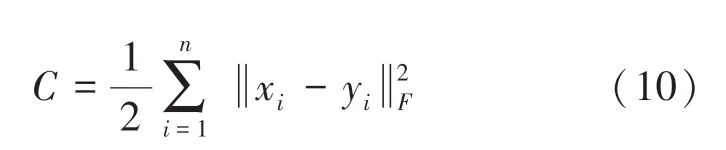
其中，表示輸入層樣本的個數。

2 主要結果

2.1 IR-NNPMF模型

面對大規模稀疏數據集上的數據不均衡分布現象，傳統的正則化方法取得的效果并不理想。因此，本文創造性地提出一種融合實例頻率加權正則化和神經網絡的PMF模型，即IR-NNPMF模型。具體的模型結構圖如圖2所示。

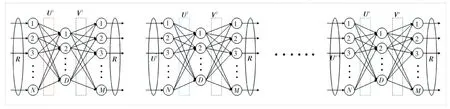
圖2 IR-NNPMF模型結構圖Fig.2 Structure of an IR-NNPMF model

本文將與潛在因子有關的實例頻率融入到正則化項當中，故對傳統PMF模型當中的潛在因子的先驗分布條件進行改進，具體如下所示：

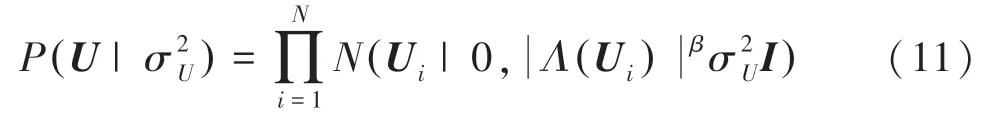
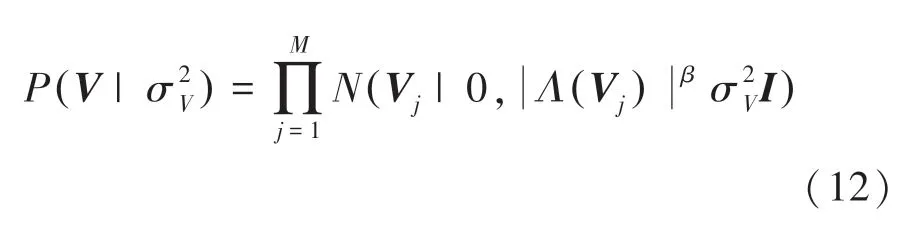
潛在因子的對數后驗分布函數如式（13）所示：

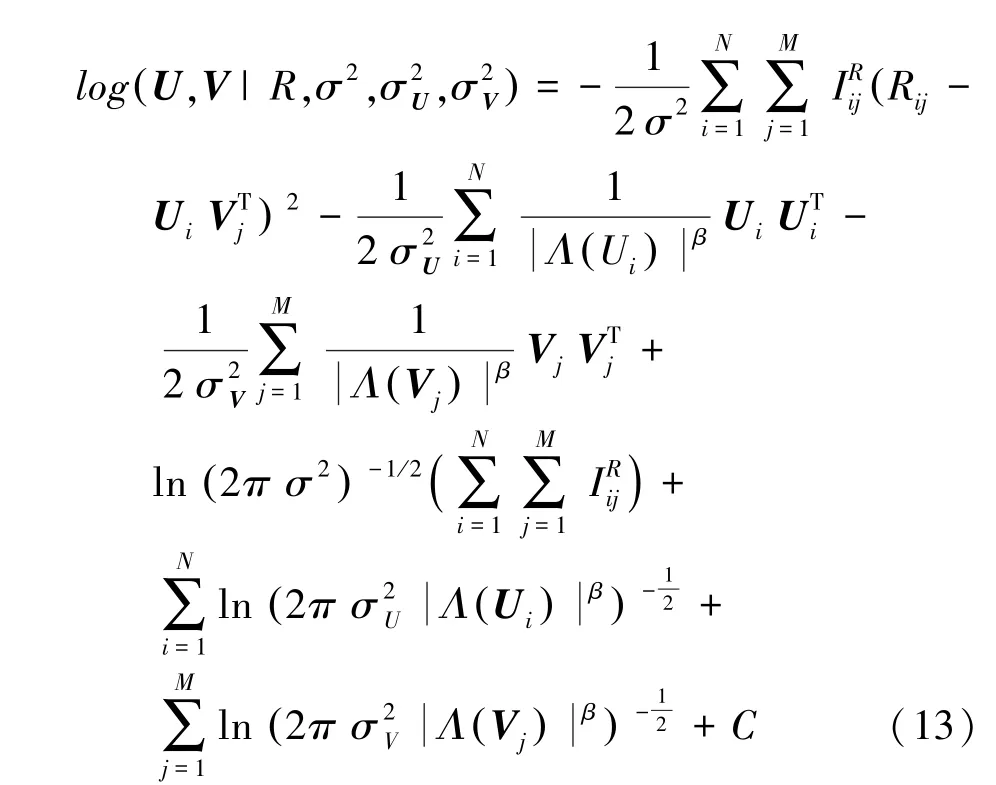
最終的目標函數可表示為：

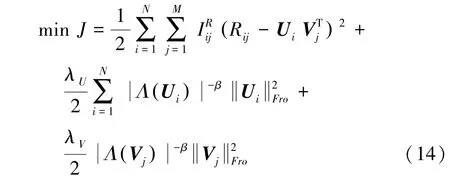
2.2 基于神經網絡進行參數訓練

本文引入神經網絡進行參數訓練，提高模型的訓練效率。假設IR-NNPMF模型包含層神經網絡，研究展開的模型訓練過程為：

（1）當1時，即模型包含一層神經網絡。將矩陣的每一行輸入到輸入層，并分別通過潛在因子矩陣和對輸入數據進行編碼和解碼。

（2）當≥2時，即模型包含多層神經網絡。對于第一層神經網絡，其訓練過程和單層神經網絡模型相同；在第2層及之后的訓練過程中，將上一層輸出的潛在因子矩陣U 的每一行向量作為輸入數據，進行當前層的U 的訓練。

緊接著，將對模型參數U 和V 進行求解。

（1）當1時。研發求解過程如下。

首先，初始化潛在因子矩陣。將原始矩陣進行輸入，然后通過隨機學習算法得到權重矩陣W 和偏置向量，之后首次更新：

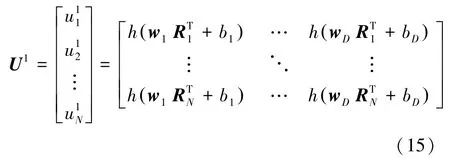
其中，，，…，w 表示權重矩陣W 的每一行元素；，，…，b表示偏置向量的每一個元素。

其次，更新潛在因子矩陣。 具體做法如下：

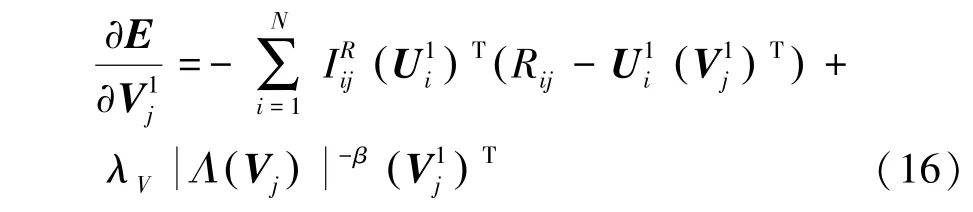
①計算中每一個行向量的偏導數：

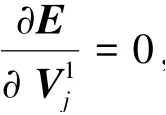
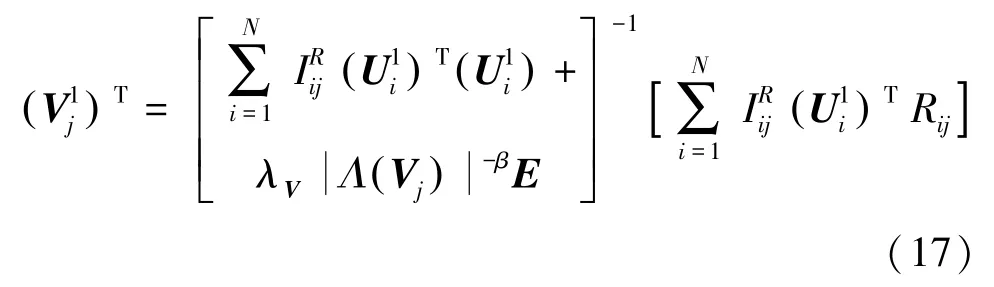
其中，表示一個維度為的單位矩陣。

最后，再次更新潛在因子矩陣。首次更新的是通過隨機學習算法和神經網絡得到的，具有一定的隨機性。為了更好地近似矩陣，根據更新過的，再次更新，其方法與更新類似：

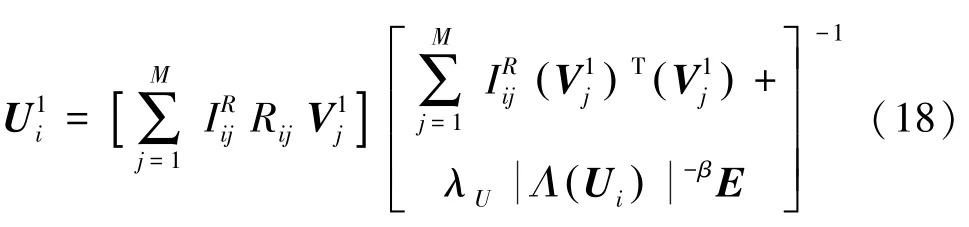
（2）當≥2時。從圖2可以看出，與單層神經網絡最大的不同之處在于，模型當前層的輸入數據是上一層的潛在因子矩陣U 。 其訓練過程與單層神經網絡類似，具體如下。

首先，初始化潛在因子矩陣U 。 研究后可得：

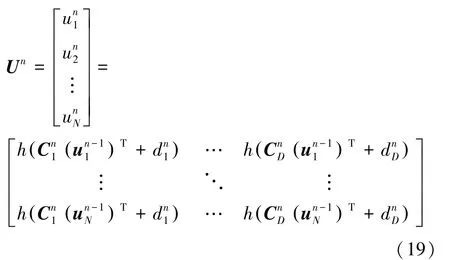
其中，C，C，…，C表示第層神經網絡權重矩陣C ∈?中每一行元素；d，d，…，d表示第層神經網絡偏置向量d∈中每一個元素。

其次，更新潛在因子矩陣V 。 研究后可得：

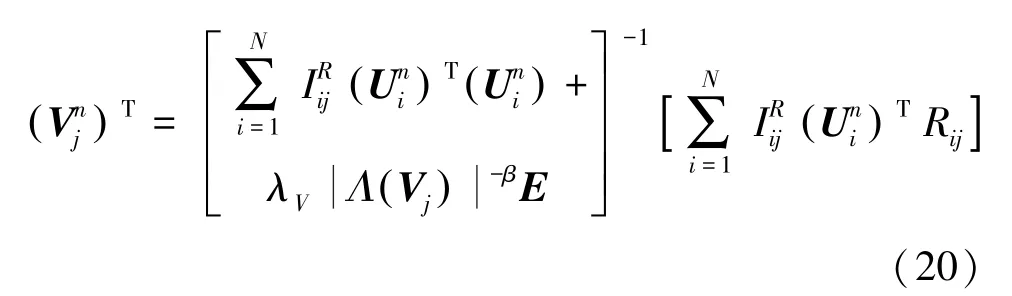
最后，再次更新潛在因子矩陣U 。 研究后可推得：

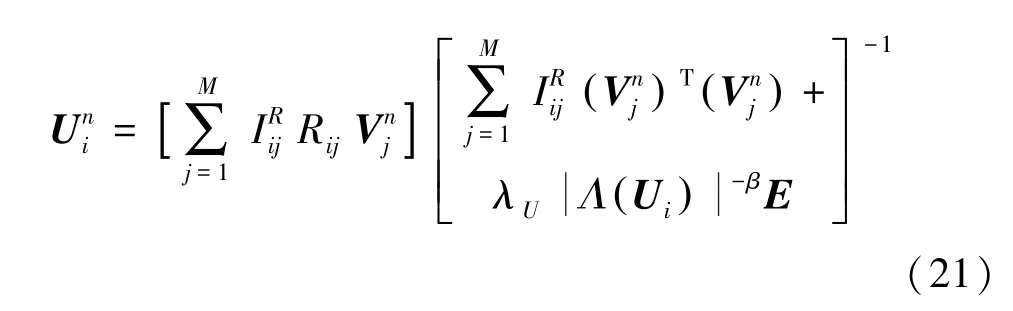
2.3 算法設計和復雜度分析

針對2.2節中參數更新步驟，研究設計了IRNNPMF模型的算法流程，算法代碼詳見如下。

已知數據集合，，，正則化系數λ和λ

因子矩陣U ，V

當1時，根據式（15）求解因子矩陣，當≥2時，根據式（19）求解因子矩陣U 。

根據式（20）求解因子矩陣V 。

根據式（21）更新因子矩陣U 。

該算法的主要時間消耗是計算參數更新公式（20）、（21）中的逆矩陣，其時間復雜度為)，其中是潛在因子空間的維度。也就是說，越小，模型訓練所花費的時間越少。然而，過小的話，不能很好地表述原來矩陣的特征。因此，在實驗過程當中，往往需要取一個合適的值來平衡模型的特征表述和時間復雜度。

此外，神經網絡層數的取值也至關重要。越大，訓練模型所需要的時間就越長；過小，模型的預測精度就達不到要求。因此，在實驗過程當中也需要設置一個合理的取值。

3 實驗結果與分析

3.1 評估指標

本文使用均方根誤差（Root Mean Square Error，）和平均絕對誤差（Mean Absolute Error，）作為實驗評估標準，具體公式為：

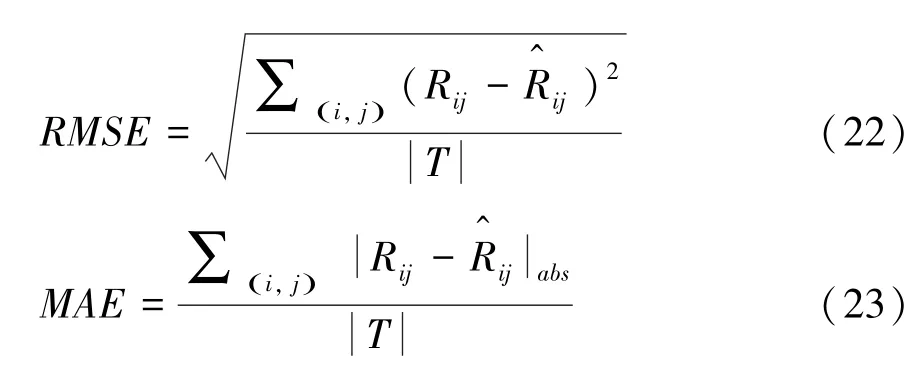
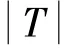
3.2 實驗數據集及預處理

本文選取了4個真實工業應用數據集作為實驗數據集來驗證所提出模型的性能。數據集信息見表1。

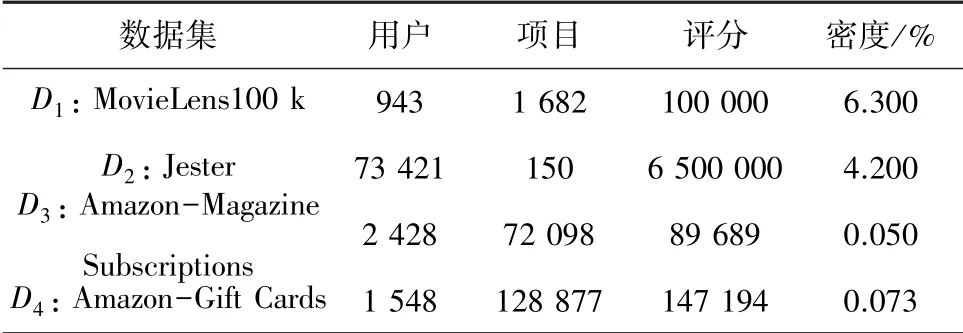
表1 數據集信息Tab.1 Information of datasets

為了避免模型訓練受到其他因素的影響，本文將所有數據集進行歸一化處理；并將所有數據集按照8：2劃分訓練集和測試集，且在訓練集上進行5折交叉驗證；最后進行10次獨立重復實驗，取其平均值作為最終的實驗結果。以上所有實驗都是用Pycharm實現，在Intel Core i5 CPU 1.40 GHz，8 GB內存和AMD Ryzen 7 3700X CPU 3.58 GHz，32 GB內存的計算機上運行。

3.3 實驗對比模型設置

為了體現本文提出模型的優越性，這里將與數個模型進行對比。各對比模型信息參見表2。

表2 對比模型信息Tab.2 Information of compared models

3.4 模型參數設置

在進行對比實驗前，需要對模型的參數進行靈敏度測試，并設置最優參數。為了減小模型的復雜度，所有模型中的正則化系數λ和λ設置為λ＝λ＝λ。 因此，這里需要對以下參數進行訓練：正則化系數，正則化實例頻率加權指數，潛在因子維度，神經網絡層數，具體訓練過程如圖3～圖7所示。

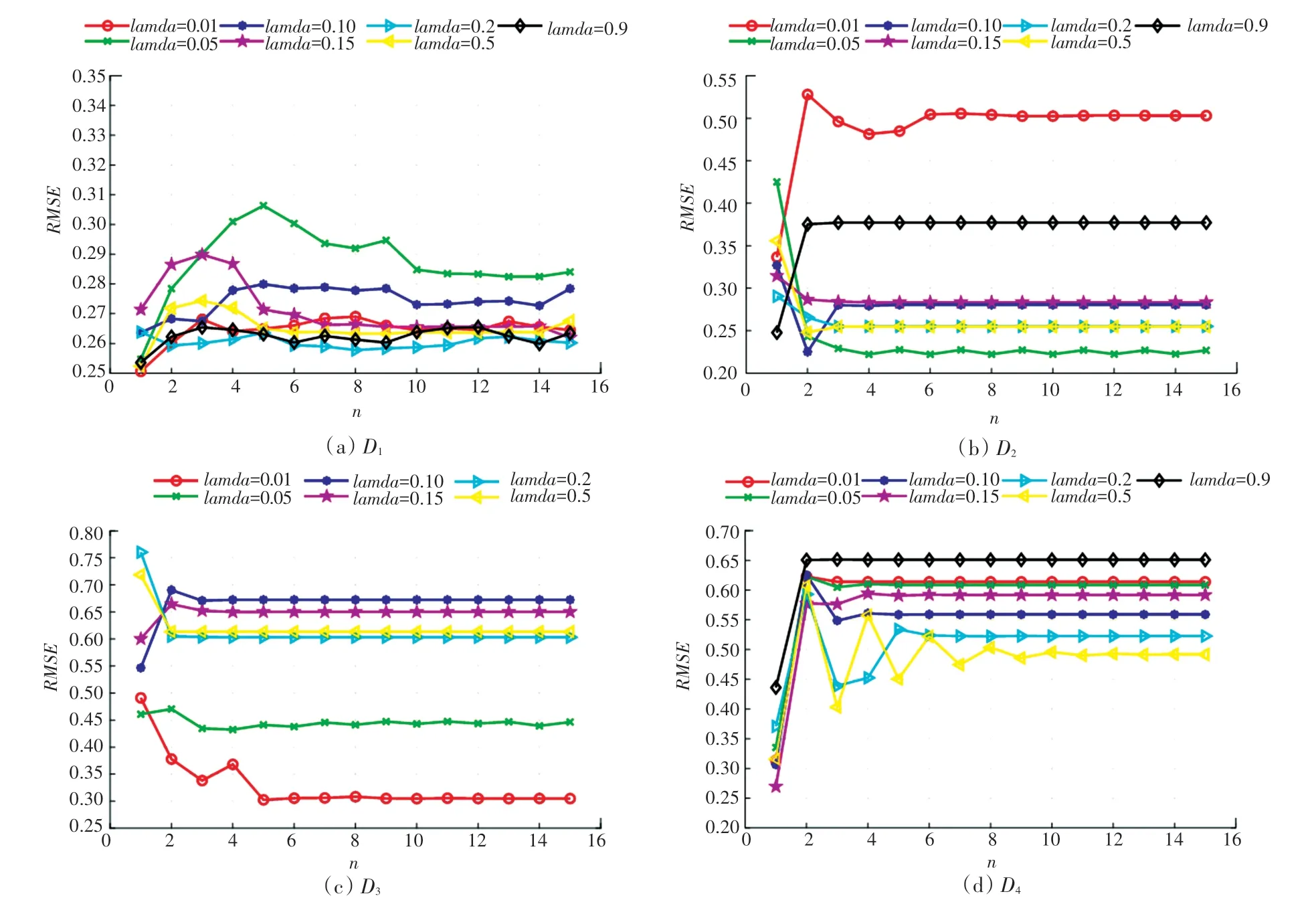
圖3 正則化系數λ對RMSE的影響Fig.3 Influence of regularization coefficientλon RMSE

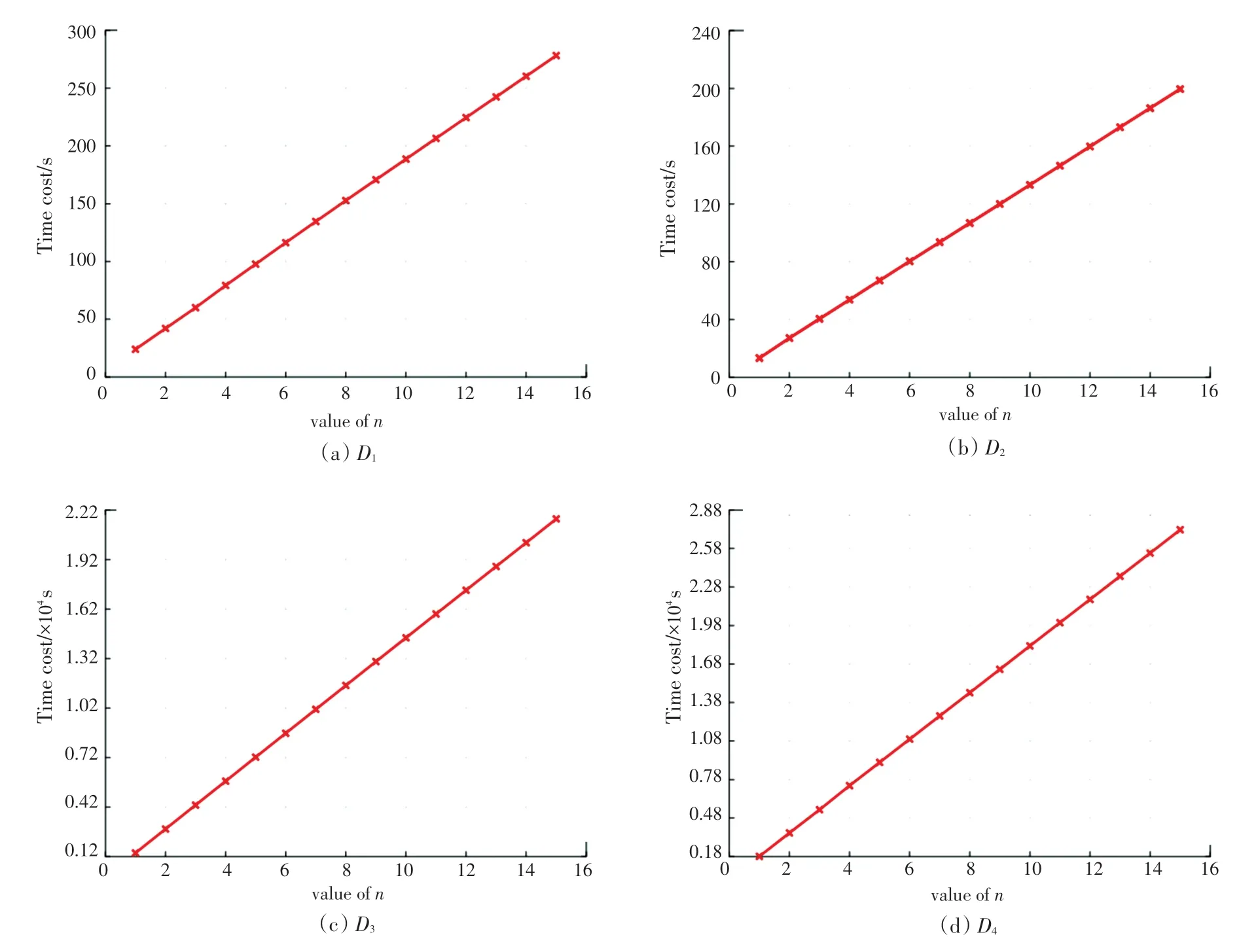
圖7 不同神經網絡層數n的時間花費Fig.7 Time costs with different layers of neural networks

圖3 展示了正則化系數對模型性能的影響，其中圖3（a）～（d）分別表示模型在數據集上的參數靈敏度測試結果。可以發現，當正則化實例頻率加權指數和潛在因子維度固定的情況下，不同數據集的最優正則化參數是不同的。即上的最優參數分別為0.2，0.05，0.01，0.5。

圖4展示了正則化實例頻率加權指數對模型性能的影響，其中圖4（a）～（d）分別表示模型在數據集上的參數靈敏度測試結果。可以發現，當正則化系數和潛在因子維度固定的情況下，數據集的最優正則化實例權重指數分別為1.0，0.6，0.8，1.0。

圖4 正則化實例權重指數β對RMSE的影響Fig.4 Influence of regularization instance-frequency weight indexβon RMSE

圖5展示了不同神經網絡層數下潛在因子維度對模型性能的影響，其中圖5（a）～（d）分別表示模型在數據集上的參數靈敏度測試結果。可以發現，不同數據集上最優的潛在因子維度是不同的。具體地，在、和上，很容易得出最優的值為10，20，10；但是，在上，從20增加到160對模型精度的影響不明顯。當神經網絡層數6時，和20相比，160時，僅降低了0.005 02，考慮到越大，時間復雜度越大，這里選擇20作為最優參數。

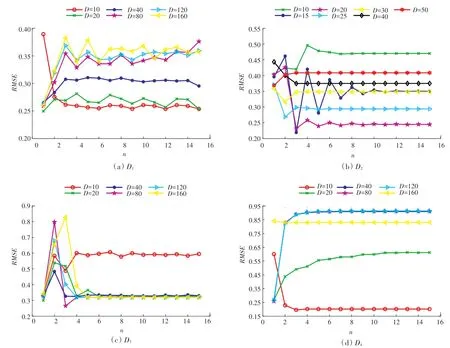
圖5 潛在因子維數D對RMSE的影響Fig.5 Influence of latent factor dimension D on RMSE

模型參數的設置，除了要對比預測精度外，還要衡量不同參數下的模型訓練時間。圖6、圖7分別展示了在不同潛在因子維度和神經網絡層數下的時間消耗。從圖6、圖7中可以看出，不管在哪個數據集上，隨著和的增加，模型的訓練時間都會迅速增加。例如，從圖6（c）中，可以看出在數據集上，當20時，模型的訓練時間為21 742.329 84 s，而160時，模型的訓練時間為41 035.049 28 s，增加了88.73%。雖然隨著的增加，模型的表征擬合能力會大大增加，但是所帶來的巨大的時間代價，也是難以忍受的。因此選擇合適的值是十分重要的。

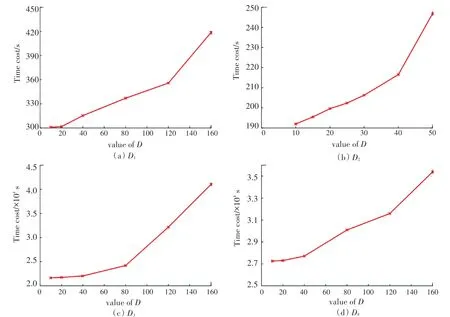
圖6 不同潛在因子維數D的時間花費Fig.6 Time costs with different latent factor dimension D

同樣地，從圖7（c）中可以得到，在數據集上，當5時，訓練時間為7 222.471 204 s，而當15時，訓練時間迅速增加到21 656.375 45 s。雖然，經過訓練的神經網絡層數越多，越能更好地擬合原始數據矩陣，但是帶來的時間消耗也是巨大的。因此，選擇合適的值也是十分必要的。

經過上述分析，研究得到IR-NNPMF模型在不同數據集上的參數設置為：在上，02，08，10，2；在上，005，06，20，4；在上，001，08，20，6；在上，05，10，10，4。

3.5 實驗結果分析

最后為了評估本文提出模型的有效性，對3.3節中所提出的3個模型進行對比實驗。為了得到一個無偏的結果，和在4個數據集上參數設置如下：

對于模型，正則化系數，正則化實例頻率加權指數和潛在因子維度，分別與模型在各個數據集上的取值相同，并在各個數據集上對學習率在［0000 1，0001，001，005，01，05，09］內進行靈敏度測試，最終數據集的最優參數分別為：0.000 1，0.000 1，0.5，0.1。對于模型，潛在因子維度和學習率，分別與在各個數據集上的取值相同，并在各個數據集上對正則化系數在［0000 1，0001，001，005，01，05，09］內 進行參數靈敏度測試，最終數據集的最優參數分別為：0.05，0.05，0.001，0.001。

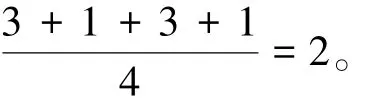
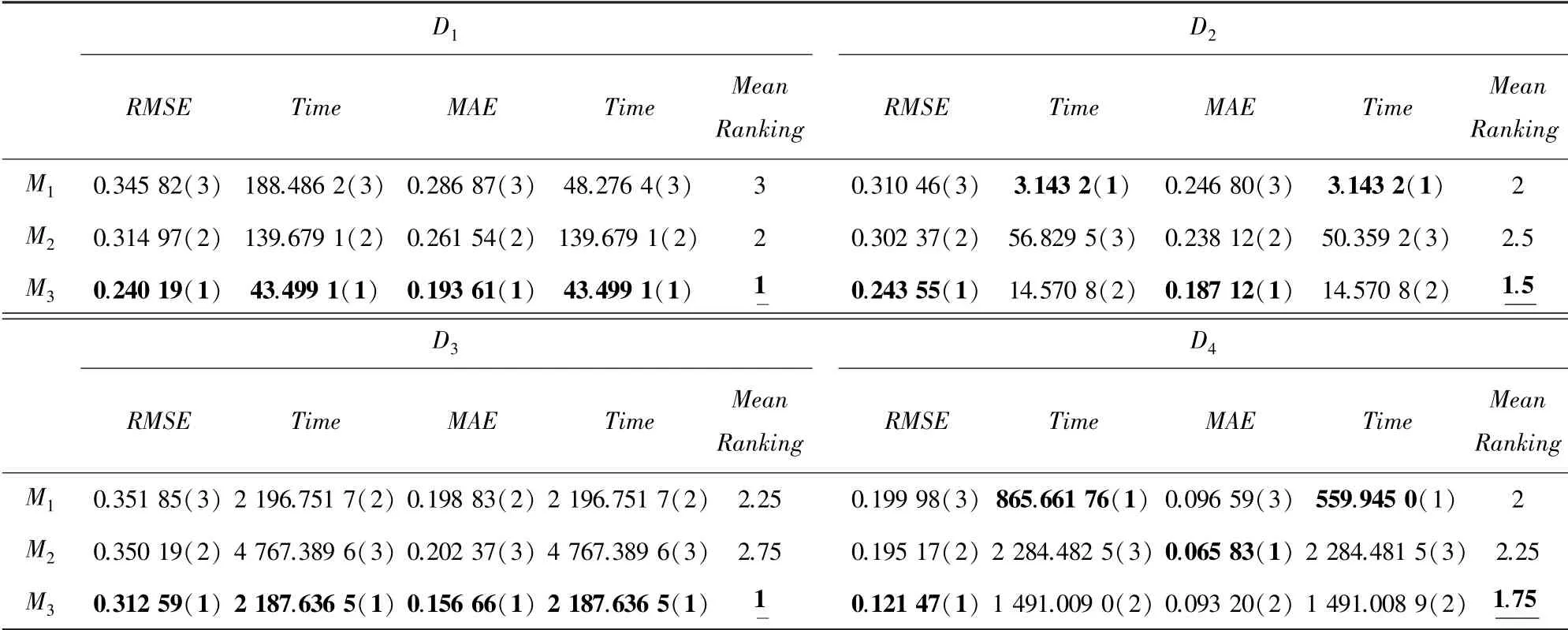
表3 模型M 1～M 3在D1～D4的最小預測誤差和相應時間開銷Tab.3 Lowest prediction error achieved by models M 1～M 3 and the corresponding time costs on D1～D4

（1）模型在數據集上關于評價指標和的性能都明顯優于模型和。例如，在數據集上，模型和取得的最小的分別為0351 85和0350 19，而模型最小的為0312 59，分別提升了112和107。模型在數據集上關于評價指標的性能均優于模型，例如，在數據集上模型取得的最小為0345 82，而模型取得的最小為0314 97，提升了89。這說明將數據的不均衡分布信息引入到正則化當中，能有效提高模型的預測精度。

（2）模型在所有數據集上的時間消耗都明顯小于模型。例如，在數據集上，模型取得的最小的時所花費的時間為4 767389 6 s；而模型所取得最小時花費的時間為2 187636 5 s。 這說明引入神經網絡能有效減少模型迭代訓練所造成的時間花費。

（3）模型在所有數據集上的綜合排名明顯優于其他對比模型，說明模型能夠在保證訓練時間的同時大大提高預測精度。綜上，在同時考慮預測精度和訓練時間這2個評價指標的情況下，模型的性能優于其他對比模型。

4 結束語

如何有效進行缺失數據的估計一直以來就是數據挖掘領域的研究熱點。本文著重考慮模型的預測精度和訓練時間兩個指標，一方面將數據不均衡信息引入到正則化當中，提高模型的泛化能力；另一方面，引入神經網絡進行模型參數的訓練，加快了模型的訓練速度，并合理地設置模型的參數，在提高模型預測精度的同時減少模型訓練時間。最后，在4個真實數據集上的實驗結果證明，本文提出的IRNNPMF模型在大型稀疏數據集上的性能是優于其他PMF模型的。