融合鯨魚泡泡網機制的SSA算法

冉 琳，潘大志，馮世強

（西華師范大學 數學與信息學院，四川 南充 637009）

0 引 言

受大自然的啟發，群智能優化算法（Intelligence Optimization Algorithm，IOA）一般是通過對自然界中各種生物的進化過程與物理現象進行研究而形成的一種迭代尋優搜索算法。近年來，涌現了一些新的群智能優化算法，比如：蛾群算法（moth swarm algorithm，MSA）、哈里斯鷹優化算法（harris hawks optimization，HHO）、布 谷 鳥 搜 索 算 法（cukoo search algorithm，CSA）、螢 火 蟲 算 法（firefly algorithm，FA）、蝙蝠算法（bat algorithm，BA）等。麻雀搜索算法是受自然界中麻雀搜索食物與反捕食行為的啟發，于2019年由薛建凱提出。為使麻雀搜索算法尋優效果更好，學者們主要通過2個方面對其進行改進。一方面，根據麻雀搜索算法本身的特性進行改進；另一方面，通過將2種或多種智能算法與麻雀搜索算法進行融合，從而達到改進SSA算法的目的。目前，已有許多學者對麻雀搜索算法展開了進一步的研究：王海瑞等人將Levy飛行策略和柯西高斯變異引入麻雀搜索算法，增加算法搜索方向的多樣性，同時也加強了局部搜索能力；呂鑫等人將高斯變異方法引入SSA算法，提高了搜索精度以及加強了算法跳出局部的能力；柳長安等人利用螢火蟲機制，對最優解進行擾動變異，從而增加種群多樣性；湯安迪等人通過引入正余弦算法和線性遞減策略，協調局部和全局搜索能力；李敦橋將模擬退火算法的Metropolis準則融入SSA算法中，使算法跳出局部最優。針對麻雀搜索算法迭代過程中，種群多樣性減少，以及容易陷入局部最優解等缺點，本文根據Tent混沌映射初始化麻雀種群，增加種群多樣性，融合鯨魚優化算法中的鯨魚泡泡網捕食數學模型，在搜索過程中，更新麻雀種群中發現者的位置，最后按自適應分布變異方式，加強了算法跳出局部的能力。

1 麻雀搜索算法

在麻雀種群中，麻雀分為發現者、加入者和警戒者三種類型。其中，發現者引導種群覓食，加入者通過發現者得到食物，發現者和加入者都有可能是警戒者。

在麻雀搜索算法（SSA）算法中，麻雀個體的適應度值決定能源高低，發現者具有較多能源，引領加入者搜尋食物。發現者有如下位置更新：

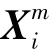
發現者與加入者的身份可以根據擁有能源的多少而改變，但每種類型麻雀的占比不變。加入者的位置更新公式為：

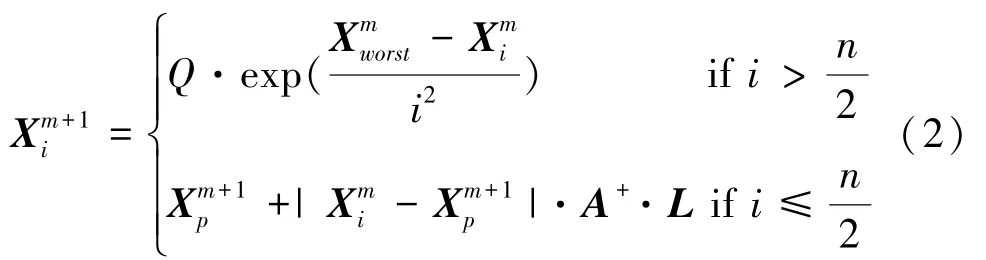
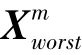
警戒者由整個種群隨機產生10%到20%，位置更新的數學表達式：

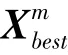
2 改進麻雀算法

2.1 Tent混沌映射

基本SSA算法利用隨機初始化種群，這種方法會導致迭代過程中種群多樣性減少。由于混沌映射具有全局遍歷性、容易實現和隨機性等特點，故本文采用基于Tent混沌映射初始化種群，以提高種群多樣性和麻雀搜索的遍歷性。Tent映射數學公式如下：

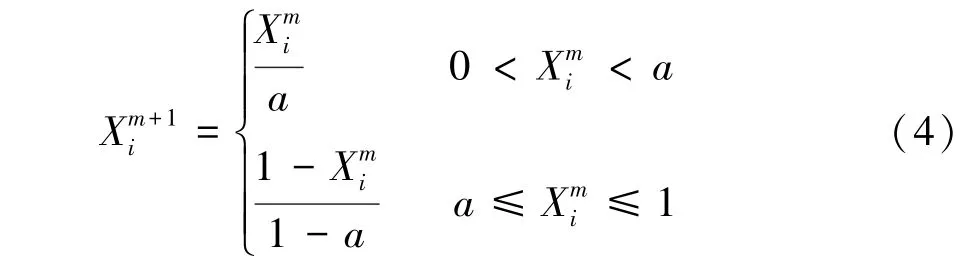
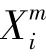
2.2 基于鯨魚泡泡網捕食機制更新麻雀發現者位置

鯨魚優化算法（Whale Optimization Algorithm，WOA）是近幾年來群智能優化算法中出現的一種新算法，本文結合WOA算法中泡泡網捕食中的收縮包圍機制和螺旋式位置更新機制，用以更新麻雀發現者的位置，以提高SSA算法的全局搜索能力。

融合后的麻雀發現者的更新位置公式為：

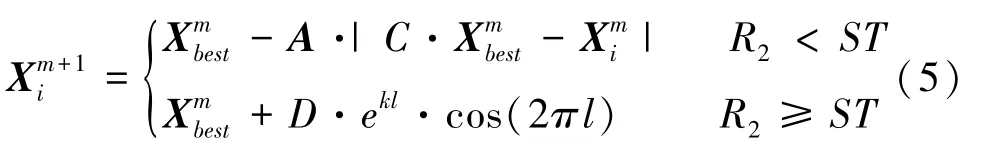
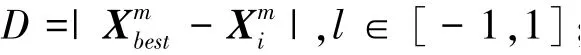
2.3 自適應t分布變異

分布的曲線形態與自由度參數的大小有關。當1時，分布是標準的柯西分布；當→∞時，分布是標準的高斯分布。分布的概率密度函數為：

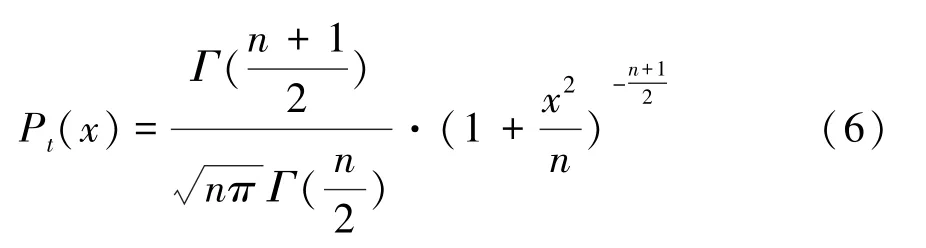
在算法的初始階段，分布近似于柯西分布變異，此時分布的全局搜索能力較強；在算法運行中期，分布變異逐漸由柯西分布變異向高斯分布變異過渡，提高了算法平衡全局搜索與局部開發的能力；在算法運行的后期階段，由于→∞，分布近似于高斯分布，此時分布的局部開發能力較強。

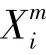
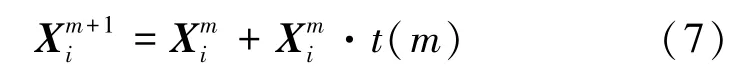
其中，X 表示分布變異后的麻雀個體位置，（）表示基于迭代次數為參數的分布。

2.4 改進麻雀算法

針對麻雀優化算法的不足，首先利用Tent混沌映射初始化種群，提高初始解的質量；在改進麻雀算法（WSSA）中，為提高尋優效果，利用鯨魚泡泡網機制擾動發現者位置更新，使得改進后算法更有利于平衡局部開發和全局搜索；最后，利用自適應分布變異更新位置，提高算法跳出局部最優的能力。具體實現步驟如下：

設置參數，預警值、發現者比例、意識到危險麻雀的比重。

基于Tent混沌映射初始化種群。

計算麻雀個體適應度值并排序。

利用式（5）更新麻雀發現者位置。

利用式（2）對加入者位置進行更新。

利用式（3）對警戒者位置進行更新。

對種群中的越界個體做越界處理。若新適應度值優于舊值，則更新位置和適應度值，反之保留。

利用式（7）對麻雀個體的位置進行分布變異，對越界個體做越界處理，并更新麻雀個體位置、適應度值以及對適應度值排序。

判斷當前迭代次數是否達到，若已達到，則循環結束并輸出結果，反之返回Step 3。

3 實驗與仿真

3.1 標準測試函數

表1分別給出了標準測試函數的公式、維數以及搜索區間。這些標準測試函數被用于測試算法的可行性、穩定性。

表1 標準測試函數Tab.1 Standard test functions

3.2 參數設置

在本文中，將各個算法的最大迭代次數設置為1 000，種群規模設定為100，即100。在灰狼優化算法（Grey Wolf Optimizer，GWO）中，是從2線性遞減至0，∈［0，1］，∈［0，1］；將引力搜索算法（Gravitation Search Algorithm，GSA）的參數設置為100，20；將麻雀搜索算法（Sparrow Search Algorithm，SSA）以及本文的改進麻雀算法（WSSA）的參數設置為：發現者占麻雀種群的0.2，警戒者占0.1，安全閾值0.8。避免程序運行一次出現誤差，本文在實驗仿真階段運行30次來獲得標準測試函數的最優值、均值以及標準差，以反映算法的收斂性、精確度和穩定性。

實驗環境：Windows 10，CPU為Intel（R）Core（TM）i5-10210U CPU＠1.60 GHz 2.11 GHz，內存16 G，Matlab 2018a。

3.3 與其他算法對比

因為單峰測試函數有且僅有一個全局最優解，并沒有局部最優解，故用單峰測試函數檢驗算法的局部開發能力。與單峰測試函數不同的是，多峰測試函數具有多個局部極值點，搜索全局最優值的難度較大，但是能夠測試出算法的搜索能力。表2給出了引力搜索算法（GSA）、灰狼優化算法（GWO）、哈里斯鷹算法（HHO）、麻雀搜索算法（SSA）以及本文的改進麻雀搜索算法（WSSA），在獨立運行了30次后的實驗結果。圖1～圖8則分別給出了在測試函數上5種算法的收斂曲線。

圖8 函數f8的對比曲線Fig.8 Comparison curve of function f8

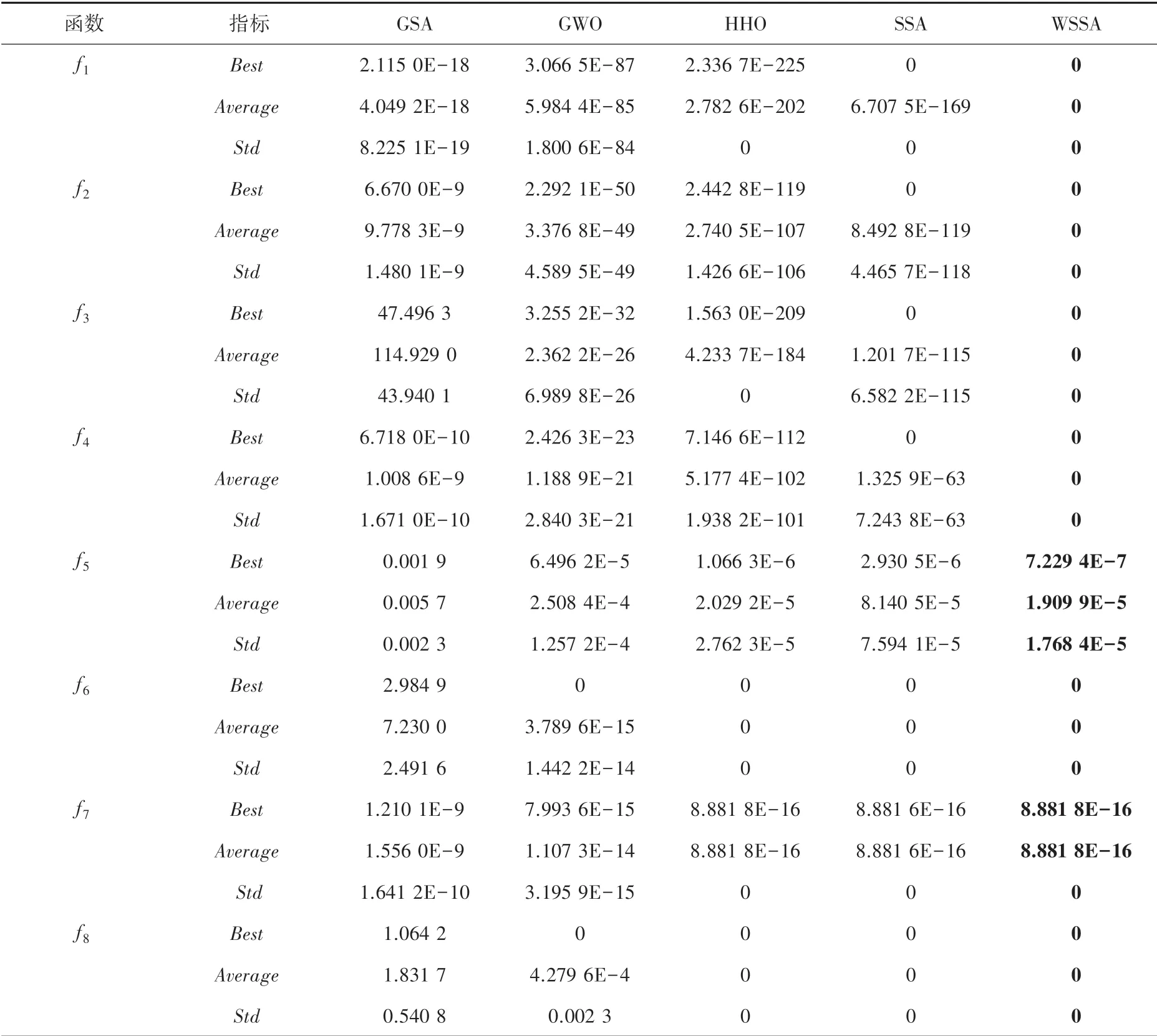
表2 測試函數優化結果Tab.2 Test function optimization results

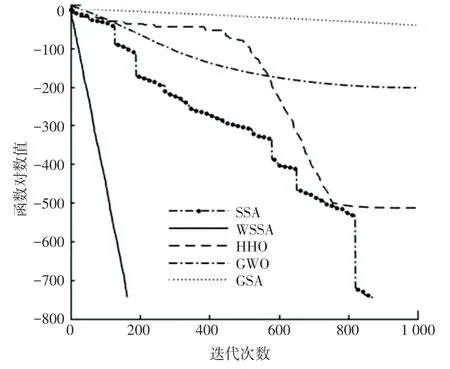
圖1 函數f1的對比曲線Fig.1 Comparison curve of function f1

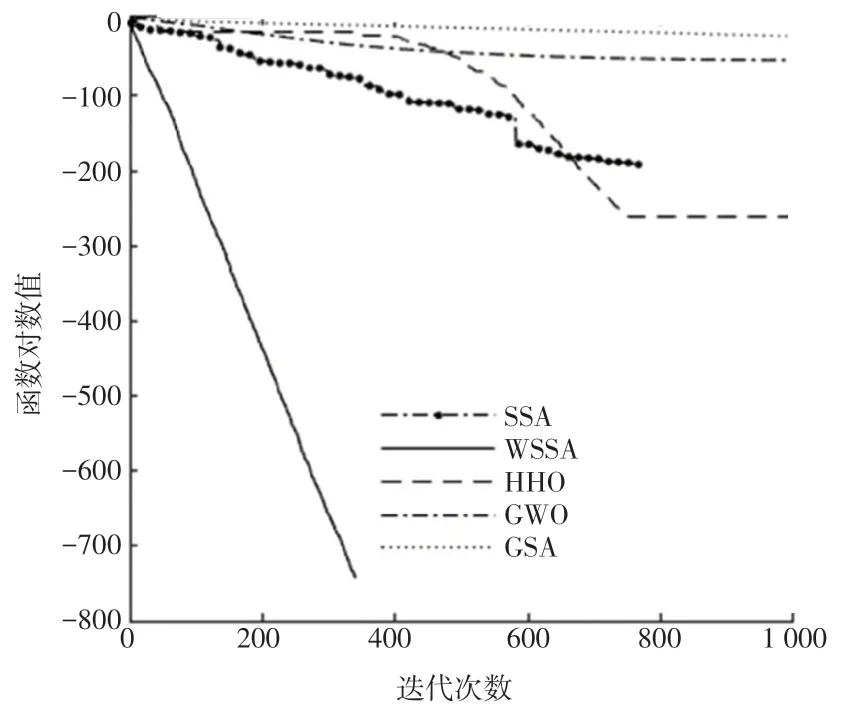
圖2 函數f2的對比曲線Fig.2 Comparison curve of function f2

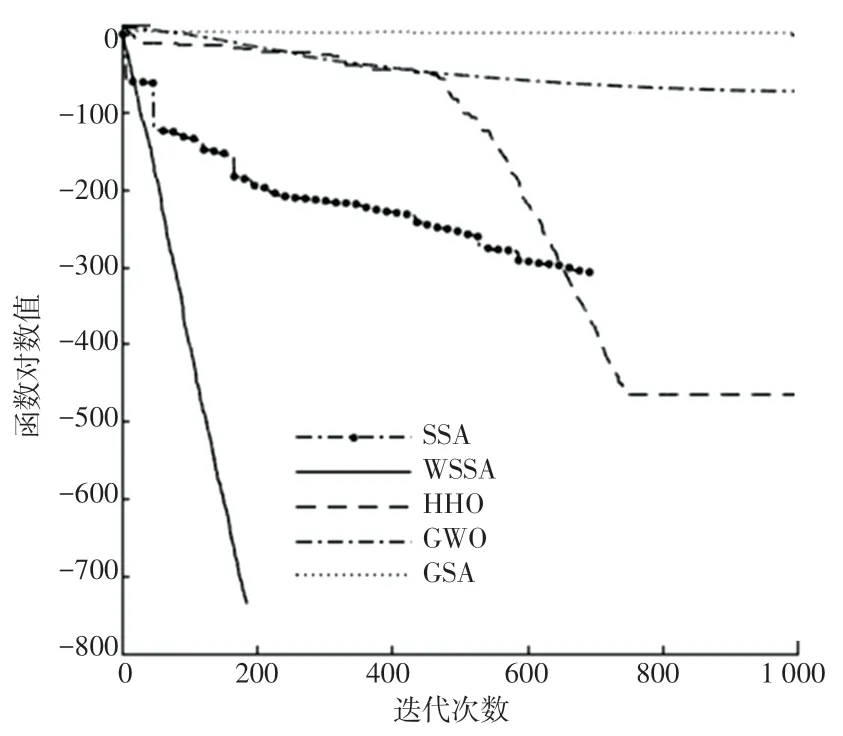
圖3 函數f3的對比曲線Fig.3 Comparison curve of function f3

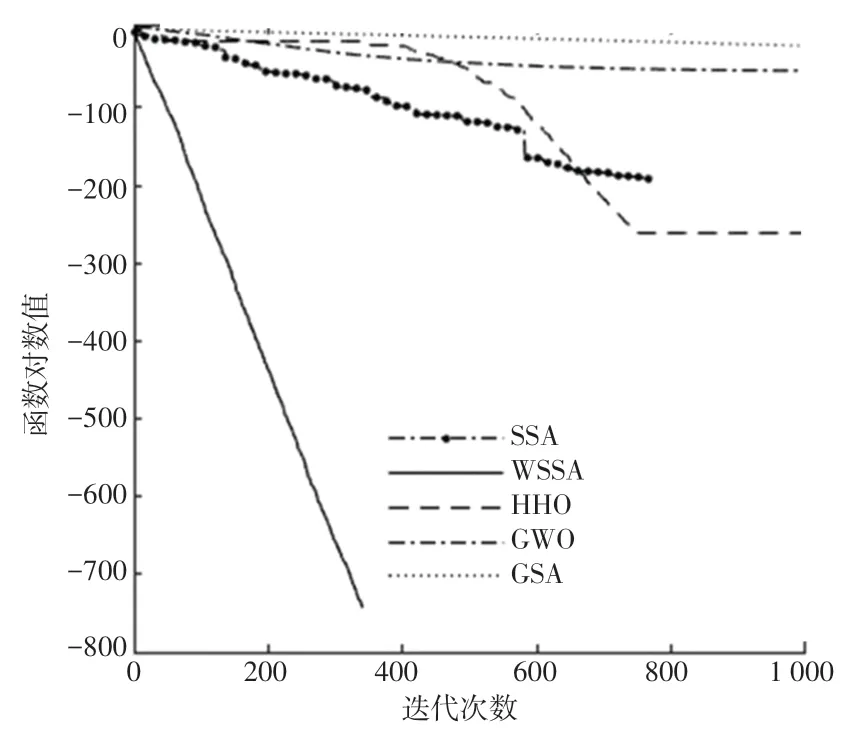
圖4 函數f4的對比曲線Fig.4 Comparison curve of function f4

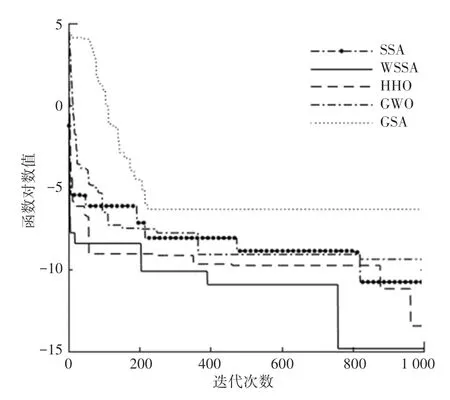
圖5 函數f5的對比曲線Fig.5 Comparison curve of function f5

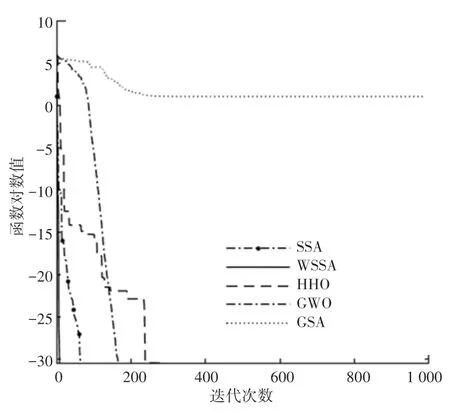
圖6 函數f6的對比曲線Fig.6 Comparison curve of function f6

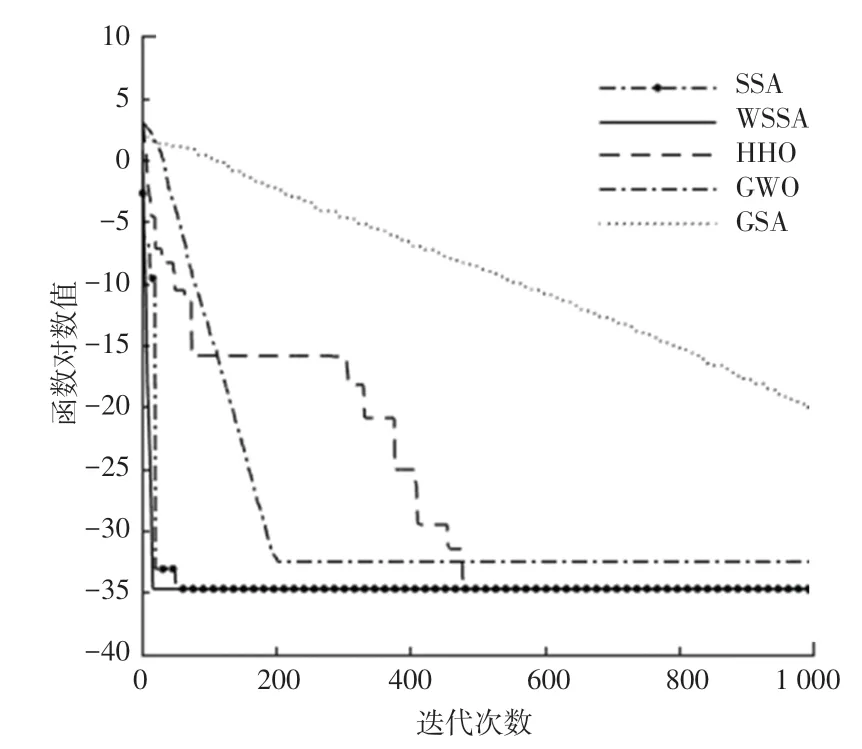
圖7 函數f7的對比曲線Fig.7 Comparison curve of function f7

3.4 結果分析

表2中給出了灰狼優化算法（GWO）、引力搜索算法（GSA）、麻雀搜索算法（SSA）、哈里斯鷹算法（HHO）以及本文的改進麻雀搜索算法（WSSA），對于8個標準測試函數在獨立運行了30次后的優化結果，、、分別表示運行30次后所得到的最優解、均值以及標準差，最優解在表2中已加粗。

從表2可以得出，引力搜索算法（GSA）的解的質量較差，灰狼優化算法（GWO）對于函數、可獲得最優解，就收斂速度而言，GWO算法對于函數、、，優于HHO算法和GSA算法，次于SSA算法和WSSA算法。哈里斯鷹算法（HHO）相較于GSA算法、GWO算法的尋優結果更好，對于函數，HHO算法尋優結果比SSA算法的好，說明此時HHO算法的局部開發能力更優，且對于函數，雖然HHO算法的收斂速度次于SSA算法和WSSA算法，但也能搜索到最優解。SSA算法相比于GSA算法、GWO算法和HHO算法，總體來說，收斂速度更快、尋優結果更好，這說明SSA算法在跳出局部極值點和全局搜索能力方面都要強于GWO算法、GSA算法和HHO算法。WSSA算法對于函數，成功地找到了全局最優解，且最優解、最優解均值、標準差都比GSA算法、GWO算法、HHO算法以及SSA算法好，表現出了很好的平衡局部與全局、跳出局部極值的能力。

為說明算法的收斂性，圖1～圖8中給出了5種算法對于標準測試函數在獨立運行30次后所得最優結果的收斂性能對比圖。在基本麻雀搜索的基礎上，因為改變了麻雀發現者的位置更新和加入了自適應分布變異，改進后的算法不僅能夠平衡局部和全局搜索，在收斂速度方面也優于其他4種算法。綜上所述，WSSA算法具有穩定性較強、收斂速度較快等特點。

4 結束語

本文針對基本SSA算法易陷入局部極值、后期種群多樣性減少等缺陷，提出了一種融合鯨魚優化算法和自適應分布變異的麻雀搜索算法（WSSA）。在SSA算法中，基于Tent混沌映射初始化種群，對發現者的位置融入鯨魚優化算法的泡泡網捕食機制進行更新，以平衡局部開發與全局搜索能力；加入自適應分布變異，增強算法跳出停滯的能力。但對于發現者、加入者、意識到危險麻雀的位置更新公式可做進一步改進。還可以將算法運用到實際問題中，如背包問題等，這也是接下來要解決的問題。