基于波箔片變形的浮動式箔片氣膜密封性能分析

徐潔，俞樹榮，丁雪興，蔣海濤，丁俊華

（蘭州理工大學石油化工學院，甘肅蘭州 730050）

引 言

航空發動機的設計一直是綜合強國優先發展的重大項目[1-2]，而先進的動密封技術是航空發動機研發的重要組成部分，也是影響航空發動機性能以及使用壽命的關鍵[3-4]。浮動式氣膜密封，通過鍥形間隙的動壓潤滑作用使轉子和浮環保持分離狀態，并利用帶壓氣膜實現非接觸密封[5]，因而在火箭渦輪泵、航空發動機系密封組件中得到了很好的應用[6-7]。但由于航空飛行器在運行過程中容易受到環境因素和自身結構帶來的隨機不確定性激勵[8-9]，機體俯仰角、偏航角、滾轉角的微小變化都可誘發失穩，從而導致浮環氣膜密封失效，影響整機工作[10]。

為提高運行的可靠性，國內外學者設計新型密封結構增強位移的包容性，其主流設計思路是用彈性結構代替或者支撐剛性密封端面。早在20 世紀90年代，NASA 基于箔片氣體徑向軸承的設計原理，針對航空發動機的應用，Salehi 等[11-12]提出了彈性箔片密封（compliant foil seal,CFS）結構，后期，美國宇航局格倫研究中心分別在發動機模擬工況條件[13]和室溫條件[14]下進行了密封試驗，表明其在高溫和大壓差下表現良好。Roberts 等[15]設計了具有柔性環形壁的密封件，這種柔性環形壁主要由單列獨立固定的彈性元件周向排列組成，它在保證足夠載荷的同時，允許燃氣渦輪發動機和排氣噴嘴之間的相對偏轉。Fang 等[16]在原有CFS 的設計基礎上，改變波箔片的方向，即拱波不再沿軸向布置，而是沿周向布置。此外，為了適應轉子偏移，也有學者沿用傳統剛性浮環，設計具有較大彈性的支撐系統來吸收徑向位移的振動能量。王虹等[17]將金屬橡膠彈性外環等效為阻尼器，提出一種新型氣膜密封阻尼結構(GFSD)，采用Newton-Raphson 法求解密封性能，并與直通式篦齒密封相比，結果表明壓力越大，GFSD表現越優異。Salehi 等[18]針對高速工況下的CFS 進行考慮湍流效應的密封性能計算，利用逐次超松弛求解流場和流體膜厚度的控制方程，發現壓差大于75 psi(1 psi=6.895 kPa)時，泊肅葉流占主導地位。馬綱等[19]設計了在密封支座連接柔性支撐的柱面密封，并利用有限元的數值方法求解瞬態雷諾方程，分析了密封系統穩定性與密封環質量之間的關系。張大鵬[20]分別進行了具有優化動壓槽的剛、柔性支承浮環密封試驗，并測試泄漏量，發現二者泄漏量變化趨勢基本保持一致，且柔性支承結構可有效減緩工況突變帶來的影響。近年來，昆明理工大學團隊關于柔性浮動式氣膜密封的探究較多，例如，康宇馳等[21]設計了分離式的浮動式箔片氣膜密封，且將波箔片沿圓周方向分段固定；Wang 等[22]分析了層流等溫下的T 型槽彈性箔片氣膜密封的靜、動態性能，表明了加長密封寬度可有效改善密封性能，但并未闡述箔片端面的相關參數和變形計算方式；同時，該團隊還將金屬鼓泡等作為柔性支撐結構[23-24]，并利用ANSYS軟件建立流固耦合數值模擬模型，分析了不同柔性支撐結構對浮動式氣膜密封流場以及密封環的影響。綜上所述，關于彈性箔片氣膜密封的研究主要集中在結構設計方面，除美國NASA 進行了部分理論和試驗測試外，國內學者也開展了柔性支撐密封的相關研究，但現有公開的彈性箔片氣膜密封的成果較少。

本文基于CFS 結構，根據彈性箔片氣膜密封的彈性端面結構和動壓槽型，同時考慮波箔片的剛度和阻尼，在柱坐標系下建立一端固定的波箔片和轉子進行同步圓運動時的氣膜厚度模型，并利用有限差分法與壓力雷諾方程聯立求解靜、動態密封性能參數。在平箔片表面的進口位置和中間位置分別開設直線動壓槽，考察兩種不同動壓槽位置對鍥形間隙內潤滑氣體厚度和動壓分布的作用情況，探尋壓力、轉速、摩擦因數和波箔片厚度對彈性箔片氣膜密封潤滑性能的影響規律。

1 浮動式箔片氣膜密封

1.1 結構分析

圖1 所示為浮動式箔片氣膜密封結構，主要是由密封腔、彈性波箔片、支承平箔片以及轉子系統組成。其中，轉子偏心安裝在腔體中，波箔片沿軸向分離且一端固定至密封腔體上，平箔片呈完整的環狀，并將高壓側的平箔片進行延伸，形成限制位移的延伸段，密封支座壓緊平箔片延伸段實現平箔片和波箔片的固定。借鑒剛性柱面氣膜密封動壓槽的設計，在平箔片表面開設性能較好的單列直線動壓槽[25]。

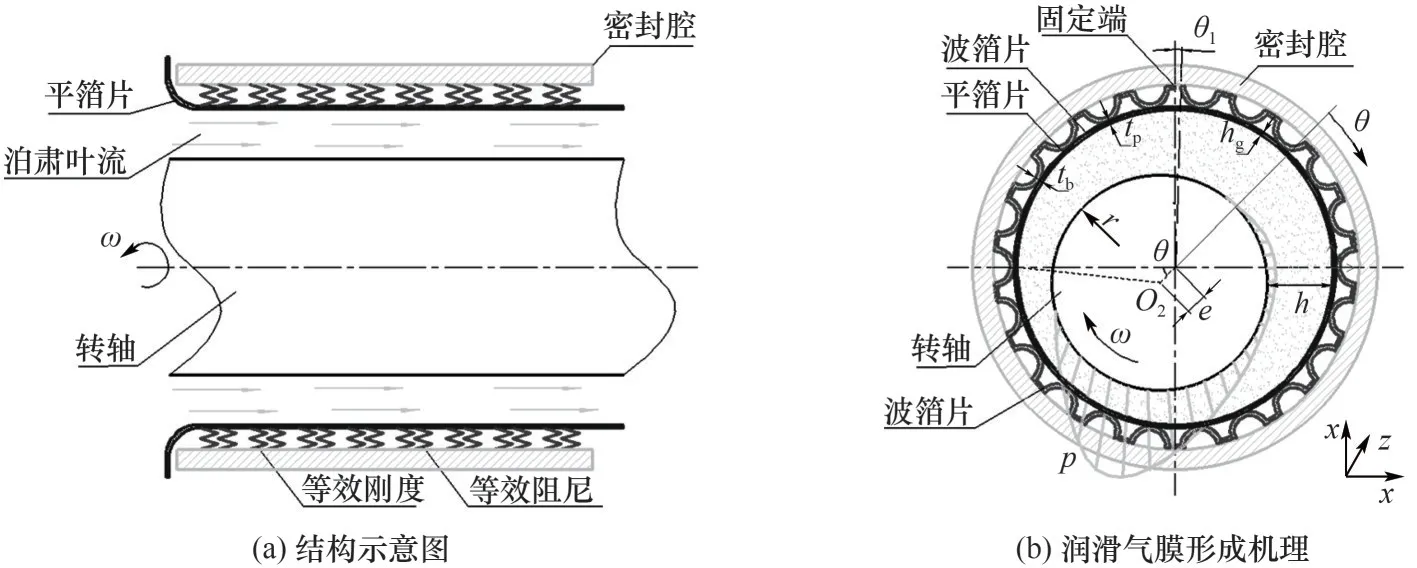
圖1 浮動式箔片氣膜密封Fig.1 Floating foil gas film seal

1.2 工作原理

波箔片頂部均與平箔片接觸，當在平箔片表面施加壓力載荷作用后，平箔片和波箔片會在受力方向發生變形，并從各自的固定端至自由端出現微小滑移[26]，如圖2 所示。當彈性箔片氣膜密封處于正常工作狀態時，氣體介質從高壓側流至低壓側，彈性箔片氣膜密封由于偏心距、動壓槽以及箔片變形的共同作用，在轉子與平箔片的微間隙內形成微米級環狀帶壓氣膜，保證了密封摩擦副始終處于分離狀態，以此實現潤滑和密封的效果[27]。

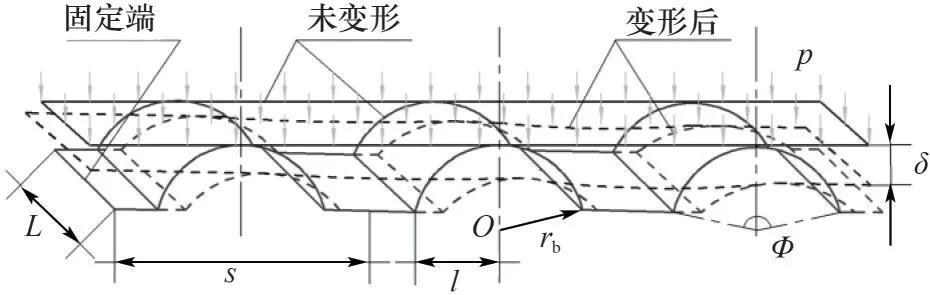
圖2 彈性箔片變形示意圖Fig.2 Schematic diagram of elastic foil deformation

2 理論模型的建立

2.1 箔片剛度模型

忽略平箔片在徑向方向的凹陷或凸起，僅考慮波箔片的變形。根據圖1，考慮波箔片與密封腔體的庫侖摩擦作用，利用Iordanoff[28]波箔片一端固定、一端自由的剛度模型表征波箔片的變形，如式(1)所示。

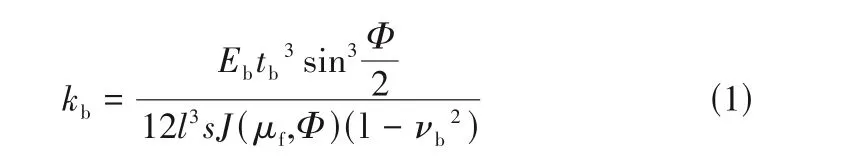
式中，J為與波箔片角度Φ與摩擦因數μf有關的函數，如式(2)和式(3)所示。

2.2 密封特性求解模型

假設流場為層流，流固界面間無滑移，密封介質為理想氣體，物性參數保持不變，可得流體動壓潤滑模型：

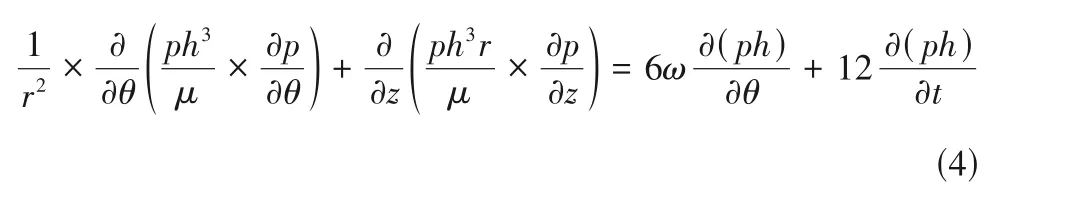
式中，p為計算得到的靜態氣膜壓力，Pa；t為運動時間，s。渦動頻率比為1。

相較于傳統浮動式氣膜密封，彈性箔片密封的氣膜厚度還需考慮箔片變形的影響，因而，靜態時槽區和非槽區的氣膜厚度可通過式(5)計算。

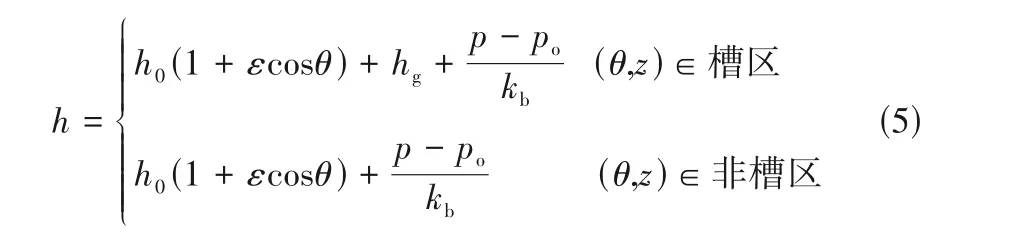
當受到(Δx,Δy)的位移擾動和(Δx˙,Δy˙)的速度擾動后，得到包含擾動參數的氣膜壓力、氣膜厚度以及箔片變形量的Taylor級數展開式

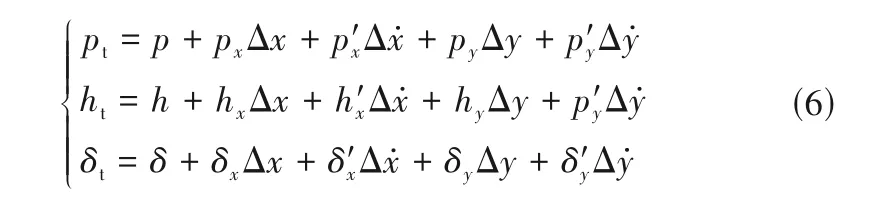
考慮時間項后，氣膜厚度偏離靜態氣膜厚度h，得到微擾下的氣膜厚度

式中，Δh= Δxsinφ- Δycosφ；δt為由擾動引起的波箔片變形量，μm。聯立式(6)、式(7)可得

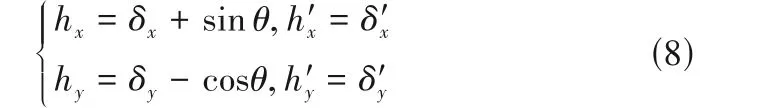
擾動條件下波箔片的力平衡方程為

式中，[kb]，[cb]分別為波箔片的剛度矩陣和阻尼矩陣，cb= 5.00 × 106Pa · s/m；{F}為氣膜壓力矢量。

將式(6)、式(8)代入式(9)，可得：

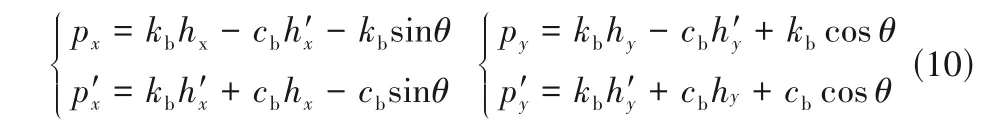
2.3 密封性能參數

評價浮動式箔片氣膜密封的關鍵靜態特性參數有氣膜浮升力和質量泄漏率，動態特性參數有主剛度和主阻尼系數，以下為各表達式。

氣膜浮升力

式中，Fh，Fv分別為氣膜浮升力的水平方向和豎直方向的分量。

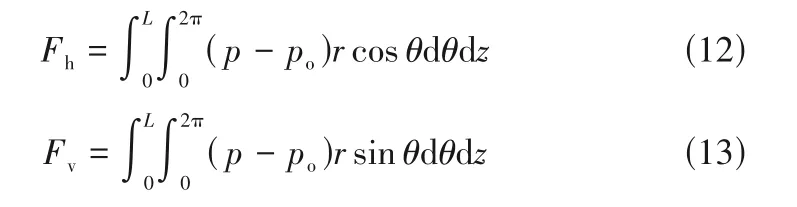
質量泄漏率

氣膜主剛度系數

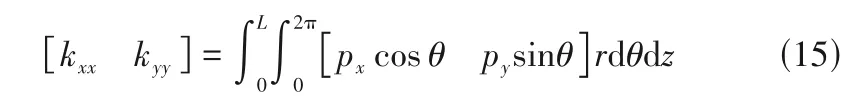
氣膜主阻尼系數

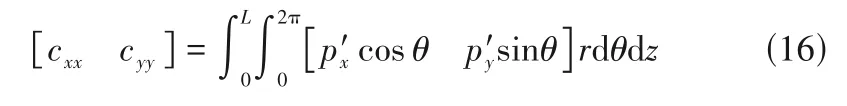
2.4 邊界條件

在進出口有強制性邊界

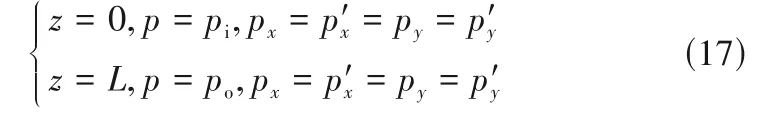
在中截面有循環邊界

2.5 網格劃分與迭代計算

沿周向和軸向劃分網格數，如圖3所示。

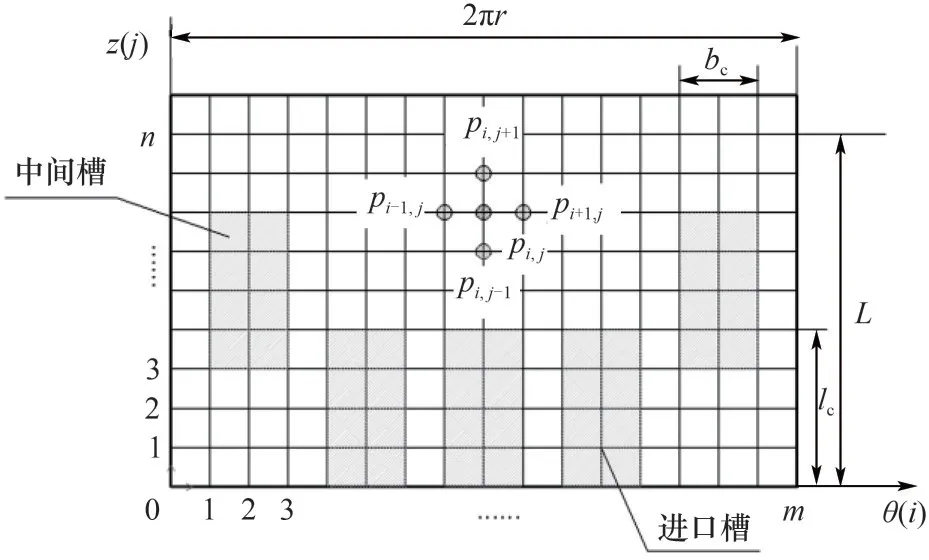
圖3 計算域網格劃分Fig.3 Computational domain meshing

利用有限差分法對靜、動態求解方程進行離散，并在迭代計算時采用超松弛迭代：

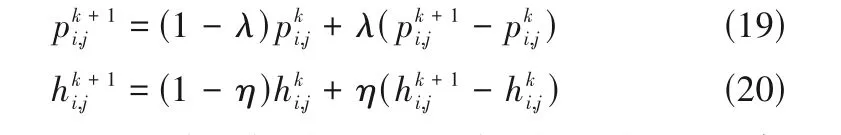
式中，λ，η分別為氣膜壓力和氣膜厚度的迭代因子；k為迭代次數。浮動式箔片氣膜密封的特性參數計算流程如圖4所示，圖中err= 1 × 10-6。

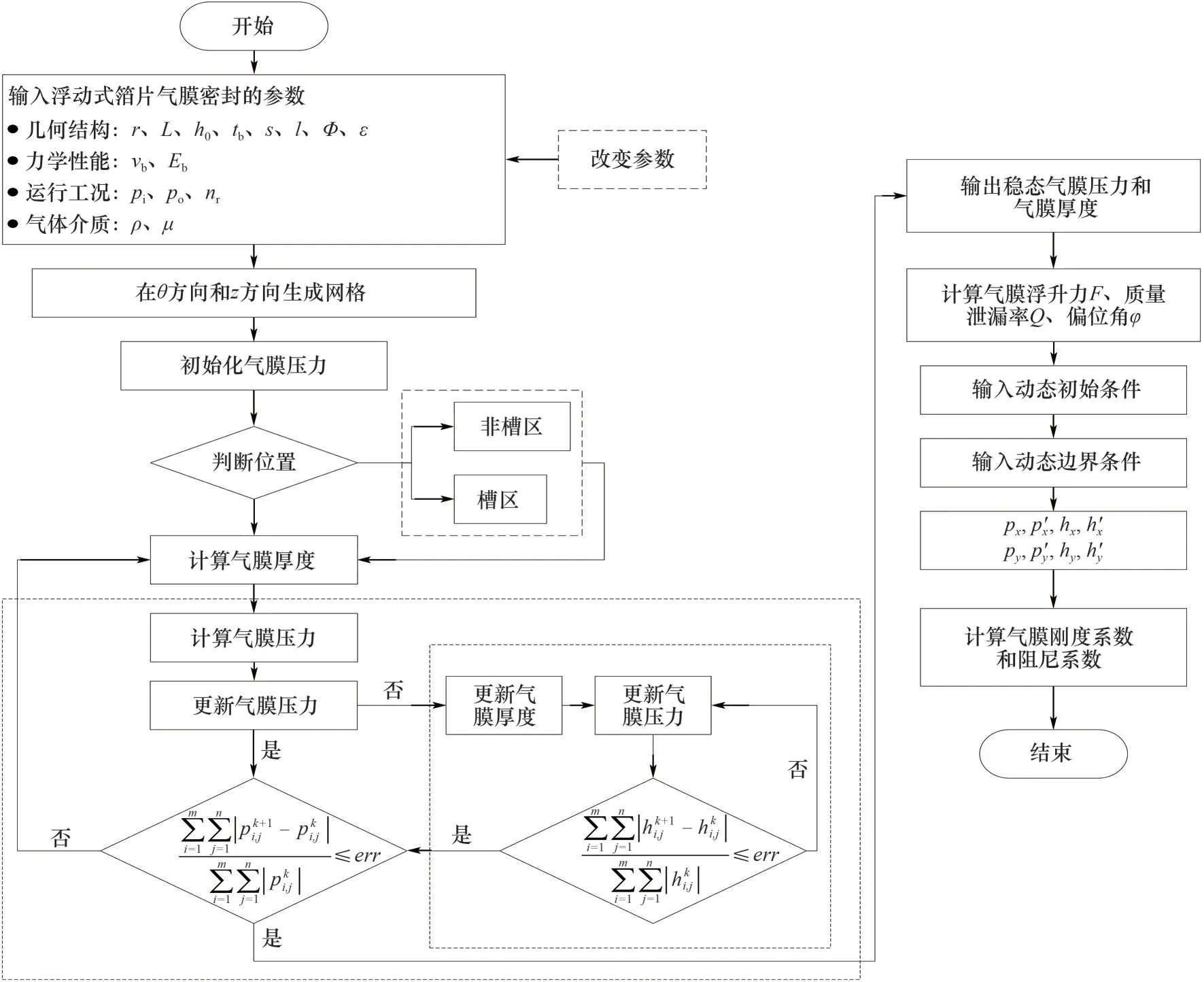
圖4 計算流程圖Fig.4 Calculation flow chart

3 參數選取與討論

3.1 結構參數與力學性能

浮動式箔片氣膜密封的結構參數和力學性能如表1所示。

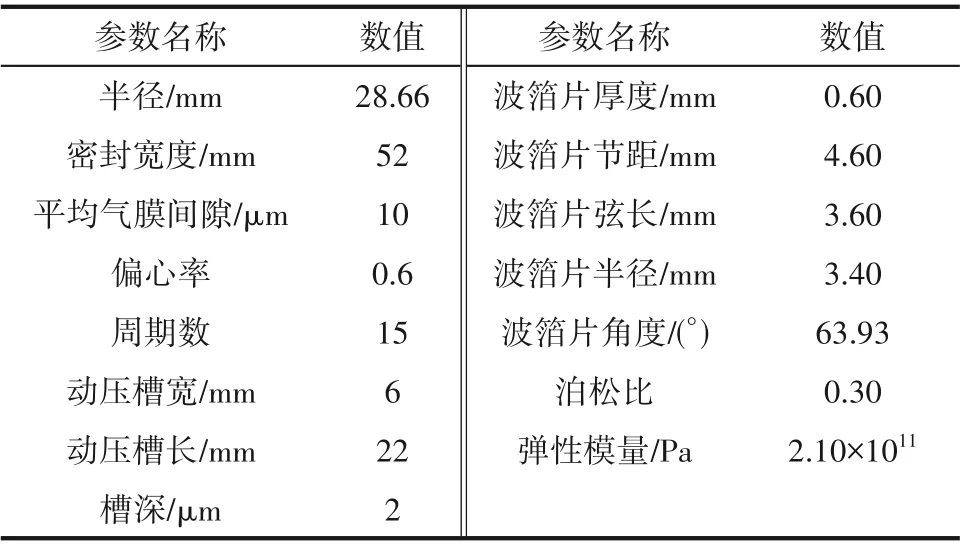
表1 結構參數與力學性能Table 1 Structural parameters and mechanical properties

3.2 工況參數

表2 為浮動式箔片氣膜密封的工況參數(介質為空氣)。

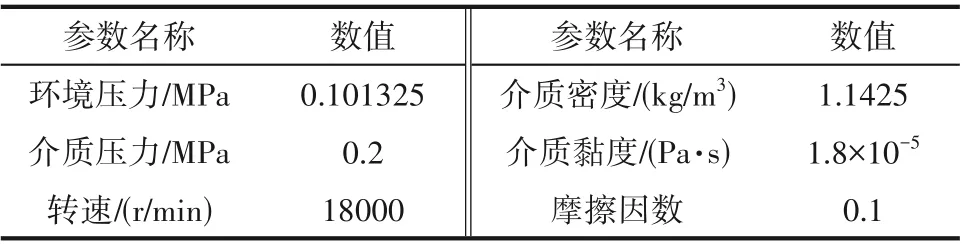
表2 工況參數Table 2 Working condition parameters

3.3 程序正確性驗證

3.3.1 流場計算程序驗證 為驗證流場計算的正確性，選擇文獻[29]中無槽剛性浮環的結構參數進行流場計算程序的正確性驗證，對比結果如圖5 所示。當偏心率為0.5 時，有最大相對誤差(P)為5.76%，表明本文流場計算程序具有一定可靠性。

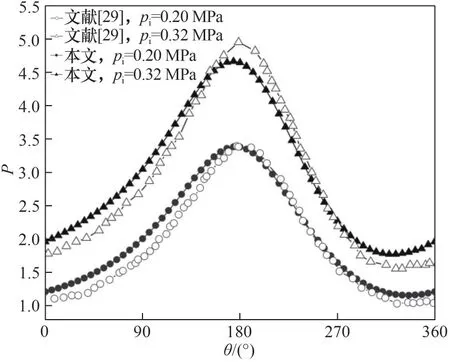
圖5 流場計算程序驗證Fig.5 Verification of flow field calculation program

3.3.2 剛度計算程序驗證 選擇文獻[30]中的波箔片結構參數，驗證波箔片剛度模型和計算程序的正確性，對比結果如表3 所示，同時，閆佳佳[30]針對徑向箔片軸承進行研究時利用該剛度模型進行計算，并與NASA 試驗數據[31]對比驗證了準確性，說明該剛度模型具有一定的可用性。

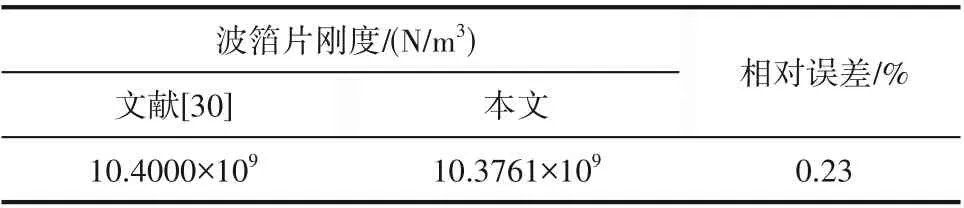
表3 剛度計算程序正確性驗證Table 3 Verification of the correctness of the stiffness calculation program

4 計算結果與分析

以表1、表2 的工況參數和結構參數進行計算，獲得進口直線槽和中間直線槽的波箔片變形分布如圖6 所示，氣膜厚度分布如圖7 所示，氣膜壓力分布如圖8所示。

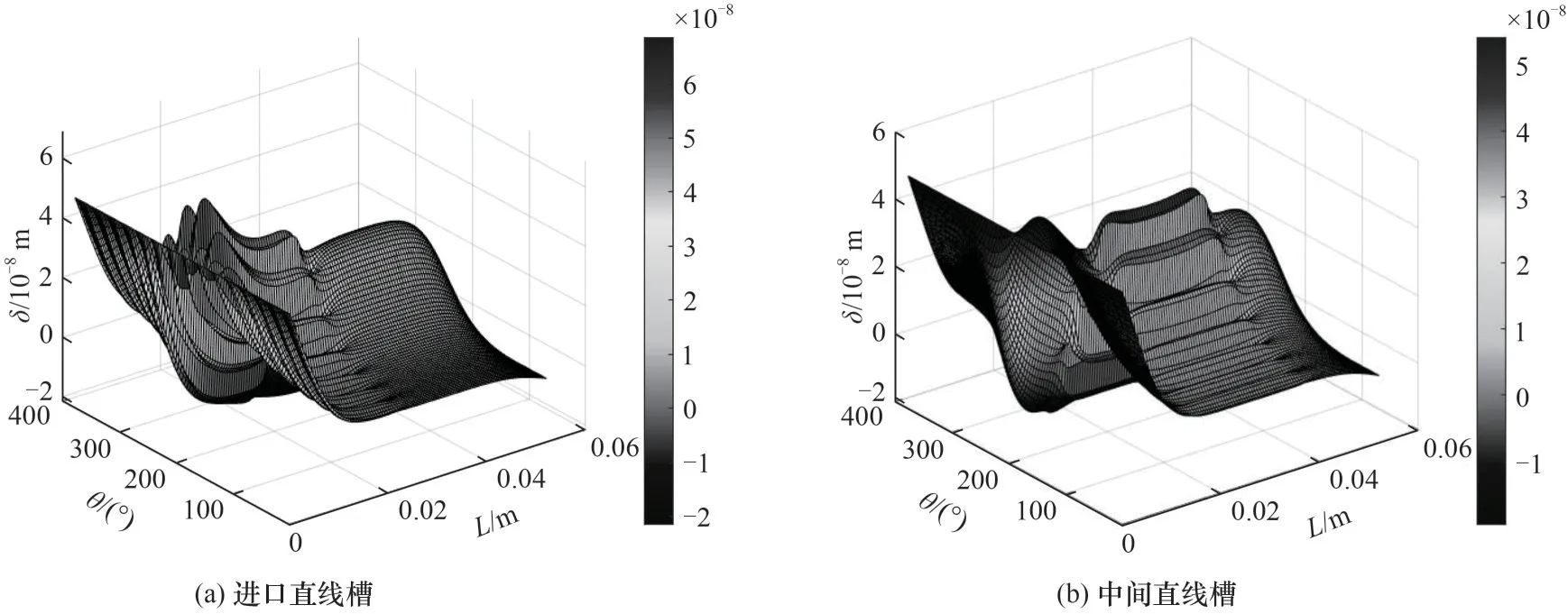
圖6 波箔片變形分布Fig.6 Distribution of bump foil deformation

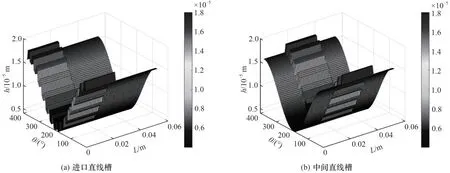
圖7 氣膜厚度分布Fig.7 Distribution of gas film pressure

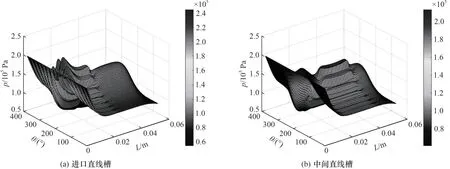
圖8 氣膜壓力分布Fig.8 Distribution of gas film pressure

由于直線槽分布位置的不同，所表現出來的流場特性也有所不同。對比圖6、圖7 可以發現，在氣膜厚度分布的最小區域，存在最大的波箔片變形量，但氣膜厚度沿著圓周方向呈余弦狀，整體分布表現出更強的對稱性，由于動壓槽的存在，氣膜厚度在微尺度臺階處出現不連續性。兩種直線槽最小氣膜厚度均位于壓力出口處，進口直線槽的最大和最小氣膜厚度分別為18.02 和4.00 μm，中間直線槽的最大和最小氣膜厚度分別為17.97和4.00 μm。

根據圖8 氣膜壓力分布所示，在θ=180°位置的高壓側附近，出現最大氣膜壓力，壓力在動壓槽區域呈現一定幅度的波動，隨著圓周角度向對稱邊界變化，氣膜厚度逐漸增大，氣膜壓力逐漸減小，壓力波動幅值逐漸減小。對比圖8(a)、(b)，在動壓效應和鍥形效應的共同作用下，氣體流動至進口直線槽后，氣膜壓力略微上升，在壓力進口附近有氣膜壓力最大值(0.24 MPa)，之后緩慢減小，當氣體流經動壓槽根部之后，由于節流效應氣膜壓力明顯下降，直至在密封端面的末端部分達到環境壓力。對于分布有中間直線槽的流場，最大氣膜壓力為0.21 MPa，氣膜壓力從進口處就開始緩慢減小，當氣體流入中間直線槽后氣膜壓力小幅度增大，隨后緩慢減小。同時可以發現，流體域內的氣膜壓力并不是完全大于環境壓力，而是在氣膜壓力較高區域附近出現了負壓，這是由于偏心作用和壓差作用導致的，吸附效應使得波箔片發生變形，氣膜厚度也在負壓分布區域減小。

4.1 進口壓力的影響

圖9(a)給出了不同直線槽分布位置下氣膜浮升力、質量泄漏率與進口壓力的關系曲線。當進口壓力在0.12～0.26 MPa范圍內變化時，進口直線槽的氣膜浮升力和質量泄漏率始終大于中間直線槽。隨著進口壓力上升，氣膜浮升力也呈單調性上升趨勢，進口直線槽的氣膜浮升力增加了8.86%，中間直線槽的氣膜浮升力增加了8.32%，可見，進口壓力變化引起的氣膜浮升力變化幅度較小，這是由于進口壓力越大，波箔片背離軸心方向的變形越大，從而氣膜厚度越大，這在一定程度上削弱了進口壓力帶來的整體流域內壓力的增大效應。進口壓力增大加速了徑向的泊肅葉流動，較多的氣體介質從高壓側流至低壓側，同時，密封面的變形也導致泄漏通道增大，因而進口壓力對質量泄漏率的影響顯著，進口直線槽的泄漏率從1.48×10-4kg/s 增加至2.16×10-3kg/s，中間直線槽的泄漏率從1.30×10-4kg/s增加至1.72×10-3kg/s，當進口壓力較小時，兩種動壓槽位置的泄漏率計算結果差值較小，相較于分布在中間位置的直線槽，高壓側附近的進口直線槽更容易受到進口壓力的影響，泄漏率增幅更大。

圖9(b)給出了動態特性參數與進口壓力的關系曲線，進口直線槽和中間直線槽的主剛度kxx為正、主剛度kyy為負，且二者具有相似的變化規律，低壓工況下兩種動壓槽位置的主剛度kxx差別很小，之后均隨進口壓力的升高而緩慢降低，其中進口直線槽的下降速率更快，這說明進口壓力增大氣膜厚度迅速增大，當進口壓力為0.26 MPa 時，進口直線槽有最小剛度系數4.66×106N/m，中間直線槽有最小剛度系數4.47×106N/m。進口直線槽和中間直線槽的主阻尼cxx與主阻尼cyy變化趨勢呈對稱狀態，且均逐漸趨于零。

圖9 進口壓力的影響Fig.9 Influence of inlet pressure

4.2 轉速的影響

由圖10(a)可以看出，當轉速從8000 r/min 增大至22000 r/min 時，氣膜浮升力顯著提高，且基本呈線性增大趨勢，進口直線槽的氣膜浮升力增加了2.99 倍，中間直線槽的氣膜浮升力增加了3.09 倍。由于加速的庫埃特流動對軸向方向的流動影響很小，因而質量泄漏率基本不隨轉速的增大發生改變。其中，進口直線槽的質量泄漏率維持在1.11×10-3kg/s，中間直線槽的質量泄漏率維持在0.89×10-4kg/s。轉速增大，氣體動壓效應增強，最大氣膜壓力迅速增大，階梯效應增強，高壓附近區域的最小氣膜壓力也隨之減小，但承壓區域比負壓區域的面積增率大[32-33]，因而浮動式箔片氣膜密封的浮升力隨轉速的增大而增大。轉速增大引起的這種流場現象也導致浮動式箔片密封的氣膜主剛度kxx和kyy的絕對值均隨著轉速的增大而增大。由圖10(b)可以看出，主阻尼cxx和cyy均隨著轉速的升高從負值上升為正值，呈現出拋物線式的上升趨勢，并逐漸趨于平穩，說明浮動式箔片密封適應高轉速的工況條件。

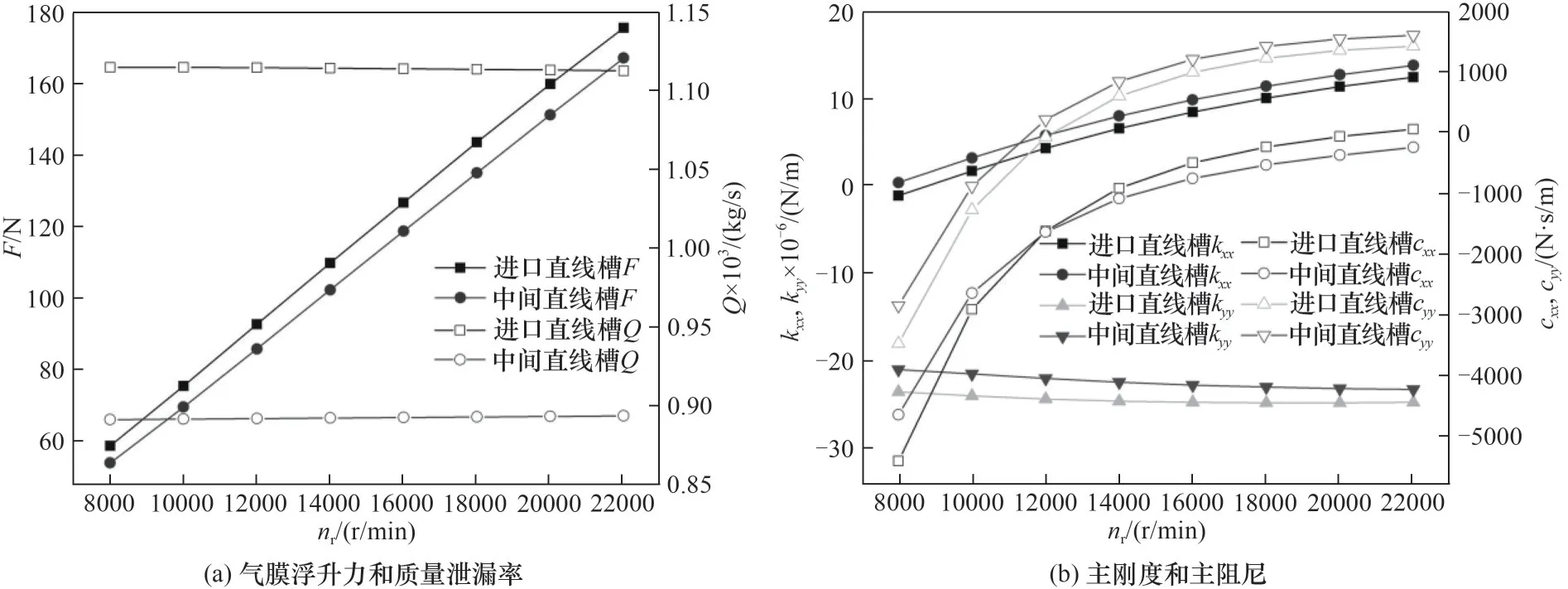
圖10 轉速的影響Fig.10 Influence of speed

4.3 摩擦因數的影響

圖11(a)給出了庫侖摩擦因數與浮動式箔片氣膜密封靜態密封特性的關系，隨著摩擦因數的不斷增加，進口直線槽和中間直線槽的質量泄漏率均呈現出略微下降的趨勢，減小量可以忽略不計。在實際運行過程中，由于波箔片發生滑移，必定與發生接觸的密封腔間存在庫侖摩擦，這在一定程度上增大了波箔片的剛度，箔片變形量減小，最大氣膜厚度和最小氣膜厚度均減小，鍥形效應加強，因而氣膜浮升力增大。當摩擦因數從0 增大至0.28 時，進口直線槽和中間直線槽的浮升力分別增大了1.74 和1.40 N，說明摩擦因數變化對氣膜浮升力的影響很小。

圖11(b)給出了庫侖摩擦因數與浮動式箔片氣膜密封動態密封特性的關系，摩擦因數增大，兩種直線動壓槽對應的氣膜主剛度kxx和kyy都輕微提高，并保持相對穩定的差值，中間直線槽的主剛度均大于進口直線槽，主阻尼反而均小于進口直線槽，究其原因，摩擦因數增大，氣膜厚度增大量較小，使得氣膜阻尼效果變弱。

圖11 摩擦因數的影響Fig.11 Influence of friction factor

4.4 波箔片厚度的影響

圖12(a)為波箔片厚度在0.20～0.90 mm 范圍內變化時對各關鍵參數的影響規律，從圖中可以看出，波箔片厚度增大，增強了結構自身在徑向方向的支撐能力，使得彈性端面不易在受力方向產生位移，加強了鍥形效應，因此氣膜浮升力提升，質量泄漏率減小，當波箔片為0.90 mm 時，進口直線槽有最大氣膜浮升力127.99 N 和最小質量泄漏量1.11×10-3kg/s，中間直線槽有最大氣膜浮升力119.93 N和最小質量泄漏量0.89×10-3kg/s，但這種加壓和控漏作用不是無限加強的，而是逐漸變緩的，說明當波箔片厚度趨于某一較大值時對端面剛度的影響減弱，甚至不發生影響，密封端面接近剛性化。

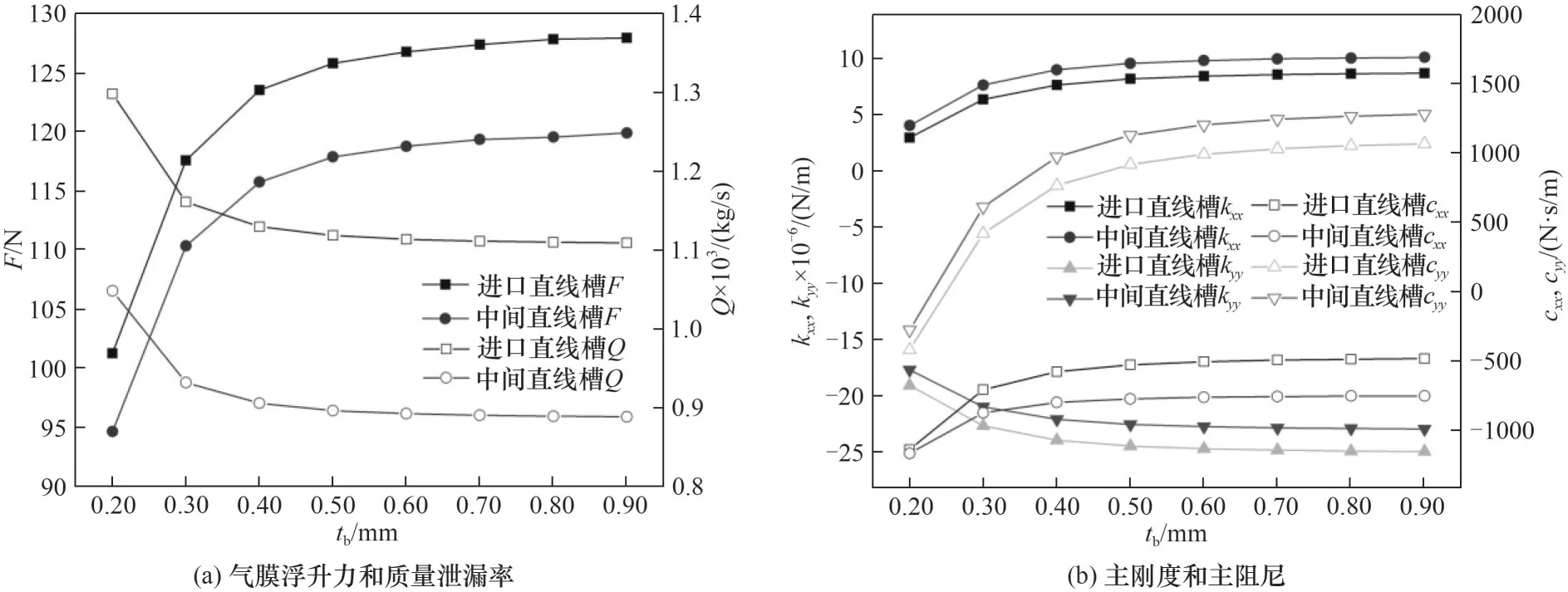
圖12 波箔片厚度的影響Fig.12 Influence of bump foil thickness

從圖12(b)可以看出，氣膜主剛度kxx、主阻尼cxx和cyy均隨著波箔片厚度的增大而增大，密封端面不易變形，密封間隙增量減小，導致氣膜的承載力上升，所以氣膜主剛度的絕對值大小將會有所上升。對于進口直線槽，0.90 mm 波箔片厚度的主剛度kxx均為0.20 mm 的2.89 倍，主剛度kyy均為0.20 mm 的1.01 倍；對于中間直線槽，0.90 mm 波箔片厚度的主剛度kxx均為0.20 mm 的2.49 倍，主剛度kyy均為0.20 mm 的1.30 倍，這是由于浮動式箔片氣膜密封承擔的主要載荷作用在x方向上，因此主剛度kxx的增幅略大于主剛度kyy。

5 結 論

本文研究主要得到以下結論。

(1)浮動式箔片氣膜密封的密封特性與流場分布和密封端面的變形相關，在最小氣膜厚度處，氣膜壓力最大，對應的波箔片變形最大。

(2)進口直線槽的氣膜浮升力和質量泄漏率均大于中間直線槽，進口直線槽對進口壓力的變化更敏感。

(3)在浮動式箔片氣膜密封中，庫侖摩擦效應使密封副表面變“剛”，但相比于庫侖摩擦效應的影響，波箔片厚度增大，剛度的增大效果更加明顯，對密封性能的影響也更大。

(4)氣膜浮升力和質量泄漏率均隨著進口壓力增大而增大，但氣膜主剛度反而減小；氣膜浮升力、氣膜主剛度kxx以及主阻尼均隨著轉速的增大而增大，而主阻尼逐漸趨于穩定，轉速變化對質量泄漏率基本不發生影響。

(5)較大的摩擦因數和波箔片厚度，密封端面的變形量減小，氣膜厚度增量減小，動壓效應增強，氣膜浮升力、主剛度以及主阻尼在小范圍內增大。

(6)為滿足高速高溫環境下航空發動機的軸端動密封設計，還需考慮平箔片的彎曲變形，并結合試驗完善修正，從而建立更精確的浮動式箔片氣膜密封數值計算模型。

符 號 說 明

bc——槽寬，mm

cb——阻尼系數，Pa·s/m

cxx，cyy——氣膜阻尼，N·s/m

Eb——波箔片彈性模量，GPa

e——偏心距

F——氣膜浮升力，N

{F}——氣膜壓力矢量

Ff——摩擦力，N

h——氣膜厚度，μm

hg——動壓槽槽深，μm

h0——平均氣膜厚度，μm

k——迭代次數

kb——波箔片剛度，N/m3

kxx，kyy——氣膜剛度，N/m

L——密封寬度，mm

l——波箔片弦長的一半，mm

lc——槽長，mm

nr——轉速，r/min

p——氣膜任意一點壓力，MPa

pi——進口壓力，MPa

po——出口壓力，MPa

Q——質量泄漏率，kg/s

r——旋轉軸半徑，mm

rb——波箔片半徑，mm

s——波箔片節距，mm

t——運動時間，s

tb——波箔片厚度，mm

tp——平箔片厚度，mm

vb——波箔片泊松比

z——軸向坐標

δ——箔片變形量，μm

ε——偏心率

η——氣膜厚度迭代因子

θ——周向角度，(°)

θ1——波箔片自由端與固定端形成的角度，(°)

λ——氣膜壓力迭代因子

μ——介質黏度，Pa·s

μf——波箔片與密封腔的摩擦因數

ρ——介質密度，kg/m3

Φ——波箔片角度，(°)

φ——偏位角，(°)

ω——轉速，rad/s

下角標

h——水平方向

t——動態相關參數

v——豎直方向

x——x方向微擾分量

y——y方向微擾分量