QMC方法在數量金融中的新挑戰分析

趙倩

摘要：在新時期環境下，我國金融領域的發展十分迅速，而在金融領域的發展中產生了多樣化的金融產品，而在金融工作開展中往往面臨諸多的金融問題，為了實現對此類問題的解決，金融模型的應用十分重要，但因為金融模型存在復雜性，對很多的金融問題都不能有效解決，而QMC作為一種廣泛使用的方法也在數量金融中存在著諸多挑戰。文章就主要針對QMC方法在數量金融中的新挑戰進行分析，希望對相關工作的研究提供參考。

關鍵詞：QMC方法;金融領域;數量金融;金融問題

在如今金融市場中，具有復雜性的特點，為了促進其能夠有效發展，需要使用到大量個性化的金融工具，而金融模型則是對金融情況刻畫的重要手段。由于金融模型在建立中呈現出顯著復雜性特點，且易受到諸多因素的影響，使大量金融方面的問題并不可以得到顯式的求解，而QMC方法就是一種對復雜性金融問題解決的數值方法，但此方法在使用中還存在諸多的難題需要克服，而這就是本文主要研究的內容。

一、QMC方法概述

通過傳統數值的積分法并不能夠對高維積分問題解決，且要被積的函數還需要在光滑性方面符合要求，如梯形法使用中要求其被積函數的二階導數要在連續性方面呈現一定條件，而辛普森的法則要求其被積函數的四階導數要具有良好連續性。對于很多金融的問題來說，其目標函數在光滑性方面一般都不滿足條件，且維數也往往很高，所以在對傳統數值的積分法使用中，不能保證使用的效果，但MC方法則能夠實現對此類困難的克服。此MC方法公式為：

在上式中，只要相應的積分存在，可通過強大數的定律獲取：

這說明I^n（f）為I（f）強結合的估計，且說明MC的方法具有十分廣泛適用范圍，進一步若存在I（f2），則I^n（f）估計量均方根的誤差是：

在上式內，σ2=I（f2）-I（f）2，表明了此MC 方法于概率意義誤差中具有O（n-1/2）收斂階，并不對維數d產生依賴。若d>4的話，此MC方法具有收斂的速度比梯形法則收斂速度要快。若d>8，此MC方法的收斂速度比辛普森的法則收斂速度要快。盡管MC方法可以對維數的災難等相關問題實現有效克服，但同樣其還存在一定的缺陷需要解決，主要體現在它只存在概率意義中誤差界，和傳統數值積分存在確定誤差界不一樣;它對全部類型被積的函數，不管此函數是不是光滑，此MC方法具有一樣的收斂階，當面對一些呈現出更加光滑特性的函數，使用此MC方法不能得到更高收斂階，若使用傳統數值的積分就能夠滿足要求;計算機對理想化隨機點列很難生成，往往只能對偽隨機的點列生成。

二、高維和間斷對QMC方法產生的影響

（一）高維對QMC方法產生的影響

大量金融問題的維數都會超過上千的情況，比較常見的有期權定價的問題等，基于QMC法O（n-1（log n）d）收斂階分析，此QMC法是不利于對高維問題解決的，這主要是即使對較為適中性維數來說，此QMC法其收斂階中（log n）d對數項亦可能十分大。如d=8時，想要達到n-1（log n）d<n-1/2的情況，要求n不低于1029×1.79，而實際中此數量級樣本量很難得到實現。但通過眾多的實證研究得知，即使金融問題達到數百維，此QMC的方法還是比MC的方法要優越得多，面對此種情況，很多學者也進行了合理解釋。

一些學者闡述了在對一些加權的函數類中，以QMC法對其維數災難的相關問題實現有效解決;還存在一種解釋則是基于有效維數概念的。一些學者發現在諸多高維的金融問題中存在較低有效的維數，在加入函數 f后可以對其寫成兩部分的內容，也就是 fL和 fH，且fL與fH呈現出正交的關系，且fH具有的方差其實只占到f方差極小的比例，fL維數是有效的維數。因為一維投影是低偏差的序列，和前幾維的投影比其隨機序列具有更好均勻性，但其后幾維的投影存在均勻性的不理想，所以當存在較小的有效維數時，此QMC的方法能夠對fL很好處理，也許它并不能夠對 fH很好處理，但此函數并不會對整體的誤差存在較大貢獻，這也就說明了 QMC的方法為什么能夠對低有效的維數金融問題成功處理。

因為QMC的方法效率遭受維數影響，大量研究嘗試借助減小有效的維數對QMC效率提升。尤其對金融的問題，通過合適路徑模擬法能夠對問題有效維數減小。在一些研究中，表明了一些路徑的模擬法比標準路徑的模擬法存在更好表現效果，如布朗橋方法和主成分的分析方法等，但它們都存在相同缺陷，其并非對目標的函數特征實施充分考慮，則它們的效率還是對問題實際特性產生依賴。

（二）間斷對QMC方法產生的影響分析

上文所提路徑的模擬方法，只是出于對有效維數減小的目的，同時目標函數具有的光滑性同樣對QMC的方法效率產生制約。在一些研究中，面對不連續的函數提出一種OT法（正交變換法），這也表明路徑模擬法實現對間斷性的特征顯著的影響，且還通過對一類路徑的模擬法設計，讓間斷的結構產生對QMC法的“友好性”。

面對諸多的金融問題，如期權定價以及Greeks計算等，涉及一個或多個數量不光滑結構，對他們主要進行兩種常見類型的歸納，一種是間斷結構，表示為I{ψ≥0}，還有一種是折褶結構，表示為max（ψ（x），0），且ψ（x）代表Rd中連續性的函數，此研究表明了目標函數具有不光滑性對QMC法效率產生了影響。一些研究中提出QMC法的性能發生退化現象，主要是因為被積的函數自身呈現間斷點或者在光滑性方面存在不足而造成的;還在一些研究中觀察出，折褶的結構通過ANOVA的分解會呈現出光滑的低階項情況，且其光滑性會對路徑模擬法的使用較為依賴。對金融的應用方面，一些研究使用路徑模擬法對間斷結構改變，從而獲取QMC的友好型間斷點;一些研究中對相關數值分析結果表明，對變換后間斷結構來說，此QMC法效率得到了顯著的提升，但在研究中還普遍存在方法局限性的問題，往往只對單個間斷的結構目標函數實施考慮，并未結合多個間斷的結構以及多個的折褶結構，實現全面考慮與綜合分析，而這也意味著對具多個數量非光滑的結構奇異期權，此OT方法就得不到有效使用。面對此類缺陷，就需要針對多個數量非光滑的結構設計出一種路徑模擬的方法，即QR法。此QR法能夠按照非光滑的結構重要性實施變換，讓比較重要非光滑的結構對更少變量依賴，提供一種度量、非光滑習慣結構的重要性指標，基于此，可以對此類非光滑的結構重要性實施排序，后變換處理，通過數值結果分析此方式對非光滑的結構變換，能夠對QMC的方法效率實現顯著提升。

三、QMC方法在數量金融中的降維和間斷處理

（一）QMC方法在數量金融中的降維處理

對布朗運動初始生成的矩陣Ao給定，把收益函數進行獨立性標準的正態變量寫成，表示為z=（z1，...，zd）T～ N（0，Id）的G（z）函數，并用H（A0z）代表。面對任意的正交陣U情況，通過E[G（z）]=B[G（Uz）]能夠得知，被積函數對G（z）或者G（Uz）選擇具有等價性。對連續光滑性G（z）目標函數考慮，如何找到一個正交的矩陣U讓QMC法來對G（Uz）函數的效率實現盡可能提升，是需要重點研究的內容。

如果G（z）被積函數是一線性的函數，則LT方法不斷在任意點展開均能夠對函數線性的結構抓住，所選擇正交陣ULT能夠把截斷的維數降到1維。但是如果G（z）被積函數是一較為復雜性、非線性的函數，則LT方法于若干個數量給定點展開信息的話，可能并不會對被積函數重要結構很好解釋。而對G（z）復雜性被積函數，一些學者提出了一個匹配的策略，也就是對G（z）函數選擇某點Taylor的展開式當作G（z）原函數匹配的函數。具體來說，此函數表示為G1（z）=G（zo）+▽G（zo）T（z-z0），zo∈Rd，此函數可當作G（z）函數的匹配性函數。一些學生提出了QR方法，能夠直接用在較簡單函數G（z），且求得出一個正交的方陣U，讓使G1{Uz}截斷的維數得到顯著降低，把正交的方陣U用在原函數的G（z）中，其效果主要對匹配的函數G（z）和原函數的G（z）中接近程度較為依賴。

（二）QMC方法在數量金融中的間斷處理

在對非光滑的結構重要性實施排序和變換后，盡管按照此方式實現非光滑的結構變換，能夠有效促進QMC的方法效率提升，但其間斷點依然存在。這就說明完成變換的間斷性結構還可能對QMC的方法效率產生一定的影響，因此另一種對QMC的方法效率提升的策略是對目標的函數間斷點移除。現階段，諸多光滑化的方法在MC的方法或其他領域中普遍使用。在通過pathwise法對敏感性的參數估算時，其收益函數間斷點往往會使此方法發生失效，為了對pathwise法使用，可以通過條件的期望來對此類間斷點移除，從而獲取一個光滑性無偏的估計;一些研究提出通過對敏感性的參數計算來實現核估計，其能夠對含間斷點收益函數進行處理，但此核光滑的技術所獲取有偏的估計，且實際操作中很難對其估計的誤差把握;面對障礙期權的定價問題情況，一些研究在障礙的條件下來對標的的資產演變過程實施條件的抽樣，獲取一個光滑無偏的估計;一些人員針對亞式的期權提出一種條件的MC法，此種方法以收益函數為基礎關于股票的價格幾何性平均值條件具有的期望存在閉合的解。關于光滑技術以及路徑模擬的方法結合的QMC法是很少的，一些研究根據障礙期權進行一種結合了LT法條件抽樣的模式引入，且還把此方法向Heston的模型推廣。

通過對諸多方法綜合分析，提出一種VPO的光滑化法，并和此光滑化法以及一些路徑的模擬法結合，來對帶有間斷的結構金融問題進行解決。此方法和條件MC的方法存在不同，在本文中所提出VPO的光滑化法不需事先對條件期望計算，但其VPO的光滑化法要求此被積函數間斷的結構符合相應條件。對存在的一些金融方面問題，通過設計出合適路徑模擬的方法對此類條件滿足，但并非全部路徑模擬的方法都符合VPO的光滑化法所需條件。為了使此光滑化的方法對常見金融問題適用，就要對QR法實施修正，稱作MQR法，此MQR法可以如QR法一樣按照間斷結構重要性實施處理，且它能夠和VPO的光滑化法結合，此兩種方法結合可以對間斷點消除，且還能夠對有效維數雙重效果減小。

四、QMC方法在數量金融中的應用分析

（一）普通QMC方法在多期收入的保證價格應用

在多期收入C（0）保證價格中，“多期”主要在數學方面體現出路徑的依賴，也就是要求模擬成η（t）整個的路徑，此時要對w（t）和N（t）增量的獨立性考慮，將T[0，T]時間區間等分作J份，其步長為dt=T/J，表示為0<dt<…<Jdt=T，dW（j）=w（t）-（t-dt）-N（0，dt），生成出dw（j）估計為：dw（j）=，且Z-N（0，1），同理可得dw（j）=、dN（j）=N（t）-N（t-dt）～P（λdt），其中dN（k）=P。在dN（k）的生成中，Pλdt-P（λt）在生成出dW（j）與dN（k）之后，會再生成出InK（1）-N（μ，σ2），后將三個數量隨機向相關公式帶入，得到C（0）公式內顯著性水平α置信的區間。

（二）條件QMC方法在多期收入的保證價格應用

對X目標函數的表達式表示為Xi=（η·（t）-γ）+，進而進一步對E（Xt|Wt），歐式的看漲期權馬爾可夫的性質在任意的時刻價格是：

結合標的Sto（t）其服從幾何的布朗運動，最終能夠得到顯著性的水平α置信的區間。

（三）應用結果分析

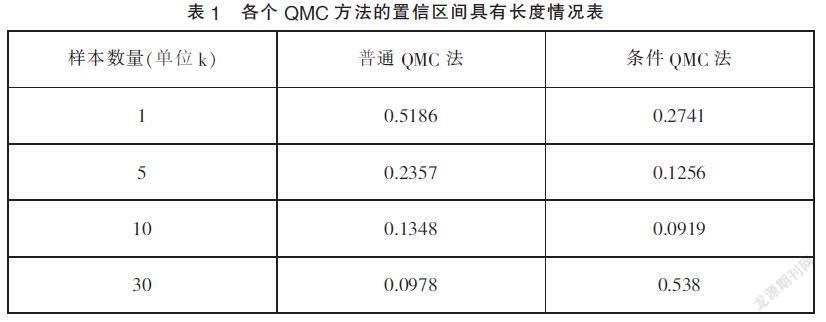
所給定的參數值置信區間的長度幾乎不存在區別，但在動態化參數值下，期置信的區間長度情況如表1。

從表1分析可得，普通QMC法具有模擬的精確度是最差的，對偶的變量法及控制的變量法具有相似的精確度，且控制的變量法要略好一點，條件QMC法具有最高的精確度。而之所以出現這樣的情況，是因為條件QMC法對條件期望解析解進行使用，數值的解精度即使再高也不可能比解析解更高。但即使有解析解的存在，此條件期望的解析解存在此前提條件也是很難實現的。因此能夠看出，得到條件期望解析公式其實并非易事。控制的變量法其難點主要是控制變量的均值解析求解，其復雜的程度是沒有QMC法高的，對偶的變量法是最簡單的，而精確度只比控制的變量法略差，和普通的QMC法相比有所改善。

對多期收入的保證價格各參數給定，各QMC法都能夠對其數值解有效階段，將顯著性的水平是 a=0.05置信區間的長度當作評價的指標，得出普通QMC法置信區間的長度是最大的，對偶的變量法以及控制的變量法稍次之，而條件QMC法是最小的，且普通的QMC法具有最差的精確度，條件QMC法具有最好的精確度。

五、結語

綜上所述，在數量金融中QMC方法得到了廣泛使用，但在QMC方法的使用中還存在諸多的難題與挑戰，常見高維和間斷情況，為了確保QMC方法能夠有效使用，就需要根據針對其存在的難題與挑戰積極進行解決方法的探索，確保其方法效果充分發揮。

參考文獻：

[1]孔云波，馮新喜，許丁友，等.基于QMC采樣的GMPHD分布式融合方法[J].系統工程與電子技術，2017，08（39）：40-46.

[2]王學禎，王辰，徐敬卿.運用“合同質量管理”模式突破質量管理瓶頸[J].質量春秋，2018（9）：27-32.

[3]韓建宇.在Variance-Gamma模型下結合QMC方法對期權定價[D].北京：清華大學，2017.

[4]張剛，黃南飛，張天騏.PQMC-NRCDSK方案的設計與性能分析[J].西安電子科技大學學報（自然科學版），2020，47（01）：1-9.

[5]劉志東，許健強.基于蒙特卡洛模擬的金融資產價格跳躍非參數檢驗方法比較研究[J].數量經濟技術經濟研究，2016，33（03）：128-145.

[6]羅鑫，張金林.基于蒙特卡羅方法的含轉股價向下修正條款的可轉債定價研究[J].金融理論與實踐，2020（10）：45-53.

（作者單位：俄羅斯圣彼得堡理工大學經濟學院）