基于GeoGebra的一道課本習題的探究

王恩普

數學是研究數量關系和空間形式的一門科學，既有著無可替代的代數表達形式，又具備著更為直觀的幾何表達形式，而我們面對一些復雜的數形關系和復雜多變的幾何位置關系時，很難抽象出其本質，難以被感官直接感知，更難被理解和深化，而信息技術，恰恰是解決這個問題的最好手段之一，它可以幫助我們探索規律啟發思路，為解決問題提供直觀，便于我們進一步解決問題，下面我們通過一道課本習題來談一談GeoGebra如何助力我們揭秘“真身”.

1 問題呈現

蘇教版選修2-1第33頁第11題：

準備一張圓形紙片，在圓內任取不同于圓心的一點F，將紙片折起，使圓周過點F（如圖1），然后將紙片展開，就得到一條折痕，（為了看清楚，可把直線，畫出來），這樣繼續折下去，得到若干折痕，觀察這些折痕圍成的輪廓，它是什么曲線？

對于這個問題，跟學生交流的時候，由于操作中的條件限制，不是反映的很清楚，畢竟這個輪廓是要在大量的直線中形成的，而不去動手，又無法在頭腦中有這樣的想象，畢竟，這是個動態的過程，如果我們連基本的輪廓都不清楚，更無法準確說明它是什么曲線了，其實這時候部分學生還認為，折痕圍成的軌跡是圖1中的線段CD的中點的軌跡，面對這些無法感知的困難，來看看GeoGebra（以下簡稱GGB）給我們帶來了什么.

2 感知結果

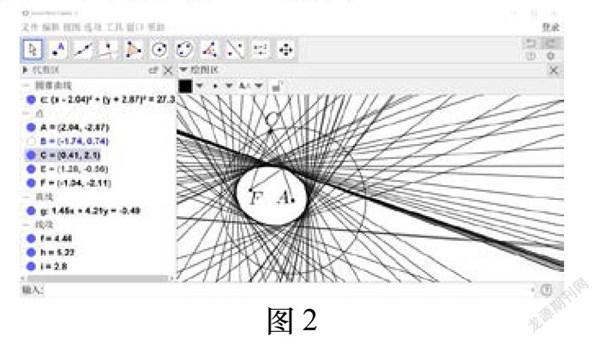
如圖2，在GGB中，我們進行下面的步驟：

步驟1首先點擊上方的工具欄中的第五個工具箱，在工具箱中選擇“圓（圓心和一點）”在繪圖區畫一個圓，在代數區顯示為圓c，默認以C為圓心，B為半徑.（也可以先用工具欄中的的第二個工具箱中的“描點”工具，在繪圖區畫出兩個點A，B，這時候在下面的指令區輸入：circle（A，B），即可得到以A為圓心，B為半徑的圓）

步驟2由于B點是控制圓的半徑的變量，我們可以選擇隱藏，只需要在代數區中點B前面的藍點點擊一下便可隱藏，然后再選用“描點”工具在圓內畫一個定點F.

步驟3這里需要說明的是，原題中的翻折過程中的直線，就是圓上動點和定點F所成線段的中垂線，所以我們在圓上再取個動點，注意圓上的動點是這樣構造的，點擊第二個工具箱的右下角的小箭頭，選擇其中的“對象上的點”，點擊繪圖區的圓周，即可得到圖中的點C.（此方法得到的點只能在圓周上移動，也可使用指令：描點（c）.即可構造圓c上的動點）

步驟4選擇第三個工具箱右下角的下拉箭頭選擇“線段”，再點擊繪圖區的點C和點F，構造線段C.再選擇第四個工具箱中的“中垂線”，在繪圖區點擊線段（F，即可作出線段C的中垂線.

步驟5在繪圖區右鍵點擊中垂線，選擇“跟蹤”，這時候我們在圓上拖動點C，就會發現多條折痕包圍成了圖2中的形狀——橢圓，

人工折紙怎么也達不到的視覺感知，GGB完成了，而且過程操作簡單，清晰直觀，也讓我們可以比較容易的下結論，真正做到了“可見”.

3 結論證明

有了上面的結果，接下來我們可以大膽的將證明的方向指向橢圓，求軌跡的問題就轉化為證明橢圓就是我們所求軌跡，且圖中的A，F分別是橢圓的兩個焦點，下面給出證明過程，

證明首先，記圓心為A，半徑為r，定點為F，C為圓上的動點，由圖3知所求軌跡上的任一點應該是橢圓與每一條中垂線的切點.設切點為Q，且設E是線段（F的中垂線上的任一點，則EC= CF，所以EF+ EA= EC+ EA，由題意知E在橢圓外（或上），所以EF+ EA≥EC+ EA，當且僅當E在橢圓上時取等號，同時當A，E，C三點共線時EC+EA最小，且此時EC+ EA=r，即EF+ EA=r，則有此時的E即為此時的切點Q，綜上有QF+ QA=r，所以Q點的軌跡為以E，A為焦點的橢圓，

點評如果我們直接去證明所求軌跡是橢圓時，是比較困難的，但是如果我們知道了是一個怎樣的橢圓時，然后結合橢圓的定義，再來說明圖中呈現的橢圓即為所求，此處便豁然開朗了.

4 嘗試探索

探索1原題中的F為圓內異于圓心的一點，如果F就在圓心，按照同樣的折法，折痕圍成一個怎樣的輪廓呢？我們來看下GGB給我們呈現的結果：

從圖4中可以清晰地發現，所求軌跡是以原來的圓心為圓心，r/2為半徑的圓，這里的證明相對簡單、清晰，此處就不再給出證明過程，由此，我們發現隨著P點位置的變化，題中的輪廓也發生了變化，而當F點的位置移到圓上的時候，由于無法圍成一個輪廓，此處不再討論，

探索2原題中的定點F如果位于圓外時，按照同樣的折法，折痕圍成一個怎樣的輪廓呢？按照題設的條件，GGB展示結果如圖5：

從圖5不難看出，結果呈現的是以F，A為焦點的雙曲線，如果是以題中的折痕形成的輪廓來看，是圓內部的上述雙曲線的一支，下面我們來證明為什么此時的雙曲線即為所求的輪廓（靠近焦點A的那一支）.

證明如圖6，首先，記圓心為A，半徑為r，定點為F，C為圓上的動點，由圖知所求軌跡上的任一點應該是雙曲線與每一條中垂線的切點，設切點為Q，且設E是線段CF中垂線上的任一點，則EC= EF，所以EF - EA= E（： - EA，由題意知E在雙曲線外（或上），所以EF - EA≤EC - EA，當且僅當E在雙曲線上時取等號，同時當A，E，C三點共線時，EC - EA最大，且此時EC - EA=r，即EF - EA=r，則此時的E即為切點Q，綜上有QF - QA=r，所以g點的軌跡為以E，A為焦點的雙曲線的一支（靠近A點）.

點評上述證明過程是類比前面證明橢圓的過程，通過中垂線的性質，構造出到兩定點的距離之差，進而利用雙曲線的定義驗證所觀察的結論，這些問題解決的前提是GGB給我們提供的直觀感知，

探索3蘇教版選修2-1第14題：

將一張長方形紙片ABCD的一只角斜折，使點D總是落在對邊AB上，然后展開紙片，得到一條折痕，（為了看清楚，可把直線，畫出來），這樣繼續下去，得到若干折痕，觀察這些折痕圍成的輪廓，它是什么曲線？

和上面一樣，我們先通過GGB來觀察折痕所圍成的輪廓，由圖7知，輪廓是以D為焦點，AB為準線的拋物線，同樣，我們來驗證結論的正確性，

如圖8，過E作線段AB的垂線，交線段ED的中垂線于點F，顯然FD= FE，則點F在以D為焦點，AB為準線的拋物線上;另一方面，在中垂線上任取異于點F的G點，記G到AB的距離為d，則有GD= GE>d，所以G點不在拋物線上，而折痕與拋物線只有一個交點，即為F.綜上可知，這些折痕圍成的輪廓是以D為焦點，AB為準線的拋物線，

點評借助于GGB，我們看到了形的特征，進而我們又在“數”上給與了驗證，讓我們從中又感受了數形結合的數學思想.

5 技術釋疑

在問題提出中提到有學生認為折痕是由線段CF的中點形成的軌跡，通過上面的圖形驗證以及結論證明，我們知道文首問題的最終軌跡并非來自于中點，那么又會產生新的疑問：隨著C點的移動，線段CF中點的軌跡是什么呢？

圖9和圖10僅僅選取了點F在圓內和圓外的兩種形式，可以看到隨著C點的移動，CF中點最終形成的軌跡都是AF的中點為圓心，初始圓半徑的一半為半徑的圓，只是F點的位置決定了圓的位置，這里的證明比較容易，只需要取AF的中點和E相連，再連接A（，這里就不再進行證明，

點評在這樣的探索中我們不僅真正地了解了折痕圍成的輪廓，還認識了中點的軌跡，讓我們很清晰地辨識出它們之間的差異.

6 結束語

當然我們還可以借助于GGB進行更多的探索，如果把文中的圓換成橢圓，或者換成雙曲線，或者換成拋物線，折痕又是什么呢？在數學的學習過程中，我們會遇到許許多多的“不可見”，它們無法被感知，無法被呈現，而GGB正是發揮了它們的可視化優勢，揭秘“真身”，揭示本質，突破數學因高度抽象概括的特性而帶來的“難以意會、無法言傳”之障礙，為我們的數學學習以及探索提供了極大可能，