高動態GPS 抗干擾算法仿真研究*

陳嘉鑫，黎柏春

（中國民航大學 航空工程學院，天津 300300）

0 引言

GPS（global positioning system）系統作為目前世界上應用最廣泛的衛星導航系統，在國家經濟建設和國防安全方面有著非常重要的地位。在高動態的環境下，GPS 接收機載體的速度和加速度會有較大的變化范圍，再加上會有其他的干擾源會散發干擾信號，使得GPS 接收機對衛星信號的捕捉、跟蹤和定位難度會進一步增大。因此，對于高動態環境下GPS性能研究仍然有非常大的研究空缺，需要不斷完善。

目前，已有多種抗干擾技術，這些技術包含時域處理法、頻域處理法、時頻域處理法、空域處理法和空時域處理法等［1-3］。現階段，美國在研究第3 代GPS，將抗干擾作為核心問題，對其進行了大量的研究和總結，許多研究成果都直接面向實際應用。在我國，抗干擾難題也成為國內許多高校和研究所的研究方向。例如西安電子科技大學提出的在微分約束下空域最小功率遞推法［4-5］，中國民航大學的微分約束最小功率抗干擾算法，國防科大的GPS 空時抗干擾的仿真和研究成果等［6-10］。但是國內的抗干擾算法研究還不是太深入，許多成果還是基于國外提出方法的跟蹤、改進和實現。

1 高動態環境下陣列接收信號模型

1.1 高動態環境的定義

早在1988 年，美國宇航局噴氣推進實驗室在一份關于高動態GPS 信號跟蹤技術的報告中就明確給出了高動態的2 種定義。第1 種是在1 s 內有70 g的加速度斜升，也就是用70g/s 的加加速度持續1 s；第2 種比第1 種情況還要更劇烈，是0.5 s 內有50g的加速度斜升，也就是用100g/s 的加加速度持續0.5 s，而且50g/s 的加速度持續2 s，最后在0.5 s 產生50g/s 的加速度斜降。

1.2 高動態下陣列接收信號模型

設置M元等距離線陣，各陣元之間距離，其中λ為入射信號的載波波長，另設信號入射方向方位角為φ，是與陣列法線方向夾角所形成的方位角，φ∈[-π/2，π/2]。設最左側的陣元為原點，可以推導出信號的入射導向矢量為

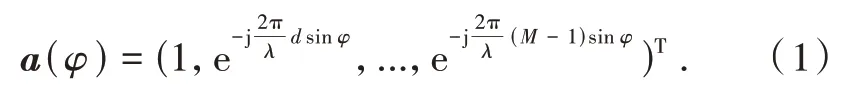
GPS 接收機接收到的信號中包含許多顆衛星信號，還有干擾信號和噪聲，各信號及噪聲之間相互獨立。因為衛星離地球地面距離較遠，可近似認為相對于穩定的接收機，接收到的衛星信號來向不變，而干擾相對于接收機距離較近，認為干擾信號來向會快速變化。設有W個衛星信號、Z個干擾信號，陣列接收到的信號模型表示為

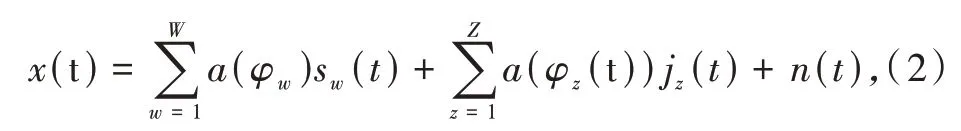
式中：sw(t)表示第w個衛星信號(w= 1，2，...，W)；φw表示衛星信號的來向；jz(t)表示第z個干擾信號；φz表示干擾信號的來向；n(t)表示接收機熱噪聲矢量，一般是均值為0，方差為σ2n的高斯白噪聲矢量。因為衛星距離地球遠，信號到達接收機會損失很多能量，其電平會遠低于噪聲電平，所以可認為陣列接受信號的協方差矩陣主要由干擾信號與噪聲信號決定，設協方差矩陣R為

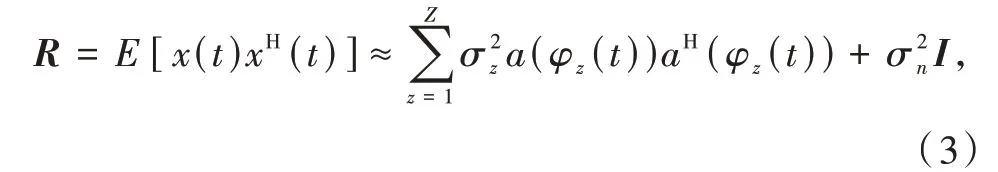
式中：σ2z為第z個干擾信號的功率；σ2n為噪聲功率；I為單位矩陣。因為自適應處理要求信號是穩定的，但式（3）中的協方差矩陣是不斷變化的，所以只有少數可以用來估計自適應處理的協方差矩陣，式（3）轉變為

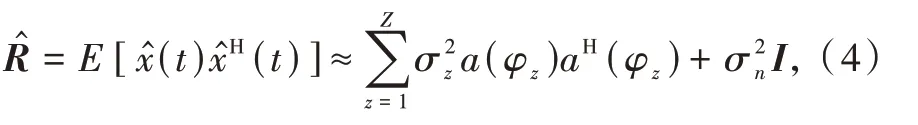
式中：φz表示此刻的干擾來向；?(t)表示此刻快拍數很少的采樣數據，采樣的協方差矩陣的第m行第n列元素則可以表示為

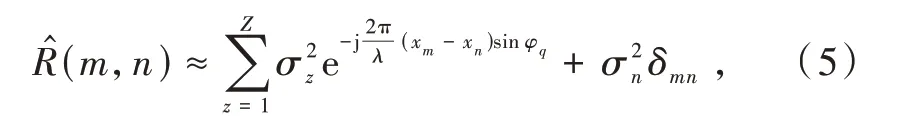
式中：δmn為Kroneckerδ函數，即當m=n時，δmn=1；當m≠n時，δmn=0。

2 Mailloux 算法原理及仿真

2.1 Mailloux 算法原理［11］

設M元等距離線陣，相鄰陣元之間距離為d，接受了P個遠距離的窄帶信號，入射角設為φP，則陣列接受的快拍數據表示為

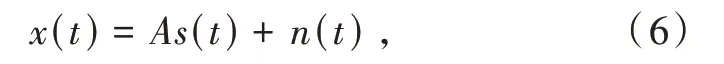
式中：x(t)=(x1(t)，x2(t)，...xM(t))T，x(t)為M× 1 維陣列數據向量；A為陣列流行矩陣，A=(a(φ1)，a(φ2)，...，a(φp))，矩陣中a(φp)表示第p個信號 源 的 導 向 矢 量表示為信號復包絡向量，sP(t)是第p個信號源的復包絡。n(t)=(n1(t)，n2(t)，...nM(t))T為M×1維陣列噪聲向量。陣列的協方差矩陣定義為

式中：Rs=E[s(t)sH(t)]為信號的協方差矩陣；Ι為M維度單位矩陣；σ2n為噪聲的功率。Mailloux 方法是假設在接收機接受的干擾信號源附近，存在K個相等強度的虛擬干擾，并按照一定的空間間隔排列，用來構建一個新的協方差矩陣Rˉ。用新的協方差矩陣進行自適應處理時相比于原協方差矩陣，會在接受的干擾方位附近產生較寬的零陷。新的協方差矩陣可以表示為

式中：R為沒加虛擬干擾的接收信號的噪聲協方差矩陣；符號⊙表示Hadamard 積；T為擴展矩陣［6］，表達式為

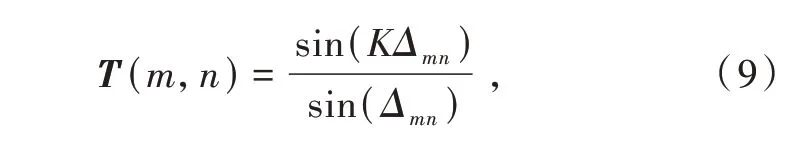
式 中：T(m，n) 表 示 矩 陣T的 第m行 第n列；Δmn=π(xm-xn)β/λ，xm和xn分別為等距線陣上第m，n個陣元的位置，β=B/(K- 1)，表示虛擬干擾源之間的距離，一般很小，B為虛擬的角度寬度擬干擾源。

根據式（9）可知，如果等距線陣用Mailloux 方法，不需要知道干擾信號的來向。當m=n時，擴展矩陣T的元素T(m，n) =K。新的協方差矩陣會使原協方差矩陣的噪聲項功率增強K倍。

2.2 MVDR 算法仿真

仿真時，為了顯示該方法形成的零陷較寬，考慮需要有對照方，所以選擇MVDR（minimum variance distortionless response）算法作為常規方法，即對照方。設置陣元數為32 的等距線陣，快拍數為100，工作頻率為3 × 109Hz，波長為光速除以工作頻率，陣元間隔為波長的一半，干燥比為40 dB，信噪比為0 dB。因為高斯白噪聲信號的功率是單位1，所以可以通過干燥比來反推得出干擾信號，通過信噪比來反推得出期望信號。設置2個互相獨立的干擾信號入射至陣列接收模型，入射角度分別為-30°和30°，干擾頻率 分 別 設 為5 × 109Hz 和6 × 109Hz，帶 寬 為0.3 GHz，而期望信號的入射角在0°方向。將期望信號、干擾信號進行空域處理，將處理后的期望信號、干擾信號，和用randn 函數產生的噪聲信號疊加，即可得陣列接收信號x(t)，通過x(t)根據式（3）得出協方差矩陣R。計算最優權值，進行空間角度掃描和計算空間導向矢量，最后畫出方向圖，得到MVDR 算法的方向圖，如圖1 所示。從圖1 中可以明顯看出MVDR 算法在2 處干擾方向上形成的零陷很窄。

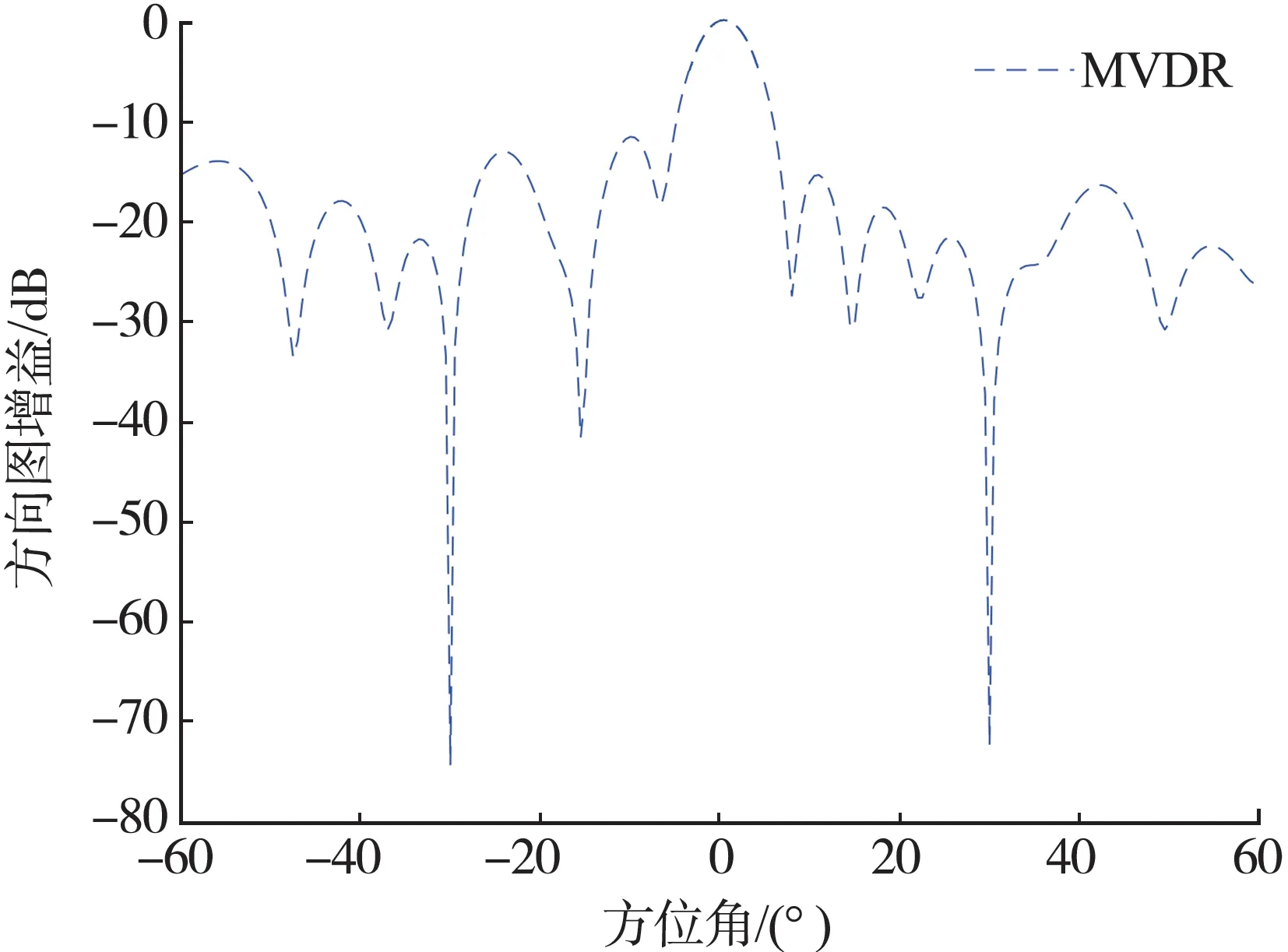
圖1 MVDR 算法的方向圖仿真結果Fig.1 Simulation results of MVDR algorithm

2.3 Mailloux 算法仿真

Mailloux 方法則是需要在原協方差矩陣R上乘上擴展矩陣T，設2 個干擾信號有方向上的擾動，擾動的角度最大范圍為6°，即B= 6°，加入7 個虛擬干擾源。根據式（9）計算可得出擴展矩陣T，根據式（8）算出新協方差矩陣Rˉ。通過新的協方差矩陣來算最優權值，進行空間角度掃描和計算空間導向矢量，最后畫出方向圖，得到Mailloux 算法與MVDR 算法的方向圖對比，如圖2 所示。從圖2 對比來看，Mailloux 方法能夠明顯地加寬干擾方向上形成的零陷。

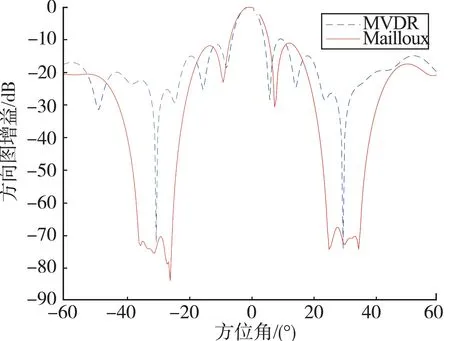
圖2 Mailloux 算法的方向圖仿真結果Fig.2 Direction diagram simulation results of Mailloux algorithm

2.4 高動態下算法對比仿真

2.4.1 加入1 顆衛星信號仿真

以上是沒有加入GPS 信號的仿真，本文研究GPS 抗干擾，所以以下是加入了GPS 信號的仿真。GPS 衛星信號可以用2 種方法產生，第1 種是直接調用已生成的GPS 數據文件，第2 種是用GPS 數據模擬器產生所需要的GPS 數據文件。本文采用的是第1 種方法，調用GPS 衛星信號產生程序，該程序調用已生成的GPS 衛星信號數據文件，先調用了1 顆衛星信號，衛星信號編號為1，讀取0.1 s 的衛星信號數據，設置采樣率為5 714 000 Hz，所以衛星信號數據為1 × 5 714 00 維矩陣。為保證程序能夠運行，所以將快拍數也改為5 714 00。將產生的GPS 衛星信號矩陣替代原仿真程序中的期望信號。陣列接收信號模型重新設置為7 元陣列等距線陣，保留一個干擾信號，干擾來向設為-30°，干擾信號和噪聲信號矩陣改變維度，其他如工作頻率和波長都不變。

因為衛星軌道高度在20 000 km 以上，高動態GPS 接收機距離衛星很遠，所以在短時間內，近似認為接收機接收到的GPS 衛星信號的來向不變，也就是φw不變，仿真中設為30°。為了體現高動態，認為干擾信號距離接收機較近，所以認為干擾信號的波達方向會逐漸變化，但變化不大。仿真中為了直觀方便，設置干擾信號的前N/2 個數據的波達方向為-30°，后N/2 個數據的波達方向為-32°。利用干擾信號的前N/2 個數據求解陣列加權向量，得到高動態下Mailloux 算法的方向圖，如圖3 所示。

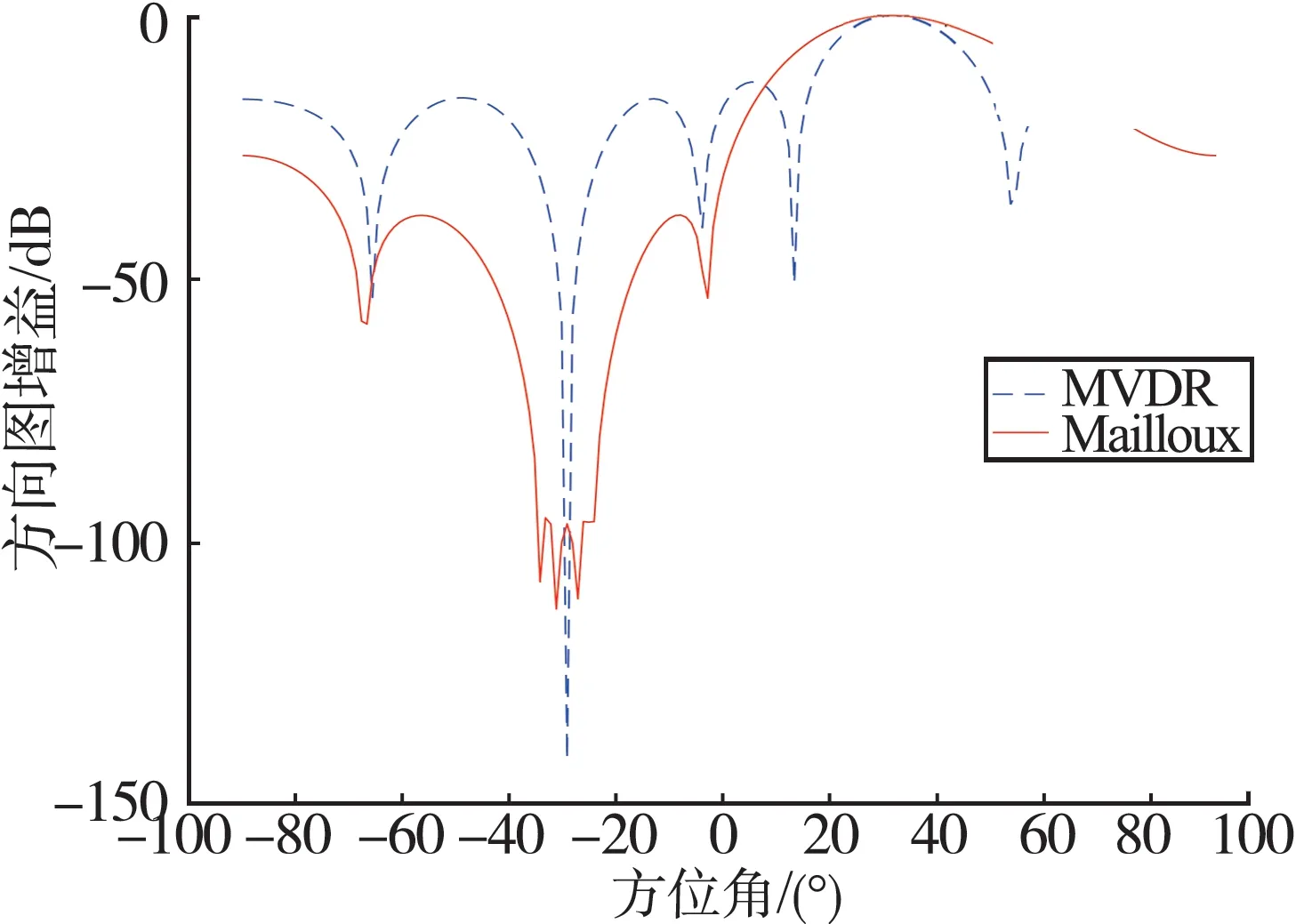
圖3 1 顆衛星的Mailloux 算法方向圖仿真結果Fig.3 Direction diagram of one satellite based on Mailloux algorithm

從圖3 中可看出，零陷明顯加寬。

新建函數：

式中：WH為利用干擾信號的前N/2 個數據求解陣列加權向量；X為后N/2 個樣本數據。

將新建函數作為輸入參數帶入捕獲程序進行捕獲。先計算每個C/A 碼包含多少采樣點，取相鄰的2 個信號，信號長度為1 ms，去直流，計算采樣時間間隔，計算1 ms 信號內的載波相位點，計算頻率捕獲的個數，產生一顆衛星的載波偏移初始向量，初始化32 顆衛星的載波頻率，對已產生的當前通道的C/A 碼做離散傅里葉變換，掃描頻點，找出最大的值及其對應的頻點，確認最大值對應的相位，獲取與最大峰超過1 個碼片的次最大峰，求與最大峰距離為1 個碼片的區域邊界，確定尋找次最大峰的搜索區域，保存各通道峰峰比值，判決，如果比值比預設閾值大，則表示能接收到該衛星信號。圖4 為MVDR 算法1 號 衛星信號捕獲圖，圖5 為Mailloux 算法1 號衛星信號捕獲圖。

圖4 MVDR 算法1 號衛星信號捕獲圖Fig.4 Signal acquisition diagram of satellite No.1 base on MVDR algorithm

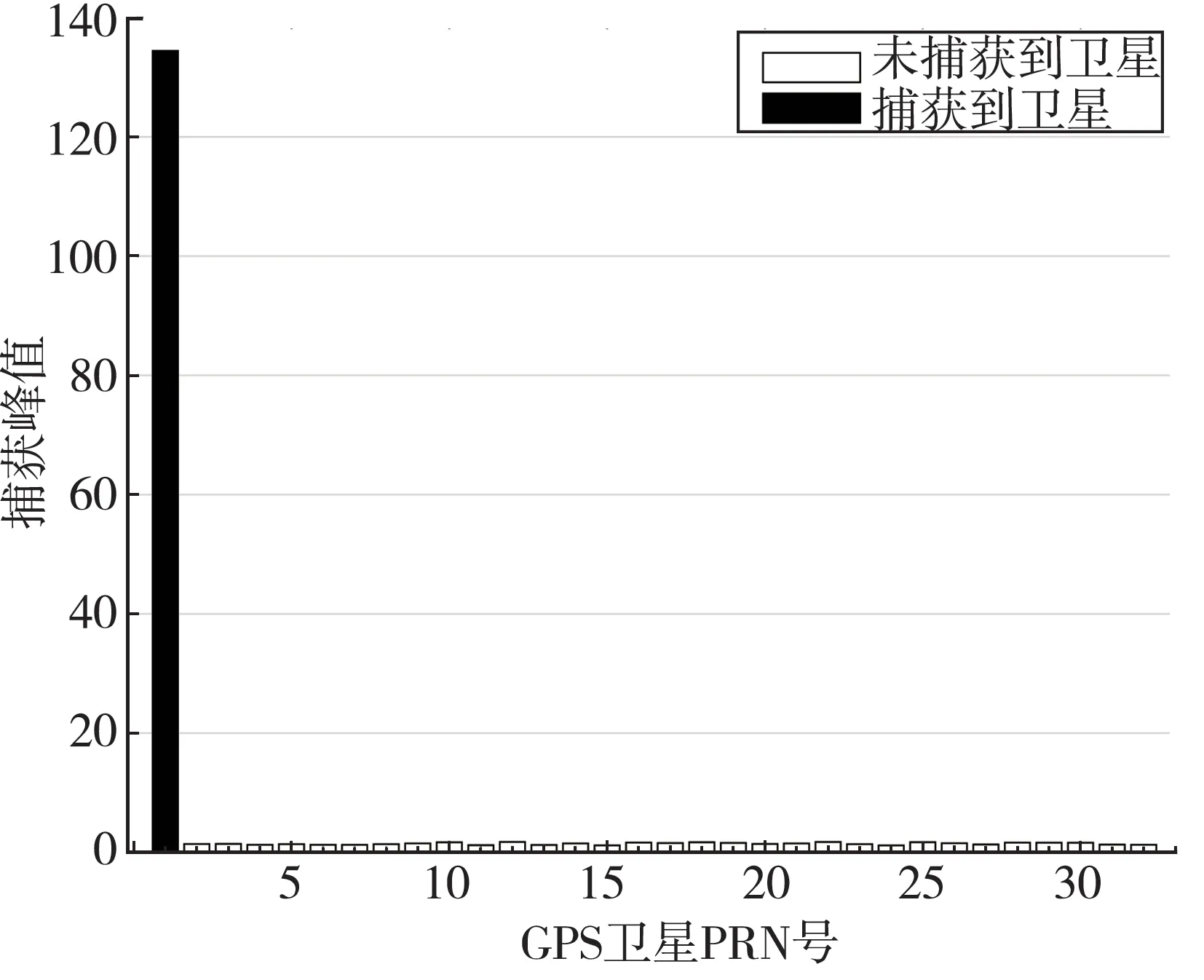
圖5 Mailloux 算法1 號衛星信號捕獲圖Fig.5 Signal acquisition diagram of satellite No.1 based on Mailloux algorithm

2.4.2 加入4 顆衛星信號仿真

為驗證算法可行度，加入多個衛星信號。調用4 顆衛星信號，分別是1，2，3，20 號衛星。圖6 是加4顆衛星的Mailloux 算法的方向圖，圖7 是MVDR 算法4 顆衛星信號捕獲圖，圖8 是Mailloux 算法4 顆衛星信號捕獲圖。當加入多顆衛星后，如果捕獲圖8中沒有出現已加入的衛星序號，只需要將捕獲門限值提高一點即可。從圖7，8 的對比來看，Mailloux 算法在高動態條件下能夠捕獲衛星信號。

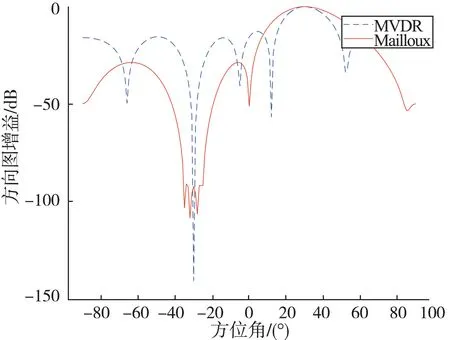
圖6 4 顆衛星的Mailloux 算法的方向圖Fig.6 Direction diagram of four satellites based on Mailloux algorithm

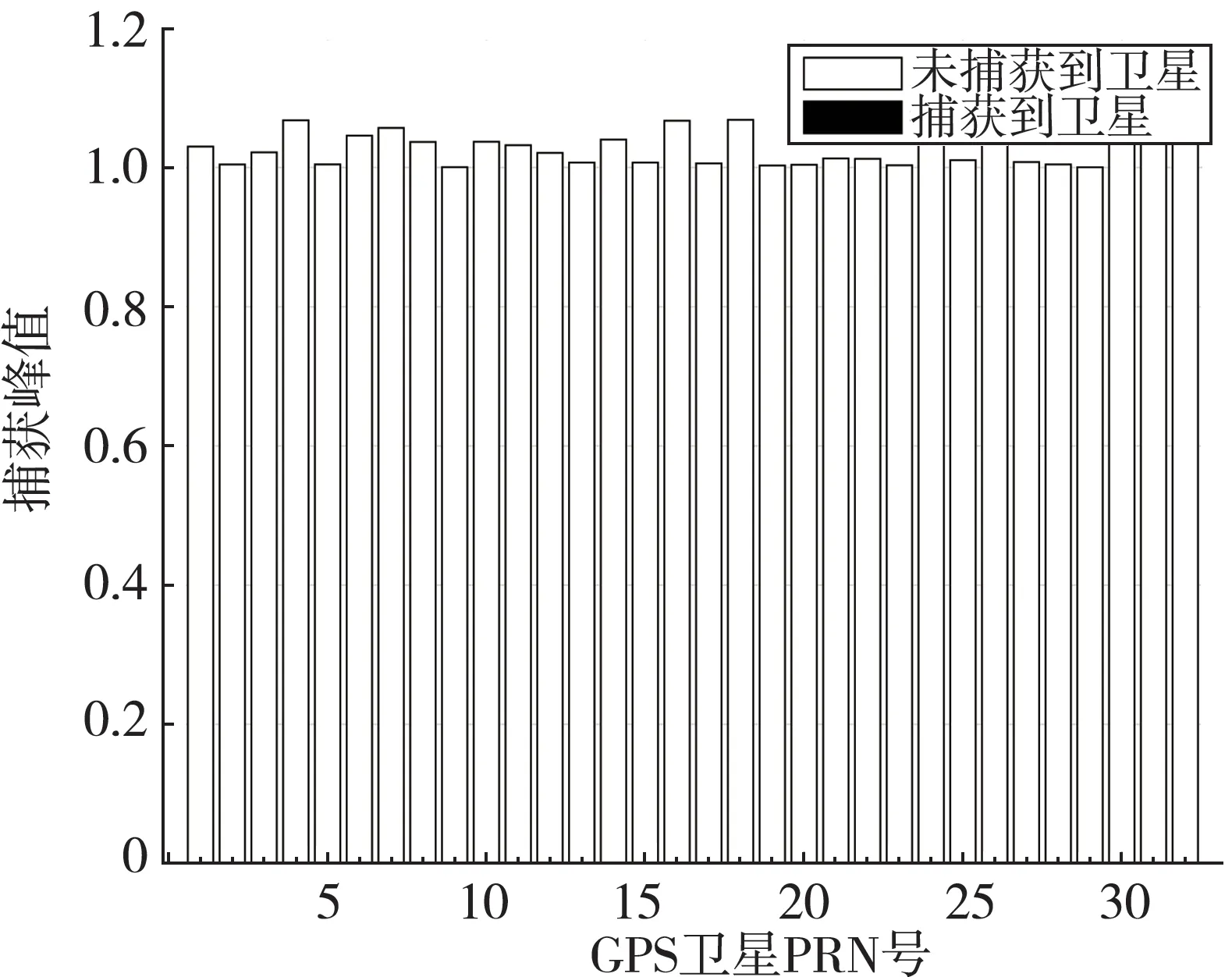
圖7 MVDR 算法4 顆衛星信號捕獲圖Fig.7 Signal acquisition diagram of four satellites based on MVDR algorithm

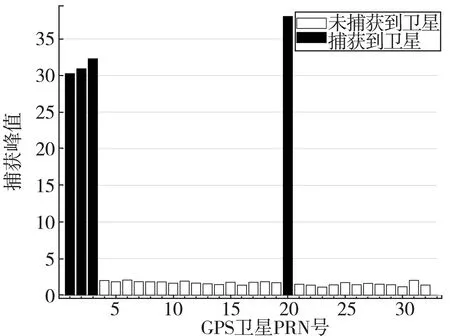
圖8 Mailloux 算法4 顆衛星信號捕獲圖Fig.8 Signal acquisition diagram of four satellites based on Mailloux algorithm

3 Zatman 算法原理及仿真

3.1 Zatman 算 法原理［12-14］

Zatman 方法是假設接收機接受的窄帶干擾信號具有虛擬帶寬Bw，而且在整條帶寬內有平坦的功率譜，用來構建一個新的協方差矩陣Rˉ，用新的協方差矩陣進行自適應處理時相比于原協方差矩陣，會在接受的干擾方位附近產生較寬的零陷。新的協方差矩陣可以表示為

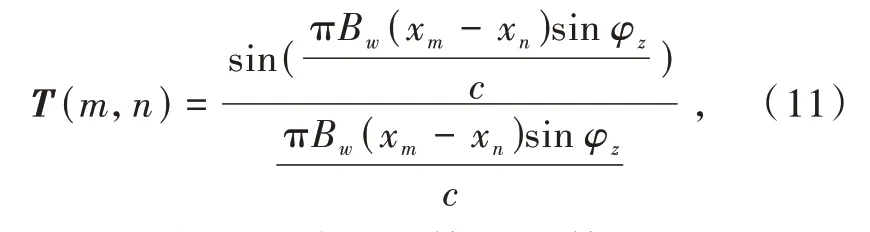
式中：T(m，n)表示矩陣T的第m行第n列；xm和xn分別為等距線陣上第m和n個陣元的位置；φz表示第z個干擾信號的來向；c為光速。

由式（11）可知，Zatman方法需要知道干擾信號的來向。當m=n時，擴展矩陣T的元素T(m，n) = 1，不會改變原協方差矩陣R中的噪聲項功率。

3.2 Zatman 算法仿真

對照方依舊選擇MVDR 算法。先不加衛星信號，使用期望信號。陣元數為32 的等距線陣，快拍數為100，使用2 個獨立的干擾信號。工作頻率為3 ×109Hz，波長等于光速除以工作頻率，陣元間隔為波長的一半，干燥比為40 dB，信噪比為0 dB，設高斯白噪聲的功率為1。通過干燥比反推得到干擾信號，通過信噪比反推得到期望信號。將各信號疊加得到x(t)，剩余的操作與第3 節中MVDR 算法仿真中的操作一致。MVDR 算法得到的方向圖如圖1 所示。

Zatman 算法是在MVDR 算法的基礎矩陣上再乘上一個擴展矩陣T。假設干擾信號的頻帶擴展寬度為0.3 GHz，即Bw= 0.3 GHz。根據式（11）得到擴展矩陣，根據式（8）算出新協方差矩陣Rˉ。通過新的協方差矩陣來算最優權值，進行空間角度掃描和計算空間導向矢量，最后畫出方向圖，得到Zatman 算法與MVDR 算法的方向圖對比，如圖9 所示。

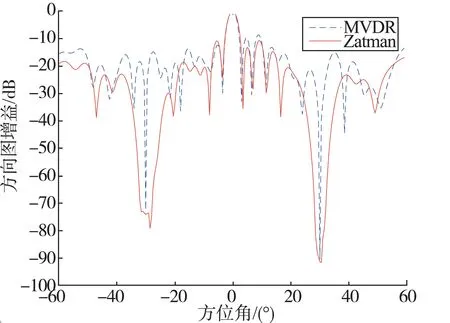
圖9 Zatman 算法的方向圖Fig.9 Direction diagram of Zatman algorithm

3.3 高動態下算法對比仿真

3.3.1 加入1 顆衛星信號仿真

以上是沒有加衛星信號的仿真，以下是加入衛星信號的仿真。還是用第1 種方法直接調用已生成的GPS 數據文件。先調用1 號衛星信號，讀取參數與第3 節里一致。

為保證程序能夠運行，將快拍數也改為571 400。將產生的1 號衛星信號矩陣替代原仿真程序中的期望信號。設置7 元陣列等距線陣，保留一個干擾信號，干擾來向設為-30°。為了體現高動態，也將設置干擾信號的前N/2 個數據的波達方向為-30°，后N/2個數據的波達方向為-32°。用前N/2 個數據求解陣列加權向量，得到的加權向量處理后N/2 個數據，得到加寬的方向圖，如圖10 所示。從圖10 中可看出，零陷加寬。

圖10 1 號衛星的Zatman 算法的方向圖Fig.10 Direction diagram of one satellite based on Zatman algorithm

根據式（10）得到新建函數，將新建函數送入捕獲程序中捕獲衛星信號。捕獲程序流程與2.3中所寫一致。MVDR 算法1 號衛星信號捕獲圖如圖4 所示，圖11 為Zatman 算法1 號衛星信號捕獲圖。從圖11 中可知，Zatman 算法在高動態條件下可以捕獲到1 號衛星。

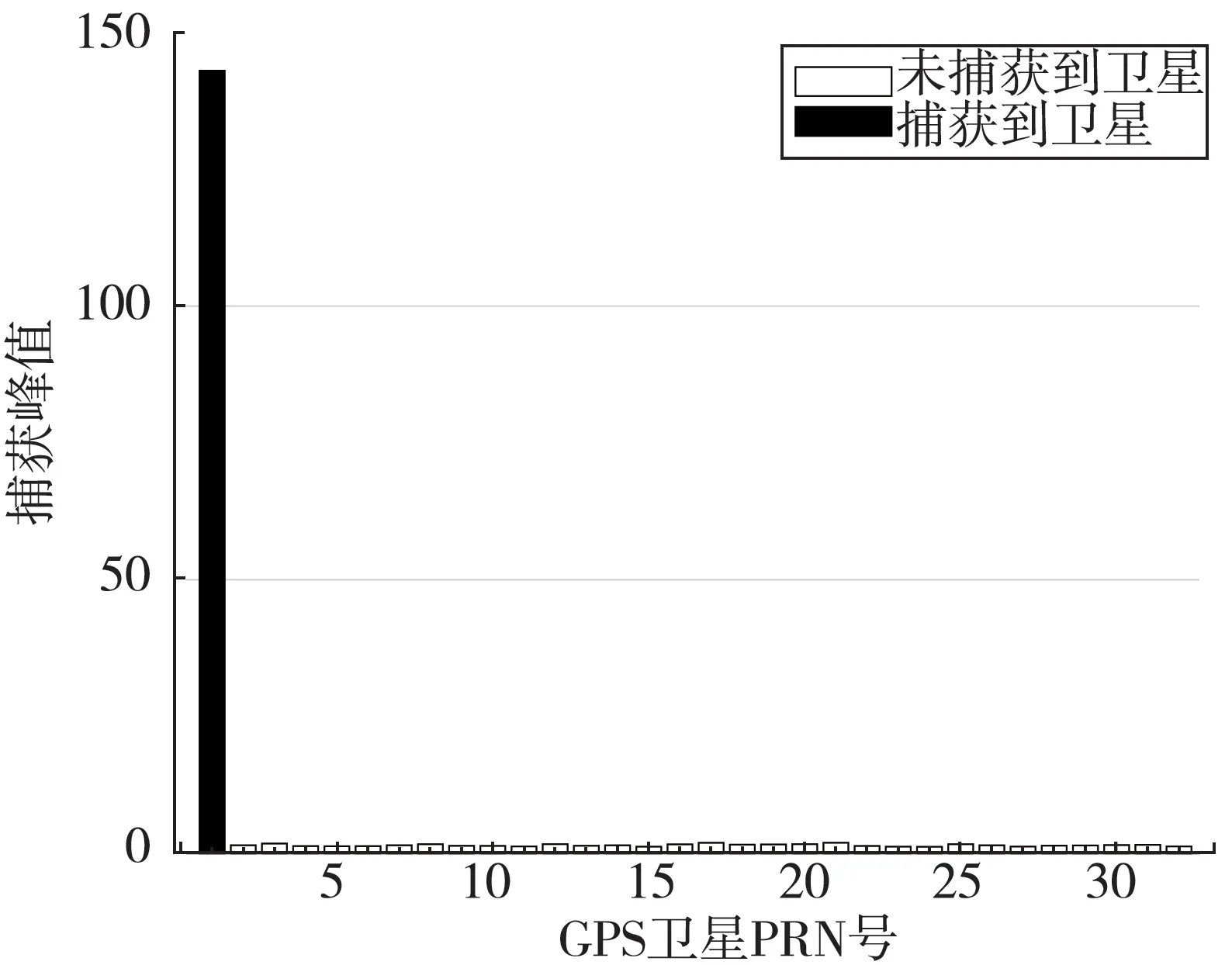
圖11 Zatman 算法1 號衛星信號捕獲圖Fig.11 Signal acquisition diagram of satellite No.1 based on Zatman algorithm

3.3.2 加入4 顆衛星信號仿真

為驗證算法有效性，加入多個衛星信號進行仿真。調用4 顆衛星信號，分別是1，2，3，20 號衛星。圖12 為加4 顆衛星的Zatman 算法的方向圖，MVDR算法4 顆衛星信號捕獲圖如圖7 所示，圖13 為Zatman算法4 顆衛星信號捕獲圖。當加入多顆衛星后，捕獲圖也出現了Mailloux 算法類似的問題，同樣只需要將捕獲門限值提高一點即可。從圖7，13 的對比來看，Zatman 算法在高動態下能夠捕獲衛星信號。

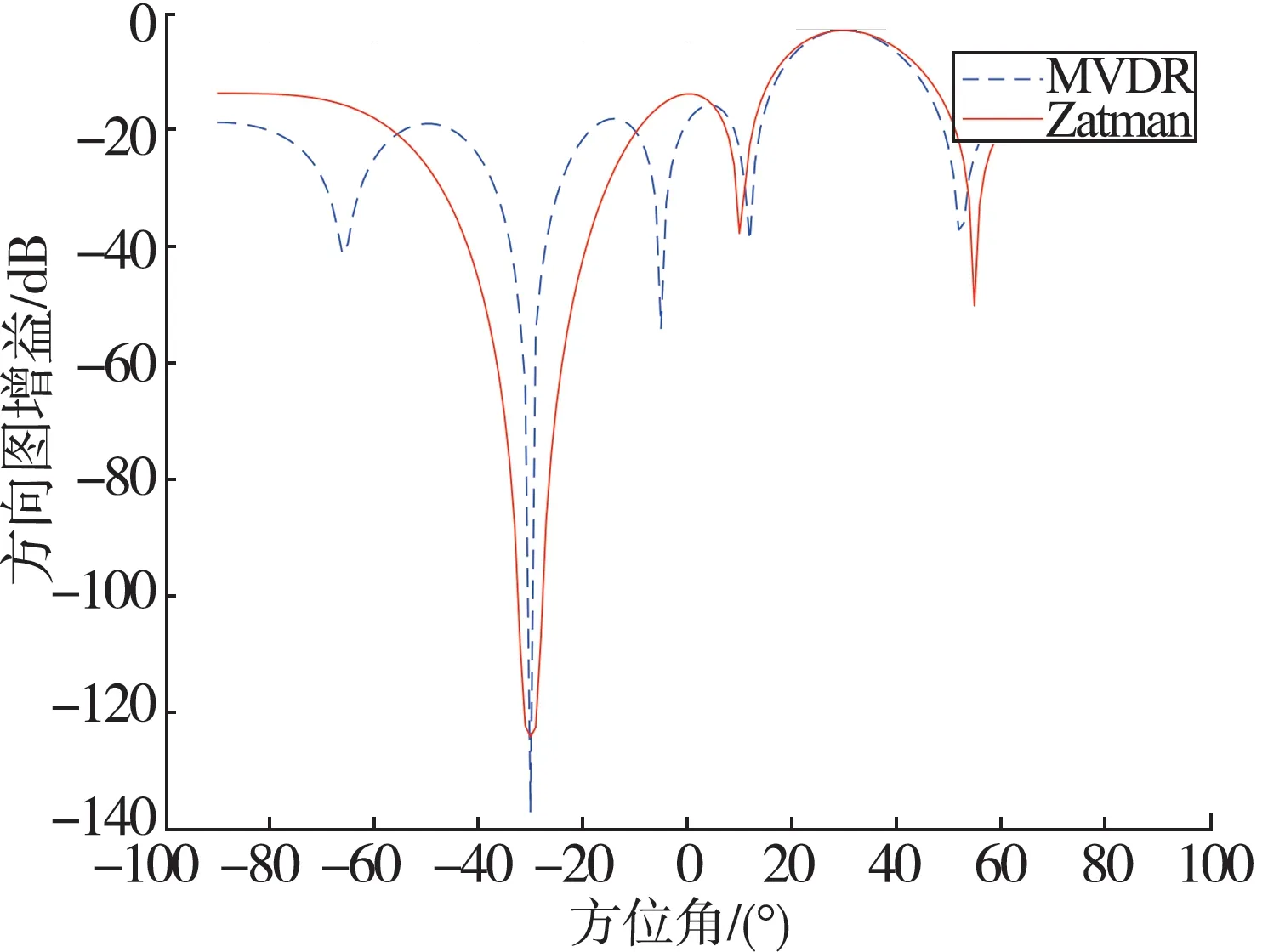
圖12 4 顆衛星的Zatman 算法的方向圖Fig.12 Direction diagram of four satellites based on Zatman algorithm

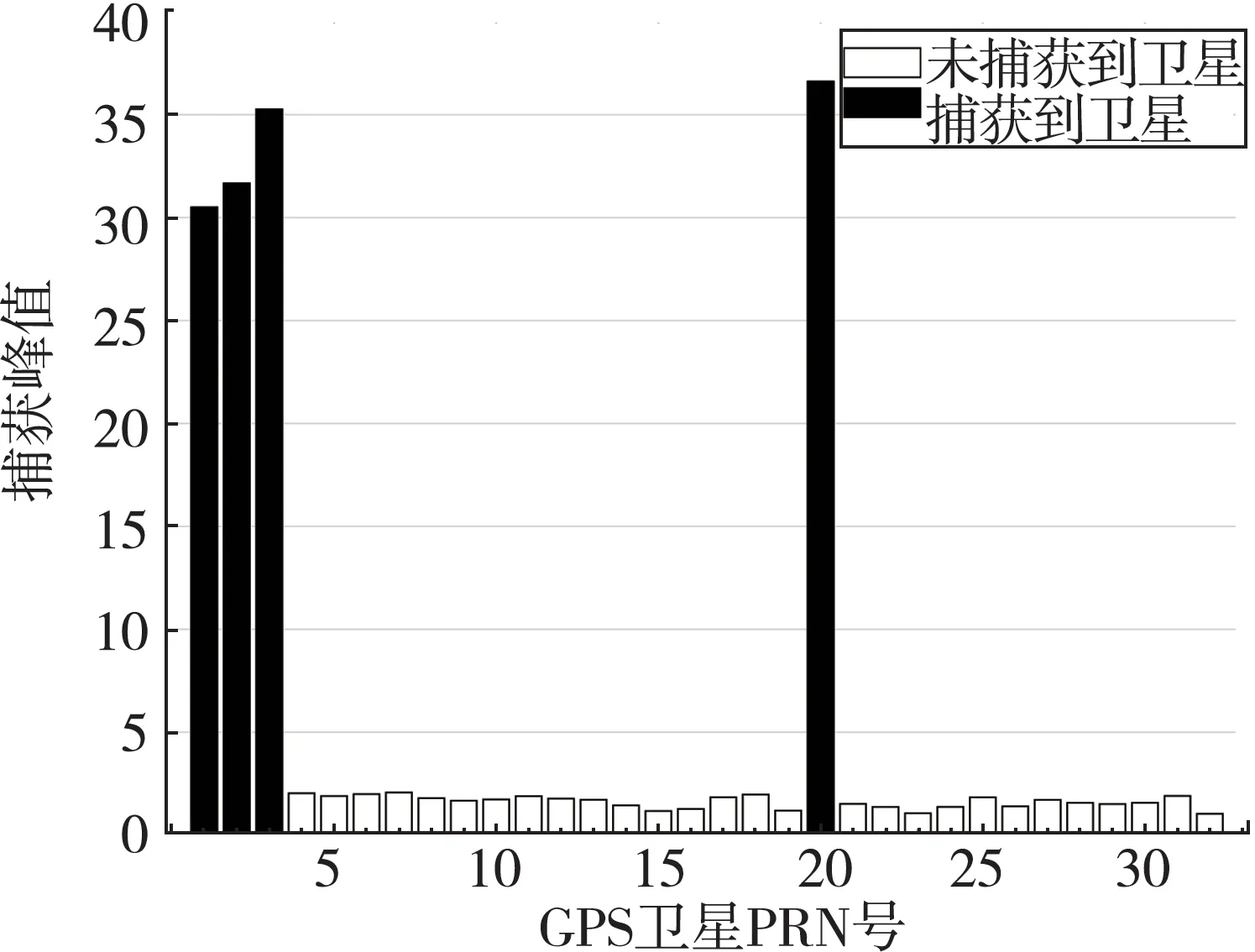
圖13 Zatman 算法4 顆衛星信號捕獲圖Fig.13 Signal acquisition diagram of four satellites based on Zatman algorithm

4 Mailloux 算 法 和Zatman 算 法 的 優缺點對比分析

根據2 種算法的推導和仿真結果的對比可得，Mailloux 算法運算量適中，在線陣模型中不需要估計干擾來向，可以直接得到擴展矩陣，但在面陣模型中，該算法需提前給出預估得干擾信號來向。此外還有一個缺點，用T計算Rˉ時，協方差矩陣的噪聲項功率會增強K倍。該算法在方向圖干擾來向上形成的零陷比Zatman 算法較寬，比MVDR 算法寬很多。

Zatman 算法運算量不大，對于干擾噪聲的協方差矩陣的功率沒有增強，但無法保證角度的取值，不能進行角度的擴展，因此該算法不可應用于面陣，只可用于線陣。該算法在方向圖干擾來向上形成的零陷比MVDR 算法寬，但相比Mailloux 算法要窄一些。

通過2 種算法得對比可知，Zatman 算法不能用在圓陣以及任意陣模型下，利用Mailloux 算法需要預估干擾的來向信息。但是，如果干擾方向隨時間快速變化，難以得到干擾方向的來向信息，Mailloux算法便不能解決問題，與此同時也會增加很大的計算量。

5 結束語

本文首先研究了當陣列為等距線陣時接收信號模型。根據信號入射的導向矢量和信號中不同組成部分，得到陣列接收信號模型。并由信號模型求得協方差矩陣，來表示各個維度信號之間的相關性。在Matlab 上搭建了陣列接收信號模型。之后對Mailloux 算法和Zatman 算法原理進行了研究分析。仿真時在陣列接收信號模型的基礎上，通過虛加干擾源和擴展頻帶來獲得擴展矩陣，從而得到新的協方差矩陣。為更直觀驗證算法的有效性，選擇MVDR 算法作為對照。最后為體現高動態的特點，仿真時改變干擾信號數據后半部分的來向。用前半部分數據計算新的協方差矩陣，得到的矩陣處理后半部分數據。

通過仿真驗證可知，在高動態條件下，當陣元是等距線陣時，Mailloux 算法不需要知道干擾的來向信息，但Zatman 算法需要知道干擾的來向。相較于MVDR 算法，Mailloux 算法和Zatman 算法都能在方向圖干擾來向上形成較寬的零陷，能夠有效抑制掉干擾信號。根據需要，將3 種算法形成的新建函數送入捕獲程序后，MVDR 算法不能捕獲到衛星信號，而Mailloux 算法和Zatman 算法能捕獲到衛星信號。

本文只驗證了陣列接收信號模型是在等距線陣時算法的有效性。由于在飛機、導彈等一系列高速運動的載體上，圓陣列的應用比較廣泛，后續將驗證圓陣列和其他任意形模型下，Mailloux 算法和Zatman 算法在高動態條件下的抗干擾有效性。